平成15年度の大学入試センター試験(1/18・19)も無事終わった。数学だけをみると、今
年度の問題としては、全体として例年並であるが、一部計算量の多い問題、極端に易しい問
題、平面幾何の知識も背景として問われる問題など、ある程度の実力を問う良問ぞろいのよ
うである。その中で、数学Ⅰ・A の第4問(平面幾何)は、とても興味深い。
2等辺三角形ABC (AB=AC)において、AC に接する傍接円の中心を O とする。この傍
接円と辺 BC の延長との接点を E 、A から辺 BC に下ろした垂線の足を D とするとき、四
角形 ADEO は長方形であることを示せ。(実際の問題の趣旨を生かす形で、問題を修正)
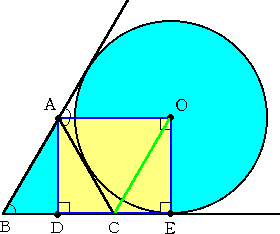
長方形になることを示すのは、容易である。
実際に、
AD と OE は、平行 (D が垂線の足、E が接点であることから)
AO と DE は、平行 (同位角相等から)
よって、四角形 ADEO は平行四辺形
ところで、∠ADE=∠R より、四角形 ADEO は長方形となる。
一般に、三角形の傍接円は、次のように作図される。
1つの内角及び2つの外角それぞれの角の2等分線の交点として傍接円の中心を、まず作
図し、さらに、中心から辺 BC の延長に垂線の足を下ろし、その垂線の長さを半径として、傍
接円を描く。
以上の作業の煩雑さから、その結果できる四角形ADEO の形状が何であるかは、今まで、
あまり考えたことはなかった。2等辺三角形という特殊な条件のもとで、四角形 ADEO が長
方形になるという事実は、とても面白い。
