角の二等分線の長さ 
もうすぐ、今年も大学入試センター試験の日を迎える。いたずらな難問・奇問を排除し、
適正な高校教育を守るという趣旨で始まったこの試験も、共通一次試験(1979〜1989)か
ら数えて、既に四半世紀を過ぎようとしている。2020年度でその使命を終え、2021年度
からは「大学入学共通テスト」が始まる。
確かに、難問・奇問は確実に減ったが、逆に問題がスタンダードすぎて、ある程度の訓
練を積めば誰でもが高得点を得られるような感じさえ受ける。
受験生当人にとっては、それはそれで好ましいことかもしれないが、入試問題から高校
教育を見つめる立場の人達にとっては、とても歯がゆい現実なのだろうと思う。
「数学は一つ」だと思うのだが、なぜかしらこの時期、書店では「センター試験対策問題
集」とかが山積みされていて、よく売れているらしい。また、高校では、センター試験対策
と称して、授業や補講などが組まれることは、もう常態化している。
センター試験は原則、選択肢のある穴埋め問題なので、論理性を無視しても、いかに
手早く正解を得るかが重要で、その対策の経験の有無が結果に大きく影響を与えると言
われる。
共通一次試験発足当時の趣旨とは別な方向に社会全体が動いているようで、なぜか
不気味だ。
このような現状を踏まえて、センター試験の問題を作っておられる方々も、作問にいろ
いろ工夫を重ね、なるだけ記述式と同様な効果が期待できるようにと努力しておられる
姿が問題からひしひしと伝わってくる。
そういうわけで、毎年この時期、センター試験の問題に触れるのが楽しみになっている。
角の二等分線に関する公式が、初めて共通一次試験に登場したのは、多分平成元年
だろうと思う。(手持ちの資料に欠損があって、詳細は不明)
今では、どこの教科書にも大抵書いてある公式だが、当時はとても新鮮に映った。
角の二等分線の公式 (→ 一般化:「角の2等分線」)
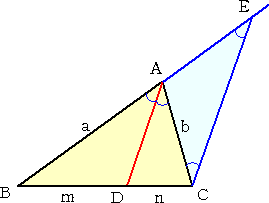 |
△ABC において、ADは∠Aの二等分線である。
このとき、 AB : AC = BD : DC
が成り立つ。
(∠Aの外角の二等分線についても同様の公式が
成り立つ。→ こちらを参照)) |
(証明) BAの延長線上に、AE=AC となる点Eをとる。
△ACEは二等辺三角形なので、 ∠ACE=∠AEC
三角形の外角の性質から、 ∠ACE+∠AEC=∠BAC
ADは∠Aの二等分線なので、 ∠BAC=2∠BAD
よって、 2∠AEC=2∠BAD より、 ∠AEC=∠BAD
したがって、同位角が相等しいので、AD と EC は平行となる。
ゆえに、平行線の公理から、 AB : AE = BD : BC
AE=AC なので、 AB : AC = BD : BC (証終)
この公式を用いる基本的な出題の仕方としては、AB、ACの長さと∠Aの大きさを与え
て、二等分線の長さADを求めさせることが多い。(もちろん、三角形の面積の公式を用
いて、ADの長さが求められる場合もある。)
最近、BD、DCの長さが分かっている場合に、ADの長さを求める公式があることを知
った。いままで経験した問題で、最初から、BD、DCの長さを与えるという問題はないが、
公式として美しい形をしているので、裏技として取り上げたいと思う。
角の二等分線の長さの公式
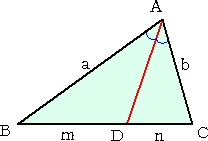 |
△ABC において、ADは∠Aの二等分線である。
このとき、 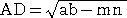 が成り立つ。 が成り立つ。
|
(証明) △ABC において、余弦定理から、
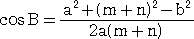
△ABD において、余弦定理から、AD2=a2+m2−2amcosB
上式を代入して、整理すると、
(m+n)AD2=(a2+m2)(m+n)−m(a2+(m+n)2−b2)
から、(m+n)AD2=na2+mb2−mn(m+n)
ここで、角の二等分線の公式から、 a : b = m : n なので、 na=mb
よって、(m+n)AD2=mab+nab−mn(m+n)=ab(m+n)−mn(m+n)
したがって、 AD2=ab−mn となり、明らか。 (証終)
(コメント) 上記証明の中に出てきた式: (m+n)AD2=na2+mb2−mn(m+n)
も魅力的な式である。書き直せば、
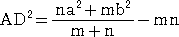
何となく、分点の公式に似ていて、覚えやすいかな?
(追記) 平成24年2月11日付け
数学の研究会で、開成高校の木部先生が、角の2等分線の長さの公式
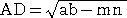
を紹介された。知っている公式なので、嬉しかった!いよいよこの公式も全国区かな?
(追記) 平成25年2月13日付け
上記では余弦定理を用いて証明したが、もっと簡便な方法があることを「角の2等分線」
におけるFNさんの証明を見て思った。
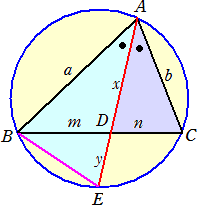 |
(証明) △ABE∽△ADE より、 a/(x+y)=x/b
すなわち、 x2+xy=ab
また、方べきの定理より、 xy=mn
したがって、 x2+mn=ab より、
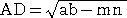
が成り立つ。 (証終) |
(コメント) この証明を見るとまさに裏技の証明に相応しい証明ですね!
絶対に忘れない...かな。
(追記) 平成25年9月28日付け
角の2等分線の長さを求めるのに「なぜ唐突に外接円?」ということで、土佐高校の藤岡優
太先生が次のような別解を考えられた。円を使わないごく自然な解法だと思う。
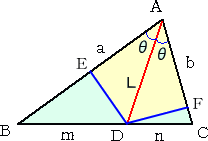 |
左図において、 △ABC=2△ADE+△BDE+△CDF
ここで、 △ABC=(1/2)absin2θ
△ADE=(1/2)Lsinθ・Lcosθ=(1/4)L2sin2θ
△BDE+△CDF=(1/2)mnsin2θ |
したがって、 (1/2)absin2θ=(1/2)L2sin2θ+(1/2)mnsin2θ より、
ab=L2+mn すなわち、 L2=ab−mn が成り立つ。
(コメント) 垂線を下ろして、三角形の面積を分割する発想に感動しました。
(追記) 平成24年8月29日付け
平成24年8月23日付けで、当HP読者のK.S.さんより、上記公式に関連する話題をメ
ールで頂いた。
ピタゴラスの定理の拡張で、「角の二等分線定理 AD×AD=AB×AC−BD×CD」が、
特に、二等辺三角形のとき、ピタゴラスの定理が成り立つ。
「ピタゴラスの定理」「余弦定理」「トレミーの定理」「角の二等分線定理」「中線定理」など幾
何的な証明がありますが、これらをそれぞれ直接に代数的に証明できるのではないでしょう
か?皆さんのお力を借りたいと思います。
(コメント) 上記のことを追認してみた。
 |
a=b のとき、 m=n で、∠ADB=90°である。
このとき、 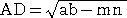 から、 から、
AD2=a2−m2 すなわち、
AD2+BD2=AB2
が成り立つ。(ピタゴラスの定理) |
(追記) 調和点列について
上記で述べたように、角の二等分線については興味ある、しかも有用な比に関する性質
がある。
△ABCの頂角Aの内角または外角の二等分線が辺BCまたはその延長と交わる点を
それぞれP、Qとおく。
このとき、 AB:AC=BP:PC=BQ:QC が成り立つ。
内角の場合は、上記で証明したが、次の図とにらめっこすると、明らかとなるであろう。
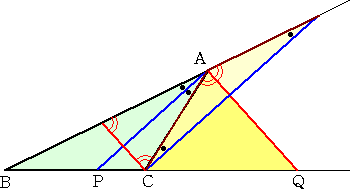
ところで、角の2等分線の性質を証明する場合、上図のように、角の2等分線と平行な直
線が肝要であったが、最近、角の2等分線に垂直な直線を考える場合もあることを知った。
○ 内角の2等分線の場合
 |
左図において、 △ABB’∽△ACC’
より、 AB:AC=BB’:CC’
また、 △BB’P∽△CC’P より、
BB’:CC’=BP:PC
よって、 AB:AC=BP:PC |
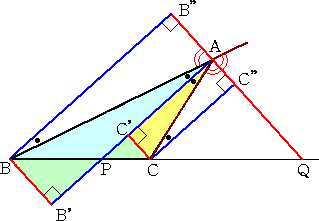
○ 外角の2等分線の場合
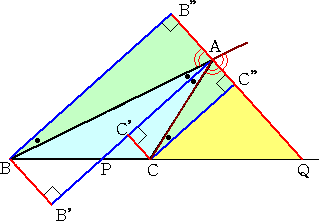 |
左図において、 △ABB”∽△ACC”
より、 AB:AC=BB”:CC”
また、 △BB”Q∽△CC”Q より、
BB”:CC”=BQ:QC
よって、 AB:AC=BQ:QC |
何れも、頂点B、Cより垂線を下ろすと覚えておけば、証明は容易に復元できるだろう。
ところで、一直線上に4点 B、C、P、Q があり、BP:PC=BQ:QC が成り立つとき、
これら4点のことを、調和点列というようだ。
同様の現象は、三角形における共点条件、共線条件においても見られる。
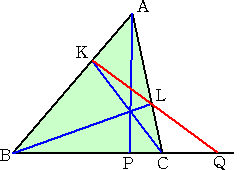 |
チェバ、メネラウスの定理から、
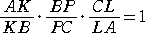 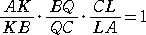
よって、
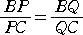
となり、4点 B、C、P、Q は調和点列となる。 |
角の二等分線、共点条件、共線条件と相異なる数学的事実ながら、その根底には調和
点列という共通の性質が秘められていることに驚かされる。
GAI さんからのコメントです。(令和4年4月21日付け)
上記を元にいろいろ計算をしていたら、
△ABCで、∠Aの二等分線が辺BCと交わる点をDとするとき、ADの長さは、
BD=m、CD=nであるならば、
AD=2mn・cos(A/2)/(m・cos(B)+n・cos(C))=2mn・sin((B+C)/2)/((m・cos(B)+n・cos(C))
で求められる、というものに出会ったのですが、これって妥当性を持ちますかね?
(理由) AB=a、AC=b とし、Dより、AB、ACへ下した垂線の足をE、Fとすると、AD^2=ab-mn
であるので、これが成立することから、
△BDE+△CDF
=△ABC−2△ADE=(1/2)absin(A)−2・(1/2)ADsin(A/2)・ADcos(A/2)
=(1/2)absin(A)−(1/2)AD^2・sin(A)=(1/2)mn・sin(A)
一方、 △BDE=(1/2)BD・DE・sin(π/2-B)=(1/2)m・AD・sin(A/2)・cos(B)
△CDF=(1/2)CD・DF・sin(π/2-C)=(1/2)n・AD・sin(A/2)・cos(C)
この2つを上式へ代入して整理すれば、
(1/2)AD・sin(A/2)・(m・cos(B)+n・cos(C))=(1/2)mn・sin(A) より、
AD=2mn・cos(A/2)/(m・cos(B)+n・cos(C))=2mn・sin((B+C)/2)/((m・cos(B)+n・cos(C))
が導けた。
(コメント) △BDE+△CDF=(1/2)mn・sin(A) という結果に、数学の深淵さ、美しさを
感じますね!
(追記) 令和5年6月28日付け
問題 下図のように、AB=12、B=90°の直角三角形ABCがあり、∠Aの2等分線が
辺BCと交わる点をDとする。
BD=4のとき、CD=x、AD=y、AC=z の長さをそれぞれ求めよ。
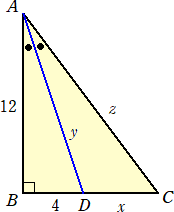
(解) 三平方の定理より、 y2=122+42=160 よって、 y=4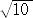
また、(x+4)2+122=z2 で、角の2等分線の性質から、12 : z=4 : x より、 z=3x
なので、上式に代入して、
x2+8x+16+144=9x2 すなわち、 x2−x−20=(x−5)(x+4)=0 から、x=5
このとき、 z=15 である。 (終)
x、z について、次のような別解も考えられる。
(別解) Dより辺ACに垂線を下ろし、その足をEとおくと、△ABD≡△AED なので、
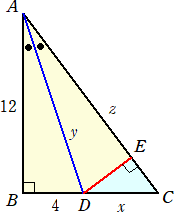
DE=4 、AE=12 である。さらに、△CDE∽△CAB より、DE:AB=4:12=1:3
したがって、△CDE=S とおくと、△CAB=9S なので、△ADE=4S=4・12/2=24
から、S=6 となる。このとき、CE・4/2=6 より、 CE=3 で、z=12+3=15
よって、x=15/3=5 となる。 (終)
(コメント) 角の二等分線の長さの公式 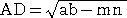 を用いて、
を用いて、
y2=12・15−4・5=160 から、y=4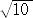 としてもよい。
としてもよい。
(追記) 令和6年7月28日付け
上記の問題に対して、次のような別解も考えられる。
(別解)
DE=4 、AE=12 である。さらに、△CDE∽△CAB より、DE:AB=4:12=1:3
したがって、△CDE=S とおくと、△CAB=9S なので、 △ABD=4S、△ADC=5S
よって、 4 : x=4S : 5S=4 : 5 から、 x=5 であることが分かる。
このとき、三平方の定理より、 z2=122+92=225 から、 z=15
y2=122+42=160 から、 y=4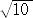 (終)
(終)
(別解) CD=x とおくと、ADは∠Aの2等分線なので、 AC=3x となる。
よって、三平方の定理より、 122+(x+4)2=9x2 から、x2−x−20=0
(x−5)(x+4)=0 より、 x=5
このとき、 z2=122+92=225 から、 z=15
y2=122+42=160 から、 y=4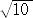 (終)
(終)
(別解) 線分ADに平行に線分EFを引き、BEとADの交点をGとおく。
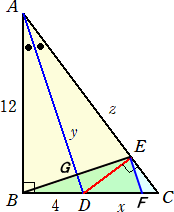
このとき、△ABD∽△BGD より、 BG : GD=12 : 4=3 : 1
そこで、 GD=m とおくと、 BG=GE=3m となる。このとき、 AG=9m から、
AD=10m となる。
GD : EF=BG : BE=3m : 6m=1 : 2 から、EF=2m となる。
よって、 EF : AD=2m : 10m=1 : 5 から、 EC : AC=1 : 5 なので、
EC : EC+12=1 : 5 より、 EC=3 となり、 z=12+3=15
また、 15 : 4+x=x : 3 より、 x2+4x−45=0 を解いて、 x=5
y2=122+42=160 から、 y=4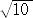 (終)
(終)
(追記) 令和6年7月29日付け
次の、角の二等分線の長さを求める問題には、いろいろな解法の可能性がある。
問題
 |
左図のような△ABCにおいて、AB=7、AC=8、
∠BAC=120° とする。線分ADが∠BACの2等
分線のとき、線分ADの長さを求めよ。 |
この問題に対しては、まず、面積利用が一般的だろう。
(解) △ABC=△ABD+△ADC より、
(1/2)・7・8・sin120°=(1/2)・7・AD・sin60°+(1/2)・AD・8・sin60°
よって、 56=15AD より、 AD=56/15 (終)
(別解) 余弦定理より、 BC2=72+82−2・7・8・cos120°=169 なので、BC=13
さらに、角の2等分線の性質から、 BD : DC=7 : 8 なので、
BD=91/15、DC=104/15 である。このとき、角の二等分線の長さの公式を用いて、
 |
AD2=7・8−(91/15)(104/15)=3136/225
より、 AD=56/15 (終) |
初等幾何を用いて、次のような別解も考えられる。
(別解) 正三角形ABEを作る。

このとき、AC BE となるので、AD : DE=8 : 7 より、
BE となるので、AD : DE=8 : 7 より、
AD=7×(8/15)=56/15 (終)
(コメント) この別解は、∠BAC=120°の場合しか使えないのは残念!
以下、工事中!














