
当HPの「角の二等分線の長さ」において、次の公式を示した。
角の二等分線の長さの公式
角の2等分線 
当HPの「角の二等分線の長さ」において、次の公式を示した。
角の二等分線の長さの公式
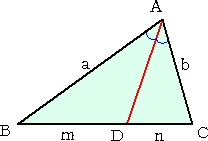 |
△ABC において、ADは∠Aの二等分線である。 このとき、 が成り立つ。 |
(追記) 平成24年2月11日付け
数学の研究会で、開成高校の木部先生が、角の2等分線の長さの公式
![]()
を紹介された。知っている公式なので、嬉しかった!いよいよこの公式も全国区かな?
角の2等分線について長さADを求める問題は多数あるが、∠ADCに注目し、その角の
大きさを求める問題は少ない。
例 △ABCにおいて、∠A=80°、∠B=30°、∠C=70°とする。∠Aの二等分線が
辺BCと交わる点をDとする。このとき、∠ADCを求めよ。
(解) ∠ADC+40°+70°=180°より、 ∠ADC=70° (終)
上記の解を見て分かるように、「三角形の内角の和は180°」という性質を使うだけで、
特別なことは何も起こらないように見える。それ故に、この手の問題は少ないのだろう。
これに対して、埼玉県立豊岡高校の五十嵐英夫先生が、次の性質に着目された。
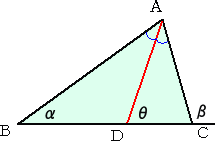 |
△ABC において、ADは∠Aの二等分線である。 このとき、 が成り立つ。 |
(証明) ∠A=β−α なので、 θ+(β−α)/2=β より、
θ=β−(β−α)/2=(α+β)/2 (証終)
この性質を用いれば、上記の例の問題は、∠ADC=(30°+110°)/2=70°となる。
また、五十嵐先生は、次の性質も示されている。
![]()
(証明) 角の2等分線の性質より、 BD : DC=AB : AC なので、
△ABCの高さを1とすると、
1/tanα−1/tanθ : −1/tanβ+1/tanθ=1/sinα : 1/sinβ=sinβ : sinα
が成り立つ。 よって、 cosα−sinα/tanθ=−cosβ+sinβ/tanθ より、
(sinα+sinβ)/tanθ=cosα+cosβ
すなわち、
![]()
が成り立つ。 (証終)
この公式は、α、βが具体的に分からない場合に有効だろう。
例 辺ABの傾きが 4/3 で、辺ACの傾きが −3/4 のとき、線分ADの傾きを求めよ。
(解) tanα=4/3 より、 sinα=4/5 、cosα=3/5
tanβ=−3/4 より、 sinβ=3/5 、cosβ=−4/5
よって、 tanθ=(4+3)/(3−4)=−7 (終)
(コメント) 今まで計算してきたはずなのに、上記のように公式化できるとは知りませんでし
た。五十嵐先生に感謝します。
角の2等分線に関して、次の性質があることを最近知ることが出来た。
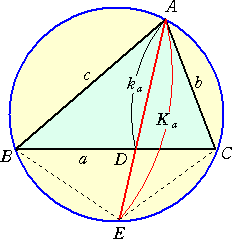 |
左図において、線分AEは∠Aの2等分線である。 このとき、 Ka・ka=bc が成り立つ。 |
(証明) 線分AEは∠Aの2等分線なので、 BD : DC = c : b である。
このとき、 BD=ac/(b+c) 、 DC=ab/(b+c)
△ABD∽△CED より、 ka : ac/(b+c) = ab/(b+c) : Ka−ka
よって、 (Ka−ka)ka=a2bc/(b+c)2 より、 Ka・ka=ka2+a2bc/(b+c)2
ところで、 ka2=c2+a2c2/(b+c)2−2ac2/(b+c)cosB において、
cosB=(c2+a2−b2)/(2ca) なので、
ka2=c2+a2c2/(b+c)2−2ac2/(b+c)・(c2+a2−b2)/(2ca)
=c2+a2c2/(b+c)2−c(c2+a2−b2)/(b+c)
=c{c(b+c)2+a2c−(c2+a2−b2)(b+c)}/(b+c)2
=c(b2c+2bc2+c3+a2c−bc2−a2b+b3−c3−a2c+b2c)/(b+c)2
=c(2b2c+bc2−a2b+b3)/(b+c)2
=bc(2bc+c2−a2+b2)/(b+c)2
=bc{(b+c)2−a2}/(b+c)2
=bc−a2bc/(b+c)2
したがって、
Ka・ka=ka2+a2bc/(b+c)2=bc−a2bc/(b+c)2++a2bc/(b+c)2=bc
となる。 (証終)
他の頂点に対しても同様のことを行えば、
Kb・kb=ca 、Kc・kc=ab
したがって、新たな公式
KaKbKc・kakbkc=(abc)2
が得られる。
(コメント) 何となく美しい公式ですね!
出張で横浜へ向かう電車の中で、上記のことを考えていたら、もっと初等的に証明できる
ことに気がついた。同様のことを、当HPがいつもお世話になっているHN「FN」さんからもご
教示いただいた。(平成23年6月16日付け)
(別証) ΔABDとΔAECにおいて、
∠ABD=∠AEC(弧ACの上に立つ円周角)
∠BAD=∠EAC(ADEは∠Aの2等分線)
よって、 ΔABD∽ΔAEC より、 AB : AD = AE : AC なので、 AB・AC=AD・AE
これより、 Ka・ka=bc (別証終)
(コメント) FNさんに感謝します。
(追記) 平成25年2月13日付け
角の2等分線の長さの公式
 |
△ABC において、ADは∠Aの二等分線である。 このとき、 が成り立つ。 |
上記を証明するのに、余弦定理を用いるよりも、もっと簡便な方法があることをFNさんの
証明を見て思った。
(証明)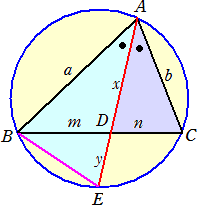 |
△ABE∽△ADE より、 a/(x+y)=x/b すなわち、 x2+xy=ab また、方べきの定理より、 xy=mn したがって、 x2+mn=ab より、 が成り立つ。 (証終) |
(コメント) この証明を見るとまさに裏技の証明に相応しいですね!絶対に忘れない...
かな。
(追記) 平成25年9月28日付け
角の2等分線の長さを求めるのに「なぜ唐突に外接円?」ということで、土佐高校の藤岡優
太先生が次のような別解を考えられた。円を使わないごく自然な解法だと思う。
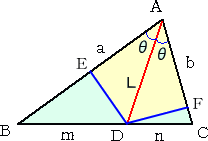 |
左図において、 △ABC=2△ADE+△BDE+△CDF ここで、 △ABC=(1/2)absin2θ △ADE=(1/2)Lsinθ・Lcosθ=(1/4)L2sin2θ △BDE+△CDF=(1/2)mnsin2θ |
したがって、 (1/2)absin2θ=(1/2)L2sin2θ+(1/2)mnsin2θ より、
ab=L2+mn すなわち、 L2=ab−mn が成り立つ。
(コメント) 垂線を下ろして、三角形の面積を分割する発想に感動しました。
(追記) 平成26年1月25日付け
角の2等分線というと、2等分線の長さを問うたり、線分の比を求める問題が多い。よく次
の図形が問題に用いられる。
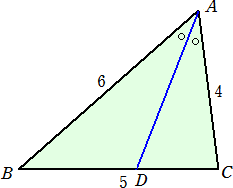
角の2等分線の性質から、BD : DC = 3 : 2 なので、BD=3、DC=2 となる。
さらに、上図の場合、 C=2B という関係式が成り立つ。このような関係式が成り立つこ
と自体初体験であるが、新しい問題への発展の可能性を秘めているような予感がする。
 |
辺AB上に、AE=AC=4 となる点Eをとると、明ら かに、△ACD≡△AEDとなり、その結果として、 △EBDは2等辺三角形 となる。よって、 ∠C=∠AED=2∠B より、 C=2B が成り立つ。 |
上記の、五十嵐英夫先生(埼玉県立豊岡高校)の結果を用いれば、
∠ADC=(∠B+180°−2∠B)/2=90°−∠B/2
であることも分かる。
(コメント) 「三角形の内角の和は180度」という関係はとても美しい。数式化すれば、
A+B+C=180°となる。上記の関係 2B−C=0 という関係もある意味で美しい。
実は、次の事実が知られている。
上記の△ABCの3辺の長さを、a=BC、b=CA、c=AB とすると、 c2=b(a+b) が、
成り立っている。このとき、一般に、
(a,b,c)=(γ2−β2,β2,βγ) (β、γは互いに素な自然数で、γ/2<β<γ)
と表される。逆に、三角形の3辺が上記の形に表されれば、必ず、2B−C=0 という関係
が成り立つ。
上記の△ABCは、β=2、γ=3 という場合である。β、γの値を変えれば、2B−C=0
という関係を持つ△ABCは無数に作ることができる。
(追記) 平成28年1月28日付け
当HPがいつもお世話になっているHN「GAI」さんからの出題です。
△ABCがあり、次の各条件下のAの角度はそれぞれ何?ただし、∠Aの2等分線が辺BC
と交わる点をDとする。
(1) ∠B : ∠C = 2 : 1 で、 AB = CD
(2) ∠A : ∠C = 2 : 3 で、 AB+CD = AC
しばらくぶりに考える時間が持てたので挑戦してみた。(1)は、何となく上記の「C=2B」
の場合の図が参考になりそうな...予感。(平成28年4月11日付け)
(解)(1) 題意より、∠B : ∠C = 2 : 1 即ち、∠B=2∠C なので、△ABD≡△AEDとな
るように点Eをとることができる。
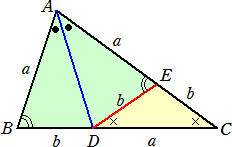
このとき、∠B=∠AED=∠EDC+∠C=2∠Cより、∠EDC=∠Cとなるので、△EDC
は2等辺三角形となる。
よって、AB = CD=a とおくと、AE=a で、BD=DE=EC=b とおけて、△ABCは、
CA=CB=a+b の2等辺三角形となる。
したがって、 ∠A+∠A+(1/2)∠A=180°より、 ∠A=72°となる。
(2) ∠A : ∠C = 2 : 3 より、 ∠C=3・(∠A/2) なので、∠A/2=θ とおくと、
∠C=3θ となる。また、AB+CD = AC より、 AC上に CE=CD となる点Eをとる。
このとき、 △CDEは2等辺三角形なので、 ∠CED=(π−3θ)/2
よって、 ∠AED=π−∠CED=(π+3θ)/2 である。
△ABD≡△AED なので、 ∠ABD=∠AED である。
ここで、 ∠ABD=π−3θ−2θ=π−5θ なので、 π−5θ=(π+3θ)/2
よって、 θ=(1/13)π となり、 ∠A=(2/13)π である。 (終)
(コメント) 最近このページに追記する機会があり、ページに再度目を通したら、なんと(2)
がながらく「工事中」になっていて気になっていました。ようやくほぼ6年ぶりに解決
することができました。GAI さん、答は合っているでしょうか?ご検分をお願いいた
します。(令和4年4月20日付け)
(追記) 平成31年3月25日付け
2018年度埼玉県公立高校入試問題です。三角形の相似や方べきの定理、トレミーの定
理と平面幾何大好き人間にとっては垂涎の逸品と言える問題です。
問題 円に内接する△ABCがあり、AB=5、AC=4とする。∠Aの2等分線が辺BCと交わ
る点をD、△ABCの内接円との交点をEとし、CE=![]() とする。このとき、線分ADの長
とする。このとき、線分ADの長
さを求めよ。
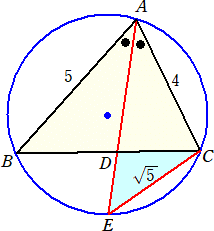
(解) AD=x とおくと、△ABD∽△CED なので、5 : x=![]() : CD より、CD=x/
: CD より、CD=x/![]()
同様にして、 △ACD∽△BED なので、 4 : ![]() =x : BD より、BD=
=x : BD より、BD=![]() x/4
x/4
また、 △ACD∽△CED なので、 4 : ![]() =x/
=x/![]() : DE より、DE=x/4
: DE より、DE=x/4
(方べきの定理より、x・DE=(![]() x/4)・(x/
x/4)・(x/![]() )=x2/4 なので、DE=x/4 としてもよい)
)=x2/4 なので、DE=x/4 としてもよい)
よって、トレミーの定理より、 5・![]() +4・
+4・![]() =(x+x/4)・(
=(x+x/4)・(![]() x/4+x/
x/4+x/![]() ) なので、
) なので、
9![]() =9
=9![]() x2/16 から、 x2=16 より、 x=4 (終)
x2/16 から、 x2=16 より、 x=4 (終)
(コメント) トレミーの定理を用いなくとも、△CED∽△AEC なので、
x/4 : ![]() =
=![]() : 5x/4 から、 x=4 が導かれる。
: 5x/4 から、 x=4 が導かれる。
また、角の2等分線の長さの公式を用いれば、
AD2=5・4−(![]() x/4)・(x/
x/4)・(x/![]() )=20−x2/4 から、 x2=20−x2/4
)=20−x2/4 から、 x2=20−x2/4
よって、 x2=16 より、 x=4 となる。
(追記) 令和3年1月29日付け
角の2等分線の公式を使う問題が中学校入試で出題された。大学入学センター試験の
前身の共通一次試験で平成元年頃から出題され、それが頻出の公式として定着している。
ただ、それが中学入試で、というのには驚かされる。正に中学入試、恐るべしである。
次は、灘中学の入試問題(改題)で、「えっ、これで求まるの?」というのが初見の感想であ
る。ただ、問題は美しく、いろいろな解法が考えられ、非常に解く者をワクワクさせる良問で
ある。
問 題 △ABCにおいて、頂点Aより底辺BCに垂線を下ろし、その足をHとおく。
BH=2、HC=5とする。また、∠ABC=2∠ACB とする。
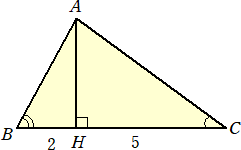
このとき、辺ACの長さを求めよ。
(解) ∠Bの2等分線と線分AHの交点をDとおくと、 △DBHと△ACHは相似なので、
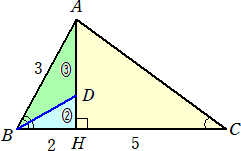 |
BH:CH=2:5 より、 DH:AH=2:5 なので、 AD:DH=3:2 となる。 角の2等分線の性質から、 AB=3 となる。 よって、 AC2=32-22+52=30 より、 AC= |
次のような別解も考えられる。
(別解) |
線分HC上に、AB=AE となる点Eをとると、 HE=BH=2 なので、 EC=3 となる。 △ECA、△ABEが2等辺三角形なので、 AB=AE=EC=3 よって、 AC2=32-22+52=30 より、 AC= |
(追記) 「正弦と比」と題して、当HPがいつもお世話になっているHN「よおすけ」さんから問
題を頂きました。(令和3年10月4日付け)
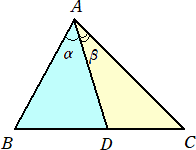 |
△ABCの辺BC上に点Dがある。 ∠BAD=α、∠CAD=β とおくと、 BD : DC=AB・sinα : AC・sinβ が成り立つことを証明せよ。 |
この問題で、AD⊥BCならば、等式が成り立つことは自明だろう。これが一般の場合も言
えるという点が面白い。
(解) 頂点Cより線分ADと平行な線を引き、直線ABとの交点をEとおく。
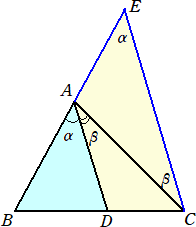
このとき、△ACEにおいて、正弦定理から、AC : AE=sinα : sinβ が成り立つ。
また、平行線の公理から、 AB : AE=BD : DC なので、 AE=AB×(DC/BD)
よって、 AC : AB×(DC/BD)=sinα : sinβ から、
AB・sinα×(DC/BD)=AC・sinβ すなわち、 BD/DC=(AB・sinα)/(AC・sinβ)
よって、 BD : DC=AB・sinα : AC・sinβ が成り立つ。 (終)
(コメント) 上記で、特に、α=β の場合は、線分ADは∠Aの2等分線となり、
BD : DC=AB : AC
が成り立つことを示す。このことから、よおすけさんの問題は、角の2等分線の公式の一般
化になっていることが分かる。
(追記) 令和3年10月13日付け
上記の、
 |
△ABCの辺BC上に点Dがある。 ∠BAD=α、∠CAD=β とおくと、 BD : DC=AB・sinα : AC・sinβ |
を示す問題で、よくよく考えたら、ADと平行な直線を引くまでもなく、直接的な証明が出来そ
うだ。
(別解) △ABDにおいて、正弦定理より、 BD/sinα=AB/sin∠ADB
同様に、△ADCにおいて、正弦定理より、 DC/sinβ=AC/sin∠ADC
したがって、 AB・sinα : AC・sinβ=BD・sin∠ADB : DC・sin∠ADC
ここで、 ∠ADB+∠ADC=π なので、 sin∠ADB=sin∠ADC
よって、 AB・sinα : AC・sinβ=BD : DC (終)
(追記) 令和3年10月14日付け
上記の証明が最も簡単だと思ったのも束の間、もっと簡単に証明できることを、当HP読
者のHN「T.K.」さんよりご教示いただいた。T.K.さんに感謝いたします。
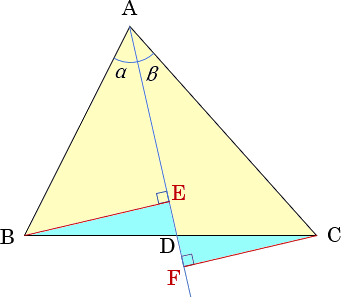 |
左図において、 △BDE ∽ △CDF より、 BD : DC =BE : CF =AB・sinα : AC・sinβ |
(追記) 令和4年4月16日付け
 |
上記で、角の2等分線が与えられたとき、次の公式が成 り立つことを見た。今では、これらの公式は受験数学の必 須アイテムといえるまでになった。 (1) a : b=m : n (2) |
これらの公式ほど有名ではないが、次の公式も角の2等分線の長さに関する基本公式で
ある。
(a+b)AD=2ab・cos(A/2)
(証明) △ABD+△ADC=△ABC より、
(1/2)a・ADsin(A/2)+(1/2)b・ADsin(A/2)=(1/2)absinA
すなわち、 (1/2)(a+b)・ADsin(A/2)=absin(A/2)cos(A/2)
よって、 (a+b)・AD=2abcos(A/2) が成り立つ。 (証終)
この公式と余弦定理を用いれば、(2) ![]() を示すことができる。
を示すことができる。
(証明) (a+b)AD=2ab・cos(A/2)=2ab・(a2+AD2−m2)/(2a・AD) より、
a・AD2=a2b−b・m2=a(ab−(b/a)m・m)
(1)より、 m=(a/b)n なので、 a・AD2=a(ab−(b/a)(a/b)n・m)=a(ab−mn)
よって、 AD2=ab−mn から、 ![]() である。 (証終)
である。 (証終)
GAI さんからのコメントです。(令和4年4月23日付け)
上記で、△ABCで∠Aの二等分線が辺BCと交わる点をDとし、AB=a、AC=b とするとき、
AD=2abcos(A/2)/(a+b)
なる公式を示してあるが、これは、a、bに対する調和平均 d
1/d=(1/2)(1/a+1/b) 即ち、 d=2ab/(a+b)
に対して、縮小率 cos(A/2) を掛けたものと解釈される。
ここに、調和平均の幾何的解釈として、(→ 参考:「調和平均の真実」)
xy平面で、x軸上の点A(a,0)、y軸上にP(0,d)をとり、点Pからx軸に平行に距離bだけ離
れた点B(b,d)を取るとき、4点O(原点)、A(a,0)、B(b,d)、P(0,d) が囲む台形に半径d/2
の円が内接できる。即ち、
2つの平行な長さ a、b の間隔を調和平均で出すdで離してやっておけば、この中にピタリ
半径d/2の内接円が収まり、その間隔dを、最後に∠BACの二等分角度A/2に対するcos量
のcos(A/2)で縮小してやれば、ADの距離が与えられると解釈される。
つまり、△ABCで∠Aの二等分線が辺BCと交わる点をDとし、AB=a、AC=b とするとき、
a と b の調和平均 d=2ab/(a+b) を求めれば、ADは、
AD=d・cos(A/2)
により与えられる。
(コメント) ADの計算に、a と b の調和平均が出てくるところが面白いですね。
(追記) GAI さんから問題をいただきました。(令和4年4月18日付け)
△ABCがあり、辺BCがx-y座標平面上のx軸上にあり、頂点Aはy軸の正の部分にあるも
のとする。
今、線分AB、ACの傾きをそれぞれm1、m2と表すとき、∠Aの二等分線が辺BCと交わる
点をDとしたとき、各(m1,m2)の値に対するADの線分の傾きmがどの様な値となるか、見
つけてほしい。
(1) (m1,m2)=(1/7,-1)
(2) (m1,m2)=(1/2,-2)
(3) (m1,m2)=(1/3,-3)
(4) (m1,m2)=(1/4,-4)
(5) (m1,m2)=(1,-5)
(コメント) 何となく、冒頭の五十嵐先生の着目された公式
 |
△ABC において、ADは∠Aの二等分線である。 このとき、 が成り立つ。 |
が使えそうな雰囲気だったので、計算してみた。
GAI さんの問題設定(1)〜(5)から、辺BC上に座標軸の原点がある。
このとき、m1=tanα、m2=tanβ であり、m=tanθである。
2θ=α+β なので、 tan2θ=(tanα+tanβ)/(1−tanαtanβ) である。
(1) m1=1/7、m2=−1 のとき、 tan2θ=−3/4
tan2θ=2tanθ/(1−tan2θ) に代入して整理すると、
3tan2θ−8tanθ−3=0 すなわち、 (3tanθ+1)(tanθ−3)=0
DはBO上にあるので、 tanθ=3
(2) m1=1/2、m2=−2 のとき、 tan2θ=−3/4
tan2θ=2tanθ/(1−tan2θ) に代入して整理すると、
3tan2θ−8tanθ−3=0 すなわち、 (3tanθ+1)(tanθ−3)=0
DはBO上にあるので、 tanθ=3
(3) m1=1/3、m2=−3 のとき、 tan2θ=−4/3
tan2θ=2tanθ/(1−tan2θ) に代入して整理すると、
2tan2θ−3tanθ−2=0 すなわち、 (2tanθ+1)(tanθ−2)=0
DはBO上にあるので、 tanθ=2
(4) m1=1/4、m2=−4 のとき、 tan2θ=−15/8
tan2θ=2tanθ/(1−tan2θ) に代入して整理すると、
15tan2θ−16tanθ−15=0 すなわち、 (5tanθ+3)(3tanθ−5)=0
DはBO上にあるので、 tanθ=5/3
(5) m1=1、m2=−5 のとき、 tan2θ=−2/3
tan2θ=2tanθ/(1−tan2θ) に代入して整理すると、
tan2θ−3tanθ−1=0 すなわち、 tanθ=(3±![]() )/2
)/2
DはBO上にあるので、 tanθ=(3+![]() )/2
)/2
らすかるさんからのコメントです。(令和4年4月18日付け)
一般式は、{m1*m2-1-√((m1^2+1)*(m2^2+1))}/(m1+m2) でしょうか。
(コメント) (m1+m2)tan2θ+2(1−m1m2)tanθ−(m1+m2)=0 を解くと、
tanθ=[m1m2−1±√{(m12+1)(m22+1)}]/(m1+m2)
ここで、点Dのx座標は、
x={(√(m22+1)−√(m12+1)}/{m2√(m12+1)−m1√(m22+1)}
m1>0、m2<0 より、 m2√(m12+1)−m1√(m22+1)<0 に注意して、
m1>−m2 のとき、 x>0 で、 tanθ<0 となるために、
tanθ=[m1m2−1−√{(m12+1)(m22+1)}]/(m1+m2)
m1<−m2 のとき、 x<0 で、 tanθ>0 となるために、
tanθ=[m1m2−1−√{(m12+1)(m22+1)}]/(m1+m2)
以上をまとめて、 tanθ=[m1m2−1−√{(m12+1)(m22+1)}]/(m1+m2)
GAI さんからのコメントです。(令和4年4月19日付け)
個別に出していたので、こんな式で表せるとは思ってもいませんでした。
これは、AB とACが直角なら(m1*m2=-1)、m=(1+m1)/(1-m1) の式に還元できるので、
m1=1 ==>m=∞
m1=1/2 ==>m=3
m1=2 ==>m=-3
m1=1/3 ==>m=2
・・・・・・・・
と対応していくから、BCを直径とする円を利用して、m1での値を使って作図することで、∠A
での二等分線が引けることができたり、他にも応用が出来そうですね。
(追記) 令和7年8月26日付け
次の東北大学 前期文系(1998)の問題は、条件を入射角、反射角の関係と捉えると考
えやすい。
問題 2点A(4,0)、B(0,2)を考える。線分AB上の点Pと x 軸上の点Qが
∠OPB=∠QPA (O:原点)を満たしている。直線OPの傾きをmとして、Qの x 座標を
m を用いて表せ。
(解) 題意より、直線ABの方程式は、x+2y=4
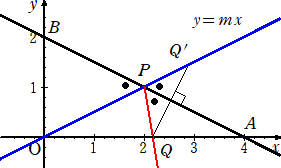
Q(t,0)、Q’(x,mx)とおくと、線分QQ’は直線ABに関して対称なので、
mx/(x−t)=2 、 (x+t)/2+2(mx/2)=4
すなわち、 (m−2)x=−2t 、 (2m+1)x=8−t から、xを消去して、
−2t(2m+1)=(8−t)(m−2) より、 t=(16−8m)/(3m+4) (終)
以下、工事中!