
確率論において、標準偏差の計算に「偏差の2乗の平均」が使われるように、数学におい
ては、各場面に応じて、いろいろな平均が考えられている。特に、次にあげる3つの平均は、
応用価値の高い重要な平均である。
相加平均(算術平均) 相乗平均(幾何平均) 調和平均
これらについては、既に当ホームページの別のページで言及済みなので、詳しくは、そち
らを参照してもらいたい。
調和平均の真実 
確率論において、標準偏差の計算に「偏差の2乗の平均」が使われるように、数学におい
ては、各場面に応じて、いろいろな平均が考えられている。特に、次にあげる3つの平均は、
応用価値の高い重要な平均である。
相加平均(算術平均) 相乗平均(幾何平均) 調和平均
これらについては、既に当ホームページの別のページで言及済みなので、詳しくは、そち
らを参照してもらいたい。
| ・いろいろな平均 | ・・・ | いろいろな平均の意味や作図方法について |
| ・質問に対する回答(2) | ・・・ | いろいろな平均の違いと実際の適用例について |
| ・ピタゴラス音階 | ・・・ | いろいろな平均と音楽の関係について |
このページでは、特に、調和平均について調べようと思う。
インターネットで、調和平均について検索をかけると、たくさんのホームページで、調和平
均のことが説明されている。その内容については、上記のページにある内容とほとんど同じ
である。
特に、調和平均の実際の使用例としては、「平均速度」が主に取り上げられ、説明がそこ
で終わってしまうのが通例である。
(例) 行きは時速40km、帰りは時速60km。それでは、平均速度は?
多分、この例では、40と60の平均(?)が50と暗算でできるので、答えの誤った方向
へ誘惑するカラクリが好まれる理由だろう。答えは、時速48kmなのだが、調和平均を
説明する事例としては有名だが、インパクトに欠けるきらいがある。
(例) 行きは時速80km、帰りは時速20km。それでは、平均速度は?
答えは、時速32kmで、答えの意外性を訴えるには十分かな?
調和平均の作図方法も興味深いが、調和平均の直感的理解を得るまでには至らず、何
かしらもやのかかった状態のまま過ごしてきているというのが私自身の率直な感想である。
調和平均・・・ 2数 a、b に対して、逆数の算術平均の逆数 |
||
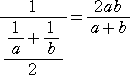 |
上記の定義からわかるように、調和平均を m とすると、3つの数 a、m、b は調和数列を
なす。(調和数列とは、各項の逆数からなる数列が、等差数列となるときをいう。)
すなわち、
![]()
が成り立つ。
このページでは、調和平均の直感的理解を得ることを目標としているが、上記の公式は、
まさにその出発点の公式である。
上式の分母を払って、 m(a+b)=2ab から、ma−ab=ab−mb
となる。
このとき、a(m−b)=(a−m)b から、比例式
a : b = a−m : m−b
が成り立つ。
この比例式から、下図のように、調和平均の直感的理解が可能となる。
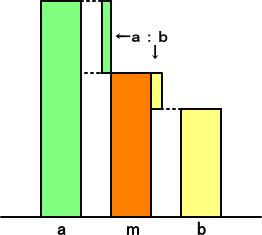
調和平均とは、互いの差の比が、もとの比と同じという、まさに周りに気を使った平均とい
う意味合いで、現代若者気質をみるようである。
上の比例式は、ピタゴラス学派の人々から、調和的相似と呼ばれ、上の計算を逆算する
ことにより、調和平均の関係式が導き出されている。
また、調和平均という言葉は、もともと音楽理論に用いられる言葉らしい。
いま、弦を同じ材質・同じ太さ・同じ強さで張ったとき、音の高さは弦の長さで決まる。上の
図で、a=36、b=18 とする。このとき、 a を「ド」の音とすれば、 b
は a よりも1オクターブ
高い「ド」の音を表す。このとき、調和平均 m は、24 となる。m は、a の2/3倍の値なの
で音楽理論では、m の音を、 a の音より完全5度上の音といい、「ソ」という音を表す。
一般に、長さ a の弦に対して、その半分の長さ(a/2)の弦をとる。このとき、この2つの数
の調和平均をとれば、その長さを持つ弦は、長さ a の弦に対して、完全5度上の音を表す。
弦の長さの比が、3:2 のとき、2つの音が最も美しい協和音になることを発見したのは、
ピタゴラスであるが、それが調和平均という数学の世界での姿を持っているということに驚
かざるをえない。
さらに、驚くべき事実がある。
今、任意に自然数 a を与える。b=a+1 として、調和平均 m を求めてみると、
![]()
となる。このとき、
(2a2+2a)2+(2a+1)2= (2a2+2a)2+4a2+4a+1
=(2a2+2a)2+2(2a2+2a)+1=(2a2+2a+1)2
が成り立つので、調和平均の分母と分子は、ピタゴラス数を与える。
ピタゴラスが求めた宇宙の神秘の比が、音楽にも数学にも深く関わっているという事実に
ピタゴラス学派の偉大さを感じいるばかりである。
(参考文献:イー・ヤー・デップマン 著 藤川 誠 訳 算数の文化史(現代工学社)
繁下和雄 著 実験音楽室(音楽之友社))
(追記) 上記で、調和平均の直感的理解を得る図を示したが、同様の図を用いることによっ
て、冒頭に述べた3つの重要な平均(相加平均・相乗平均・調和平均)の統一的理解が
可能となる。
相加平均の場合・・・・・ 2数 a、b に対して、相加平均を m とすると、
a−m : m−b = 1 : 1
が成り立つ場合である。

実際に、比例式を解けば、m の値は、
![]()
となる。
相乗平均の場合・・・・・ 2数 a、b に対して、相乗平均を m とすると、
a−m : m−b = ![]()
が成り立つ場合である。
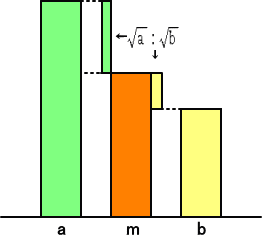
実際に、比例式を解けば、m の値は、![]() となる。
となる。
調和平均の場合・・・・・ 2数 a、b に対して、調和平均を m とすると、
a−m : m−b = a : b
が成り立つ場合である。

実際に、比例式を解けば、m の値は、
![]()
となる。
(追々記) 平成19年8月21日付け
調和平均の具体例として「平均速度」が有名であるが、次のような図の中にも調和平均が
隠れていて興味深い。
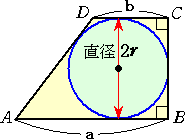 |
左図のような台形ABCDに直径 2r の円が内接してい る。このとき、 が成り立つ。 |
この問題は、一ノ関の和算家 千葉胤秀 が編集した「算法新書」(1830年)に掲載され
ている。
(注) 上記より、内接円の直径 2r は、台形の上底(=b)、下底(=a)の調和平均である。
実際に、三平方の定理により、 (a−b)2+(2r)2=(a−r+b−r)2
である。両辺を展開して整理すると、(a−b)2+4r2=(a+b)2−4r(a+b)+4r2
より、 4r(a+b)=(a+b)2−(a−b)2 すなわち、 2r(a+b)=2ab
よって、
![]()
が成り立つ。
(コメント) 上図から代数的な計算をしなくても、(相加平均)≧(調和平均) ということが
一目瞭然ですね!
(追記) 平成21年1月12日付け
1月10日付けで、大学生のHN「SPP」さんからメールを頂戴した。
調和平均に関して、ここ数日の間に繰り返し触れる機会があり、異なる内容の思わぬ関連
性に気づいたので報告します。
調和平均との遭遇 その1 ・・・ 「図形的意味」
「私の備忘録」-「調和平均の真実」で、その定義式と図形的意味を知る。
調和平均との遭遇 その2 ・・・ 「受験の問題」
学習塾で、高校受験の指導をしているとき、その1で目にした図形を背景とする問題を質
問され、問題の背景を思い出しつつ解答する。
調和平均との遭遇 その3
その2の翌日の大学の授業で、調和平均と相加平均の大小関係を利用した問題が登場。
内容は、株に1年間毎月投資する場合に、買う株数を決めるのと買う金額を決めるのでは、
一株あたりの購入金額が後者の方が安くなるというもの。後者の場合は毎月の株価の調和
平均が購入期間全体の株価となる。
調和平均との遭遇 その4
その3と同じ日の夕方、経済専攻の先輩に、その3の話題を提供すると、「その投資法は、
ドル=コスト平均法という」とのこと。その原理が調和平均で、図形的意味も知っている身に
は非常によく分かった。
調和平均の例というと、速さの場合ぐらいしか知らなかったが、今回、分散投資の例も頭
の中に加わった。ドル=コスト平均法に関しては、原理がごく単純な調和平均であることに
気づくことができた。普段から知識の関連付けが重要と知りつつ、なかなか具体的に実感
が得られない中で、偶然も重なったのか数日の間に調和平均関連の知識が得られました。
私も、調和平均の例をそれほど多く知らないので、この「ドル=コスト平均法」という話題は
新鮮であった。
この「調和平均の真実」は、2003年6月30日付けでアップロードし、2007年8月21日
に内容を一部補充した。今回は、大いに興味ある話題で、1年半ぶりの更新の機会を与え
ていただいたSPPさんに感謝します。
野村證券や三菱東京UFJ銀行、横浜銀行、・・・などで、投資関連のページを見ると、必
ず出てくるキーワードが、「ドル=コスト平均法」である。
「ドル=コスト平均法」(定額購入法)とは、
ランダムに価格変動のある商品を購入する場合、
価格変動による影響を抑制し価格変動リスクを分散するために、一定の金額で商品
を購入する方法
のことをいう。1940年代にアメリカで開発された方法で、例えば、毎月1万円分だけ純金
を積み増していく「純金積立」などが有名だろう。
キャッチコピー風に表せば、
安いときにたくさん 、 高いときは少しだけ
とでもなるだろうか...。
この方法に対するものとして、一定の数量を継続的に購入する方法などがある。この方
法に比べ、「ドル=コスト平均法」は、購入平均価格が安く済むという長所があるとのこと。
ただ、実際の投資の場面では、有利な場合、不利な場合ともに起こりうることに注意が
必要らしい。要するに、投資は「生き物」で、その場その場を臨機応変に対応しなければ
いけないということかな?私には到底できそうにない分野ですね!
ランダムに価格変動する商品を、一定額購入の場合と一定量購入の場合で、本当に、
「一定額購入の場合」の方が有利であることを具体例で確認しておこう。
| 株 価 | ドル=コスト平均法 | 一定量購入法 | |||||
| 購入金額 | 購入株数 | 平均株価 | 購入株数 | 購入金額 | 平均株価 | ||
| 1ヶ月目 | 100 | 2000 | 20 | 100 | 20 | 2000 | 100 |
| 2ヶ月目 | 200 | 2000 | 10 | 133 | 20 | 4000 | 150 |
| 3ヶ月目 | 400 | 2000 | 5 | 171 | 20 | 8000 | 233 |
| 4ヶ月目 | 100 | 2000 | 20 | 145 | 20 | 2000 | 200 |
上記の表からも分かるように、確かに「ドル=コスト平均法」の方が、安く株を購入するこ
とが出来る。これが銀行等のHPで盛んに一定金額での継続的購入を勧める根拠らしい。
実のところ、「ドル=コスト平均法」における平均株価は「調和平均」で、一定量購入法に
おける平均株価は「相加平均」である。
実際に、毎月一定額 K(円)で株を購入するとする。第k期の株価を ak(円)とすると、
購入株数は、 K/ak (株) となるので、平均購入株価は、
NK/(K/a1+K/a2+・・・+K/aN)=N/(1/a1+1/a2+・・・+1/aN)
これは正しく、株価 a1、a2、・・・、aN の調和平均である。
これに対して、毎月一定量 L (株) を購入する場合の平均購入株価は、
(a1L+a2L+・・・+aNL)/NL=(a1+a2+・・・+aN)/N
これは正しく、株価 a1、a2、・・・、aN の相加平均である。
このとき、(相加平均)≧(調和平均) ということから、上記で述べたことは当然の帰結
なのだ!
(コメント) 調和平均が、こんなに社会のお役に立っていることを知り、ある意味で感動しま
した!
さらに、調和平均もどきの問題を一つ...。
食塩の濃度 a %の食塩水 A が m (リットル)、食塩の濃度 b %の食塩水
B が
n (リットル)ある。いま、溶液 A 、 B それぞれから、x (リットル)取り出し、溶液 A
のものは溶液 B に、溶液 B のものは溶液 A に入れてかき混ぜる。
このとき、混合した後の溶液 A 、 B の濃度が等しくなるように x の値を定めよ。
濃度が等しくなるということなので、その濃度は、
{(a/100×m+b/100×n)/(m+n)}×100=(am+bn)/(m+n)
・・・ これは、加重平均( → 参考 : 「加重平均の底力」)
よって、{(a/100×m−a/100×x+b/100×x)/m}×100=(am−ax+bx)/m
より、 (am−ax+bx)/m=(am+bn)/(m+n)
分母を払って整理すると、 (b−a)(m+n)x=(b−a)mn より、x=mn/(m+n)
ここで、移動される総量 2x=2mn/(m+n) に注目すると、これは、調和平均!
(コメント) 濃度は一切関係なく、溶液の量のみで決まるとは驚きです!
(追記) 当HPの掲示板「出会いの泉」に、読者のHN「シーゲル」さんが平成24年9月14日
付けで、調和平均が現れる例について書き込みをされた。
調和平均が現れる例として一般的に、まずは平均速度が挙げられるようです。皆さん既に
ご存知かも知れませんが、以下のような初等的な力学の問題は如何でしょうか。
天井から吊るされた滑車に掛かった糸の両端に各々質量m1とm2のおもり1と2を吊り下げ
ます。(仮に、m1<m2としておく)重力により、m2が下向きに、m1が上向きに加速度運動を
はじめます。この加速度をa、重力加速度をg、糸の張力をT とすると、基本方程式は、
m1・a = T - m1・g ----- (1) 、 m2・a = m2・g -T ----- (2)
となり、両式からT を求めると、T = 2m1m2g/( m1+m2) を得ます。
ここで実効的質量として、T = μg とおけば、
1/μ = (1/m1 + 1/m2)/2
となり、張力に着目すれば、ふたつの質量の調和平均で表される実効的質量をもつおもりが
糸に吊るされていると見なすことができるでしょう。
(コメント) なるほど...。初見でした。シーゲルさんに感謝します。