
次の弦の長さにより決まる音階を、ピタゴラス音階という。音楽の歴史では、最も古い音階
だといわれる。古代ギリシャの数学者ピタゴラスは、鍛冶屋の槌の音に心地よく響き合う音が
あることに気づき、美しい協和音に秘められた「神のわざ」を探し求めようとした。
ピタゴラス音階 
次の弦の長さにより決まる音階を、ピタゴラス音階という。音楽の歴史では、最も古い音階
だといわれる。古代ギリシャの数学者ピタゴラスは、鍛冶屋の槌の音に心地よく響き合う音が
あることに気づき、美しい協和音に秘められた「神のわざ」を探し求めようとした。
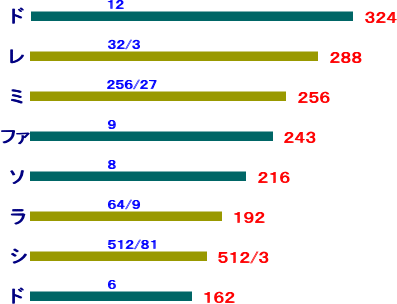 |
彼は、弦の長さの比に注目 して、2対1、3対2 のとき、 2つの音が最も美しい協和音 になることを発見した。 今日、前者は完全8度、後 者は完全5度の協和音とい われている。 また、4対3 のときは、完 全4度の協和音という。 このような性質を持つ数の 組として、 12 8 6 と、 12 9 6 が知られている。 |
このとき、 12 9 8 6 に対応して、ド・ファ・ソ・ド がまず決定される。
他の音は、この4音を基本として、次のようにして定められる。
「レ」の音 ・・・ ソの音と完全4度の音
すなわち、X : 8 = 4 : 3 より、X=32/3 として、弦の長さが定まる。
「ラ」の音 ・・・ レの音と完全5度の音
すなわち、32/3 : X = 3 : 2 より、X=64/9 として、弦の長さが定まる。
「ミ」の音 ・・・ ラの音と完全4度の音
すなわち、X : 64/9 = 4 : 3 より、X=256/27 として、弦の長さが定まる。
「シ」の音 ・・・ ミの音と完全5度の音
すなわち、256/27 : X = 3 : 2 より、X=512/81 として、弦の長さが定まる。
以上で定まる弦の長さをもとに、実際に楽器を作ってみたら、どんな風に聞こえるのだろう。
時間があったら、是非作ってみたいものだ。みなさんも、いかがですか?
さらに、6、8、9、12 の4つの数に、6の完全8度の数としての 3 を付け加えてみると、
3 6 8 9 12
の5つの数の間に、数学的に美しい関係が成り立つ。
6 は、3 と 12 の相乗平均である。(相乗平均については、こちら)
8 は、6 と 12 の調和平均である。(調和平均については、こちら)
9 は、6 と 12 の相加平均である。(相加平均については、こちら)
数学的に美しいということは、音として聞いても美しいということで、ピタゴラスがひたすら
求めた「宇宙の本質」というものの雰囲気が何となく伝わってくるような気がする。
(参考文献:船山良三 著 身近な数学の歴史(東洋書店))
(追記) ピタゴラス音階は弦の長さで決められたが、我々が通常聞いている音階は振動数
の比で決められたものである。(弦の長さと振動数は反比例する!)
1939年の国際会議で、「ラ=A」の振動数は、440Hzと定められた。この「ラ」の振動数
をもとに
| 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 |
| ド | レ | ミ | ファ | ソ | ラ | シ | ド |
という振動数の比で定まる音階を純正律音階という。
この音階では、「ドミソ」の和音の振動数の比が、 1 : 5/4 : 3/2
= 4 : 5 : 6 という
美しい比になっている。
ただ、純正律音階では転調するのが難しい。そこで、1オクターブあたり12個の鍵盤で、
どのように転調しても振動数の比が変わらないように決められたのが平均律音階である。
平均律音階では、振動数は半音上がる毎に一定の比率(=約1.06(正しくは、21/12))
で増えていく。即ち、(21/12)12=2 より、1オクターブ上がると、振動数は2倍(弦の長さは
1/2倍)になる。
| 1 | 22/12 | 24/12 | 25/12 | 27/12 | 29/12 | 211/12 | 2 |
| ド | レ | ミ | ファ | ソ | ラ | シ | ド |
数学者メルセンヌ(1588〜1648)によって1636年に、ほぼ完璧な12平均律の計算が完成
したという。
ピアノやギターなどの楽器のほとんどは平均律で調律されていて、一番馴染みがある音
階である。平均律の考えでは、弦の長さが指数関数 y=a・(1/2)x 的に変化するので、
グランドピアノを上から見ると、指数関数の、美しい単調減少のグラフが見て取れる。
ただ、平均律は転調はしやすいという利点はあるが、和音の美しさという点で多少負い目
がある音階である。
(コメント) 昔から音楽と数学は関係が深いと言われていますが、これほど数学の理論が
使われているとは驚きです。1秒間に440回振動する音が「ラ」というのも面白い
し、「ラ」の音を基準にするのも面白いですね!何でも、赤ちゃんの産声が世界共
通で、この「ラ」の音だとか...。
(追々記) 平成19年2月28日付けで、当HPの掲示板「出会いの泉」に、「おたぬき」さん
の書き込みがあった。「おたぬき」さんに感謝いたします。
ギター、マンドリンと言ったフレット楽器は、平均律にしか調律できません。これは、フレット
が平均律で切られているからです。
私自身、「フレットって何?」という状態だったので、いろいろ調べてみた。
「フレット」というのは、ギターの細長い棒(この部分を「ネック」というらしい!)に平行に
何本かついている金属製の仕切り(?)のことということを知りました。
確かに、各弦に共通の仕切りなので、「平均律で切られている」ことが分かりますね!
「Wikipedia」で、「フレット」の項をみると、弦毎にフレットの位置を変えて純正律の音階を
完全に演奏できるようにした「フレットボード」が考案されているとか...。
音楽の世界は、まさに「こだわりの世界」ですね!