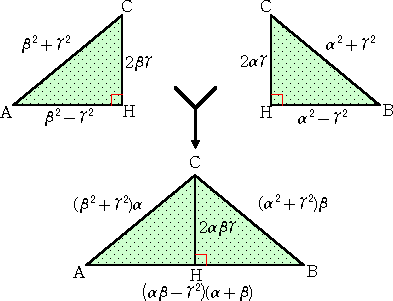ヘロン数とピタゴラス数 
C=90°の直角三角形ABCの三辺 a、b、c について、有名な三平方の定理
c2=a2+b2
が成り立つ。このとき、三辺 a、b、c が全て整数となるものを、ピタゴラス数という。
(詳しくは、こちらを参照)
また、そのような三角形は、ピタゴラス三角形と呼ばれる。
任意の自然数 α>β に対して、ピタゴラス数は、次の3つの数の組で与えられる。
c=α2+β2 、 a=α2−β2 、 b=2αβ
例 (α,β)=(2,1)のとき、 c=5、a=3、b=4
(α,β)=(3,1)のとき、 c=10、a=8、b=6 (これは、c=5、a=3、b=4に相似)
(α,β)=(3,2)のとき、 c=13、a=5、b=12
(α,β)=(4,1)のとき、 c=17、a=15、b=8
(α,β)=(4,2)のとき、 c=20、a=12、b=16 (これは、c=5、a=3、b=4に相似)
(α,β)=(4,3)のとき、 c=25、a=7、b=24
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
ピタゴラス数は、c<100の範囲で、16個あることが知られている。
(a,b,c)=(3,4,5)、(5,12,13)、(15,8,17)、(7,24,25)、(21,20,29)、
(9,40,41)、(35,12,37)、(11,60,61)、(45,28,53)、(33,56,65)、
(13,84,85)、(63,16,65)、(55,48,73)、(39,80,89)、(77,36,85)、
(65,72,97)
因みに、c<10000の範囲では、1593個あることが知られている。範囲が100倍になる
とその個数も大体100倍になるんですね!
ここで、c<100の範囲での16個のcの値をボーッと眺めていると、
5=4・1+1
13=4・3+1
17=4・4+1
25=5・5=(4・1+1)(4・1+1)
29=4・7+1
37=4・9+1
41=4・10+1
53=4・13+1
61=4・15+1
65=5・13=(4・1+1)(4・3+1)
73=4・18+1
85=5・17=(4・1+1)(4・4+1)
89=4・22+1
と必ずcの素因数は4で割ると1余る数であることに気づかされる。
(→ 参考:「4n+1型素数の性質」)
実は、次のことが知られている。
整数nがピタゴラス三角形の斜辺の長さであるための必要十分条件は、
nの素因数がすべて4で割ると1余ることである。
例 この事実から、斜辺の長さが21であるピタゴラス三角形は存在しないことが分かる。
実際に、 21=3・7 で、 3≡3 (mod 4)、7≡3 (mod 4) だからである。
さて、このピタゴラス数を用いて、ヘロン数といわれるものが作られることを最近知った。
三角形の三辺とその面積が全て整数となるものを、ヘロン数といい、そのような三角形は、
ヘロン三角形と呼ばれる。
任意の自然数 α≧β>γ に対して、次の4つの数の組:
a=(α2+γ2)β、b=(β2+γ2)α、c=(αβ−γ2)(α+β)、
S=αβγ(αβ−γ2)(α+β)
は、ヘロン数となる。このヘロン数は、ピタゴラス数を用いて、次のように考えることで容易に
得られる。
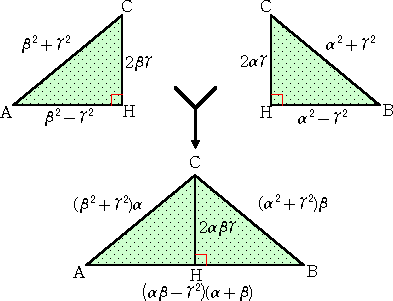
(注意) ヘロン数に関して、広島工業大学の大川研究室より、以下のことをご教示頂きまし
た。
上記のヘロン数の構成では、ピタゴラス三角形を2つ考えて合成した。したがって、少なく
とも一つの底辺に対する高さが整数となる。しかし、一般のヘロン三角形では、いつもそう
なるとは限らない。どの辺を底辺としても、それに対する高さが整数とならない場合がある。
例えば、a=5、b=29、c=30、S=72 の場合である。
ところで、この三角形は5倍すると、ピタゴラス三角形を2つ組み合わせた三角形になる。
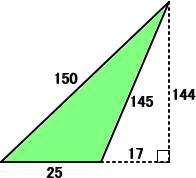
一般に、ヘロン三角形は、何倍かすると、ピタゴラス三角形の組み合わせとなる。
(追記) 三角形の三辺とその面積が全て整数となるものを、ヘロン数といったが、その
中で、三辺の長さの和(三角形の周の長さ)が面積と等しくなる場合がある。
ピタゴラス数からは、 (5 , 12 , 13)、(6 , 8 , 10)
実際に、三角形の三辺の長さが、(5 , 12 , 13)のとき、
周の長さは、5+12+13=30 、面積は、 5×12÷2=30
で、確かに成り立つ。 (6 , 8 , 10)も同様である。
ヘロン数からは、 (7 , 15 , 20)、(6 , 25 , 29)、(9
, 10 , 17)
実際に、三角形の三辺の長さが、(7 , 15 , 20)のとき、
周の長さは、7+15+20=42 、面積はヘロンの公式を用いて、S=42
で、確かに成り立つ。 他も同様である。
(コメント) 作問の時に、この事実を知っていると便利ですね!
(追記) 任意の自然数 α>β に対して、X=α2−β2 、Y=2αβ とおくと、
X2+Y2=(α2−β2)2+(2αβ)2=(α2+β2)2
が成り立つ。
この性質を利用すると、次のような問題にも即答できるだろう。
問題 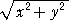 が自然数となるような x 、 y を求めよ。
が自然数となるような x 、 y を求めよ。
答は、明らかに、x=α2−β2、y=2αβ (α、βは自然数)である。
この問題を少しだけ一般化した次の問題も同様である。
問題 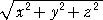 が自然数となるような x 、 y 、z を求めよ。
が自然数となるような x 、 y 、z を求めよ。
答は、x=α2+β2−γ2、y=2αγ、z=2βγ (α、β、γは自然数)である。
実際に、 x2+y2+z2=(α2+β2−γ2)2+(2αγ)2+(2βγ)2
=α4+β4+γ4+2α2β2−2β2γ2−2γ2α2+4γ2α2+4β2γ2
=α4+β4+γ4+2α2β2+2β2γ2+2γ2α2
=(α2+β2+γ2)2 から明らかだろう。
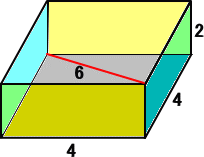
左図のような直方体で、辺と対角線の長さをともに整
数にしたい場合、上記公式は有効である。
(左図では、α=2、β=γ=1 としている。)
(参考文献:深川英俊、ダン・ソコロフスキー 著
日本の数学 何題解けますか?(上) (森北出版))
(追記) 平成19年3月31日付け
上記の問題で考えた
各辺の長さ、対角線の長さがともに自然数である直方体を見いだす
ことは、いろいろな問題設定で活用出来るだろう。
この話題をもう少し掘り下げることにする。
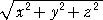 を、T とおいて、方程式 x2+y2+z2=T2 を考える。
を、T とおいて、方程式 x2+y2+z2=T2 を考える。
上記で、自然数 α、β、γに対して、
x=α2+β2−γ2 、 y=2αγ 、 z=2βγ 、 T=α2+β2+γ2
が方程式を満たすことを確認した。 したがって、解は無数にある。
この解の様子から、次の性質の成り立つことが分かる。
(1) 3数 x 、 y 、 z のうち、少なくとも2つは偶数である。
実際に、 自然数の平方数を、4で割った余りは、0 または 1 であることから
| |
| x2 |
1 |
1 |
1 |
0 |
| y2 |
1 |
1 |
0 |
0 |
| z2 |
1 |
0 |
0 |
0 |
| x2+y2+z2 |
3 |
2 |
1 |
0 |
|
となり、 x2+y2+z2=T2 が適するのは、3数 x 、 y 、 z のうち、少なくとも2つが偶数で
ある場合のみである。(上記の表は、mod 4 で考え、x2≧y2≧z2 (mod 4)とする。)
(2) 4数 x 、 y 、 z 、 T のうち、少なくとも1つは 3 の倍数である。
実際に、3数 x 、 y 、 z が何れも3の倍数でないとすると、それらの平方数は何れも 3
で割った余りは 1 だから、 x2+y2+z2=T2 は、3 の倍数となる。
よって、 T は、3 の倍数となる。
(3) 2つの0以上の整数 m 、 n に対して、
x=2m+1 、 y=2n 、 z=2m2+2n2+2m 、 T=2m2+2n2+2m+1
または、
x=2m 、 y=2n+1 、 z=2m2+2n2+2n 、 T=2m2+2n2+2n+1
も方程式を満たす。
このことは、計算により簡単に確かめられる。
(4) (1)から、 2つの自然数 m 、 n に対して、
x=2m 、 y=2n のとき、 z=m2+n2−1 、 T=m2+n2+1
も方程式を満たす。
このことは、計算により簡単に確かめられる。
(コメント) この(4)の形が一番スッキリした表現になっているかな?
上記の(3)、(4)から、 直方体の2辺を任意に与えても(ただし、ともに奇数は除く)、必
ず、方程式 x2+y2+z2=T2 を満たす自然数解が存在することが分かる。
問題作成に重宝するように、いくつかの具体例をあげておこう。
| |
| x |
1 |
1 |
2 |
2 |
4 |
6 |
| y |
2 |
4 |
3 |
6 |
4 |
6 |
| z |
2 |
8 |
6 |
9 |
7 |
7 |
| T |
3 |
9 |
7 |
11 |
9 |
11 |
|
上記の表からも察せられるように、次の事実が成り立つことは誠に残念である。
(5) 直方体の対角線の長さが自然数で、3辺の長さが連続する3整数となるものは
存在しない。
実際に、そのような解が存在するとすると、(1)から、真ん中の数は奇数で、3つの数は、
2m 、 2m+1 、 2m+2 (mは自然数)
と書ける。 このとき、
T2=(2m)2+(2m+1)2+(2m+2)2=6m2+12m+5
で、T2 を、3で割った余りは、2 となる。
ところが、自然数の平方数を、3で割った余りは、0 または 1 なので、これは矛盾。
したがって、条件を満たす直方体は存在しない。
(参考文献:シェルピンスキー 著 銀林 浩 訳 ピタゴラスの三角形 (東京図書))
(追記) 公差4のヘロン三角形について当HPがいつもお世話になっているHN「ハンニバル
・フォーチュン」さんからのご質問です。(平成30年12月13日付け)
3辺の長さと面積の全てが整数となる三角形をヘロン三角形と呼びます。3辺の長さが
互いに素で、公差4の等差数列となるようなヘロン三角形はあるのでしょうか。
(3辺の長さが、公差1^2の等差数列となるようなヘロン三角形はしばしば取り上げられて話
題になるようですけれども、公差2^2だとどうなのかと気になりました。)
また、公差が9ならばどうなりますでしょうか?
私は上記について何もわからないですけれども、皆様のお知恵をお借りしたく存じます。何
卒宜しくお願い申し上げます。
らすかるさんからのコメントです。(平成30年12月13日付け)
<公差4のとき>
辺の長さを、k、k+4、k+8 とすると、ヘロンの公式により、面積は、
S=(k+4)√{3(k+12)(k-4)}/4 すなわち、 16S^2=3(k+12)(k-4)(k+4)^2
となるが、互いに素という条件から、k は奇数なので、左辺は偶数、右辺は奇数となり、あり
得ない。
<公差9のとき>
辺の長さを、k、k+9、k+18 とすると、ヘロンの公式により、面積は、
S=(k+9)√{3(k+27)(k-9)}/4
となるが、右辺が整数になるためには、(k+27)(k-9) が3の倍数でなければならない。
よって、k が3の倍数でなければならないので、k、k+9、k+18 が互いに素とならず不適。
よって、あり得ない。
# 公差が偶数の場合は、公差が4の場合と同じ証明によりあり得ません。公差が奇数の場
合は、公差によってはあり得ます。
公差121のとき、 (123,244,365) (面積 3294)
公差169のとき、 (219,388,557) (面積 32010)
公差529のとき、 (579,1108,1637) (面積 157890)
公差1369のとき、 (1669,3038,4407) (面積 1731660)
公差2209のとき、 (2977,5186,7395) (面積 6098736) 等々。
「A072330」によると、公差が12k±1型の素数の積の場合のみあり得るそうです。
(よって公差25、49などはあり得ないことになります。)
GAI さんからのコメントです。(平成30年12月13日付け)
公差11なら、 (a,b,c)=(15,26,37)、(17,28,39)
公差13なら、 (a,b,c)=(15,28,41)、(25,38,51)
とか可能です。
ハンニバル・フォーチュンさんからのコメントです。(平成30年12月13日付け)
もろもろご教示を頂きまして、まことに有り難うございます。素早く素晴らしい御回答に感謝
いたします。ここで、
ヘロン三角形の面積は2の倍数である
ことの別証明らしきものを投稿させて下さい。御批正を頂きたく宜しくお願い致します。
ヘロン三角形で、3辺の辺長を a、b、c とし、その半周長を s 、面積を S とします。
公式より、 s=(a+b+c)/2 、S^2=s(s-a)(s-b)(s-c) ……(1) です。
(1)の右辺の4つの因数のうち、どれかひとつでも偶数であると示せれば、S^2は偶数となり、
S が偶数であることになります。
この目的のため、以下を示します。
イ) s が偶数のケースでは、(1)より S が偶数であることは自明です。
ロ) s が奇数のケースでは、a、b、c のうち少なくともひとつが奇数であること、すなわち、
(s-a)、(s-b)、(s-c) のうち少なくともひとつは偶数であること、従って、(1)より S が偶数で
あることを示します。
背理法により示します。s が奇数で、a、b、c が全て偶数であるようなヘロン三角形が存在
すると仮定します。
このとき、x=(b+c-a)/2、y=(c+a-b)/2、z=(a+b-c)/2 とおくと、a=y+z、b=z+x、c=x+y
a、b、c が全て偶数と仮定していますから、x、y、z は自然数です。
そこで、(1)の右辺を、x、y、z で表記すると、 S^2=(x+y+z)xyz ……(2)
ここで、x、y、z が全て奇数ということはありません。なぜならば、x、y、z が全て奇数だとす
ると、(2)の右辺は4で割ると3余る数であり、左辺は4で割ると1余る数だからです。
即ち、x、y、z のうち少なくともひとつは偶数です。x+y+z=s は奇数と仮定していましたから、
x、y、z のうち2つは偶数で、残るひとつが奇数となりました。
一般性を失うことなく x を奇数とし、y、z を偶数とできます。すると、a、b、c のうち、a が偶
数、b、c は奇数と結論づけられます。これは矛盾です。
よって、sが奇数のときには、a、b、c のうち 少なくともどれかひとつは、奇数であることが
証明されました。
以上から、sが奇数のときには、 (s-a)(s-b)(s-c) が偶数であると示されていますから、S^2
が偶数です。
イ)、ロ)いずれにしても S^2 が偶数ですから、Sもまた、偶数です。
#もうちょっとスッキリできないものかと考えましたが、ギブアップしました。わざわざ背理法を
使わなくともよさそうなものですけれども……。
DD++さんからのコメントです。(平成30年12月14日付け)
背理法を使うのであれば、最初からSが奇数と仮定した方が速いですね。ということで、証
明の本質部分を引き継いだままスッキリさせてみました。
(ヘロン三角形なら周長は偶数、という部分は明らかってことでいいんですかね?)
(証明) 背理法を用います。S を奇数であると仮定します。
S^2 は4で割ると1余る数です。
ところで、4で割ると1余る数を4つの自然数の積で書くとき、それらは全て奇数でなければ
ならず、
「4で割った余りが1である数ばかり4つ」
「4で割った余りが1である数と3である数が2つずつ」
「4で割った余りが3である数ばかり4つ」
のいずれかです。これらはいずれの場合も4数の和が4の倍数となります。
さて、S^2=s(s-a)(s-b)(s-c) という式に戻ります。
これは、「4で割ると1余る数を4つの自然数の積で書くとき」に当てはまります。
よって、sは奇数です。一方で、右辺の4つの数の和は4の倍数となるので、
s+(s-a)+(s-b)+(s-c)=4s-(a+b+c)=4s-2s=2s は4の倍数、つまり、s は偶数です。
これは、s が奇数であることに矛盾します。
したがって、仮定は誤りであり、Sは偶数です。 (証終)
ハンニバル・フォーチュンさんからのコメントです。(平成30年12月15日付け)
ぐっと簡明になりました。まことにありがとうございました。
ハンニバル・フォーチュンさんからのコメントです。(平成30年12月17日付け)
知人から聞いてビックリしたところなのですけれども、
任意のヘロン三角形は、回転と平行移動とをうまくほどこすと、3頂点全てを同時に
(平面上の単位長の)正方格子点に重ねることができる
…のだそうです。
複素平面上で考えたほうが、この性質を証明しやすいものなのでしょうか?
複素数平面を使わずにより初等的に証明する方法があるものなのでしょうか?
ヘロン三角形を何らかの基準で分類してタイプ別に考えるべきでしょうか?
2つのピタゴラス三角形の和ないし差としてヘロン三角形をあらわしたときに
格子点に乗ることは自明となるのでしょうか?あるいは、反例があるものなのでしょうか?
ハンニバル・フォーチュンさんからのコメントです。(平成30年12月20日付け)
具体的に、ヘロン三角形について、その頂点が格子点になるようにできる例を3つあげます。
平行四辺形の面積が外積で求められることに留意しながら、原点を始点とする2本の固定
ベクトルを探します。
始点および2つの終点の3点がヘロン三角形の頂点であるようにはからいます。探す条件
は以下の通りです。
各ベクトルの成分とノルムは整数、2つのベクトルの差の成分とノルムも整数、2本のベク
トルの外積がヘロン三角形の面積の2倍となります。
以下、a、b、c は、ヘロン三角形の辺長、Sは面積とします。
例1 ヘロン三角形(a=30、b=29、c=5 で、S=72)では、
30^2 = 24^2 + 18^2、29^2 = 20^2 + 21^2、5^2 = (24-20)^2 + (18-21)、2*S = 24*21
- 20*18
となる2本の固定ベクトル (24,18)、(20,21) が見つかります。
例2 ヘロン三角形(a=34、b=35、c=15 で、S=252)では、
34^2 = 30^2 + 16^2、35^2 = 21^2 + 28^2、15^2 = (30-21)^2 + (16-28)^2、2*S
= 30*28 - 16*21
となる2本の固定ベクトル (30,16)、(21,28) が見つかります。
例3 ヘロン三角形(a=39、b=34、c=25 で、S=420)では、
39^2 = 36^2 + 15^2、34^2 = 16^2 + 30^2、25^2 = (36-16)^2 + (15-30)^2、2*S
= 36*30 -15*16
となる2本の固定ベクトル (36,15)、(16,30) が見つかります。
# 任意のヘロン三角形について、2本の固有ベクトルがみつかるかどうかは私には不明です。
DD++さんからのコメントです。(平成30年12月22日付け)
これ、ずっと考えているんですが、どこから手をつけたものやら。全て有理数である点に取
れるのは明らかなんですが、それらの分母を1にできる保証をどこから引っ張り出せばよい
のやら。
らすかるさんからのコメントです。(平成30年12月22日付け)
中身は見ていませんが、Webサイト「数学問題」に証明らしきものがありました。
ハンニバル・フォーチュンさんからのコメントです。(平成30年12月24日付け)
難しい証明ですね… 何が効いているのか全く把握できませんでした。頭の中で狐がコーン
とないています。
DD++さんからのコメントです。(平成30年12月25日付け)
なんとか自力で解答にたどり着きました。いきなり証明だとややこしいので、先に構成例を
提示してから実際に証明をします。
例:三辺の長さが 17、65、80 で面積 288 のヘロン三角形の場合
仮の底辺を長さ65の辺とします。
(実は他の2つの方が簡単に済むのですが、説明のためにあえて面倒な辺を使っています)
仮の底辺の両端を O(0,0) と A(65,0) に取ります。三角形の面積が288なので、残り1つの
点Bのy座標は、576/65(ここでは+を採用)で、OB=17、AB=80 とするなら、∠AOBが鈍角な
ので、x座標は、-√(17^2-(576/65)^2)=-943/65 になります。
さて、Bの座標の分母65の素因数を1つ選びます。ここでは、5を選ぶことにしましょう。
5^2=4^2+3^2 なので、arctan(3/4)だけ、点Oを中心に反時計回りまたは時計回りに△OAB
を回転させてやることを考えます。
点B(-943/65,576/65) の移る先は、
(-943/65*4/5-576/65*3/5, -943/65*3/5+576/65*4/5) または
(-943/65*4/5+576/65*3/5, 943/65*3/5+576/65*4/5)
ですが、実は、前者すなわち反時計回りのは綺麗に5^2で約分ができて、B’(-220/13,-21/13)
になります。このとき、点Aは、A’(52,39) に移ります。
再び、B’の座標の分母13の素因数を1つ選びます。13しかないので、これを選ぶことにし
ましょう。
13^2=12^2+5^2 なので、arctan(5/12)だけ、点Oを中心に反時計回りまたは時計回りに
△OA’B’を回転させてやることを考えます。
点B’(-220/13,-21/13) の移る先は、
(-220/13*12/13+21/13*5/13, -220/13*5/13-21/13*12/13) または
(-220/13*12/13-21/13*5/13, 220/13*5/13-21/13*12/13)
ですが、実は、前者すなわち反時計回りのは、綺麗に13^2で約分ができて、B’’(-15,-8) に
なります。このとき、点A’は、A’’(33,56) に移ります。
こうして、三辺の長さが 17、65、80 で面積 288 のヘロン三角形の場合、(0,0)、(-15,8)、
(33,56) という格子点で構成できることがわかりました。
...という、上の例のようなことが常にできる証明が以下。
(証明) 三角形の頂点のうち1つを原点 O(0,0) に、1つをx軸の正の部分 A(a,0) にとりま
す。
aは、この三角形の辺の長さの1つになるので、自然数です。第3の点Bは、辺の長さに合
わせて適当にとります。
∠AOB について、そのcosの値は余弦定理より有理数、そのsinの値も三角形の面積公式
から有理数。
したがって、点Bはx座標もy座標も有理数です。
これらの2乗の和は、自然数の平方になるため、その既約分母はもその分母は、4N+1型
素因数しかもちません。
(分母が2や4N+3型素因数をもつ場合、分母を払った式を見ると実は分子の同じ素因数を
持っていることが示せてしまい、既約であることに矛盾)
ということで、その共通分母をkとおき、B(s/k,t/k) とおきます。sおよびtはいずれもkと互い
に素な整数です。
このとき、OBの長さが整数であることから、s^2+t^2 は k^2 の倍数です。また、三角形の
面積は at/2k と書け、これは自然数になるのでaはkの倍数です。
ここで、kを素因数分解して同種の素因数も分けて k=p1*p2*p3*……*pn とかけたとしま
しょう。今の状況は、「点Aはx座標もy座標も p1*p2*p3*……*pn の倍数である整数、点B
は、x座標もy座標も、分母が、p1*p2*p3*……*pn である有理数」となっています。
さて、p1は、4N+1型素数なので、フェルマーの二平方定理により p1^2=u^2+v^2 となる互い
に素な自然数u、vが存在します。
これを用いて、arctan(v/u)だけ点Oを中心に反時計回りまたは時計回りに△OABを回転
させてやることを考えます。
Bの移る先であるB’のx座標は、 (s/k)*(u/p1)-(t/k)*(±v/p1) のいずれかですが、この2
つ候補の分子同士を掛け合わると、
(su-tv)*(su+tv)=s^2*u^2-t^2*v^2=s^2*(u^2+v^2)-(s^2+t^2)*v^2
であり、右辺は p1^2 の倍数同士の差なので、全体も p1^2 の倍数です。
しかし、suもtvもp1を約数に持たないため、su-tv と su+tv がともにp1の倍数ということは
ありえません。
したがって、これら2つの分子の片方は p1^2 の倍数になっており、つまり、適切な方向の
回転でB’のx座標の分母を、
k/p1=p2*p3*p4*……*pn
にすることができます。
このとき、OB’ が整数であることから、B’のy座標の分母も p2*p3*p4*……*pn になって
いることは明らかです。
また、点Aはx座標もy座標も p1*p2*p3*……*pn の倍数である整数だったので、その移
る先A’はx座標もy座標も p2*p3*p4……*pn の倍数である整数です。
結局、「点A’はx座標もy座標も p2*p3*p4……*pn の倍数である整数、点B’はx座標もy座
標も分母が p2*p3*p4*……*pn である有理数」という状況になりました。
続けて、p2について同様のことを行い、p3について同様のことを行い……とすると、最後に
pnについて同様のことを行ったときに、
「点A’’’……’は、x座標もy座標も1の倍数である整数、点B’’’……’はx座標もy座標も分
母が1である有理数」 すなわち、格子点を結んだ三角形になっています。
この最後にできた三角形は、元々の三角形を繰り返し回転移動させたものなので、元の
ヘロン三角形と合同なものであることは明らかです。
#この証明を書いてみて思ったのですが、頂点を格子点に取れる条件として、「2辺が整数
かつ残りの1つも平方したら整数、面積は整数もしくは半整数」くらいでも十分条件になる
ようですね。逆を考えると格子点三角形でも無理数の辺が2つ以上ある場合は多数存在
するので、まだ必要十分条件にはほど遠そうですが。
ハンニバル・フォーチュン(平成30年12月26日付け)
おお!! 素敵ですね!!!質問をさせてください。以下の部分を少し詳しくご説明頂きた
く存じます。何卒宜しくお願い申しあげます。
(分母が2や4N+3型素因数をもつ場合、分母を払った式を見ると実は分子の同じ素因数を
持っていることが示せてしまい、既約であることに矛盾)
※ふたつの有理数(既約分数)のうち、ひとつの分母が、4N+3型素因数を持っていたとして、
通分して和を取ったときに、結果の分子を素因数分解したらさきほどと同じ4N+3型素因数
が現れて、約分できてしまい、結果として約分後の分母には4N+1型素因数のみが現れる、
といったケースを考えて頭が混乱してしまいました。
DD++さんからのコメントです。(平成30年12月26日付け)
例えば、1/2+3/10 という計算は、足した後に5で約分できません。これは、この計算がたま
たまできなかったのではなく、できないことが必然です。
なぜなら、1/2 を通分して 5/10 としたときに分子が5の倍数になるため、5の倍数ではない
もう片方の分子と足して5の倍数には絶対にならないからです。
足した後に約分されるとすれば、それは両方の分母がもともと持っていた因数であること
が必要です。
実際、この足し算は2で約分できますが、もともと両方の分母が2を因数に持っています。
つまり、Bのx座標^2+Bのy座標^2=OB^2 という式において、右辺が整数すなわち完全に約
分できたということは、左辺の分母は全く同じものでなくてはなりません。
ですから、片方だけがその素因数を持っているという状況自体がありえません。
さて、(a/k)^2+(b/k)^2=c^2 という式があったとして、分母を払って a^2+b^2=(kc)^2 として
みましょう。
4N+3型素数は、「平方数の和がその倍数になるのは元々各平方数がその倍数だった場
合のみ」という性質があります。つまり、kcが4N+3型素因数をもつ場合、aもbも同じ素因数
をもっていたことになってしまい矛盾します。
素因数2についても4で割れば似たようなことが言えるので、結局kcは4N+1型素因数しか
持っていません。
よって、kcの約数であるkも4N+1型素因数しか持たないことになります。
……という説明で、ご理解いただけるでしょうか?
ハンニバル・フォーチュン(平成30年12月27日付け)
スッキリいたしました。有り難うございます。それにしてもテクニカルですね!本質をエグっ
ているようで、ビックリしました。
(追記) 令和4年5月7日付け
上記で話題になった問題(→ 参考)
直角三角形の3辺の長さがすべて整数のとき、面積は偶数である
が、一橋大学(平成2(1990)年)で出題されている。
上記ではいろいろな方の検討があったが、私なりに証明をまとめておきたいと思う。
(証明) 直角三角形の直角をはさむ2辺の長さを a、b とし、斜辺の長さを c とおくと、
三平方の定理より、 a2+b2=c2 が成り立つ。
a、b がともに奇数とすると、a2+b2 すなわち、c2 は偶数となり、よって、c は偶数である。
このとき、c2 は4の倍数となる。
一方、a2+b2 が4の倍数になることはない。これは矛盾である。
よって、a、b の少なくとも一つは偶数である。
・a、b がともに偶数のとき、直角三角形の面積=ab/2 は偶数となる。
・a が偶数、b が奇数としても一般性を失わない。このとき、c は奇数である。
b=2m+1、c=2n+1 (m、n は0以上の整数) と書けるので、
a2=(c+b)(c−b)=4(n+m+1)(n−m)=4(n+m)(n+m+1)−8m(n+m+1)
ここで、(n+m)(n+m+1)は偶数なので、 a2 は8の倍数 となる。
a は偶数なので、 a=2k (kは0以上の整数) と書ける。
よって、 4k2 が8の倍数 なので、k2 は2の倍数 すなわち、 k は2の倍数。
以上から、 a は4の倍数 となる。
したがって、直角三角形の面積=ab/2 は偶数となる。 (証終)
以下、工事中!