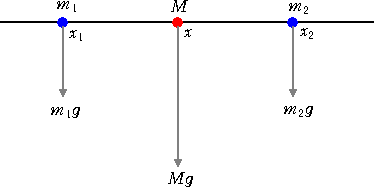
丂暔棟偲偄偆偐椡妛偺暘栰偱丄幙揰宯傗崉懱偺廳怱偑榖戣偵側傞丅偦偺傛偆側抦幆偑偁傞
偲丄悢妛偱廳怱傪峫偊傞応崌偵嬶懱揑僀儊乕僕偑傢偄偰峫偊傗偡偄丅
丂慄暘忋偺俀揰偵偍偄偰丄偦偺廳怱偺埵抲偼偪傚偆偳拞揰偺埵抲偲廳側傞丅偦傟偼丄俀揰偵
摨偠幙検傪晧壸偟偰偄傞応崌偱偁傞偑丄堦斒偵偼師偺傛偆側岞幃偱丄廳怱偺埵抲偼梌偊傜
傟傞丅
丂丂丂
丂忋恾偵偍偄偰椡偺偮傝偁偄偐傜丄丂丂倣1乮倶亅倶1乯亖倣2乮倶2亅倶乯
偙偺幃偼丄悢妛偱峴傢傟傞慄暘偺挿偝偺斾偑
丂丂丂丂丂倶亅倶1丂丗丂倶2亅倶丂亖丂倣2丂丗丂倣1
偱偁傞偙偲傪堄枴偡傞丅偙傟傛傝丄
丂丂丂丂丂丂丂丂丂丂丂
丂悢妛偱偼丄嬒幙側幙揰偲峫偊丄丂倣1亖倣2丂偲偡傞偺偱丄
丂丂丂丂丂丂丂丂丂丂丂
丂偲側傞丅偙傟偼丄惓偟偔崅峑偺乽悢妛嘦乿偱妛傇拞揰偺岞幃偱偁傞丅
丂嶰妏宍偵偍偄偰丄偦偺廳怱偺埵抲偼丄俁拞慄偺岎揰偲偟偰摼傜傟傞丅
丂丂丂丂丂丂丂丂
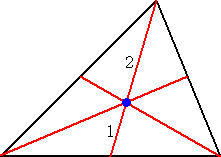
丂廳怱偑拞慄傪 俀丗侾 偵撪暘偡傞偙偲偼丄傛偔抦傜傟偨帠幚偱偁傞丅
丂嶰妏宍偺奺捀揰傪昞偡儀僋僩儖傪丄 倎 丄 倐 丄 們 丂偲偡傟偽丄偦偺廳怱傪昞偡儀僋僩儖偑丄
丂丂丂丂丂丂丂丂丂丂
偱偁傞偙偲偐傜柧傜偐偩傠偆丅
丂偲偙傠偱丄嶰妏宍偺撪怱偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
偱梌偊傜傟傞偑丄倎亖倐亖們丂偡側傢偪丄丂惓嶰妏宍偺偲偒丄撪怱偲廳怱偑堦抳偡傞偙偲偑暘
偐傞丅
丂嶰妏悕偵偍偄偰丄偦偺廳怱偺埵抲偼丄憡懳偡傞曈偺拞揰摨巑傪寢傇慄暘偺拞揰偲偟偰
摼傜傟傞丅
丂偙傟偼丄掙柺偺嶰妏宍偺廳怱偲巆傝偺捀揰傪寢傇慄暘傪 侾丗俁 偵撪暘偡傞揰偱傕偁傞丅
丂丂丂丂丂丂

丂嶰妏悕偺奺捀揰傪昞偡儀僋僩儖傪丄 倎 丄 倐 丄 們 丄 倓丂偲偡傟偽丄偦偺廳怱傪昞偡儀僋僩儖偑丄
丂丂丂丂丂丂丂丂丂丂
偱偁傞偙偲偐傜柧傜偐偩傠偆丅
丂偦傟偱偼丄掙柺偑敿宎 倰 偺墌偱崅偝偑 倛 偺捈墌悕偺廳怱偺埵抲偼偳偆側傞偩傠偆偐丠
摎偼丄嶰妏悕偺応崌偵椶帡偟偰偄偰丄掙柺偐傜偺崅偝偑偪傚偆偳 (侾/係)倛 偺偲偙傠偵偁傞丅
丂偙傟偼丄
丂丂廃偺挿偝偑堦掕側嶰妏宍偱柺愊偑嵟戝側恾宍偼惓嶰妏宍丄廃偺挿偝偑堦掕側
恾宍偱柺愊偑嵟戝側恾宍偼墌偱偁傞
偲偄偆娭學偲椶帡偟偰偄偦偆偱柺敀偄丅
乮捛婰乯丂暯惉俀俆擭俈寧俇擔晅偗
丂壗偲側偔丄敿墌偺廳怱傪媮傔偨偄婥暘偵側偭偨丅僷僢僾僗丒僊儏儖僟儞偺掕棟傪梡偄傟偽
梕堈偵媮傔傜傟傞丅僷僢僾僗丒僊儏儖僟儞乮Pappus-Guldin乯偺掕棟偲巹偺弌夛偄偼丄崅峑俀
擭偺偲偒偱偁傞丅嶲峫彂偵丄夞揮懱偺懱愊偵偮偄偰偼丄師偺掕棟偑惉傝棫偮偙偲偑抦傜傟
偰偄傞偲丄偝傜傝偲婰弎偝傟偰偄傞偵夁偓側偐偭偨偑丏丏丏丅
丂暯柺忋偺暵偠偨慄偱埻傑傟偨恾宍偑丄偙偺暯柺忋偵偁偭偰丄偙傟偲岎傢傜側偄捈慄偺廃
傝偵夞揮偟偰摼傜傟傞棫懱偺懱愊偵偮偄偰丄
丂丂乮棫懱偺懱愊乯亖乮恾宍偺柺愊乯亊乮恾宍偺廳怱偺昤偔墌廃偺挿偝乯
偑惉傝棫偮丅
丂尨揰拞怱偱敿宎 倰 偺忋敿墌傪 倶 幉偺廃傝偵夞揮偝偣傞偲媴偑偱偒傞偺偱丄掕棟傛傝丄
丂丂丂係兾倰3/俁亖兾倰2/俀亊俴丂丂偐傜丄丂俴亖俉倰/俁
丂倷 幉忋偺揰乮侽丆倷乯偵廳怱偑偁傞偺偱丄丂俀兾倷亖俉倰/俁丂偐傜丄丂倷亖係倰/乮俁兾乯
丂偙偺 倷 偺寁嶼偼丄師偺傛偆偵捈愙揑偵傕媮傔傜傟傞丅
丂尨揰拞怱偱敿宎 倰 偺忋敿墌偺曽掱幃偼丄丂倶2亄倷2亖倰2丂乮倷亞侽乯
丂偙偺忋敿墌傪枾搙乮亖兿乯堦條側恾宍偲峫偊傞偲丄偦偺幙検偼丄兾倰2兿/俀
丂嬫娫乵侽丆倰乶傪値摍暘偟丄旝彫側挿曽宍偺柺愊偐傜掕傑傞幙検乮倰/値乯兿併乮倰2亅乮倠/値乯2乯偑
慡偰廳怱偺埵抲乮侾/俀乯併乮倰2亅乮倠/値乯2乯偵偐偐偭偰偔傞偲偡傞偲丄偦偺儌乕儊儞僩偺嬌尷偼丄
丂俀亊倢倝倣値仺亣儼倠=0乣値-1乮倰/乮俀値乯乯兿倗乮倰2亅乮倠/値乯2乯亖兿倗佺0倰乮倰2亅倶2乯倓倶亖俀倰3兿倗/俁
乮偨偩偟丄倗偼廳椡壛懍搙乯
丂傛偭偰丄倷 幉忋偺揰乮侽丆倷乯偵廳怱偑偁傞偲偟偰丄
丂丂俀倰3兿倗/俁亖倷亊兾倰2兿倗/俀
偑惉傝棫偮丅偙偺偲偒丄丂倷亖係倰/乮俁兾乯丂偲側傞丅
丂忋婰偱偼丄暔棟揑偵寁嶼偟偨偺偩偑丄戝妛弶擭媺偱妛傇廳愊暘傪梡偄傟偽傑偨堘偭偨夝
朄偲側傠偆丅
丂敿墌偺廃偍傛傃撪晹傪昞偡椞堟俢丗 倶2亄倷2亝侾丄倷亞侽 偵偮偄偰丄偦偺廳怱偺埵抲偼丄
丂丂倶亖佺D 倶倓倶倓倷/佺D倓倶倓倷丂丄倷亖佺D 倷倓倶倓倷/佺D倓倶倓倷
偱媮傔傜傟傞丅
丂曄悢曄姺丂倶亖倰們倧倱兤丄倷亖倰倱倝値兤丂乮0亝倰亝侾丄侽亝兤亝兾乯偵傛傝丄丂倓倶倓倷亖倰倓倰倓兤
側偺偱丄
丂丂丂佺D 倶倓倶倓倷亖佺01倰2倓倰佺0兾們倧倱兤倓兤亖侽
丂丂丂佺D 倷倓倶倓倷亖佺01倰2倓倰佺0兾倱倝値兤倓兤亖俀/俁
丂丂丂佺D倓倶倓倷亖佺01倰倓倰佺0兾倓兤亖兾/俀
丂傛偭偰丄丂倶亖侽丂丄倷亖係/乮俁兾乯丂傛傝丄廳怱偺嵗昗偼丄丂乮侽丆係/乮俁兾乯乯
丂忋婰榖戣偵偮偄偰丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽埥傞闉偡偲乿偝傫偐傜忣曬傪
捀偄偨丅埥傞闉偡偲偝傫偵姶幱偟傑偡丅乮暯惉俀俆擭俈寧侾俆擔晅偗乯
丂廳怱寛掕偼寢嬊偼愊暘偺栤戣偵婣拝偝傟傞偺偱偡偑丄旝愊暘敪尒埲慜偐傜屄暿偺恾宍
偵娭偟偰偺尋媶偼偝傟偰偄偨傛偆偱偡丅乮仺丂嶲峫丗乽墌偲媴偺媮愊乮捈姶揑曽朄乯乿乯
丂傾儖僉儊僨僗偺敿墌偺廳怱寛掕偑偁傑傝偵傕僄儗僈儞僩偱偡偺偱丄偛徯夘偄偨偟傑偡丅
丂倶倷暯柺偵揰乮亅侾丆侾乯丄乮亅侾丆亅侾乯丄乮侽丆侽乯傪捀揰偲偡傞嶰妏宍偲扨埵墌傪敿暘偵偟偨敿
墌傪峫偊傑偡丅
丂丂丂丂丂丂丂丂丂丂丂
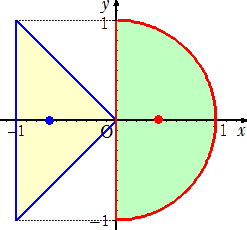
丂偡傞偲丄嶰妏宍偲敿墌偼倶幉傪揤攭偺榬栘丄尨揰傪巟揰偲偟偰偮傝崌偆偲偄偆傕偺偱偡丅偡傞
偲丄嶰妏宍偺廳怱偼揰乮亅俀/俁丆侽乯偺埵抲偵偁傝丄柺愊偺斾偼丄敿墌丗嶰妏宍亖兾/俀 丗 侾丄
偝傜偵丄丂丂乮巟揰偐傜嶰妏宍偺廳怱傑偱偺挿偝乯亊乮嶰妏宍偺柺愊乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖乮巟揰偐傜敿墌偺廳怱傑偱偺挿偝乯亊乮敿墌偺柺愊乯
偐傜丄丂乮俀/俁乯亊侾亖倗亊乮兾/俀乯丂傛傝丄丂倗亖係/(俁兾)
偱偁傞偺偱丄敿墌偺廳怱偼丄揰乮係/(俁兾)丆侽乯偺埵抲偵偁傞偲偄偆傕偺偱偡丅
丂傾儖僉儊僨僗偼丄奺恾宍傪 倶 幉偵暯峴側捈慄偱愗偭偨愗傝岥偑丄廳偝傪帩偮偲壖掕偟偰丄
偦傟傜柍尷偺愗傝岥偑偡傋偰丄巟揰偵懳偟偰偮傝崌偆偲偄偆偙偲傪崻嫆偵偦傟傜慄暘傪廤傔
偨乮柍尷偵乯恾宍傕偮傝偁偆偼偢偩偲偄偆丄偁傞庬偺岞棟傪慜採偟偰偄傑偡丅
丂恾側偟偱偼偦偺偮傝崌偄偺媍榑傪峴偄偵偔偄偺偱丄嶲峫恾彂傪偁偘偰偍偒傑偡丅
侾丂T.L.Heath丂塸栿丂乽俿he method of Archimedes乿丂pp38乣40丂proposition12
俀丂椦塰帯丂嵵摗寷丂挊乽揤攭偺杺弍巘丂傾儖僉儊僨僗偺悢妛乿pp173乣178丂柦戣13
丂侾偵偮偄偰偼丄僼儕乕偺PDF偑岞奐偝傟偰偄傑偡丅側偍丄挊幰偵傛傝丄柦戣偺斣崋晅偑堎側
傝傑偡偺偱偛拲堄偔偩偝偄丅
丂敿墌偺廳怱寛掕偺愊暘寁嶼偼偦傟側傝偵暋嶨偱偡偑丄怴偨側媄朄傪惗傑側偔偲傕婛懚偺
媄朄偱夝偗傞栤戣偼夝偄偰傗傞偲偄偆惁傒偲丄偦偺僄儗僈儞僩側撪梕偑傾儖僉儊僨僗偺尋媶
惉壥偺側偐偱傕嵺棫偭偰偄傞柦戣偲巚偄傑偡丅
丂場傒偵丄傾儖僉儊僨僗偵偼丄敿墌偺廳怱寛掕偼丄偄傢備傞崌奧乮捈岎岎嵎墌拰懱乯偺
懱愊寛掕偺偨傔偺弨旛偩偭偨傛偆偱偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俆擭俈寧侾俇擔晅偗乯
丂徯夘偺暥專傪撉傒丄棟夝偟傑偟偨丅愜妏側偺偱悢幃揑偵彂偔偙偲傪帋傒偰偍偒傑偡丅
曗戣丂俀偮偺慄暘 A亝y亝B 偲 C亝y亝D 偑丄倶亖侽偱乽掁傝崌偆乿
丂丂丂丂佁丂乮B2亅A2乯亄乮D2亅C2乯亖侽
丂幚嵺偵丄侾偮栚偺慄暘偺廳怱偼丄乮A亄B乯/俀 偱偁傝丄廳偝偼丄乮B亅A乯倠
丂俀偮栚偺慄暘偺廳怱偼丄乮C亄D乯/俀 偱偁傝丄廳偝偼丄乮D亅C乯倠
丂乽掁傝崌偆乿偲偄偆偙偲偼丄偦傟傜偺愊偺榓偑0偱偁傞丅
丂乮B亅A乯倠丒乮A亄B乯/俀亄乮D亅C乯倠丒乮C亄D乯/俀亖侽
丂偡側傢偪丄丂乮B2亅A2乯亄乮D2亅C2乯亖侽
丂偝偰丄杮戣偱偡丅嶰妏宍傪丄 亅侾亝倷亝 亅|倶|丂丄敿墌傪丄 侽亝倷亝併乮侾亅倶2乯丂偱帵偡丅
倶嵗昗傪屌掕偟偰愗傝庢傜傟偨慄暘傪峫偊傞偲丄愭偺曗戣偵帵偟偨娭學幃傪枮偨偡偙偲偑暘
偐偭偨乮媄岻揑両乯丅
丂幚嵺偵丄捈慄 倶亖倲 乮侽亝倲亝侾乯 偱愗傝庢傜傟偨嶰妏宍偺曽偺慄暘俙俛偵偮偄偰丄
丂丂丂丂俙乮倲丆亅侾乯丂丄俛乮倲丆亅倲乯丂傛傝丄丂乮B2亅A2乯亖倲2亅侾
丂捈慄 倶亖倲 乮倲亞侽乯 偱愗傝庢傜傟偨敿墌偺曽偺慄暘俠俢偵偮偄偰丄
丂丂丂丂俠乮倲丆侽乯丂丄俢乮倲丆併乮侾亅倲2乯乯丂傛傝丄丂乮D2亅C2乯亖侾亅倲2
丂偟偨偑偭偰丄丂乮B2亅A2乯亄乮D2亅C2乯亖乮倲2亅侾乯亄乮侾亅倲2乯亖侽
乮僐儊儞僩乯丂嵟弶丄乮B2亅A2乯亖乮D2亅C2乯偱偼丠偲巚偭偨偺偱偡偑丄幚嵺偵忋婰偺傛偆偵寁
丂丂丂丂丂丂嶼偟偰傒傞偲丄乮B2亅A2乯亄乮D2亅C2乯亖侽丂側傫偱偡偹両
乮捛婰乯丂廳怱偺幚尡偵偮偄偰丄俧俙俬 偝傫偐傜偺搳峞偱偡丅乮暯惉俀俆擭俋寧侾侾擔晅偗乯
丂擟堄偺嶰妏宍偺廳怱俧偺埵抲偼丄偍側偠傒偺奺拞慄偺岎揰偱敪尒偝傟傞丅偙偺揰偼岤巻
偱偙偺嶰妏宍傪嶌偭偰丄偦偺揰偵嵶偄朹傪摉偰傞偲僶儔儞僗傛偔掁傝崌偆丅傑偨丄奺捀揰偵摨
偠廳偝乮椺偊偽侾侽墌乯傪掁傝壓偘偰傕丄偦偙偺揰偼曄偊側偔偰傕傛偄丅
丂堦曽丄擟堄偺巐妏宍傪岤巻偱偮偔傝丄偳偙偱掁傝崌偆偐傪扵偡曽朄偼丄岦偐偄崌偆捀揰傪偦
傟偧傟寢傃丄係偮偵暘偐傟傞嶰妏宍乮帪寁傑傢傝偵俙丆俛丆俠丆俢偲柤晅偗傞乯傪俀偮偢偮慻傒
崌傢偣傞乮俙丆俛堦懱偲俠丆俢堦懱傕偟偔偼俛丆俠堦懱偲俙丆俢堦懱乯偙偲偱偱偒傞嶰妏宍傪峫偊偰丄
偦傟偧傟偺嶰妏宍偵偱偒傞廳怱俧侾丄俧俀丄傕偟偔偼俧俁丆俧係傪嶌恾偱尒偮偗弌偟丄俧侾丄俧俀傪
寢傇慄暘偲俧俁丆俧係傪寢傇慄暘傪堷偄偰丄偦偺岎揰偑僶儔儞僗傪偲傟傞埵抲偲偟偰敪尒偝傟
傞丅
丂偲偙傠偑丄偙偺埵抲偼奺捀揰偵侾侽墌嬍傪掁傝壓偘偰傒傞偲僶儔儞僗偑曵傟丄嶰妏宍偺傛偆
偵摨偠揰偲偟偰懚嵼偱偒側偔側傞丅乮岤巻偵傛傞幚尡偱偺尰徾傛傝乯
丂側偍丄偙偪傜偺揰偼丄捀揰偐傜俆侽侽墌嬍傪巺偱偮傞偟丄捀揰傪帩偭偰巐妏宍傪帩偭偨偲偒巺
偑悅傟傞慄傪俀僇強偺捀揰偱幚尡偟偰俀杮偺慄偑岎傢傞揰偲偟偰敪尒偱偒傞丅
丂偙偺傛偆偵廳怱偲偄偆奣擮偼巐妏宍埲忋偺宍忬偱偼擇捠傝峫偊傜傟傞偺偱偼偲巚偄傑偟偨丅
偙傟傜偺偙偲偵娭偡傞堄尒傪暦偐偣偰壓偝偄丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俆擭俋寧侾侾擔晅偗乯
丂巐妏宍偺捀揰偵廫墌嬍傪捿傝壓偘偨傕偺偺廳怱偼丄乽巐妏宍偺廳怱乿偲偼尵傢側偄乮娭學
側偄乯偲巚偄傑偡丅
丂傕傕偭偙偆偺晝偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俆擭俋寧侾侾擔晅偗乯
丂墯巐妏宍偺拞偵偼丄廳怱偑撪晹偵側偄傕偺偑偁傞偺偱乧丅係暘妱傕柍棟偱偡偟乧丅係暘妱
偝傟偨嶰妏宍偺柺愊偑偽傜偽傜側偺偱丄埵抲儀僋僩儖偱昞偟偨傜丄偳偆偱偟傚偆偐丠俀暘妱偟偨
嶰妏宍偺廳怱傪寢傇慄暘忋偱峫偊側偄偲丄怴偨側係揰偑尰傟傞偺偱丄崲傝傑偣傫偐偹偊丠
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭俀寧俁擔晅偗乯
丂巹偼暔棟宯弌恎偱偡偺偱丄暔懱偺廳怱 g 偲偄偊偽師偺幃傪巚偄晜偐傋傑偡丅
丂丂g=(佺V x兿(x)dx)/(佺V 兿(x)dx)丂丂傑偨偼丂丂g=(儼[i]m[i]x[i])/(儼[i]m[i])
乮仸m[i]傗x[i]偼m,x偵壓晅偒揧偊帤i偺偮傕傝偱偡丅m_i偲偐x_i偲偐彂偒偨偄偗偳傑偓傢傜偟偔側
傞偟丄偳偆偟偨傕偺偐乧丅乯
丂偙偙偱丄V偼暔懱偺愯傔傞嬻娫丄兿(x)偼暔懱偺枾搙丄m[i]丄x[i]偼暔懱偺i斣栚晹暘偺幙検丄
埵抲偱偡丅
丂Wikipedia偺廳怱偺儁乕僕偵偍偄偰偼丄枾搙偑f(x)偱偁傞恾宍D偵懳偟偰丄佺D (g-x)f(x)dx=0
傪枮偨偡揰g傪廳怱偲掕媊偟偰偄傑偡丅偙傟傪曄宍偡傞偲丄g=(佺D xf(x)dx)/(佺D f(x)dx)丂偲側
偭偰丄嵟弶偵帵偟偨椡妛偵偍偗傞幃偲堦抳偟偰偄傑偡丅
丂悢妛揑偵偼丄枾搙f(x)偑constant偺応崌傪媍榑偡傞偙偲偑傎偲傫偳偱偟傚偆丅偡側傢偪丄
丂丂佺D (g-x)dx=0丂丂偁傞偄偼丄幃曄宍偡傟偽丄丂g=(佺D xdx)/(佺D dx)
偲側傝傑偡丅偝偰丄偙偺掕媊偺傕偲偱丄GAI偝傫偺搳峞偵懳偡傞堄尒傪弎傋傛偆偲巚偄傑偡丅
丂偦偺慜偵丄GAI偝傫偺擇偮偺幚尡傪幃偱昞偟偰傒偨偄偲巚偄傑偡丅擮偺偨傔弎傋偰偍偒傑
偡偑丄埲壓偱x偼俀師尦嵗昗偱偡丅
丂傑偢丄巐妏宍偺岤巻偺傒乮廫墌嬍側偟乯偺幚尡傪幃偱昞偟傑偡丅岤巻偺柺枾搙傪r(x)丄岤
巻偺幙検傪倣偲偍偔偲丄丂倣=佺D r(x)dx丂偲側傝傑偡丅廳怱偺埵抲g偼丄
丂丂g=(佺D xr(x)dx)/(佺D r(x)dx) =(佺D xr(x)dx)/倣
偱偡丅岤巻偺柺枾搙偑堦掕偱偁傞偲傒側偣傞側傜偽丄偙偺g偼悢妛揑側廳怱偲堦抳偟傑偡丅
偦傟偵懳偟偰丄捀揰偵廫墌嬍傪捿傝壓偘偨応崌偺幚尡偵偮偄偰幃偵彂偒壓偟偰傒傑偡丅
丂4偮偺捀揰偺埵抲儀僋僩儖傪a丄b丄c丄d偲偍偒傑偡丅廫墌嬍偺幙検傪M偲偍偗偽丄岤巻偲
廫墌嬍傪偁傢偣偨慡懱偺柺枾搙f(x)偼丄
丂丂f(x)=r(x)+M兟(x-a)+M兟(x-b)+M兟(x-c)+M兟(x-d)
偲側傝傑偡丅偙偙偱兟(x)偼乮曄悢偑俀師尦偺乯僨傿儔僢僋偺兟娭悢偱偡丅岤巻偲廫墌嬍傪崌傢
偣偨宯偺廳怱偺埵抲g'偼丄
g'=(佺D xf(x)dx)/(佺D f(x)dx)
=(佺D xr(x)dx+M佺D x兟(x-a)dx+M佺D x兟(x-b)dx+M佺D x兟(x-c)dx+M佺D x兟(x-d)dx)
丂丂/(佺D r(x)dx+M佺D 兟(x-a)dx+M佺D 兟(x-b)dx+M佺D 兟(x-c)dx+M佺D 兟(x-d)dx)
=(mg+Ma+Mb+Mc+Md)/(m+M+M+M+M)
=(mg+M(a+b+c+d))/(m+4M)
偲側傝傑偡丅傕偟丄岤巻偺幙検偑廫墌嬍偺幙検偵斾傋偰廫暘偵彫偝偔乮m<<M乯丄柍帇偱偒傞偺
側傜偽(m/M<<1)丄
丂丂g'=((m/M)g+a+b+c+d)/(m/M+4)佮(a+b+c+d)/4
偲側傝傑偡丅偙偺偲偒丄g'偼4捀揰偺嵗昗傪嶼弍暯嬒偟偨嵗昗偺揰偵側偭偰偄傞偲偄偊傑偡丅
丂偝偰丄偙偙偐傜巹偺堄尒偱偡丅
丂捠忢乽巐妏宍偺廳怱乿偲偄偆偲偒偼丄掕媊偵偍偗傞恾宍D偵乮撪晹傑偱娷傔偨俀師尦恾宍偲偟
偰偺乯巐妏宍傪偁偰偼傔偰偄傞偲峫偊傜傟傑偡丅
丂偦偟偰丄係偮偺嶰妏宍偵暘偗偰媮傔傞傗傝曽偱偁傟偽丄惓偟偔偙偺乽巐妏宍偺廳怱乿傪媮傔傞
偙偲偑偱偒傑偡丅
丂墯巐妏宍偺応崌偵傕乮巐妏宍偺奜懁偱傕嶌恾偑偱偒傞偲偄偆慜採偱乯摨偠傛偆側傗傝曽偱媮
傔傜傟傑偡丅
丂巐妏宍偺岤巻偺傒偺幚尡偱偼丄岤巻偺柺枾搙偑堦掕側傜偙偺廳怱偺埵抲偱掁傝崌偆偱偟
傚偆丅偟偐偟廫墌嬍偁傝偺幚尡偱掁傝崌偆揰偼偙偺堄枴偱偺乽巐妏宍偺廳怱乿偲偼屇傋側偄偲
巚偄傑偡丅
丂廳怱偲偄偆尵梩傪巊偆偲偟偨傜丄岤巻偺廳偝偑柍帇偱偒傞応崌偵乽暯柺忋偵偁傞乮摍偟偄廳
傒傪帩偮乯係揰偺廳怱乿偲偱傕偄偆傋偒偱偟傚偆丅
丂偲偙傠偱丄GAI偝傫偑偳偆偟偰偙偺傛偆偵峫偊偨偺偐偼嶰妏宍偺応崌偺摿庩側帠忣偵婲場偟
偰偄傞傛偆偱偡丅
丂嶰妏宍偺応崌丄巹偑弎傋偨掕媊偐傜媮傔偨廳怱偲丄俁偮偺捀揰嵗昗傪嶼弍暯嬒偟偨揰偑
堦抳偟傑偡丅
乮俀師尦嬻娫偺嶰妏宍偺応崌偵尷傜偢丄堦斒偵n師尦嬻娫偱偼n師尦扨懱偱摨條偺偙偲偑帵
偣傑偡丅乯
丂偙偺帠幚偐傜丄嶰妏宍側傜偽廫墌嬍傪捿傝壓偘偰傕掁傝崌偆揰偼曄傢傜側偄偲偄偆偙偲偵側
傝傑偡丅偙偺嶰妏宍偵偍偗傞尰徾傪巐妏宍偵傕揔梡偟傛偆偲偟偰偟傑偭偨偺偱偼側偄偐偲巚偄
傑偟偨丅
丂嶰妏宍偺廳怱偑g=(a+b+c)/3偱昞偝傟傞偙偲偼桳柤偱偡偑丄偙傟偼嶰妏宍偺応崌偵尷偭
偰摫偐傟傞傕偺偱偁傞偲巚偭偰偄偨傎偆偑偄偄偲巚偄傑偡丅
乮傕偭偲偄偆側傜丄扨懱偱偼捀揰嵗昗傪嶼弍暯嬒偟偨揰偑廳怱偲堦抳偡傞偑丄堦斒偺恾宍偱
偼偦偆側傞偲偼尷傜側偄偲偄偆偙偲偱偡丅乯
丂悢妛偺儁乕僕側偺偵敿暘暔棟傒偨偄側榖戣偵側偭偰偟傑偄傑偟偨丅
乮捛婰乯丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽埥傞闉偡偲乿偝傫偐傜乽傾儖僉儊僨僗偺敿墌
丂丂丂丂偺廳怱寛掕栤戣乿偵偮偄偰曗懌傪偄偨偩偒傑偟偨丅乮暯惉俀俉擭俈寧俀係擔晅偗乯
丂栺俁擭慜偵傾儖僉儊僨僗偺敿墌偺廳怱寛掕偵偮偄偰搳峞偟偨偺偱偡偑丄偙偪傜偺僒僀僩偼
悢妛宯丠偺僽儘僌側偳偵堷梡偝傟傞偙偲傕懡偄傛偆偱丄偦偺嵺丄岆夝偝傟偰偄傞晹暘偑偁傞
傛偆偱偡偺偱丄曗懌偟偨偄偲巚偄傑偡丅
丂傑偨壞媥傒婜娫偲偄偆偙偲傕偁傝丄堄梸揑側拞妛惗偺嶲峫偵傕側傞傛偆偵丄娭悢傪巊傢偢丄
恾宍偺栤戣偲偟偰丄偛徯夘偟傑偡丅

