円と球の求積（直感的方法）

円と球の求積（直感的方法）　　　　　　　　　　　　　　

　正方形や長方形などの面積の公式は、誰でもが納得しやすい。なぜなら、面積の概念そ
のものが、単位正方形が何個あるかによって決まるからで、そこは疑いようがないところで
あろう。

　平行四辺形や台形、ひし形の面積の公式も、その延長線上にあり、比較的容易である。

　しかしながら、円の面積はまだしも、球の体積、球の表面積の公式となると、その直感的
な把握は難しいようである。

　私の周囲の方々に伺っても、「そんなの、鵜呑みにして覚えて、計算したよ～」という場合
が多い。私自身、最初にどうやって教えられたのか、もう忘れてしまっているのだが、以前
にＮＨＫ教育テレビで、円柱と円錐と球の模型を水槽に沈めて、その押しのけた水の量で
球の体積の公式を説明していたのを見たような気がする。

　このページでは、円や球という図形に的を絞って、その面積や体積・表面積の公式を、直
感的に求める方法について整理しておきたい。

　出発点は、まず円周率である。円周率は、直径に対する円周の比で定義される。数学の
場合、直径というものはあまり使用頻度の高い語彙ではなく、むしろ、半径と絡めた方が本
質的かもしれない。（ →　参考「円の面積」）

　したがって、円の半径をｒ、円周率を π とすると、円周の長さは、

　　　　　　（円周の長さ）　＝　２ π ｒ

という公式により求められる。これは、円周率の定義そのものなので、疑う余地は全くない。

　小学校４年で、円や球の概念を学習するわけであるが、あくまでも「見た目」の形の理解
に重きが置かれる。この頃は、円の持っている美しい対称性と、自然に触れ合うことが大
切で、妙に心引かれるものを感じるときでもあろう。

　小学校５年で、扇形や中心角、円周率などの用語が登場し、円の面積の公式を語るため
の役者が勢ぞろいする。曖昧さを上手くカバーしながら、巧妙に、平行四辺形の面積もしく
は長方形の面積を用いて、円の面積が求められる。分かりやすさに重きを置くので、論理
の微妙な部分は反古にされる。小学校でのこのような対応は、むしろ教育的なのだろう。

　　左図のような半径ｒ　　
　の円を、右図のように　　
　細かく扇形に等分割
　する。　　　
　　　　　　　　　　

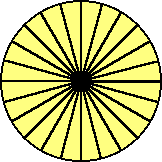　等分割されたものを、上下に２分割し、下図のようにかみ合せる。

	⇒
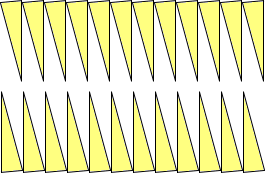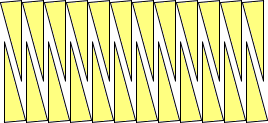そうすると、教室の遠くからは、あたかも長方形かのように見える図形ができる。

　　「横がちょっとデコボコでは～？」という質問があった場合は、すかさず「今は、分割数
が少なくて、そう見えるかもしれないが、この分割数をどんどん増やしていくと、だんだんと
滑らかになります。」と説明すれば、恐らく多くの小学生には納得してもらえることと思う。

　厳密に言えば、あやふやだが、円の面積というものを既知の図形に変換することにより、
具体的に体感できる方法としては、優れた指導法だと思う。（多分おおくの小学校では、こ
のようなやり方で教えられているはずである。）

　この長方形の縦の長さは、円の半径ｒに等しく、横の長さは、半円周の長さ π ｒに等し
いので、

　　　　　　（円の面積）　＝　π ｒ²

という公式が作られる。

　円の面積公式の、厳密な意味での証明は、三角関数の微分積分を待たなければならな
い。しかし、この証明に出会える日本の高校生は、現行のカリキュラムでは非常に少ない。
（恐らく、日本の高校３年生の１割位ではないだろうか？）

　学習指導要領で、球の体積や表面積の公式は高校１年で学ぶ「数学Ⅰ」の「図形と計量」
に強制移動させられてしまったが、平成２４年度から始まった新学習指導要領では、また、
中学校数学に差し戻しにされた。（旧学習指導要領では中学３年だが、もっと昔は、中学１年で教
えられていた！）　

　円や球は、その全方位的な対称性から、長方形や直方体にはない図形の美しさが感じら
れる対象である。数学的なものの見方・考え方を養成するには格好の対象だと思う。その
反省から中学校数学に復活したのだろう。

　円の面積の場合は、円周の長さが既に定まっていたので、容易に直感的な求積法を導
くことができたが、球の場合は、少し事情が異なる。足がかりとなり得る球の表面積、体積
の何れもが定められていないからである。

　しかし、そのどちらかを与えれば、次の直感的な方法により、他方は定まる。

　　　半径ｒの球において、中心から放射状に、左図のよう
　　なコーンを考える。（図では、１個しかないが、これが球面
　　上密集しているような図を想像して下さい．．．　f(^_^)　）

　　　このコーンの高さは、ｒに等しいとしてよい。

　　　このとき、球の表面積Ｓと体積Ｖには、次の等式

　　　　　　　Ｖ＝(1/3)・Ｓ・ｒ

　　が成り立つ。

　一般的に、表面積を直感的方法で求めることは、難しい。
（球の表面積が、球に外接する円柱の側面積に等しいことが言えればよい。）

　それに対して、体積の方は、

カヴァリエリ（Cavalieri）の原理

　　２つの立体を、平行な平面で切ったときの切り口の面積がいつも等しければ、２つの立
　体の体積は等しい。

という、直感的に受け入れやすい原理があるので、説明しやすい。

　カヴァリエリの原理を用いると、底面積と高さが同一である、円錐と角錘の体積は等しい
ことが分かる。また、角錐の体積が、角柱の体積の３分の１であることは、当ＨＰ：「角錐の
体積」により、理解されることだろう。

　球の表面積Ｓと体積Ｖの関係式で、「３分の１」が乗ぜられるのは、この「３分の１」であ
る。

　カヴァリエリの原理を用いて、球の体積は、次のようにして求められる。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（当ＨＰ：「カヴァリエリの原理」より再掲）
　下図において、

　　　　「半径ｒの半球」
　　と、
　　　　「半径ｒ、高さｒの円柱から半径ｒ、高さｒの円錐を取り除いた立体」

　　のそれぞれの体積は等しい。
　　　　　　　　　　　　球の体積　　　

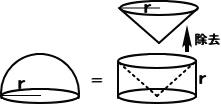
　　　実際に、それぞれの立体を、底面に平行な
　　平面（点線）で切断したときの断面積は、２つ
　　とも
　　　　　　　　　π (ｒ^２－Ｘ^２)
　　に等しい。

　　従って、球の体積は、　２×（πｒ³－（1/3)πｒ³）＝(4/3) π ｒ³

以上から、

　　　　　　（球の体積）　＝　(4/3) π ｒ³
という公式が作られる。

　解析的には、高校３年で学ぶ「数学ＩＩＩ」の微分積分において、円の回転体の体積として、
球の体積の公式は求められる。（←以前は高校２年で学ぶ「数学ＩＩ」の内容であった。）

　ところで、半径、高さがともにｒの円錐、半球、円柱の体積の比が、１：２：３ になる
という事実は、とても美しい。

　さらに、半径、高さがともにｒの円柱、円錐、球、の体積の比が、３：１：４ になるが、
何となく、円周率３．１４と意味ありげで、興味深い。

　球の体積の公式から、表面積Ｓは、　(4/3) π ｒ³ ＝ (1/3)・Ｓ・ｒ　より、Ｓ＝ ４ π ｒ²

以上から、

　　　　　　（球の表面積）　＝　４ π ｒ²

という公式が作られる。

　球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。

　　　　　　球の体積　は、　身の上に心配あるので、参上。

　　　　　　球の表面積は、心配ある事情。

上記以外の直感的方法がないかどうか、今後の研究課題としたい。

　当ＨＰ読者のＨＮ「或る髷すと」さんからのコメントです。（平成２５年８月１８日付け）

　アルキメデスの文献（The method of Archimedes）のｐ．18～ｐ．21の命題２も、議論は複
雑な部分もありますが、積分を用いないため、カウ゛ァリエリの原理と同様に、直感的な方法
と言えるのではないかと考えます。

　アルキメデスの求積は、例えば、半径ｒの円の面積は、πｒ² ではないと矛盾するというよ
うに、全て背理法により証明が行われているため、予め結果を知っておく必要がありました。
そこで、the method of Archimedesにあるような仮想の天秤を用いたようです。

（コメント）　或る髷すとさんに感謝します。

　或る髷すとさんからのコメントです。（平成２５年８月２５日付け）

　アルキメデスの「Ｔhe method of Archimedes」の仮想天秤について、少し解説じみたことを
試みます。

　アルキメデスの論文には、数式や比の考え、次元の異なる量の加減乗除が無いため、少
し理解しにくいと思うので、下記の議論が理解の助けになればと思います。是非、古代ギリ
シャの数学を味わってみて下さい。

　y＝x² の放物線がｘ軸と作る図形の 0≦x≦1 における面積を仮想天秤で求めます。つま
り、∫₀^１x²dx　を求めます。

　原点を天秤の支点とし、天秤の横木を　-1≦x≦1　におけるｘ軸とします。y＝ｘが 0≦ｘ≦1
で作る三角形を考え、放物線と三角形を点X（ｘ，0）でｘ軸に垂直な線分で切り取ると、切り口
の長さは、
　　　　　　　（放物線の切り口）：（三角形の切り口）＝ｘ² ：ｘ＝ｘ： 1
となります。

　そこで、　(点Xから支点までの長さ) ：（点A(-1，0)から支点までの長さ)＝ｘ： 1

ですので、放物線の切り口の線分を点Aにつるすと、三角形の切り口の線分とそのままの位
置で釣り合います。図形は切り口の線分が無限に集まったものと考えると、そのままの位置
にある三角形と、点Aでつるした放物線が作る図形は釣り合います。

　三角形の重心は点（2/3，0）にあるので、三角形を重心につるすと、

　　　　（三角形の面積）：（放物線が作る図形の面積）＝３：２

となり、三角形の面積は、1/２から、放物線が作る図形の面積は、１/３となります。

　よって、∫₀^１x²dx＝１/３　が証明されました。

　さて、以上が仮想天秤の概要ですが、もう少し検討してみます。この方法では、x^ｎの定積
分を求めるのに、xⁿ－１の図形の重心が既知でなければなりません。xⁿ－１の重心を決
定するには、結局、xⁿ の定積分を計算しなければならないため、重心が既知である図形を
用いた特殊な場合に使用は制限されます。ですから、カウ゛ァリエリの原理や積分法の様な
汎用性は勿論ありませんが、味わいのある手法と思います。

　アルキメデスは仮想天秤を用いて、放物線、球、楕円球、回転放物線体、回転双曲線体、
交差円柱、円柱の切片の求積を行っています。全て二次式の積分の問題に帰着されます。
しかし、半円の重心決定の様な、二次式の積分に帰着されない問題も仮想天秤を用いて
解決しています。（→　参考：「重心の位置」）

　現代の我々は仮想天秤を用いて、上記以外の図形の求積を行えるのでしょうか。何か面
白い結果がありましたら、お知らせ下さい。

（コメント）　仮想天秤という考え方、面白いですね！∫₀^１x²dx＝１/３　の証明に感動しまし
　　　　　　た。このような機会を与えていただいた、或る髷すとさんに感謝します。

　りんごさんから球の体積に関する問題をいただきました。（平成２８年７月３日付け）

　内のりが２cmの立方体である容器に水が高さ１cmまで入っている。この容器に直径が
１．２cmの球を底まで沈めたとき、水面の高さは何cm上昇するか？

　DD++さんが考察されました。（平成２８年７月３日付け）

　球の体積は、(４/３)×π×０．６³＝０．２８８π cm³ です。ここで、「もし仮に球が水面より

下に完全に沈むなら」、体積０．２８８π cm³ の球を沈めるのと体積０．２８８π cm³ の水

を加えるので水面は同じだけ上昇するはず。

　加えたのが水なら、2×2×h＝０．２８８π から h＝０．０７２π cm 水面は上昇することに

なります。つまり、「もし仮に球が水面より下に完全に沈むなら」、球の場合も答えは、

０．０７２π cm が答えです。

　あとは、「本当に球が水面より下に完全に沈むのか？」ですが、π＝３．１４としてみると、

０．０７２π＝０．２２６０８なので、水の深さはおよそ１．２２６ cm で、直径１．２ cm の球は

ぎりぎり沈みきっています。よって、答えは、０．０７２π cm です。

＃もし最後の確認で「実は水面より下に完全には沈んでいなかった」となった場合には、ど
　れくらい水面からはみ出るのかの計算を改めて行うことになります。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（高校３年～大学レベル）

　りんごさんからのコメントです。（平成２８年７月３日付け）

　すみません、内のりは３cmで、半径が１．２cmの球でした。積分の計算をがんばるしかな
いのですね……。

　DD++さんからのコメントです。（平成２８年７月３日付け）

　直径１．２cmだとやけにピッタリなので、そういう中学生の問題かと思ったら違ったんですね。

　積分を真面目に頑張ってもいいですが、手抜きをしてもいいですね。つまり、「半径ｒの半球
を伏せたものの高さhまでの体積は、半径r高さhの直円柱から半径h高さhの直円錐を引いた
ものに等しい」のを利用して、上半分を計算し、下半分は普通に半球で計算する、と。
（「　」の事実は直円錐を上下逆さまにして水平断面積を考えれば明らかです。）

　しかしこれ、三次方程式になりそうな．．．。最悪カルダノの公式でなんとかできますが……。

　らすかるさんからのコメントです。（平成２８年７月３日付け）

　実際に解いてみたところ、答えは、

　　3〔{20π√(160π³-1175π²+2500π)+64π³-100π²}^1/3
　　-{20π√(160π³-1175π²+2500π)-64π³+100π²}^1/3〕/(10π)
　　+1/5(cm)
　(≒0.592282639033661939753256077584…)

となりました。３次方程式を解いて答えを整理する手間と比べたら、積分の手間は（真面目
にやりましたが）誤差レベルでした。