����̘a�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�E�P ���� �� �܂ł̎��R���̘a �F �P�{�Q�{�E�E�E�{�� �����i���{�P�j/�Q
�E�P ���� �� �܂ł̎��R���̕����̘a �F �P2�{�Q2�{�E�E�E�{��2 �����i���{�P�j�i�Q���{�P�j/�U
�E�P ���� �� �܂ł̎��R���̗����̘a �F �P3�{�Q3�{�E�E�E�{��3 ����2�i���{�P�j2/�S
�@��L�̘a�̌����́A���Z�Ŋw�ԁA�悭�m��ꂽ�����ł���B�������A���̏ؖ��́A�P����
���g���ȂǁA���܂�ɑ㐔�I�Ŗ��C�Ȃ��B���̃y�[�W�ł́A�����ƒ����I�ɕ�����₷���A��
�̂���ؖ��ɂ��Ă܂Ƃ߂����Ǝv���B�܂��́A���ȏ��̋L�q�K���Ă݂悤�B
�P ���� �� �܂ł̎��R���̘a
�@���ȏ��ł́A�P�����@ (���{�P�j2�|��2 ���Q���{�P�@�𗘗p���āA�� �ɂP�C�Q�C�R�C�E�E�E�C���@��
������ċ��߂�̂����ʂł���B
�@�@�� �̎���ӁX�����āA�@(���{�P)2�|�P ���Q( �P�{�Q�{�R�{�E�E�E�{�� )�{��
�@����āA�@�Q( �P�{�Q�{�R�{�E�E�E�{�� )��(���{�P)2�|(���{�P)����(���{�P)
�@�@���̎����A��L�̌�����B
�i�NjL�j�@�ߘa���N�U���P�V���t��
�@�P�����@ (���{�P�j2�|��2 ���Q���{�P�@��ӁX�������ɁA���̂悤�ȓ��������m���Ă���B
�@��k=1n {(���{�P�j2�|��2} ����k=1n (���{�P�j2�|��k=1n ��2��(���{�P)2�|�P����2�{�Q��
����āA�@�Q��k=1n ���{������2�{�Q���@���A�@��k=1n ������(���{�P)/�Q
�P ���� �� �܂ł̎��R���̕����̘a
�@���ȏ��ł́A�P���� (���{�P�j3�|��3 ���R��2�{�R���{�P �𗘗p���āA�� �ɂP�C�Q�C�R�C�E�E�E�C��
�������ċ��߂�̂����ʂł���B
�@�� �̎���ӁX�����āA
�@(���{�P)3�|�P ���R(�P2�{�Q2�{�R2�{�E�E�E�{��2)�{�R( �P�{�Q�{�R�{�E�E�E�{�� )�{��
����āA
�R(�P2�{�Q2�{�R2�{�E�E�E�{��2)
��(���{�P)3�|�R�~���i���{�P�j/�Q�|(���{�P)�����i���{�P�j�i�Q���{�P�j/�Q
�@���̎����A��L�̌�����B
�i�NjL�j�@�ߘa���N�U���P�V���t��
�@�P�����@(���{�P�j3�|��3 ���R��2�{�R���{�P ��ӁX�������ɁA���̂悤�ȓ��������m���Ă�
��B
�@��k=1n {(���{�P�j3�|��3} ����k=1n (���{�P�j3�|��k=1n ��3��(���{�P)3�|�P
����āA�@�R��k=1n ��2�{�R��(���{�P)/�Q�{����(���{�P)3�|�P�@���A
�R��k=1n ��2
��(���{�P)3�|�R��(���{�P)/�Q�|���|�P
��{(���{�P)/�Q}{�Q(���{�P)2�|�R���|�Q}
��{(���{�P)/�Q}{�Q��2�{��}
�����i���{�P�j�i�Q���{�P�j/�Q
�@����āA�@��k=1n ��2�����i���{�P�j�i�Q���{�P�j/�U
�i�NjL�j�@�ߘa�R�N�P�O���P�R���t��
�@��L�̏ؖ�����Ԃ悭�m���Ă���Ǝv���邪�A�Q���W���́u���a�̌����v��p������
�����a�V�ŋ����[���B
�i�NjL�j�@�ߘa�R�N�X���V���t��
�@�����F�P2�{�Q2�{�E�E�E�{��2 �����i���{�P�j�i�Q���{�P�j/�U�@�̊o�����ɂ��āA
�@�P2�{�Q2�{�E�E�E�{��2 �����i���{�O�D�T�j�i���{�P�j/�R
�Ƃ������������Ƃ����ӌ�������B������O�D�T���݂ɑ����Ă����āA�R�Ŋ���Ƃ������߂Ȃ�
�����A�F����͂��������납�H
��@�P2�{�Q2�{�E�E�E�{�Q�O2 ���Q�O�~�Q�O�D�T�~�Q�P/�R���S�P�O�~�V���Q�W�V�O
�i�R�����g�j�@���̔��z�����������ʂ͂ǂ�Ȃ��낤�H
�P ���� �� �܂ł̎��R���̗����̘a
�@���ȏ��ł́A�P�����@ (���{�P�j4�|��4 ���S��3�{�U��2�{�S���{�P�@�𗘗p���āA�� ��
�P�C�Q�C�R�C�E�E�E�C���@�������ċ��߂�̂����ʂł���B
�@���̌v�Z��܂Ƃߕ��̃R�c�́A�������̏ꍇ�ƑS�������Ȃ̂ŁA�����ł́A���̋L�q����
�����邱�Ƃɂ���B
�@���̂P ���� �� �܂ł̎��R���̗��@�̘a���A�P ���� �� �܂ł̎��R���̘a �m ��p���āA
�@�P3�{�Q3�{�R3�{�E�E�E�{��3 ���m2
�Ə�����Ƃ������Ƃ́A�����g���Z����ɕs�v�c�Ɏv���������ł���B
�@���̂��Ƃɂ��āA���g�o�����������b�ɂȂ��Ă���r�i�g�j����̏��i�����Q�P�N�U��
�Q�X���t���j�ɂ��ƁA
�@�t���� ���܂�� �i�����������@�e�����������������@�i1580�`1635�j���A���̒�
�@�`���������������@�`�������������@�i�P�U�R�P�j
�ɂ����āA�@�P5�{�Q5�{�R5�{�E�E�E�{��5 ��(�S�m3�|�m2�j/�R
���̌����i�P17�{�Q17�{�R17�{�E�E�E�{��17 �܂ł̊�p�ɂ��āj���q�ׂĂ���Ƃ����B
�@��ʂ̏ꍇ�ɂ��ẮA�P�W�R�S�N�ɁA�i���������� ���ؖ������炵���B
�@�P5�{�Q5�{�R5�{�E�E�E�{��5�@�����߂Ă݂悤�B
�@�܂��A�P�����@ (���{�P�j5�|��5 ���T��4�{�P�O��3�{�P�O��2�{�T���{�P�@�𗘗p���āA
�@(���{�P�j5�|�P5 ���T����4�{�P�O����3�{�P�O����2�{�T�����{���P
������A�@����4�����i���{�P�j�i�Q���{�P�j�i�R��2�{�R���|�P�j/�R�O
�@�܂��A�P�����@ (���{�P�j6�|��6 ���U��5�{�P�T��4�{�Q�O��3�{�P�T��2�{�U���{�P�@�𗘗p���āA
�@(���{�P�j6�|�P6 ���U����5�{�P�T����4�{�Q�O����3�{�P�T����2�{�U�����{���P
������A�@����5����2�i���{�P�j2�i�Q��2�{�Q���|�P�j/�P�Q
�@����āA�@���i���{�P�j���Q�m�@��������A
�@�P5�{�Q5�{�R5�{�E�E�E�{��5���S�m2�i�S�m�|�P�j/�P�Q��(�S�m3�|�m2�j/�R
�ł��邱�Ƃ������ꂽ�B
��@�P5�{�Q5�{�R5�{�E�E�E�{�P�O5�@���v�Z����B
�i���j�@�m���T�T�@�Ȃ̂ŁA
�@�@�@(�S�m3�|�m2�j/�R���m2�i�S�m�|�P�j/�R���R�O�Q�T�E�Q�P�X/�R���R�O�Q�T�E�V�R���Q�Q�O�W�Q�T
�@�@���A�@�P5�{�Q5�{�R5�{�E�E�E�{�P�O5���Q�Q�O�W�Q�T�@�ł���B�@�i�I�j
�i�R�����g�j�@��r�I�ȒP�ɋ��߂��܂��ˁI
�@�A�����鐮���̐ς̌`�ŁA����a�̌��������߂���@������B�i���@�Q�l�j
�@���̂悤�Ȑ���̘a�̌����ɑ���ʉ��Ƃ��Đ��Ԉ�ʂł́A�Q�r�@�Ƃ��R�r�@�A�S�r�@
�Ȃǂ̕��@���Љ��Ă���B�i���̕��@�ɂ����E�����邱�Ƃ��������番����ł��낤�B�j
�Q�r�@�E�E�E�P ���� �� �܂ł̎��R���̘a
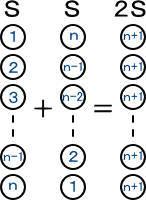 |
�@�@�@�@���}��薾�炩�ɁA�Q�r���i���{�P�j���������i���{�P�j�@������
�@�@�@�����A�����ɁA�����邱�Ƃ��ł���B
�@�@�@�@���̂悤�Ȍv�Z���@�́A�K�E�X�ɂ���ĂȂ��ꂽ�ƌ�����
�@�@�@����B
�@�@�@�@�K�E�X�����w���̎��A�S���̐搶���u�P����P�O�O�܂ł̘a�v
�@�@�@���v�Z����Ƃ��������o���āA���炭���Ԃ������邾�낤
�@�@�@�Ǝv���Ă����Ƃ���A�K�E�X�������ǂ���ɁA���̕��@�ʼn�����
�@�@�@���܂����Ƃ�����b���L���ł���B
|
�R�r�@�E�E�E�P ���� �� �܂ł̎��R���̕����̘a
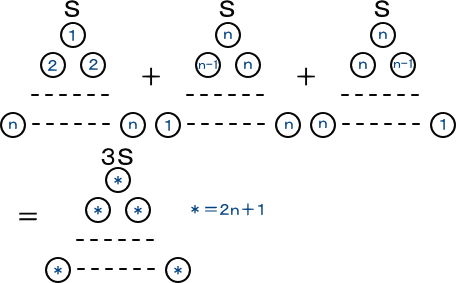
�@��L�̌v�Z�ɂ����āA�e�O�p�`�̏ォ�炋�i�ځA�����炍��ڂ̐������߂Ă݂�ƁA��
�ꂼ��@���@�A���|���{���@�A���|���{�P �Ȃ̂ŁA���̘a�́A�Q���{�P�@�ƂȂ�B
�@���������āA��}��薾�炩�ɁA�R�r���i�Q���{�P���P�{�Q�{�E�E�E�{�������i���{�P�j/�Q �j�@����
�藧���A�����Ɍ����邱�Ƃ��ł���B
�����R���̕����̘a�̌����́A���łɁA�A���L���f�X�i�I���O�Q�W�V�H�`�Q�P�Q�j���m���Ă�
�@���ƌ����Ă���B
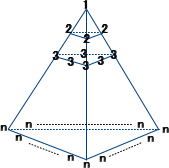
�S�r�@�E�E�E�P ���� �� �܂ł̎��R���̗����̘a
�@�S�r�@�́A�Q�r�@�A�R�r�@�Ɠ��l�Ȕ��z�ł��邪�A��L�̕��@�Ɣ�ׂĔώG�Ȍv�Z��������
�ꂸ�A�G���K���g���Ɍ�����̂ŁA�Љ�́A���炷�������ɂƂǂ߂����B
�@��{�I�ɂ́A�r�f���P�{�Q�i�P�{�Q�j�{�R�i�P�{�Q�{�R�j�{�E�E�E�{���i�P�{�Q�{�E�E�E�{���j�@���v�Z����
�킯�ł��邪�A���̂悤�ȗ��̂��S�p����B�p�����́A�R�r�@�Ɠ��l�ł���B
�@��̓_�ɒ��ڂ���ƁA�a�͂��ׂā@�R���{�P�@�ł��邱�Ƃɒ��ӂ���B
�@�@�@
�P ���� �� �܂ł̎��R���̗����̘a
�@�����̘a�̌v�Z�ɂ��āA���͔�������@���m���Ă���B�����m���Ă���a�̌v�Z��
���ł��A���̔������͌Q���Ă���B����́A�Q����ɂ���@�ł���B
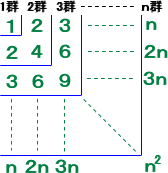 |
�@�@���}�̂悤�ɁA���R����@�P�A�Q�A�E�E�E�A���@���A�Q�{�A�R�{�A�E�E�E
�@�������̂��A���̍s�ɏ��������Ă����A���ŋ��A�Q����
�@�����B���}�ɂ�����鎩�R���̑��a�́A���炩�ɁA
�@�@�@�@�i�P�{�Q�{�R�{�E�E�E�{���j2����2�i���{�P�j2/�S
�@�@�����ŁA�悋�Q�ɓ����Ă��鎩�R���̘a�����߂�ƁA
�@�@�i�P�{�Q�{�E�E�E�{���j���{�i�P�{�Q�{�E�E�E�{���j���|��2����3�@�ł���B |
�@�@�@�@�@�@�@�@�@�@�@�]���āA��P�Q����悎�Q�܂ł̘a�����߂邱�Ƃɂ��A�����͎������B
�i�ʉ��j�@�@�P ���� �� �܂ł̎��R���̗����̘a�ɂ��āA���̂悤�ȌQ�����p�����@��
�@�@�@�@�@�@�m������B
�i�Q�l�����F���q���M�@���@�ׂ���a����x���k�[�C���C�[�[�^������
�@�@�i���w�Z�~�i�[�@�f�O�R�N�P�O�����j�@�i���{�]�_�Ёj�j
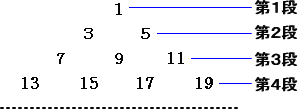 |
�@�@�@�P ����n�܂���̏�������� ��
�@�@���܂ł̘a�́A��2 �ŗ^������B
�@�@�@�� �� �i�ɂ́A�� �̊���܂܂��
�@�@�̂ŁA��P�i����� �� �i�܂łɊ܂܂��
�@�@��̑����́A
�@�@�@�P�{�Q�{�R�{�E�E�E�{�� �����i���{�P�j/�Q |
�@���������āA��P�i����� �� �i�܂łɊ܂܂���̑��a�́A�@��2�i���{�P�j2/�S
�@�Ƃ���ŁA�� �� �i�́A������ ��2�|���{�P�A������ ��2�{���|�P�A������ �� �̓�������ł�
�邩��A���̘a�́A�ȒP�Ȍv�Z����A��3 �ƂȂ�B
�@���������āA�@�P3�{�Q3�{�R3�{�E�E�E�{��3 ����2�i���{�P�j2/�S�@�@�i�I�j
�P ���� �� �܂ł̎��R���̕����̘a�i���C�v�j�b�c�̕��@�j
�@�����̘a�̌v�Z�ɂ��āA�K������𗘗p������@���m���Ă���B���̕��@�́A���C
�v�j�b�c�����������ƌ����Ă���B
| ��0 |
��1 |
��2 |
��3 |
�E�E�E |
| �@ |
��1 |
��2 |
��3 |
�E�E�E |
| �@ |
�@ |
��2 |
��3 |
�E�E�E |
| �@ |
�@ |
�@ |
��3 |
�E�E�E |
| �@ |
�@ |
�@ |
�@ |
�E�E�E |
|
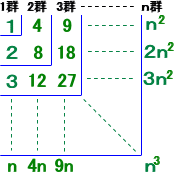
�@�@���}�ɂ����āA
�@�@�@�@�@�����������|����-1�A�����������|����-1�A�E�E�E
�@�@�@�ł���B
�@�@���̂Ƃ��A���Ƃ��A�@�@ |
�@��3����2�{��3���i��1�{��2�j�{�i��2�{��3�j����1�{�Q��2�{��3�@�E�E�E�E�E�i*�j
�@���i��0�{��1�j�{�Q�i��1�{��2�j�{�i��2�{��3�j����0�{�R��1�{�R��2�{��3�@�E�E�E�E�E�i**�j
�@���̂��Ƃ���A��3�@�̒l�́A�Ίp���̐������狁�߂��邱�Ƃ�������B����ɁA���̊e��
�̌W���́A���̍�����A��3�@�֍s���ŒZ�o�H�̐��ɓ������B
�@���Ƃ��A��1�@����@��3�@�֍s���ɂ́A���ɂQ�}�X�A�c�ɂP�}�X�i�߂悢����A���̕��@��
���́A����E�g�����̗��_�ɂ��A3�b1 ���R�i�ʂ�j�ł���B
�@��̌v�Z�ŁA�i*�j�i**�j�̂Ƃ����m���߂ė~�����Ǝv���B
�藝�i���C�v�j�b�c�j
�@�@������n�b0��0�{n�b1��1�{n�b2��2�{n�b3��3�{�E�E�E
�@���ۂɁA���R���̕����̘a�̌v�Z�ɉ��p���Ă݂悤�B
| �O |
�P |
�T |
�P�S |
�R�O |
�T�T |
�E�E�E |
| �@ |
�P |
�S |
�X |
�P�U |
�Q�T |
�E�E�E |
| �@ |
�@ |
�R |
�T |
�V |
�X |
�E�E�E |
| �@ |
�@ |
�@ |
�Q |
�Q |
�Q |
�E�E�E |
| �@ |
�@ |
�@ |
�@ |
�O |
�O |
�E�E�E |
|
�@�@���}�ɂ����āA��P�s�́A
�@�@�������P2�{�Q2�{�R2�{�E�E�E�{��2
�@�ŗ^�����鐔��ł���A��Q�s�ȉ��́A���̊K�������
�@����B�������A��0���O�@�Ƃ���B |
���̂Ƃ��A��T�s�ȉ��́A�S�ĂO�ł��邱�Ƃɒ��ڂ���B�@�藝�ɂ��A
�@������n�b0�~�O�{n�b1�~�P�{n�b2�~�R�{n�b3�~�Q
�ƂȂ�A������v�Z���邱�Ƃɂ��A�����邱�Ƃ��ł���B
�i�Q�l�����F���R�@�[�@���@���w����i��g�V���j
�@�@�@�@�@�@�@�v�ۋG�v�@���@����Ƌ����i�Ȋw�V���Ёj�j
�@�i�@���@����̘a�̋��ߕ��ŏd�S�̊T�O�𗘗p�������@�ɂ��ẮA�u�M�u�X�̎O�p�`�v���Q���j
�i�NjL�j�P ���� �� �܂ł̎��R���̂S��̘a
�@�S��̘a�̌v�Z�ɂ��āA�����̘a�Ɠ��l�ɁA�Q�����p������@������B
 |
�@�@���}�̂悤�ɁA����@�P�A�S�A�X�A�E�E�E�A��2�@���A�Q�{�A�R�{�A�E�E�E
�@ �������̂��A���̍s�ɏ��������Ă����A���ŋ��A�Q����
�@�����B
�@�@���}�ɂ�����鐔��̑��a�́A���炩�ɁA
�@�@
�@�@�i�P�{�Q�{�R�{�E�E�E�{���j�i�P2�{�Q2�{�R2�{�E�E�E�{��2�j
�@����2�i���{�P�j2�i�Q���{�P�j/�P�Q
�@�����ŁA�悋�Q�ɓ����Ă��鎩�R���̘a�����߂�ƁA |
�@�i�P�{�Q�{�E�E�E�{���j��2�{�i�P2�{�Q2�{�E�E�E�{��2�j���|��3���i�T/�U�j��4�{�i�P/�U�j��2
���������āA��P�Q����悎�Q�܂ł̘a�����߂邱�Ƃɂ��A���߂�a�� �r �Ƃ���ƁA
�@�i�T/�U�j�r�{���i���{�P�j�i�Q���{�P�j/�R�U����2�i���{�P�j2�i�Q���{�P�j/�P�Q
����āA�@�r�����i���{�P�j�i�Q���{�P�j�i�R��2�{�R���|�P�j/�R�O
�i�Q�l�����F�����`��E��粌b��@���@�㐔��}�`�ʼn����i�u�k�Ѓu���[�o�b�N�X�j�j
�i�NjL�j�@��L�ł́A�@�r��(��)���P���{�Q���{�R���{�E�E�E�{�����@�̘a�̌����̂��낢��ȋ��ߕ�
�@�@�@�@�@���݂Ă����B
�@�r1(��)���P�{�Q�{�R�{�E�E�E�{������(���{�P)/�Q��(�P/�Q)��2�{(�P/�Q)��
�@�r2(��)���P2�{�Q2�{�R2�{�E�E�E�{��2����(���{�P)(�Q���{�P)/�U��(�P/�R)��3�{(�P/�Q)��2�{(�P/�U)��
�@�r3(��)���P3�{�Q3�{�R3�{�E�E�E�{��3����2(���{�P)2/�S��(�P/�S)��4�{(�P/�Q)��3�{(�P/�S)��2
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@���̂悤�Ȏ����ڂ���ƒ��߂Ă���ƁA
�@�r3�f(��)����3�{(�R/�Q)��2�{(�P/�Q)�����R�E�r2(��)�@�@�i�`���I�ɁA�� �Ŕ����I�j
�Ƃ����W�������藧���ƂɋC�Â��B���̂悤�ȊW�́A
�@���a �� �̉~�̖ʐ� �r����2 ���A�� �Ŕ�������ƁA�r�f���Q�� �́A���a �� �̉~���̒�����
�\��
�@���a �� �̋��̑̐� �u��(�S/�R)��3 ���A�� �Ŕ�������ƁA�u�f���S��2 �́A���a �� �̋��̕\
�ʐς�\��
�Ɏ��Ă���B�i�����̊W�����Z����ɋC�Â����Ƃ��ɂ́A�ƂĂ����������I�j
�@���́A���̂悤�ȊW�́A��ʓI�ɐ�������炵���B���N�炳�A�Q�O�O�S�N�X������
���w�Z�~�i�[�i���{�]�_�Ёj�̒��́A�u�G���K���g�ȉ����Ƃށv�ɏo�肳��Ă���B
�i�́A�P�Q�������Q�Ɓj
�@�@� �� �ɑ��āA�@�rk�f(��)�����E�r��-1(��)�@�@�i�`���I�ɁA�� �Ŕ����I�j
�u�� �͊�v�Ƃ���������������邪�A�ƂĂ��������W�ł���I
�i�⑫�j�@�����P�X�N�W���P�R���t��
�@��L�̌������ؖ��������肪�A�����P�W�N�x������w ��������@���w�ɏo�肳��
���B�i�ꕔ�\�����C���j
������w����i�Q�O�O�U�j
�@���A�� �����R���Ƃ���B���̖₢�ɓ�����B
�i�P�j�@���{�P �������� �r���i���j�������āA
�@�@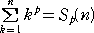
�ƕ\����邱�Ƃ������B
�i�Q�j�@�� �����R���Ƃ���B�i�P�j�̑����� �r1�i���j�A�r3�i���j�A�E�E�E�A�r2q-1�i���j�ɑ��āA
�@�@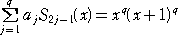
���P�����ƂȂ�悤�Ȓ萔 ��1�A�E�E�E�A���� �� �� ��p���ĕ\���B
�i�R�j�@�� ���Q�ȏ�̎��R���Ƃ���B�i�P�j�̑����� �r2�i���j�A�r4�i���j�A�E�E�E�A�r2q-2�i���j�ɑ��āA
�@�@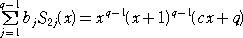
���P�����ƂȂ�悤�Ȓ萔 �� �� ��1�A�E�E�E�A����-1 �� �� ��p���ĕ\���B
�i�S�j�@�� ���R�ȏ�̊�Ƃ���B���̂Ƃ��A
�@�@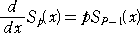
�������B
�i�����j�@�i�P�j�́A���w�I�A�[�@��p����B���ȏ��ł�������Ă����@
�@�i���{�P�jp+1�|��p+1 �̓W�J���� �����P�A�Q�A�E�E�E�A���@�ɂ��Ęa���Ƃ�
���Ƃɂ��A�e�ՂɎ������B
�i�Q�j���A�@�e�i���j����q�i���{�P�jq �ɑ��āA�e�i���j�|�e�i���|�P�j �̓W�J�����@�����P�A�Q�A�E�E�E�A��
�ɂ��Ęa���Ƃ邱�Ƃɂ�莦�����B
�@�i���{�P�j/�Q���������@�̂Ƃ��A�@�������Qq�b2q-2j+1
�@��L�ȊO�̂Ƃ��A�@�������O
�i�R�j��������ς����A�p�����@�́i�P�j�i�Q�j�Ɠ����ł���B�@�r2���i���j�|�r2���i���|�P�j����2��
�ɒ��ӂ��Čv�Z���邱�Ƃɂ��A�@�����Q���@�ł��邱�Ƃ�������B���̂Ƃ��A
�@�@�f�i���j����q-1�i���{�P�jq-1�i�Q�����{���j �ɑ��āA�f�i���j�|�f�i���|�P�j �̓W�J����
�����P�A�Q�A�E�E�E�A���@�ɂ��Ęa���Ƃ邱�Ƃɂ�莦�����B
�@�i���|�P�j/�Q���������|�P�@�̂Ƃ��A�@�������Q�i�Q���{�P�jq�b2q-2j-1
�@��L�ȊO�̂Ƃ��A�@�������O
�i�S�j�́A���w�I�A�[�@��p����B�O�q�Ŏ������悤�Ɂ@�r3�f(��)���R�E�r2(��)�@�����藧�̂ŁA
�@�����R�@�̂Ƃ��A�^����ꂽ����͐��藧�B�Q���|�P �����̊ �� �ɂ��āA
�@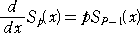
�����藧���̂Ƃ���B�����Q���|�P�@�̂Ƃ��A�@�����R �Ȃ̂ŁA�@�����Q
�@�i�Q�j�ŋ��߂�ꂽ�P�����@��1�r1�i���j�{��2�r3�i���j�{�E�E�E�{��q�r2q-1�i���j����q�i���{�P�jq
�ɂ����āA�@�����Q�@�Ȃ̂ŁA�@��1���O�@�ł���B��2�r3�i���j�{�E�E�E�{��q�r2q-1�i���j����q�i���{�P�jq
�̗��ӂ�������āA
��2�E�R�r2�i���j�{�E�E�E�{��q-1�E�i�Q���|�R�j�r2q-4�i���j�{��q�r2q-1�f�i���j������q-1�i���{�P�jq-1�i�Q���{�P�j
�@�i�Q�j�i�R�j�́@���� �A �����@�̊W����A
�@��1�r2�i���j�{�E�E�E�{��q-2�r2q-4�i���j�{��q�r2q-1�f�i���j����q-1�i���{�P�jq-1�i�Q�����{���j
�����藧�B�i�R�j�̍P�����Ɣ�r���āA�@��q�r2q-1�f�i���j����q-1�r2q-2�i���j
�@�����ŁA�@�������Qq�b1���Q���@�A�@����-1���Q�i�Q���|�P�jq�b1���Q���i�Q���|�P�j�@�Ȃ̂ŁA
�@�r2q-1�f�i���j���i�Q���|�P�j�r2q-2�i���j�@�����藧�B
����āA�����Q���|�P�@�̂Ƃ�������͐��藧�B
�@���������āA�R�ȏ�̊ �� �ɑ��āA
�@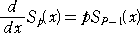
�����藧�B�i�I�j
�i�R�����g�j�@�����P�U�N�X���ɏo�ł���āA�����P�W�N�x�����ɏo��Ƃ������Ƃ��l����ƁA��
�@�@�@�@�@�@���o��҂͐��w�Z�~�i�[�̖����ӎ����Ă����̂��ȁH����Ƃ��Ɨ��ɍl����
�@�@�@�@�@�@�ꂽ���Ȃ̂��ȁH
�@����ɂ��Ă��A���̖������ԓ��ɉ������Ƃ͂قڍ���Ƃ������Ƃ͌�����B�R��P�T�O��
�̎��������A���ɂ͐h���o�肾�I
�i�NjL�j�@�����P�V�N�V���Q�T���t���ŁA�_�ސ쌧�� �r ����Ƃ���������A
�@������̎��A�@�rk�f(��)�����E�r��-1(��)�@�����藧���A�������ʉ����āA�r��(��)
����@�r���{�P(��)�@�����߂���@���l���܂���
�Ƃ������[���Ղ����B�r ���A���̘b��ɂ��āA���錤����Ɍf�ڂ��ꂽ���e��
PDF�t�@�C�����Q�l�ɂ����Ă����������B�r ����ɑ�ϊ��ӂ������܂��B
�@�r ���l����ꂽ���@�͎��̂悤�Ȃ��̂ł���B
�i�P�j�@�r���|�P(��) �ɑ��āA���ӂ� �� �{����B�i�ō����̌W�����P�ɂȂ�悤�ɂ���j
�i�Q�j�@�i�P�j�œ���ꂽ���̂��A �� �Ɋւ��Č`���I�ɐϕ�����B�ϕ��萔�́A�O
�Ƃ���B
�i�R�j�@�e���̌W���̘a�� �P �ɂȂ�悤�ɁA�K�X �P ���̍���t��������B
�@���̑���ɂ��A�r��(��) ��������B
��@�@�r1(��) �� (�P/�Q)��2�{(�P/�Q)���@�A�r2(��) �� (�P/�R)��3�{(�P/�Q)��2�{(�P/�U)�� �ł��邪�A
�@�r2(��) �́A�r1(��) ���玟�̂悤�ɂ��ē�����B
�@�܂��A�i�P�j ����A�@�Q�E�r1(��) �� ��2�{���@�ŁA�@�i�Q�j����A(�P/�R)��3�{(�P/�Q)��2
�@�P�|�o(�P/�R)�{(�P/�Q)�p���P/�U�@�Ȃ̂ŁA�@�i�R�j����A(�P/�U)�� ��t�������āA
�@�r2(��) �� (�P/�R)��3�{(�P/�Q)��2�{(�P/�U)���@�@�i�@���@�҂������J���J���I�I�j
��@�@�r2(��) �� (�P/�R)��3�{(�P/�Q)��2�{(�P/�U)�� �@�A�r3(��) �� (�P/�S)��4�{(�P/�Q)��3�{(�P/�S)��2
�ł��邪�A�r3(��) �́A�r2(��) ���玟�̂悤�ɂ��ē�����B
�@�܂��A�i�P�j ����A�@�R�E�r2(��) �� ��3�{(�R/�Q)��2�{(�P/�Q)���@�ŁA�i�Q�j����A
�@(�P/�S)��4�{(�P/�Q)��3�{(�P/�S)��2
�@�P�|�o(�P/�S)�{(�P/�Q)�{(�P/�S)�p���O�@�Ȃ̂ŁA�@�i�R�j�ŁA�t�������鍀�͂Ȃ��B
�@����āA�@�@�r3(��) �� (�P/�S)��4�{(�P/�Q)��3�{(�P/�S)��2�@�@�i�@���@�҂������J���J���I�I�j
�i�R�����g�j�@�� ����̎��A�rk�f(��)�����E�r��-1(��) �����藧�̂ŁA���Ƃ��A�����R�@�̂Ƃ��A
�@�r3�f(��)���R�E�r2(��)�@�����藧�B�@�r2(��) �� (�P/�R)��3�{(�P/�Q)��2�{(�P/�U)���@�Ȃ̂ŁA
�@�r3�f(��) �� ��3�{(�R/�Q)��2�{(�P/�Q)���@�ƂȂ邪�A���ӂ�ϕ����āA
�@�r3(��) �� (�P/�S)��4�{(�P/�Q)��3�{(�P/�S)��2�{�b�@�i�b �͐ϕ��萔�j
�@�����ŁA�r3(�P) �� �P�@�Ȃ̂ŁA�@�b���O�@�łȂ���Ȃ�Ȃ��B
�@����āA�@�r3(��) �� (�P/�S)��4�{(�P/�Q)��3�{(�P/�S)��2
�@���̂悤�ɁA�� ����̎��́A�s��ϕ��Ə��������i�H�j �r��(�P) �� �P �Ƃ�����������A
�r��(��) �����肷�邱�Ƃ��ł��邪�A�� �������̎��́A��L�̂悤�ȑQ���������݂��Ȃ���
�ŁA�ϕ��� �r��(��) �����肷�邱�Ƃ͖������낤�ƒ��߂Ă����B����A�r ����̑N�₩�ȕ�
�@�i���ɁA�i�R�j�I�j�ɑ傫�Ȋ������o���܂����B
�@�����ŁA�r ����̕��@��������Ă������Ǝv���B
�@�r��(��)���P���{�Q���{�R���{ �E�E�E �{�����@�ɂ����āA�@
�@�r��(��)�|�r��(���|�P) �� �����@�A�@�r��(�P) �� �P
�Ƃ����W�����{���I�ł���B
�@ �㎮�́A �� �̍P�����Ȃ̂ŁA�㎮�ɂ��A �� �̑����� �r��(��) �͈�ӓI�Ɍ��肳���B
�@�Ƃ���ŁA�� �̑����� �r��(��) �͓������鐫���������Ă���B
�㎮�ɂ����āA�@�����P�@�Ƃ����Ă݂�ƁA�@�r��(�P)�|�r��(�O) �� �P�@�ŁA�r��(�P)���P�@����A
�r��(�O)���O�@�����藧�Ƃ���̂����R���낤�B
�@����́A�r��(��) ���萔���������Ȃ����Ƃ��Ӗ�����B
�@���Ȃ킿�A�r��(��) �́A�� �Ŋ�����B
����ɁA�����O�@�Ƃ����Ă݂�ƁA�@�r��(�O)�|�r��(�|�P) �� �O�@�ŁA�r��(�O)���O�@����A
�r��(�|�P)���O�@�����藧�Ƃ���̂����R���낤�B
�@����́A�r��(��) ���A���{�P �Ŋ����邱�Ƃ��Ӗ�����B
���������āA�C�ӂ� �� �ɑ��āA�r��(��) �́A���i���{�P�j �ŕK��������B
�@�Ƃ���ŁA��L�̊W�����`���I�� �� �Ŕ�������ƁA
�@�r���f(��)�|�r���f(���|�P) �� ���E�����|�P�@�@���A�@�r���f(��)/���|�r���f(���|�P)/�� �� �����|�P
�@���̂Ƃ��A�@�r���f(��)/�� ���A�r���|�P(��) �Ɖ��炩�̊W�����邱�Ƃ͏�q�̂��Ƃ���\�z
�����B
�@�����ŁA�����P�@�̂Ƃ��A�r���f(�P)/�� ���P �����藧�Ƃ͈�ʂɌ����Ȃ��̂ŁA�K���Ȓ�
�� ���@���߂邱�Ƃɂ��A
�@�r���f(�P)/�� �{ �� �� �P
�ƂȂ�悤�ɂł���B�@�����P�@�̂Ƃ��A�㎮�����藧�Ƃ������Ƃ́A�����O�@�̂Ƃ��A�O�ɂ�
��Ȃ�������Ȃ��̂ŁA�萔 �� �́A�r���f(��)/�� �̒萔����ł������悤�ɂ����悢�B
�@���̂Ƃ��A�@�r���|�P(��) ���r���f(��)/�� �{ ���@�ł���B
������A�@���E�r���|�P(��) ���r���f(��) �{ �����@�E�E�E�@�i�P�j�̎菇
�@���E��r���|�P(��)�������r��(��) �{ �������@�E�E�E�@�i�Q�j�̎菇
����āA�@�r��(��)�����E��r���|�P(��)���� �{ �������@�ɂ����āA
�@�@�r��(�P)���P�@�ƂȂ�悤�ɁA �� �̒l���߂�B�@�E�E�E�@�i�R�j�̎菇
�ȏ�̎菇����A�m���ɁA�r��(��) �����߂���킯�ł���B
��@�r4(��) �� (�P/�T)��5�{(�P/�Q)��4�{(�P/�R)��3�|(�P/�R�O)���@����A�r5(��)�@�����߂Ă݂�̂�
�@�y�����I
�@�T�r4(��)����5�{(�T/�Q)��4�{(�T/�R)��3�|(�P/�U)���@��ϕ����āA
�@(�P/�U)��6�{(�P/�Q)��5�{(�T/�P�Q)��4�|(�P/�P�Q)��2
�@�P�|�i(�P/�U)�{(�P/�Q)�{(�T/�P�Q)�|(�P/�P�Q)�j���O�@���A
�@�r5(��)��(�P/�U)��6�{(�P/�Q)��5�{(�T/�P�Q)��4�|(�P/�P�Q)��2
�i�R�����g�j�@�r ���炢���������������Q�l�ɘb��W�J�������A��L�̂悤�ȗ����ł���
�@�@�@�@�@�@�̂��ǂ��������s���ł���B���� �r ����̌������肢�������Ǝv���B
�@���̂悤�ɁA�P�ɁA�P�{�Q�{�R�{�E�E�E�{������(���{�P)/�Q�@�Ƃ����F�������Ȃ��ƁA�܂�Ȃ�
�������A�P�{�Q�{�R�{�E�E�E�{����(�P/�Q)��2�{(�P/�Q)���@�Ƃ������������邱�ƂɋC�����ƁA��R
����������P���Č�����B�����������ꂽ���͔̂��������A�������ꂾ���ł���B
�i�NjL�j�@�����P�X�N�P�P���Q�Q���t��
�@��L�̌v�Z������Ɏ��s���āA
�@�r6(��)��(�P/�V)��7�{(�P/�Q)��6�{(�P/�Q)��5�|(�P/�U)��3�{(�P/�S�Q)��
�@�r7(��)��(�P/�W)��8�{(�P/�Q)��7�{(�V/�P�Q)��6�|(�V/�Q�S)��4�{(�P/�P�Q)��2
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@���̂Ƃ��A�@�r5(��)�{�r7(��)���Q�o�r1(��)�p4
�Ƃ����������W�������藧�B�i�Ђ�����v�Z����Ɗm���߂���I�j
�@���̊W���́A���R�r�i1804�`1851�j�ɂ�蔭�����ꂽ���̂��Ƃ����B
�i�NjL�j�@�����Q�P�N�U���S���t��
�@��L�̊W���ɂ��āA�g�m�u�|���e�v������A�K���𗘗p�����ؖ��@����������������
���B�|���e����Ɋ��ӂ��܂��B
�@�i���{�P�j4�|�i���|�P�j4���W��3�{�W���@�ł��邱�Ƃ𗘗p���āA
�@��4�E�o�i���{�P�j4�|�i���|�P�j4�p����4�E�i�W��3�{�W���j���W�i��5�{��7�j
���Ȃ킿�A�@�o���i���{�P�j�p4�|�o���i���|�P�j�p4���W�i��5�{��7�j�@�����藧�B
�@�����ŁA�@�������o���i���{�P�j�p4�@�Ƃ����ƁA�㎮���A��5�{��7���i�����|����-1�j/�W
����āA�@�r5(��)�{�r7(��)���i�����|��0�j/�W���o���i���{�P�j�p4/�W���Q�o�r1(��)�p4
�i�R�����g�j�@�Ђ�����v�Z����Ǝv���Ă�����A��L�̂悤�ȊȖ��ȉ�@������̂ł��ˁB��
�@�@�@�@�@�@�����܂����B�|���e����ɂ��A�K���𗘗p���ă��v�Z���Y��ɉ��������
�@�@�@�@�@�@�ƂĂ��u�����Ƃ̂��ƁB���������ł��I
�@�|���e����̎�@��p����ƁA�P ���� �� �܂ł̎��R���̗����̘a�̌���
�@�@�@�P3�{�Q3�{�R3�{�E�E�E�{��3 ����2�i���{�P�j2/�S
�̏ؖ����ȒP�ɂł��邱�Ƃ��A�g�m�u�e�m�v�����育���������������B
�i�����Q�Q�N�S���P�T���t���D�D�D���܂荞�݂̏o���Œ������X�o���܂���ł�����(^^;)�B�j
�@�e�m����ɂ��A���̌����̏ؖ��̒��ŁA�ł��ȒP�ȏؖ��̈���Ƃ����B���̊Ȗ���
�Ɏ����������܂����B�e�m����Ɋ��ӂ��܂��B
�i�ؖ��j�@�i���{�P�j2�|�i���|�P�j2���S���@�ł��邱�Ƃ𗘗p���āA
�@��2�E�o�i���{�P�j2�|�i���|�P�j2�p���S��3�@�����A�o���i���{�P�j�p2�|�o���i���|�P�j�p2���S��3
�����藧�B�@�� �ɂP�C�Q�C�E�E�E�C���@�������A �� �̎���ӁX�����Ď������B�i�؏I�j
�@����ɁA���g�o�����������b�ɂȂ��Ă���r�i�g�j����ޑ���N�����������B�r�i�g�j��
��Ɋ��ӂ��܂��B
�@�r5(��)�{�P�O�r7(��)�{�T�r9(��)���P�U�o�r1(��)�p5
�@������A�|���e�����育���������������K���̎�@��p����Ηe�Ղ��낤�B
�@�i���{�P�j5�|�i���|�P�j5���Q�i�P�{�P�O��2�{�T��4�j�@�ł��邱�Ƃ𗘗p���āA
�@��5�E�o�i���{�P�j5�|�i���|�P�j5�p���Q��5�E�i�P�{�P�O��2�{�T��4�j���Q�i��5�{�P�O��7�{�T��9�j
�����A�@�o���i���{�P�j�p5�|�o���i���|�P�j�p5���Q�i��5�{�P�O��7�{�T��9�j�@�����藧�B
�@�����ŁA�@�������o���i���{�P�j�p5�@�Ƃ����ƁA�㎮���A��5�{�P�O��7�{�T��9���i�����|����-1�j/�Q
����āA�r5(��)�{�P�O�r7(��)�{�T�r9(��)���i�����|��0�j/�Q���o���i���{�P�j�p5/�Q���P�U�o�r1(��)�p5
�����藧�B
�@��L�̂Q�Ⴉ��@����ɁA���ӂ��^�����āA������v�Z�������ʁA�E�ӂƂȂ�̂ł͂Ȃ��A
�t�ɁA�E�ӂ��獶�ӂ����R�ɓ������悤���B
�i�NjL�j�@�K������̈�ʍ��̌v�Z�ŁA���̐���̘a�̌���
�@�@�P2�{�Q2�{�R2�{�E�E�E�{��2 �����i���{�P�j�i�Q���{�P�j/�U
�����A�ނ���A���̘a�̌����F�P2�{�Q2�{�R2�{�E�E�E�{�i���|�P�j2 �����i���|�P�j�i�Q���|�P�j/�U
�̕������p�����B���̂Ƃ��A�@���i���{�P�j�i�Q���{�P�j�|���i���|�P�j�i�Q���|�P�j���U��2
�Ƃ��������̑��݂ɋC�Â������B���̂��Ƃ���A���̐ϕ��̓���
�@�@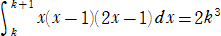
�̐��藧���Ƃ�������B�i���ӂ��A�� �Ɋւ��Ĕ������Ă݂�Ƃ悢�B�j
�@���������āA�u�P ���� �� �܂ł̎��R���̗����̘a�v�ɂ��āA�ϕ���p�����V�����ؖ�
�@�邱�Ƃ��ł���B���Ȃ킿�A�@
�@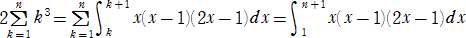
�ɂ����āA
�@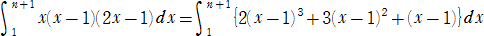
���A
�@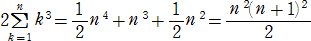
���������āA�@�P3�{�Q3�{�R3�{�E�E�E�{��3 ����2�i���{�P�j2/�S�@�����藧�B
�i�NjL�j�@�����Q�P�N�U���Q���t��
�@�u���R���̘a�v��u�������̘a�v�����߂�ꍇ�ɒ�ϕ���p�����@�͐V�N�ł���B
�@���Ƃ��A�u���R���̘a�v�����߂�ꍇ�́A�@�e1(��)�����{�P/�Q�@�ɂ��āA
�@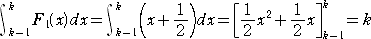
�ƂȂ邱�Ƃ���A
�@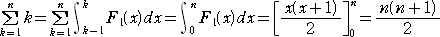
�@�Ƃ���ŁA�e1(��)�����{�P/�Q�@�͎��̂悤�ɂ��ċ��߂���B
�@�P�����@�e1(��)�������{���@�ɂ��āA
�@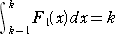
�����藧���̂Ƃ��āA���ӂ� �� �Ŕ�������ƁA�@�����{���|�o���i���|�P�j�{���p���P
�@������A�@�����P�@�ł���B���̂Ƃ��A��ϕ��̌v�Z����A
�@���|�P/�Q�{�������@���A�@�����P/�Q
����āA�����������P�����@�e1(��)�@�́A�@�e1(��)�����{�P/�Q�@�Ɗm�肷��B
�@���l�ɂ��āA�Q�����@�e2(��)������2�{�����{���@�ɂ��āA
�@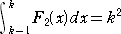
�����藧���̂Ƃ��āA���ӂ� �� �Ŕ�������ƁA
�@����2�{�����{���|�o ���i���|�P�j2�{���i���|�P�j�{���p���Q��
����āA�@�@�Q�����|���{�����Q���@���A�@���������P
�@���̂Ƃ��A��ϕ��̌v�Z����A�@��2�{���|�P/�U����2�@���A�@�����P/�U
����āA�����������Q�����@�e2(��)�@�́A�@�e2(��)����2�{���{�P/�U�@�Ɗm�肷��B
�@���́@�e2(��)����2�{���{�P/�U�@��p���āA
�@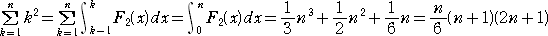
�ƁA�����̘a�����߂���B
�i�NjL�j�@���g�o�ǎ҂̂r�D�x����A��L�̘b��ɂ��ă��[���ɂĂ����e�����������B
�@�@�@�@�i�����Q�X�N�P�O���Q�R���t���j
�@����Ƃ���x�̊� X[n](x) ���ȉ��̂悤�ɒ�`���܂��B
�@X[n](x)=x^n - (x-1)^n (n�͎��R��)
�@������`���I�ɁAX^n = x^n -(x-1)^n �ƕ\���A�`���I��X��n�����ƌĂԂ��Ƃɂ��܂��B
(���ۂ� x ��n-1�����ł�)
�@�ȉ��A��́Ax=0 ����x �܂ł̐ϕ��A���́Ax=1 ���� n �܂ł̘a�Ƃ��܂��B
�@���̂Ƃ��A���̎������藧���܂��B
�i�P�j�@X=x-(x-1)=1
�i�Q�j�@�� X^n dx = 1/(n+1){X^(n+1)+(-1)^(n+1)}
�i�R�j�@�� X^m = n^m
�@�i�Q�j�̕⑫ (x��X�ɒ��ӂ��Ă�������)
�� X^n dx
=1/(n+1)[x^(n+1)-(x-1)^(n+1)] [0,x]
=1/(n+1){x^(n+1)-(x-1)^(n+1)-0+(-1)^(n+1)}
=1/(n+1){X^(n+1)+(-1)^(n+1)}
�@�i�R�j�̕⑫
�� X^m =��[1,n]{x^m -(x-1)^(m-1)}= n^m
�@x^m ��X�̌`���I��m+1�����ŕ\�����Ƃ��ł���A�i�R�j���a�̎������܂�܂��B
�Ⴆ�Ax=1/2 X^2 + 1/2 X�@�� ��x =1/2 n^2 + 1/2 n �Ȃǂł��B
�@���ɁA�a�̎������߂Ă����܂��B
x =�� 1 dx =�� X dx [�i�P�j���]=1/2 (X^2 +1) [�i�Q�j���]=1/2 X^2 + 1/2
�@=1/2 X^2 + 1/2X [�i�P�j���] �c�i�S�j
�@�� ��x = 1/2 n^2 +1/2 n [�i�R�j���]
����ɁA
x^2=�� 2x dx =�� (X^2+X) dx [�i�S�j���]=1/3 (X^3-1)+1/2 (X^2 +1) [�i�Q�j���]
�@ =1/3 X^3 +1/2 X^2 + 1/6=1/3 X^3 +1/2 X^2 + 1/6X [�i�P�j���] �c�i�T�j
�@�� ��x^2=1/3 n^3+ 1/2 n^2 +1/6 n [�i�R�j���]
�����āA
x ^3= �� 3x^2 dx =�� (X^3 +3/2X^2 +1/2X) dx [�i�T�j���]
�@�@=1/4 (X^4+1)+1/2 (X^3-1)+1/4 (X^2+1) [�i�Q�j���]=1/4X^4 +1/2 X^3 +1/4 X^2
�c�i�U�j
�@�� ��x^3=1/4n^4 +1/2 n^3 +1/4 n^2 [�i�R�j���]
�@�S��̘a�����߂�ƁA(������)
x ^4= �� 4x^3 dx =�� (X^4 +2X^3 +X^2) dx =1/5 (X^5-1)+1/2 (X^4+1)+1/3 (X^3-1)
�@�@=1/5X^5 +1/2 X^4 +1/3 X^3-1/30=1/5X^5 +1/2 X^4 +1/3 X^3-1/30X
�@�� ��x^4=1/5n^5 +1/2 n^4 +1/3 n^3-1/30n
�@��ʂɁAm��0 �̐����ɂ��āAx^m = S[m](X) (X�̌`���I��m+1 ����) �Ƃ����ƁA
(�C)�@��x^m=S[m](n) �����藧�B
(��)�@x^m = �� mx^(m-1) dx ���AS[m](X)= m �� S[m-1](X) dx �����B
(�n)�@S[0](X)=1=X ����Ax^m =S[m](X)=m ! ���c X (dx)^m �ƕ\�����Ƃ��ł���B
�@�����̐ϕ��́i�P�j�A�i�Q�j�A�i�R�j��p���čs���B
�@�i�P�j�� X=1 �� �|�C���g�������Ǝv���܂����B
�i�⑫�P�j�@x^m =m ! ���c (dx)^m �Ƃ��\����B
�i�⑫�Q�j�@x^m =S[m](X) �̍��ӂ�x = 1 ���������1 �ɂȂ�B
�@�@�@�@�@�܂��A�E�ӂ̊e�� �� X^k=X[k](x)=x^k -(x-1)^k��x=1��������� X[k](1)=1
�@�@�@�@�@X=1 ��� S[m](X)= a[m+1] X^(m+1)+�c +CX �̌`�ɂȂ�AC�� mS[m-1](X) ���`��
�@�@�@�@�@�I�ȕs��ϕ�������(�Ō�̍��� �cCX) �Ax =1 (���Ȃ킿X^k=1)�������Č��肵��
�@�@�@�@�@���悢�B(S����̉�@�̍����ɂȂ�܂��B)
�i�R�����g�j�@��@�����ł��ˁI�r�D�x����Ɋ��ӂ��܂��B
�i�NjL�j�@�����P�X�N�R���V���t��
�@��L�ŁA�@�@���i���{�P�j�i�Q���{�P�j�|���i���|�P�j�i�Q���|�P�j���U��2�@�@�Ƃ��������̑��݂�
�r���𗁂т����A���̓�����w�i�Ƃ����肪�����P�X�N�x�}�g��w�O�������ŏo�肳��
���B�}�g��w�͖��N���̍������������o�肷��Ƃ����_�ł������ڂ��Ă���I
�}�g��w�O���i�Q�O�O�V�j
�i�P�j�@��ʍ� ��n ���A�@����3�{����2�{�����@�ŕ\����鐔�� �o ��n �p�ɂ����āA
�@�@��2����n�{1�|��n�@�@�i�����P�A�Q�A�R�A�E�E�E�j
�����藧�悤�ɁA�萔 �� �A �� �A �� ���߂�B
�i�Q�j�@�i�P�j�̌��ʂ�p���āA
�@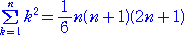
�ƂȂ邱�Ƃ������B�@�i�i�R�j�͗��j
�@��L�̓����ɂ��A�i�P�j�́A�@�����P/�R�@�A�@�����|�P/�Q�@�A�@�����P/�U�@�Ƒ������낤�I
�i�������A�������̓��ĂƂ��ẮA�P�����̐�����p���Ă�������_�q���Ȃ��Ɠ_���ɂ�
�Ȃ�Ȃ���������Ȃ��B�j
�@�i�Q�j���A���̔w�i�ɁA�@�����P�@�ɑ���
�@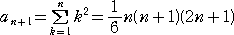
�Ƃ������Ƃ��������Ă���A
�@�i��2�|��1�j�{�i��3�|��2�j�{�E�E�E�i��n�{1�|��n�j����n�{1�|��1����n�{1
����A���炩�ɓ��������藧���A��͂�A�������O�b�Ɗ����āA�ׁX�Ƃ����v�Z��
�ĂɎ����Ă����Ȃ��ƍ��i�_�͂��Ȃ����낤�B
�i�NjL�j�@�����Q�Q�N�R���P�S���t��
�@���g�o�����������b�ɂȂ��Ă���g�m�u�f�`�h�v���A�u�����Ђ�����̕��@�v�Ƒ肵��
�u�P ���� �P�O �܂ł̎��R���̂P�O��̘a�v�ɂ��āA�Ђ����玆�Ɖ��M�������g�p���A
��ԉɂ����ċ��߂Ă������@�ɂ��āA�����Q�Q�N�R���P�O���t���œ��g�o�̌f���u�o
��̐�v�ɏ������܂ꂽ���̂��Љ�����Ǝv���B
�v�Z��@�̃R�c
�@���̂Q�̌������ǂ����o���Ă����B
�������P���@�Pk�{�Qk�{�Rk�{����{��k���o�i���{�P�{�a�jk+1�|�ak+1�p/�i���{�P�j
�������Q���@�a�� �́@�i�a�{�P�jk���ak�@�̓W�J���@�i�����P�j����Q�����肵�Ă����B
�@���ۂ̌v�Z�͎��̂悤�ɍs���B
�i�P�j�@�܂��A�����Q �ɂ����āA�����Q �Ƃ��A�i�a�{�P�j2���a2�@��W�J���āA�a1���|�P/�Q
�@���l�ɁA�@�i�a�{�P�j3���a3�@��W�J���āA�a2���P/�U
�@�i�a�{�P�j4���a4�@��W�J���āA�a3���O
�@�i�a�{�P�j5���a5�@��W�J���āA�a4���|�P/�R�O
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�����n���ɑ����Ă����ƁA�x���k�[�C�����o������B
�a5���O�@�A�a6���P/�S�Q�@�A�a7���O�@�A�a8���|�P/�R�O�@�A�a9���O�@�A�a10���T/�U�U�@�A�E�E�E
�@�����ŁA�����ɁA�����P��p���āA���R���̕����̘a�����߂Ă݂悤�B
�@�P2�{�Q2�{�R2�{�E�E�E�{��2
���o�i���{�P�{�a�j3�|�a3�p/�R
���o�i���{�P�j3�{�R�i���{�P�j2�a�{�R�i���{�P�j�a2�p/�R
���i���{�P�j�o�Q�i���{�P�j2�|�R�i���{�P�j�{�P�p/�U�����i���{�P�j�i�Q���{�P�j/�U
�@���l�̌v�Z���A
�@�@�P10�{�Q10�{�R10�{�E�E�E�{�P�O10���o�i�P�P�{�a�j11�|�a11�p/�P�P
�ɂ��čs���悢�B
�@�o�i�P�P�{�a�j11�|�a11�p/�P�P
���P�P10�{�P�P10�a�{�T�E�P�P9�a2�{�P�T�E�P�P8�a3�{�R�O�E�P�P7�a4�{�S�Q�E�P�P6�a5
�@�{�S�Q�E�P�P5�a6�{�R�O�E�P�P4�a7�{�P�T�E�P�P3�a8�{�T�E�P�P2�a9�{�P�P�a10
���P�P10�|�P�P10/�Q�{�T�E�P�P9/�U�|�P�P7�{�P�P5�|�P�P3/�Q�{�T/�U
���P�P10/�Q�{�T�E�P�P9/�U�|�P�P7�{�P�P5�|�P�P3/�Q�{�T/�U
�@�����ŁA�@�P�P10���Q�T�X�R�V�S�Q�S�U�O�P�@�A�P�P9���Q�R�T�V�X�S�V�U�X�P�@�A�P�P7���P�X�S�W�V�P�V�P
�P�P5���P�U�P�O�T�P�@�A�P�P3���P�R�R�P�@�Ȃ̂ŁA������Čv�Z����ƁA
�P�S�C�X�P�S�C�R�S�P�C�X�Q�T�@�ƂȂ�B
�i�R�����g�j�@��L�̌v�Z�̌��ɁA�d�������� ����̂����b�ɂȂ�܂����D�D�D��(^^;)
�@�܂��A��L�̌v�Z�Ɏ��̃z�[���y�[�W���Q�l�ɂ����Ă��������܂����B
�@���w�I�v�l�ƉȊw�I�v�l�@(�P�X�X�W�N�Q�w���@�ؗj�P��)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�x���k�[�C���̂͂Ȃ��@�|�����ׂ̂���̘a�ƌ�㏇��|
�i���ɋ����w�̑�w�@�������̍u�`�^�j�@���ɋ����w���R�n���w�@���R�@�A�@����
�@�܂��A�f�`�h ����̉�@�Ƃ͈���āA�r����̎�@�����p���āA����
�@�r1(��) �� (�P/�Q)��2�{(�P/�Q)��
�@�r2(��) �� (�P/�R)��3�{(�P/�Q)��2�{(�P/�U)��
�@�r3(��) �� (�P/�S)��4�{(�P/�Q)��3�{(�P/�S)��2
�@�r4(��) �� (�P/�T)��5�{(�P/�Q)��4�{(�P/�R)��3�|(�P/�R�O)��
�@�r5(��)��(�P/�U)��6�{(�P/�Q)��5�{(�T/�P�Q)��4�|(�P/�P�Q)��2
�@�r6(��)��(�P/�V)��7�{(�P/�Q)��6�{(�P/�Q)��5�|(�P/�U)��3�{(�P/�S�Q)��
�@�r7(��)��(�P/�W)��8�{(�P/�Q)��7�{(�V/�P�Q)��6�|(�V/�Q�S)��4�{(�P/�P�Q)��2
�@�r8(��)��(�P/�X)��9�{(�P/�Q)��8�{(�Q/�R)��7�|(�V/�P�T)��5�{(�Q/�X)��3�|(�P/�R�O)��
�@�r9(��)��(�P/�P�O)��10�{(�P/�Q)��9�{(�R/�S)��8�|(�V/�P�O)��6�{(�P/�Q)��4�|(�R/�Q�O)��2
�@�r10(��)��(�P/�P�P)��11�{(�P/�Q)��10�{(�T/�U)��9�|��7�{��5�|(�P/�Q)��3�{(�T/�U�U)��
�ƁA�قڋ@�B�I�ɋ��߂���̂ŁA������𗘗p���Ă��������낤�B
�@���̂Ƃ��A�@�r10(�P�O)���P�S�C�X�P�S�C�R�S�P�C�X�Q�T�@�ł��邱�Ƃ�������B
�@���R���ׂ̂���a�̎��ɂ��āA�f�`�h �������N�ł��B�i�����Q�S�N�P���Q�X���t���j
�@S(��)���Pk�{�Qk�{�Rk�{�E�E�E�{��k�@��\�����́A���ꂼ������Ƃ��ċL�q����Ă��邪�A����
��ɂ́A���̐��������藧���Ƃ�m��܂����B
�@���F��̏ꍇ�@���@S(��)�́AS(�P)�̑������ŕ\�����B
�@���F�����̏ꍇ�@���@S(��)�́AS(�Q)�Ŋ���A���̏��́A�܂��AS(1)�̑������ŕ\�����B
�@������A��̓I�Ɏ��ɂ��Ă݂܂����B�������A�\�L���֗��Ȃ悤�ɁAA��S(�P)�AB��S(�Q)�ŕ\
���܂��B
�@S(�R)��A2
�@S(�S)��(�UA�|�P)B/�T
�@S(�T)��(�SA�|�P)A2/�R
�@S(�U)��(�P�QA2�|�UA�{�P)B/�V
�@S(�V)��(�UA2�|�SA�{�P)A2/�R
�@S(�W)��(�S�OA3�|�S�OA2�{�P�WA�|�R)B/�P�T
�@S(�X)��(�QA�|�P)(�WA2�|�UA�{�R)A2/�T
S(�P�O)��(�QA�|�P)(�Q�SA3�|�Q�WA2�{�Q�OA�|�T)B/�P�P
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@��������ʓI�ɕ\���鎮�Ƃ��č��Ȃ����̂ł��傤���H�����m�̕��͂��m�点�������B
�@�您��������̃R�����g�ł��B�i�����Q�S�N�P���Q�X���t���j
�@��L�ɁA������x�̂��Ƃ͏�����Ă���Ǝv���܂��B�܂��́A�u���C�ɓ���W�v����A�炷
���邳��̃T�C�g�u����a�̌����v�ɍs�����c�B
�@��M����̃R�����g�ł��B�i�����Q�S�N�P���R�O���t���j
�@���F��̏ꍇ�@���@S(��)�́AS(�P)�̑������ŕ\�����B
�@���F�����̏ꍇ�@���@S(��)�́AS(�Q)�Ŋ���A���̏��́A�܂��AS(1)�̑������ŕ\�����B
�Ƃ��������́AS(��)��f(��) ���A�@f(���{�P)�|f(��)���i���{�P�jk�@�Af(�O)���O�@�������Ɠ����l��
��Əؖ��ł��܂����B����قǓ���Ȃ��Ǝv���܂��̂ł��Ѝl�@���D�D�D�B
�@��������ʓI�ɕ\���鎮�Ƃ����͓̂�����ł����A�������Ă݂�ƁA�x���k�[�C���Ƃ�
�������g���āA��ʓI�ɁA�i���̑������Ƃ��Ăł����j�\�����@�����邻���ł��B
�@�r�i�g�j����̃R�����g�ł��B�i�����Q�S�N�P���R�O���t���j
�@���́uDonald E. Knuth�v�搶���A�֘A���āG
�@�uJohann Faulhaber and Sums of Powers�v�A�uJohann Faulhaber�v�A�u����̘a�v
�i�ǐL�j�@���v�Z���������ɂ�ŁA�ʂɁA�Ⴆ�A169+269+�E�E�E+n69 �����r�i�V�O�j
�@�܂��A�r�i�P�T�j�@�A�r�i�P�V�j�@�A�E�E�E�A�r�i�P�U�X�j�@���������ɂ�ŁB
�@���g�o�̓ǎ҂̂j�r������A�����Q�S�N�V���Q�W���t���ŗݏ�a�̌����ɂ��āA���[����
�������B
�i�P�j�@�x���k�[�C�̌����𗘗p
�@�@�P���{�Q���{�R���{�E�E�E�{�i���|�P�j��
���o�i����+1�{��+1�b1�a1�����{�E�E�E�{��+1�b���a�����p/�i���{�P�j
���o�i���{�a�jk+1�|�ak+1�p/�i���{�P�j�@�i���@�`���I�\�L�j
�@�������A�@�a0���P�@�A����=0�`�� ��+1�b���a�����O�@�i�����P�A�Q�A�R�A�E�E�E�j
�@��L�Ōv�Z�����悤�ɁA�����@�i�a�{�P�j�����a���@��W�J���邱�Ƃɂ��A�x���k�[�C������
����B
�a0���P�@�A�a1���|�P/�Q�@�A�a2���P/�U�@�A�a3���O�@�A�a4���|�P/�R�O�@�A�a5���O�@�A�a6���P/�S�Q
�a7���O�@�A�a8���|�P/�R�O�@�A�a9���O�@�A�a10���T/�U�U�@�A�E�E�E
�@�x���k�[�C����p���āA
�@������/�i�����|�P�j������=0�`�� �a������/���I
�@����=0�`�� ����������=0�`�� ���b���a���E�i���{�P�j��+1-��/�i���{�P�|���j
��@�����R�@�̂Ƃ��A
����=0�`�� ��3
������=0�`3 3�b���a���E�i���{�P�j4-��/�i�S�|���j
���a0�E�i���{�P�j4/�S�{3�b1�a1�E�i���{�P�j3/�R�{3�b2�a2�E�i���{�P�j2/�Q�{3�b3�a3�E�i���{�P�j
���i���{�P�j4/�S�|�i���{�P�j3/�Q�{�i���{�P�j2/�S
�i�Q�j�@�����̗��p
�@�rk�f(��)�����E�r��-1(��)�{�rk�f(�O)�@�@�������A�@�rk�f(�O)���a��
�@���ʂ̎�������ϕ����A�ϕ��萔���@�rk(�P)���P�@�ɂ��m�肷��B�܂��A�x���k�[�C��
�a�����O�@�i���͂R�ȏ�̊�j�@�𗘗p����B
�i�R�����g�j�@�ގ��̌v�Z����L�ɂ���̂ŎQ�l�ɂ��Ă��������B�@
�i�R�j�@�K���
�@�W�����A���X�^�[�����O������A���X�^�[�����O���ɂ���鏸�K��̂Ƃ��́A������
���݂ɂȂ�B
�@[�w]�����w�i�w�{�P�j�E�E�E�i�w�{���|�P�j�@�A�@[�w]�����w�i�w�|�P�j�E�E�E�i�w�|���{�P�j
�@����=1�`��[�w]����[��]��+1/�i���{�P�j�@�A�@����=1�`��[�w]����[��]��+1/�i���{�P�j
�@[�w]n������=0�`�� ���b���w���@�A�@[�w]n������=0�`�� (�|�P�j��-�����b���w��
�@�wn������=0�`�� (�|�P�j��-�����b��[�w]���@�A�@�wn������=0�`�� ���b��[�w]��
�@����=1�`���w��������=0�`�� (�|�P�j��-�����b��[��]��/�i���{�P�j
�@����=1�`���w��������=0�`�� ���b��[���{�P]��/�i���{�P�j
�i�S�j�@�A���������̗��p�i�W�J���j
�@����=1�`�� ���������E����+1�{���E�����{�E�E�E�{���@�Ƃ����āA�����P�A�Q�A�E�E�E�A���{�P�������A���A
���A�E�E�E�A���̘A���������������B
�i�T�j�@���ȏ��ɂ�����@
�i���{�P�j���|���������E����-1�{�E�E�E�{�P
�����|�i���|�P�j�������E�i���|�P�j��-1�{�E�E�E�{�P
�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�Q���|�P�������E�P�{�E�E�E�{�P
�ӁX�����āA�@�i���{�P�j���|�P��������=1�`�� ����-1�{�E�E�E�{��
�@��́A���|�P��ȉ��̘a�̌����𗘗p����B
�i�U�j�@�t�@�E���n�[�o�[�̒藝
�@�ԁ����i���{�P�j/�Q�@�Ƃ����ƁA
������1 ��2r+1���i������+1�{�E�E�E�{����2�̌`�j
������1 ��2r���i�Q���{�P�j�i�������{�E�E�E�{���Ԃ̌`�j
�i�V�j�@���K�����@�𗘗p�i�g�����̐��ŕ\������j
�@����=1�`�� ��3�����b1�{�V�E���b2�{�P�Q�E���b3�{�U�E���b4
�������A�W���́A
�@���c������-1�c��-1�{���E��-1�c���@�A���c0���P�@�A���c�������I�@�A���c�����O�@�i�������j
�i�W�j�@�g�����̐��i�b�j�őΏ̓I�ɕ\������B
�@�I�C���[�̌W���ŗ^������B
��2�����b1�{�Q�E���b2����+1�b2�{���b2�@���A�@����=1�`�� ��2����+2�b3�{��+1�b3
��3�����b1�{�U�E���b2�{�U�E���b3�����b3�{�S�E��+1�b3�{�U�E��+2�b3�@���A
�@����=1�`�� ��3����+1�b4�{�S�E��+2�b4�{��+3�b4
�����ŁA�@���c�����i���{�P�|���j��-1�c��-1�{���E��-1�c���@�A���c1�����c�����P�@�i�I�C���[�̐��j
���̂Ƃ��A�@����=1�`�� ���������c1�E��+1�b��+1�{���c2�E��+2�b��+1�{�E�E�E�{���c���E��+���b��+1
�i�X�j�@��ԖڂƓ�Ԗڎ����͂����ɂ킩��̂ŁA���̌W���͈ȉ��̔�r�ŋ��߂邱�Ƃ���
�@�@�@����
��@����=1�`�� ��4����5/�T�{��4/�Q�{����3�{����2�{����
�@�@���i���{�P�j5/�T�|�i���{�P�j4/�Q�{���i���{�P�j3�{���i���{�P�j2�{���i���{�P�j
�������āA�����P/�R�@�A�����O�@�A�����|�P/�R�O
�@�ȏォ��A
�@����=1�`�� ��3���i���{�P�j4/�S�|�i���{�P�j3/�Q�{�i���{�P�j2/�S�@�@�@�i�x���k�[�C�j
�@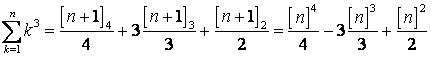 �@�@�i�X�^�[�����O�j
�@�@�i�X�^�[�����O�j
�@����=1�`�� ��3�����b1�{�V�E���b2�{�P�Q�E���b3�{�U�E���b4�@�@�@�i�X�^�[�����O�j
�@����=1�`�� ��3����+1�b4�{�S�E��+2�b4�{��+3�b4�@�@�@�i�I�C���[�̑Ώ̐��j
�@����=1�`�� ��3����4/�S�{��3/�Q�{��2/�S�@�@�@�i����W���j
�@����=1�`�� ��3����2�@�@�@�i�t�@�E���n�[�o�[�j
�i�R�����g�j�@�j�D�r�D����A�������e���肪�Ƃ��������܂��B�u�t�@�E���n�[�o�[�v�Ƃ������O��
�@�@�@�@�@�@�����ł����I
�i�⑫�j�@�ߘa�T�N�V���Q�S���t��
�@��L�ł́A�����̌`�Ő���̘a�����߂邱�Ƃ���X�s�����B���̂��Ƃ���ʉ����āA����
�悤�ȃ}�j���A�������邱�Ƃ��ŋߒm�邱�Ƃ��ł����B
�@�A�������m�̐����̐ς��A�f�m�i���j�����i���{�P�j�i���{�Q�j�E�E�E�i���{�m�|�P�j�ŕ\���Ƃ���B
�@���̂Ƃ��A�@�f1�i���j�����A�f2�i���j�����i���{�P�j�A�E�E�E�@�ł���B
�@�u�����l�������v�Ŏ��������� �F �e���{�P(�w�{�P)�|�e���{�P(�w)���i���{�P)�e��(�w�{�P)�@����
�@�f�m+1�i���j�|�f�m+1�i���|�P�j���i�m�{�P)�f�m(��)
�����藧�B
��@�m���P�@�̂Ƃ��A�@���i���{�P�j�|�i���|�P�j�����Q��
�m���Q�@�̂Ƃ��A�@���i���{�P�j�i���{�Q�j�|�i���|�P�j���i���{�P�j���R���i���{�P�j
�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@���̗Ⴉ���������悤�ɁA�����A����2�A�E�E�E�@�̌���������������B
�@�܂��A�f�m+1�i���j�|�f�m+1�i���|�P�j���i�m�{�P)�f�m(��)�@�ɂ����āA
�@�����P�A�Q�A�E�E�E�A���@������������A�ӁX�����邱�Ƃɂ��A
�f�m+1�i���j�|�f�m+1�i�O�j���i�m�{�P)�i�f�m(�P)�{�f�m(�Q)�{�E�E�E�{�f�m(��)�j
�@�������A�f�m+1�i�O�j���O�@�Ȃ̂ŁA
�@����=1�`�� �f�m(��)���f�m+1�i���j/�i�m�{�P)
�����藧�B�i���ƂȂ��A�s��ϕ��̌����Ɏ��Ă��܂��ˁI�j
�@���̌�����p����ƁA
����=1�`�� ��������=1�`�� �f1(��)���f2�i���j/�Q�����i���{�P�j/�Q
����=1�`�� ���i���{�P�j������=1�`�� �f2(��)���f3�i���j/�R�����i���{�P�j�i���{�Q�j/�R
����=1�`�� ���i���{�P�j�i���{�Q�j������=1�`�� �f3(��)���f4�i���j/�S�����i���{�P�j�i���{�Q�j�i���{�R�j/�S
����=1�`�� ���i���{�P�j�i���{�Q�j�i���{�R�j
�@������=1�`�� �f4(��)���f5�i���j/�T�����i���{�P�j�i���{�Q�j�i���{�R�j�i���{�S�j/�T
����=1�`�� ���i���{�P�j�i���{�Q�j�i���{�R�j�i���{�S�j
�@������=1�`�� �f5(��)���f6�i���j/�U�����i���{�P�j�i���{�Q�j�i���{�R�j�i���{�S�j�i���{�T�j/�U
�Ȃǂ�������B
����āA
����=1�`�� ��2������=1�`�� ���i���{�P�j�|����=1�`�� ��
�����i���{�P�j�i���{�Q�j/�R�|���i���{�P�j/�Q�����i���{�P�j�i�Q���{�S�|�R�j/�U�����i���{�P�j�i�Q���{�P�j/�U
����=1�`�� ��3������=1�`�� �i���|�P�j���i���{�P�j�{����=1�`�� ��
������=1�`��-1 ���i���{�P�j�i���{�Q�j�{����=1�`�� ��
���i���|�P�j���i���{�P�j�i���{�Q�j/�S�{���i���{�P�j/�Q����2�i���{�P�j2/�S
����=1�`�� ��4������=1�`�� �i��4�|��2�j�{����=1�`�� ��2
������=1�`�� �i���|�P�j���i���{�P�j�i���{�Q�j�|�Q����=1�`�� �i���|�P�j���i���{�P�j�{����=1�`�� ��2
������=1�`��-1 ���i���{�P�j�i���{�Q�j�i���{�R�j�|�Q����=1�`��-1 ���i���{�P�j�i���{�Q�j�{����=1�`�� ��2
���i���|�P�j���i���{�P�j�i���{�Q�j�i���{�R�j/�T�|�i���|�P�j���i���{�P�j�i���{�Q�j/�Q�{���i���{�P�j�i�Q���{�P�j/�U
���i���|�P�j���i���{�P�j�i���{�Q�j�i�Q���{�P�j/�P�O�{���i���{�P�j�i�Q���{�P�j/�U
�����i���{�P�j�i�Q���{�P�j�i�R��2�{�R���|�P�j/�R�O
����=1�`�� ��5������=1�`�� �i��5�|��3�j�{����=1�`�� ��3
������=1�`�� ���i���{�P�j�i���|�P�j�i��2�|�S�{�S�j�{����=1�`�� ��3
������=1�`�� �i���|�Q�j�i���|�P�j���i���{�P�j�i���{�Q�j�{�S����=1�`�� �i���|�P�j���i���{�P�j�{����=1�`�� ��3
������=1�`��-2 ���i���{�P�j�i���{�Q�j�i���{�R�j�i���{�S�j�{�S����=1�`��-1 ���i���{�P�j�i���{�Q�j�{����=1�`�� ��3
���i���|�Q�j�i���|�P�j���i���{�P�j�i���{�Q�j�i���{�R�j/�U�{�i���|�P�j���i���{�P�j�i���{�Q�j�{��2�i���{�P�j2/�S
����2�i���{�P�j2�i�Q��2�{�Q���|�P�j/�P�Q
�i�NjL�j�@�����Q�T�N�S���X���t��
�@�r��(��)���Pk�{�Qk�{�Rk�{����{��k�@�ɂ��āA���É���w�Ŏ��̂悤�Ȗ�肪�o�肳�ꂽ�B
������w�@���n�i�Q�O�P�R�j
�@���A���A���͐����Ƃ��A�����P�Ƃ���B���b����W���Ƃ��āA�r��(��)�A�s��(��)���ȉ��̂悤��
��߂�B
�@�r��(��)���Pk�{�Qk�{�Rk�{����{��k�@�A�r��(�P)���P�@�i�����O�j
�@�s��(��)�����b1�r1(��)�{���b2�r2(��)�{���b3�r3(��)�{�E�E�E�{���b��-1�r��-1(��)
�@������=1�`��-1 ���b���r��(��)�@�i�����Q�j
�i�P�j�@�s��(�P)�Ƃs��(�Q)�����߂�B
�i�Q�j�@��ʂ̂��ɑ��āA�s��(��)�����߂�B
�i�R�j�@�����R�ȏ�̑f���̂Ƃ��A�r��(���|�P)�@�i�����P�A�Q�A�R�A�E�E�E�A���|�Q�j �́A���̔{���ł���
�@�@���Ƃ������B
���a�̌������Ƃ��ɏo�Ă��鎮�Ɋւ�����ňꌩ����������A�撣���Ă݂鉿�l��
�@���肻���D�D�D�Ƃ������ƂŁA�ډ��ɒ��킵�Ă݂��B
�i���j�i�P�j�@�s��(�P)�����b1�r1(�P)�{���b2�r2(�P)�{���b3�r3(�P)�{�E�E�E�{���b��-1�r��-1(�P)
�@�����b1�{���b2�{���b3�{�E�E�E�{���b��-1
�@�����b0�{���b1�{���b2�{���b3�{�E�E�E�{���b��-1�{���b���|�i���b0�{���b���j
�@���Q���|�i�P�{�P�j���Q���|�Q
�@�s��(�Q)�����b1�r1(�Q)�{���b2�r2(�Q)�{���b3�r3(�Q)�{�E�E�E�{���b��-1�r��-1(�Q)
�@�����ŁA�@�r��(�Q)���Pk�{�Qk���P�{�Qk�@�Ȃ̂ŁA
�@�s��(�Q)���i���b1�{���b2�{���b3�{�E�E�E�{���b��-1�j
�@�@�@�@�@�@�{���b1�E�Q�{���b2�E�Q2�{���b3�E�Q3�{�E�E�E�{���b��-1�E�Q��-1
�@���i�Q���|�Q�j�{���b1�E�Q�{���b2�E�Q2�{���b3�E�Q3�{�E�E�E�{���b��-1�E�Q��-1
�@�w�����b1�E�Q�{���b2�E�Q2�{���b3�E�Q3�{�E�E�E�{���b��-1�E�Q��-1�@�Ƃ����ƁA
�@�w���i�P�{�Q�j���|���b0�|���b���E�Q�����R���|�P�|�Q��
�@����āA�@�s��(�Q)���i�Q���|�Q�j�{�R���|�P�|�Q�����R���|�R
�i�Q�j�@�i�P�j���A�s��(��)���i���{�P�j���|�i���{�P�j�@�Ɨސ������B���̗ސ������������Ƃ𐔊w
�@�@�I�A�[�@�ɂ�莦���B
�@�����P�@�̂Ƃ��A�i�P�j��薾�炩�ɐ��藧�B
�@�������i�����P�j�̂Ƃ����藧�Ɖ��肷��B���Ȃ킿�A�s��(��)���i���{�P�j���|�i���{�P�j
���̂Ƃ��A
�@�s��(���{�P)���� ��=1�`��-1 ���b���r��(���{�P)
���� ��=1�`��-1 ���b���o�r��(��)�{�i���{�P�j���p
���s��(��)�{�� ��=1�`��-1 ���b���i���{�P�j��
���s��(��)�{�o�P�{�i���{�P�j�p���|�P�|�i���{�P�j��
���i���{�P�j���|�i���{�P�j�{�i���{�Q�j���|�P�|�i���{�P�j�����i���{�Q�j���|�i���{�Q�j
�@����āA�������{�P�̂Ƃ������藧�B
�@�ȏォ��A���ׂĂ̎��R�����ɂ��āA�@�s��(��)���i���{�P�j���|�i���{�P�j�@�����藧�B
�i�R�j�@�r��(���|�P)�@�i�����P�A�Q�A�R�A�E�E�E�A���|�Q�j �́A���̔{���ł���ł��邱�Ƃ��A���ɂ�
�@�Ă̐��w�I�A�[�@�Ŏ����B
�@�����P�@�̂Ƃ��A�@�r1(���|�P)���P�{�Q�{�E�E�E�{�i���|�P�j�����i���|�P�j/�Q
�@�����ŁA���͂R�ȏ�̑f�����Ȃ킿��ł���̂ŁA�i���|�P�j/�Q�͐����B
�@����āA�r1(���|�P)�͂��̔{���ł���B
�@�����P�A�Q�A�R�A�E�E�E�A���@�i�������|�R�j�̂Ƃ��A�r��(���|�P)�͂��̔{���ł���Ɖ��肷��B
�@�s��(��)�����b1�r1(��)�{���b2�r2(��)�{���b3�r3(��)�{�E�E�E�{���b��-1�r��-1(��)
�@�@���� ��=1�`��-1 ���b���r��(��)�@�i�����Q�j
�ɂ����āA�������{�Q�A�������|�P�@�Ƃ����ƁA
�@�s��+2(���|�P)����+2�b1�r1(���|�P)�{��+2�b2�r2(���|�P)�{�E�E�E�{��+2�b��+1�r��+1(���|�P)
�@�����ŁA�i�Q�j���A�s��+2(���|�P)������+2�|���@�Ȃ̂ŁA
�@��+2�b��+1�r��+1(���|�P)������+2�|���|�i��+2�b1�r1(���|�P)�{�E�E�E�{��+2�b���r��(���|�P)�j
�@�A�[�@�̉���ɂ��A�E�ӂ́A���̔{���B���Ȃ킿�A�i���{�Q�j�r��+1(���|�P)�́A���̔{���B
�@�����ŁA���{�Q�����|�P�@�ŁA�� �͑f���Ȃ̂ŁA���{�Q �́A�� �Ŋ����Ȃ��B
�@����āA�r��+1(���|�P)�́A���̔{���łȂ���Ȃ�Ȃ��B
�@����́A�������{�P�̂Ƃ������肪���藧���Ƃ������B
�ȏォ��A�����R�ȏ�̑f���̂Ƃ��A
�@�r��(���|�P)�@�i�����P�A�Q�A�R�A�E�E�E�A���|�Q�j �́A���̔{���ł���
���Ƃ������ꂽ�B�@�@�i�I�j
�@���R���̙p��a�v�Z�ɂ��āA�f�`�h ����̑���ł��B�i�����Q�V�N�U���P�W���t���j
�@�@���R���̙p��a�����߂Ă�����A
�@��p�ł́A�����@n(n+1)�@�A�����p�ł́A�����@n(n+1)(2n+1)
�����ʂɊ܂ނ��Ƃ���A
�@��p�ł́As[1]=1+2+3+���+n�@�A�����p�ł́As[2]=12+22+32+���+n2
�����𗊂�ɋ��܂�Ȃ����̂��ƒ��킵�Ă݂܂����B�i�p�����傫���Ȃ�ƌ��������\���G�j
�@1+2+3+���+n=n(n+1)/2�̒l�����Ƃ�����A���R���̊�p�̘a
�@s[r]=1r+2r+3r+���+nr�@�ir�͊�j
�����̒l�����Ɏ��̌v�Z�ŋ��܂�B
s[3]=��2�@�As[5]=(1/3)��2(-1+4��)�@�As[7]=(1/3)��2(1-4��+6��2)�@�As[9]=(1/5)��2(-1+2��)(3-6��+8��2)
s[11]=(1/3)��2(5-20��+34��2-32��3+16��4)
s[13]=(1/105)��2(-691+2764��-4720��2+4592��3-2800��4+960��5)
s[15]=(1/3)��2(105-420��+718��2-704��3+448��4-192��5+48��6)
s[17]=(1/45)��2(-10851+43404��-74220��2+72912��3-46880��4+21120��5-6720��6+1280��7)
s[19]=(1/105)��2(219335-877340��+1500334��2-1474592��3
�@�@+950544��4-433536��5+145824��6-35840��7+5376��8)
�@�@���������
��������G�Ƃ����Ε��G���ȁ`�B����Ɋ֘A�����āA
�@12+22+32+���+n2=n(n+1)(2n+1)/6 �̒l��y�Ƃ����Ƃ��A���R���̋����p�̘a
�@s[s]=1s+2s+3s+���+ns�@�is�͋����j
��y�̒l�����Ɍv�Z�ł��܂��ˁH���낢�뎎�݂���ł����A�ڍ����܂����B
�@�r�i�g�j����̃R�����g�ł��B�i�����Q�V�N�U���P�W���t���j
�@�� = n (1 + n)/2�Ay = n (1 + n) (1 + 2 n)/6 �Ƃ��āAQ(x�Cy)�̌��Ƃ��āA�L�����ŕ\���\�ł��I
�@�Ⴆ�As[4]=(-7y + 972y3)/(5 (7 + 42�� + 144��2))
s[6]=(5y - 22���� + 108��3)/(7 (5 + 8��))
s[8]=(-21y + 86���� - 360��3 + 600����3)/(5 (21 + 40��))
s[10]=(2125y - 8550���� + 30420��3 - 41040����3 + 55728��5 -31104����5)/(11 (425 + 840�� - 576��2))
s[10]= (1/44)(20y - 120���� + 315��2y - 387��3 + 216����3)��Q[���C��] �Ƃ�������B
�@�f�`�h ����̃R�����g�ł��B�i�����Q�V�N�U���P�W���t���j
�@�����p���Ă����Ȃ�A
s[4]=(6x-1)y/5�@�As[6]=(12��2-6��+1)y/7�@�As[8]=(40��3-40��2+18��-3)y/15�@�A
s[10]=(2��-1)(24��3-28��2+20��-5)y/11
�̕����y���ɃX�b�L���ł��B
�@�f�`�h ����̃R�����g�ł��B�i�����Q�V�N�U���P�X���t���j
�@�m���ȑO�A����Ȏ����l�������Ƃ��������ȂƎv���܂������A�ǂ����ďo�������A���v���o
�����Ƃ��Ă��ł��܂���ł����B�m�����낢���J���Ȃ��������߂Ă������L������
������܂��B�����Č����A"�A�C�f�A��"��p�����ł��B
�@�Ƃ���ŁAS(H)�����߂�ꂽ���͕��G�ł����A�R���s���[�^�Ŋm�F���܂��Ƃǂ������
��Ɓ@s[4]�As[6]�A����As[16] �����܂����B���������߂�̂�"�C�f�A��"�𗘗p���ꂽ��
�̂��Ƃł����A�����S�����̊T�O�ɑa���`���v���J���v���ł��B�������A���̈З͂͋���ł�
�邱�Ƃ͊������܂��BS(H)�����̌��ʂ��o���ꂽ�̂͂ƂĂ����Ƃł͗L�蓾���A��
�炩�̃\�t�g�𗘗p���ꂽ�Ɛ������܂��B�����AMathematica�A�������́APARI/GP �̃\�t�g��
���̌v�Z�������邽�߂ɂ́A�ǂ̂悤�ȃR�}���h�ł������\�Ȃ̂��������Ă��������B��
�ꂪ���R���݂Ɏ�ɓ���邱�Ƃ��ł�����A���p�͈͂���C�ɍL���肻���ł��B
�@�r�i�g�j����̃R�����g�ł��B�i�����Q�V�N�U���P�W���t���j
���炢�����܂����B
s[10]=(1/44) (20y - 120���� + 315��2�� - 387��3 + 216����3)
s[12]=(-11056y + 66336���� - 176205��2�� + 226485��3 - 158760����3 + 60480��2��3)/7280
s[14]=(1/320)(2240y - 13440���� + 35805��2�� - 46533��3 + 34344����3 -17280��2��3 + 5184��5)
s[16]=(1/21760)(-925952y + 5555712���� - 14811615��2��
�@�@�@�@�@�@�@�@�@�@+ 19302615��3 - 14429880����3 + 7767360��2��3 - 3058560��5 + 622080����5)
�@�r�i�g�j����̃R�����g�ł��B�i�����Q�V�N�U���P�X���t���j
�@s�F�����̏ꍇ�A�Ⴆ�As[2*3] �́A�@s[6]=(1 + 2n)(1/21)(�� - 6 ��2 + 12��3)
�@�炷���邳��̃R�����g�ł��B�i�����Q�V�N�U���P�X���t���j
�@��=[(9y2)(1/3)/2]�@�i[�@]�̓K�E�X�L���j�Ȃ̂ŁA
s[4]=(6[(9y2)(1/3)/2]-1)y/5
s[6]=(12[(9y2)(1/3)/2]^2-6[(9y2)(1/3)/2]+1)y/7
s[8]=(40[(9y2)(1/3)/2]^3-40[(9y2)(1/3)/2]^2+18[(9y2)(1/3)/2]-3)y/15
s[10]=(2[(9y2)(1/3)/2]-1)(24[(9y2)(1/3)/2]^3-28[(9y2)(1/3)/2]^2+20[(9y2)(1/3)/2]-5)y/11
�̂悤�ɂ͏����܂��B�K�E�X�L�����g�킸�ɁA�������Ō����ɕ\���ƁA
��={{7776y2-1+72y��(11664y2-3)}(1/3)+{7776y2-1-72y��(11664y2-3)}(1/3)-1}/24
�ł�����A������g���K�E�X�L�����g�킸�ɂ������܂��B
�@����āA�Ⴆ�As[4]��y�ŕ\����
s[4]={{7776y2-1+72y��(11664y2-3)}(1/3)+{7776y2-1-72y��(11664y2-3)}(1/3)-5}y/20
�̂悤�ɂȂ�܂��̂ŁA�����炭�ȒP�Ȍ`�ɂ͂Ȃ�Ȃ��ł��傤�ˁB
�@�f�`�h ����̃R�����g�ł��B�i�����Q�V�N�U���P�X���t���j
�@���A���̊Ԃɒm��悵���Ȃ����A�܂����̊W�������邱�Ƃɋ����܂����B
�i�������Q�̊Ԃ̊W����T���Ă�����ł����A�킯�̕�����Ȃ��R�����������o�����Ă��܂����B�j
�@��=[(9y2)(1/3)/2]�@�i[�@]�̓K�E�X�L���j
�@�m���ɁA�R���s���[�^�Ő��l�m�F���Ă����ƁA�s�^���ƈ�v����ł͂���܂��B
�@���́A�K�E�X�L�����g��Ȃ��ꍇ���A��̂ǂ��������Ă��������������܂��A��
����������̂ŁA���������̐��E�œ������Ă�͂�R���s���[�^�Œ����G�v�Z�������Ă݂�
��A���ɂ́A�u29.99999�v�ȂǂǕԂ����Ƃ�����܂����A���̗�ƈ�v������̂��o�����܂����B
�S���z�������Ă��Ȃ��W���Ōq�������̂��Ɠ�x�����܂����B
�@�܂��As[4]�̎������āA����ł͊o���Ă����C�ɂȂ�܂���A��������ȏケ��ɒ��킷
�邱�Ƃ͎��Ԃ̖��ʂł��邱�Ƃ��n�b�L���F���ł��܂����B���������������X�b�L���ƕ���
�̂��ĉ�����̂ŗL���ł��B
�@�炷���邳��̃R�����g�ł��B�i�����Q�V�N�U���P�X���t���j
�@���Ƃ��̊W���́Ay=n(n+1)(2n+1)/6=x(2n+1)/3 ����A
�@9y2=��2(4n2+4n+1)=��2(8��+1)=8��3+��2
�ƂȂ�܂��B�@8��3��8��3+��2��8(x+1)3 ����A8��3��9y2��8(��+1)3�@���A��3��9y2/8��(��+1)3
�@���Ȃ킿�A�@����(9y2)(1/3)/2����+1�@�Ȃ̂ŁA�@��=[(9y2)(1/3)/2]�@�ƂȂ�A�܂��A
�@�@8��3+��2-9y2=0
�Ƃ����O�����������S���S�����������ʂ��A
x={{7776y2-1+72y��(11664y2-3)}(1/3)+{7776y2-1-72y��(11664y2-3)}(1/3)-1}/24
�ł��B
�@�f�`�h ����̃R�����g�ł��B�i�����Q�V�N�U���P�X���t���j
�@���̕�������������A�@��=��(2n+1)/3�@����A�@n=3��/��-1�@�Ƃ���Ă��܂��Ă����B
(n=(3y/��-1)/2 �������I�j
�@������A��=n(n+1)/2�@�֑�������̂ŁA8��3+��2-3��2=0�@�ɂȂ��Ă����B������ꉞ
�R���������ʼn��������i�����̓R���s���[�^�\�t�g�̂����b�ɂȂ����B�j�]��ɂ����G����
�Ȏ����o�������̂ŁA��������|���C�Â����B�ł��v�Z�~�X�����Ȃ��Ă��A���̃K�E�X�L��
�ł���\������Z�͎v���Ă��ł��Ȃ��B
�@�f�`�h ����̃R�����g�ł��B�i�����Q�V�N�U���P�X���t���j
�@�������������̂͋����p�̎��̂����̕��ł����B���Ȃ݂ɁA��p�̏ꍇ�͎��̗l��
���@�ŋ��߂܂����B
�@�P���� (k+1)2-(k-1)2=4k�@���A���ӂ�k2���|���āA�@{(k+1)k}2-{k(k-1)}2=4k3
�@���̎��ɁAk=1�A2�A3�A����An �Ƃ������̂�S�ĉ����āA�@{2s[1]}2=4s[3]
�@����ā@s[3]=s[1]2=x2������@
�@���l�ɁA�@(k+1)3-(k-1)3=2(1+3k2)�@�̗��ӂ�k3���|���āA{(k+1)k}3-{k(k-1)}3=2(k3+3k5)
�@���ꂩ�瓯�l�Ȏ菇�ŁA�@s[3]+3s[5]=4s[1]3=4x3������A
�ȉ��A�����菇��p������グ�Ȃ���i�ނƁA
�@s[5]+s[7]=2s[1]4=2x4������B�@�i���R�r�̊W���Ƃ����炵���B�j
�@s[5]+10s[7]+5s[9]=16x5������C
�@3s[7]+10s[9]+3s[11]=16x6������D
�@s[7]+21s[9]+35s[11]+7s[13]=64x7������E
�@s[9]+7s[11]+7s[13]+s[15]=16x8������F
�@s[9]+36s[11]+126s[13]+84s[15]+9s[17]=256x9������G
�@5s[11]+60s[13]+126s[15]+60s[17]+5s[19]=256x10������H
�@�ȏォ��@���A���B��������H���������ƂŊ�p�̏ꍇ�̌��ʂ��Ax��p���ďo���܂����B
�@������A��������v���O�����ō�Ƃ��܂��ƁA�Q���Ԃ��炢�����Ă���Ă�����Ƃ�2������
���ŕЂÂ��Ă��܂��܂����B
�@���ŋ����p�̏ꍇ���ǂ��������̂�������Ȃ��Ȃ����̂ŁA������v���O�����ŏo��������
�ł��������o�[�W�����̕��������ĉ������B
�@DD++����̃R�����g�ł��B�i�����Q�V�N�U���P�X���t���j
�@���ۂɎ����ĂȂ��̂ŁA�ǂ̒��x�y�ɂȂ邩�킩��܂��An=(m-1)/2 �ƕϊ�����ƌ�
�ʂ��������₷���Ȃ�̂ł́A�Ǝv���܂��B
�@�܂�Ax = n(n+1)/2 = (m2-1)/8 ���A m2 = 8x+1�@�ŁAy = n(n+1)(2n+1)/6 = m(m2-1)/24
�Ƃ��āA������� y�~������ �Ƃ����`�ɂ��āA�c��́Am2 �ɏ�������ďI���B
�@�������Ƃ̌��X�̎�������Ƃ����O��ł����B
�@�f�`�h ����̃R�����g�ł��B�i�����Q�V�N�U���Q�O���t���j
�@�w�����ꂽ�菇�����s���Ă݂܂����B�������A�Ō�ɏo�����ʂ�3/A���|���邱�ƂɂȂ��
���ł����As[4]�`s[10]�܂ŏo���Ă������ʂ����X�Ɍ���Ă��܂����B�R���s���[�^�Ŏ�������
����͂��Ȃ��̂ŁA���\��Ԃ�������܂������A��L�̃e�N�j�b�N�ł��̂������̕��G����
�܂�Ȃ������A���A�� �����̎��ɒu��������Ă����邱�ƂɊ������܂��B
�@�ꉞ�As[20]�܂ł̍�Ƃ��I���܂����̂Ōf�ڂ��Ă݂܂��B�i�~�X���Ă��Ȃ����ȁH�j�Ȃ��A���A
�� �ł͕���킵�������̂ŁAs[1]=n(n+1)/2=A�As[2]=n(n+1)(2n+1)/6=B�@�ɂ��Ă��܂��B
s[4]= (-1+6 A) B/5
s[6]= (1-6 A+12 A^2) B/7
s[8]= (-3+18 A-40 A^2+40 A^3) B/15
s[10]= (-1+2 A) (-5+20 A-28 A^2+24 A^3) B/11
s[12]= (-691+4146 A-9440 A^2+11480 A^3-8400 A^4+3360 A^5) B/455
s[14]= (105-630 A+1436 A^2-1760 A^3+1344 A^4-672 A^5+192 A^6) B/15
s[16]= (-3617+21702 A-49480 A^2+60760 A^3-46880 A^4+24640 A^5-8960 A^6+1920 A^7) B/85
s[18]= (219335-1316010 A+3000668 A^2-3686480 A^3+2851632 A^4
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@-1517376 A^5+583296 A^6-161280 A^7+26880 A^8) B/665
s[20]= (-3666831+22000986 A-50165840 A^2+61638680 A^3-47710320 A^4
�@�@�@�@�@�@�@�@�@�@�@+25465440 A^5-9926400 A^6+2914560 A^7-633600 A^8+84480 A^9)
B/1155
�@�f�`�h ����������܂����B�i�����Q�V�N�U���Q�O���t���j
�@���As[5]=15+25+35+���+1005 ���ǂ����Ă����߂˂Ȃ�Ȃ���ʂɑ��������Ƒz�����Ă�
�悤�B�������A�̂���������As[5]�̌��������������Ƃ͌������Ƃ�������A���̐��m�Ȏ���
�v���o���Ȃ��B�茳�Ɍv�Z�@���R���s���[�^���Ȃ��A����͎̂��Ɖ��M�̂݁B
�@�ܘ_�AS(H)����̕��@�i�Q�l�P�A�Q�l�Q�j�ŁAA[0]=0�Ƃ��炩���ߕ������Ă����Ƃ��Ă��U��
���̘A�����������ƂɂȂ�B���ۏ�L�̕��j�ŃR�c�R�c�i��ł݂��B
�@�܂��A15�A15+25�A15+25+35�A15+25+35+45�A15+25+35+45+65�@�̌v�Z�ƁA�o���オ��U
�̘A����������Ƃ́A���ۂ���Ă݂�ƌ��\�ʓ|�ł���B
�i�R���s���[�^������s��Ń`���`���C�ƍs���܂�������j
�@�����s��ł�낤�Ƃ��Ă��A���Ƃŋt�s����o���͖̂ʓ|�i��肢���@������̂��ȁH�j�B
�@����ɑ���p�̘a�́AS[1]�̒l�݂̂�OK�Ƃ����F����������AS[3]=S[1]2 �͂���
���݂����A(k+1)3-(k-1)3=2+6k ���`�����C�B��́A���ꂩ��As[3]+3s[5]=4s[1]3 ���e�Ղ�������B
�@���m�ɋL�����Ă��Ȃ��Ă��A���̂Q��g�ݍ��킹��A�@s[5]=(4s[1]-1)s[1]2/3
�is[5]=n6/6+n5/2+5n4/12-n2/12=n2(n+1)2(2n2+2n-1) �ɔ�חy���ɊȌ��j
�͗e�Ղɓ���\�B
���R�As[1](n=1�`100)=5050 �Ȃ̂ŁA(4*5050-1)*50502/3=171708332500
�i������1002*1012*(20000+200-1)�̌v�Z���y�H�j
�ŁA�߂ł����߂ł����B
�@���͒f�R����s[5]��n�̎��Ŋo������i�Y��Ă���������̂ɂ������܂��B�j�A�g�C����
s[5]=(4��-1)*��2/3 ��\��t���Ė���ɔ����܂��B
�@�u���莆���p�v�Ƒ肵�āA�f�`�h ����̃R�����g�ł��B�i�����Q�V�N�U���Q�P���t���j
�@�p�X�J���̎O�p�`�ɑ��A�d�ݕt���i���j�O�p�`��
1�@
1�@�@1�A
1�@�@3�A 2�B�@�@�i���@�擪�́u1�v�́A��̒i��1�~�@�A�^�́u3�v�́A��̒i��
�@�@�@�@�@�@�@�@�@�@�@�@�@1�~�@�{1�~�A�A�E�́u2�v�́A��̒i��1�~�A����j
1�@�@7�A�@12�B�@6�C
1�@�@15�A�@50�B�@60�C�@24�D
1�@�@31�A�@180�B�@390�C�@360�D�@120�E
��������������������������������
�ƍ\�����Ă����B
�i��́u180�v�́A��̒i��15*�A+50*�B=30+150����v�Z�A�u390�v�́A50*�B+60*�C=150+240
�@����v�Z�j
�@���̏ォ��U�i�ڂɕ�������p���Ă����W��n�b���ɓ\��t���Ă����B
s[5]=15+25+35+�����+n5
=1*n�b1+31*n�b2+180*n�b3+390*n�b4+360*n�b5+120*n�b6
=n+31*n(n-1)/2+180*n(n-1)(n-2)/6+390*n(n-1)(n-2)(n-3)/24
�@�@�@+360*n(n-1)(n-2)(n-3)(n-4)/120+120*n(n-1)(n-2)(n-3)(n-4)(n-5)/720
=n6/6+n5/2+5n4/12-n2/12
�@����Ȃ�As[19]�As[20]�ł����莆�����őΉ��ł��������B���̏d�ݕt���O�p�`�̌v�Z���A
Mathematica�R�}���h�ŁA
Table[Table[Sum[(-1)^(i+k)*(i+1)^n*Binomial[k,i],{i,0,k}],{k,0,n}],{n,0,10}]//ColumnForm
�ō\���ł��܂����B{n,0,10}�Ȃ�11�i�܂łł��̂�21�i�K�v�Ȃ�{n,0,20}�Ŏ��s�B
�@�X�ɖʔ��������̂��A���̎O�p�`�̐����Əd�݂�g�ݍ��킹��ƁA�x���k�[�C��Bn����
�X�Əo������Ƃ���B
B0=1/�@=1
B1=1/�@-1/�A=1/2 �iB1=-1/2���1�x���k�[�C���AB1=1/2���Q�x���k�[�C���Ƃ����炵���B�j
B2=1/�@-3/�A+2/�B=1/6
B3=1/�@-7/�A+12/�B-6/�C=0
B4=1/�@-15/�A+50/�B-60/�C+24/�D=-1/30
B5=1/�@-31/�A+180/�B-390/�C+360/�D-120/�E=0
B6=1/�@-63/�A+602/�B-2100/�C+3360/�D-2520/�E+720/�F=1/42
��������������������������������
�@���R���̙p��a�ɂ̓x���k�[�C�����Z�b�g�ŏo�����Ă��܂������A����ȕ��ɉB��Ă���
�Ƃ͎v���܂���ł����B��l�����̎d���Ɋ��ӂ��܂��B����Ŗ�����̏ꍇ�ɔ����邽�߂�
�g�C���̒��莆�͂��Ȃ��čς݂܂����B
�i�NjL�j�@�u���R���̙p��a�v�Z����̐i���v�Ƒ肵�āA�f�`�h ����̓��e�ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�V�N�P�O���P�V���t���j
�@���R���̘a�̌���
��k=1�`n k��n(n+1)/2
��k=1�`n k2��n(n+1)(2n+1)/6
��k=1�`n k3��n2(n+1)2/4
��k=1�`n k4��n(n+1)(2n+1)(3n2+3n-1)/30
��k=1�`n k5��n2(n+1)2(2n2+2n-1)/12
�����������������������
�Ȃǂ̎���p���邱�ƂŁA
��k=1�`10 k��55
��k=1�`10 k2��385
��k=1�`10 k3��3025
��k=1�`10 k4��25333
��k=1�`10 k5��220825
����������������������
���v�Z�ł���B
�@�����ŁA�@f(x)=(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9)(x-10)�@�Ƃ����āA��6�Ef�f(��) ��
f(��) �Ŋ����������v�Z����Ɓi�Ȃ��Af�f(��)�͓����j�A
�@10��5+55��4+385��3+3025��2+25333��+220825
�ƁA��L�̈�A�̘a�̒l�����̊e�W���Ƃ��ďo������B���̌����𗘗p����ƁA
�f�� 2�A3�A5�A7�A11�A13�A17�A19 �ɑ���p��a�ł�
�@f(x)=(x-2)(x-3)(x-5)(x-7)(x-11)(x-13)(x-17)(x-19)
�@�@=x8-77x7+2451x6-41817x5+414849x4-2429223x3+8130689x2-14117683x+9699690
�𗘗p���邱�Ƃɂ��Ax11�Ef�f(x)��f(x)�Ŋ����������v�Z���邱�ƂŁA
8x10+77x9+1027x8+15803x7+260167x6+4448507x5+77915887x4
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@+1387350083x3+24995572327x2+454280348267x+8311148375647
���N����̂ŁA
2+3+5+���+17+19=77
2^2+3^2+5^2+���+17^2+19^2=1027
2^3+3^3+5^3+���+17^3+19^3=15803
2^4+3^4+5^4+���+17^4+19^4=260167
2^5+3^5+5^5+���+17^5+19^5=4448507
��������������������������
2^10+3^10+5^10+���+17^10+19^10=8311148375647
����C�ɋ��߂���B
�i�R�����g�j�@�ʔ����v�Z�ł��ˁI
�@f(x)=(x-1)(x-2)(x-3)(x-4)=��4-10��3+35��2-50��+24 �ɂ����āA ��2�Ef�f(��) �� f(��) �Ŋ�������
���v�Z����ƁA�@4��+10
�@���̌W�������āA�@��k=1�`4 �P��4�@�A��k=1�`4 k��10 �Ƃ���̂��ȁH
�@f(x)=(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)=��6-21��5+175��4-735��3+1624��2-1236��+720 �ɂ����āA
�@��4�Ef�f(��)=6��9-105��8+700��7-2205��6+3248��5-1236��4 �� f(��) �Ŋ����������v�Z����ƁA
�@6��3+21��2+91��+441
�@���̌W�������āA
�@�@��k=1�`6 �P��6�@�A��k=1�`6 k��21�@�A��k=1�`6 ��2��91�@�A��k=1�`6 k3��441
�Ƃ���̂��ȁH
�i�NjL�j�@�u�g���������̙p��a�ւ̒���v�Ƒ肵�āA���g�o�����������b�ɂȂ��Ă���g�m
�@�@�@�@�u�f�`�h�v����̓��e�ł��B�i�����Q�W�N�W���V���t���j
�@�g���������v�Z���铹��Ƃ��āAn�br�i��binomial(n�Cr)�j�@�Ȃ�L��������B
�@�悭 n ���Œ肵�� �� ��ω������āA
�@�@n-1�br-1�{n-1�br��n�br�@�An�b0�{n�b1�{n�b2�{����{n�bn���Qn
�Ȃǂ̕ό`�����悭�ڂɂ���B
�@�����ł́A�t�� r ���Œ肵�� n ��ω������邱�Ƃ��l����B
�Ⴆ�Ar��5 �ŌŒ肵�āAn �� 0�`10 �ŕω������a�����A
�@�� ��=0�`10 n�b5�� 1 + 6 + 21 + 56 + 126 + 252 �� 462 �� 11�b6
�܂��Ar=3 �ŌŒ肵�āAn �� 0�`8 �ŕω�������ƁA
�@�� ��=0�`8 n�b3�� 1 +4 +10 +20 +35 +56 �� 126 ��
9�b4
�@��ʂɁA�@�� ��=0�`�� ���b���� n+1�br+1�@����������i*�j
�ƁA�����������b���̘a�����n+1�br+1�̒l�ɑΉ����Ă����B
�@�����ŁA��ʂɁAk2 �� k�b2�Ak�b1�ō���Ă݂�ƁA�@k2���Qk�b2�{k�b1�@���
�@�@�� ��=0�`��k2���Q�� ��=0�`�� k�b2�{�� ��=0�`�� k�b1���Qn+1�b3�{n+1�b2
�@����āA�@���Ӂ��Q(n+1)n(n-1)/6�{(n+1)n/2��n(n+1)(2n+1)/6
���l�ɁA�@��3���Uk�b3�{�Uk�b2�{kC1�@���A
�� ��=0�`����3���U�� ��=0�`�� k�b3�{�U�� ��=0�`�� k�b2�{�� ��=0�`�� kC1
�@�@�@�@�@�@�@���Un+1�b4�{�Un+1�b3�{n+1�b2��n2(n+1)2/4
�ȉ��A
k4��24kC4�{36kC3�{14kC2�{kC1
k5��120kC5�{240kC4�{150kC3�{30kC2�{kC1
k6��720kC6�{1800kC5�{1560kC4�{540kC3�{62kC2�{kC1
k7��5040kC7�{15120kC6�{16800kC5�{8400kC4�{1806kC3�{126kC2�{kC1
�@�@�������
�i�����̌W���͍P�����Ƃ݂�,k=1,2,3,4,����𗼕ӂɑ�����邱�Ƃł�����ɓ���B�j
�𗘗p���邱�ƂŁA���ꂩ�玩�R���̙p��a��g���������̓���Ăō\�����Ă�����B
�i�R�����g�j�@�ʏ�́A�P�����@�i���{�P�j3�|��3���R��2�{�R���{�P�@���g���Ƃ����V�����P����
�@�@��3���Uk�b3�{�Uk�b2�{kC1
���g���킯�ł��ˁI�W���ɂ��ẮA��3����k�b3�{��k�b2�{��kC1 �ɂ����āA
�@�����P�@�Ƃ��āA�@�P����
�@�����Q�@�Ƃ��āA�@�W�����{�Q���@���A�@�����U
�@�����R�@�Ƃ��āA�@�Q�V�����{�R���{�R���@���A�@�����U
�������A��3���Uk�b3�{�Uk�b2�{kC1�@�ł��邱�Ƃ�������B
�@�f�`�h ����̃R�����g�ł��B�i�����Q�W�N�P�P���W���t���j
�@����l�̃z�[���y�[�W�����Ă����牽�C�ɁA
�@�� ��=1�`����5��n+1�b6�{�Q�Un+2�b6�{�U�Un+3�b6�{�Q�Un+4�b6�{n+5�b6
��Ћ��Ɍf�����Ă���A�ŏ��̓f�U�C�����ȂƎv���Ă�����ł����A�v�Z�@�Ŋm�F���Ă݂�
�ƁA���Ƃ��ׂĂ̎��R�����Ńo�b�`���������������Ă���ł͂Ȃ����I
�@����Ȃɂ��ꂢ�Ɏ��R���̙p��a�Ƒg���������Z���ł��邱�Ƃɋ����A��������͂T��
�Ɍ��铙���ł͖����͂����Ƒ��̙p��ŒT���Ă݂܂����B
�@����ƁA
�@�� ��=1�`����4��n+1�b5�{�P�Pn+2�b5�{�P�Pn+3�b5�{n+4�b5
�@�� ��=1�`����3��n+1�b4�{�Sn+2�b4�{n+3�b4
�@�� ��=1�`����2��n+1�b3�{n+2�b3
�@�� ��=1�`������n+1�b2�@�i���ɁA=(n+1)*n/2�j�j
���������Ă����B�����ŁA�㏸�������āA
�@�� ��=1�`����r �ir=6,7,8,9,10,���)
�ł̊W���������Ă݂ĉ������B
�@Seiichi�@Manyama ����̃R�����g�ł��B�i�����Q�W�N�P�P���W���t���j
�@���x�ݒ��Ȃ̂ŁA������ƌ������x�ł����A�I�C���[�������ƊW������̂ł͂Ȃ��ł���
�����H����ɂ���A�uA008292�v����Ȃ��ł��傤���H
�@DD++ ����̃R�����g�ł��B�i�����Q�W�N�P�P���W���t���j
�@n=5 �܂ł������珇�ɍ\�����Ă݂܂��B�܂��́A������O�̓�������o���B
x = x
2x = (x-1)+(x+1) �𗼕ӂɂ����āA2x^2 = (x-1)x + x(x+1)
3x = (x-2)+2(x+1) = 2(x-1)+(x+2) ���e���ɂ����āA
6x^3 = (x-1)x{(x-2)+2(x+1)} + x(x+1){2(x-1)+(x+2)} = (x-2)(x-1)x + 4(x-1)x(x+1)
+ x(x+1)(x+2)
4x = (x-3)+3(x+1) = 2(x-2)+2(x+2) = 3(x-1)+(x+3) ���e���ɂ����āA
24x^4 = (x-2)(x-1)x{(x-3)+3(x+1)} + 4(x-1)x(x+1){2(x-2)+2(x+2)} + x(x+1)(x+2){3(x-1)+(x+3)}
= (x-3)(x-2)(x-1)x + 11(x-2)(x-1)x(x+1)+ 11(x-1)x(x+1)(x+2) + x(x+1)(x+2)(x+3)
5x = �� ���e���ɂ����āA
(5!)x^5 = (x-4)(x-3)(x-2)(x-1)x + 26(x-3)(x-2)(x-1)x(x+1) + 66(x-2)(x-1)x(x+1)(x+2)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ + 26(x-1)x(x+1)(x+2)(x+3) + x(x+1)(x+2)(x+3)(x+4)
�@���āA�����ŁA�e���ɂ���ɁA
6 = (x+1)-(x-5) = (x+2)-(x-4) = (x+3)-(x-3) = (x+4)-(x-2) = (x+5)-(x-1) ��������ƁA
(6!)x^5
= (x-4)(x-3)(x-2)(x-1)x(x+1) - (x-5)(x-4)(x-3)(x-2)(x-1)x + 26(x-3)(x-2)(x-1)x(x+1)(x+2)
�@- 26(x-4)(x-3)(x-2)(x-1)x(x+1) + 66(x-2)(x-1)x(x+1)(x+2)(x+3) - 66(x-3)(x-2)(x-1)x(x+1)(x+2)
�@+ 26(x-1)x(x+1)(x+2)(x+3)(x+4) - 26(x-2)(x-1)x(x+1)(x+2)(x+3) + x(x+1)(x+2)(x+3)(x+4)(x+5)
�@- (x-1)x(x+1)(x+2)(x+3)(x+4)
�@����ɁAx=1,2,3,�c�c,n �������č��v���A6! �Ŋ���ƁA
�@�� ��=1�`����5��n+1�b6�{�Q�Un+2�b6�{�U�Un+3�b6�{�Q�Un+4�b6�{n+5�b6
�@�����ƍ����̎����o��������A6x=�� �������A7x=�� �������A�c�c�A�Ƃ���Ă���ŏI�i
�K�ɓ�������͂��ł��B�����Ƃ��A�ŏI�i�K�����O�ɌW���͑S�������Ă��܂����B
�@����ɖʓ|�Ȃ�A
�@�@A[i,1] = A[i,i] = 1, A[i,j] = (i-j+1)A[i-1,j-1] + jA[i-1,j]
�Ƃ����Q�����ŌW�������v�Z�ł��܂��B
�@�f�`�h ����̃R�����g�ł��B�i�����Q�W�N�P�P���X���t���j
1 1
2;2
1 4 1
3;2 2;3
1 11 11 1
4;2 3;3 2;4
1 26 66 26 1
5;2 4;3 3;4 2;5
1 57 302 302 57 1
�@�@�@�@��������������������
�@57=1*5+26*2�@�A302=26*4+66*3�@�ȂǂƂ����ł��ˁB
�@���̌W�����AEulerian numbers �ƌĂԂ�ł����B�iEluer���Ƃ͂܂��Ⴄ�j�ق��A�P�V�O�O�N
��ł��̊W���������Ă���Ƃ̓I�C���[�͖ʔ����Ă������Ȃ������ł��傤�ˁB��������
�܂Ō����ɖv������C������������Ȃ��͂Ȃ��ł��B�������A����ł��P�R�l���̎q�������
�Ȃ�āA�܂̍C�ł����������ł��B�Ђ���Ƃ��āADD++������q��R�ł́H
�@����=1�`100 ��5 ��101�b6�{�Q�U�E102�b6�{�U�U�E103�b6�{�Q�U�E104�b6�{105�b6=171708332500
�ŃX�C�X�C�v�Z�ł���I��̕��G�ɂȂ�T��ł̌����������Ȃ��Ă����ꂳ������Ώ\
���ł��B
�@DD++ ����̃R�����g�ł��B�i�����Q�W�N�P�P���X���t���j
�@1^5+2^5+3^5+���+100^5=98*99*100*101*102*103/6+5*(100*101/2)^2-4*100*101/2
=171708332500
�̕����A���̏ꍇ�͑��������B
�i�NjL�j�@�����R�O�N�S���Q���t��
�@���w�Z�~�i�[�f�P�W�@�R�����i���{�]�_�Ёj�̂m�n�s�d�ŁA�������s�̃N�X�R���i�X�P�j������
���̘a�̌����̊ȒP�ȏؖ��\����Ă���B�ƂĂ��ȕւȕ��@�Ŋ��������B
�@�r�����P�{�Q�{�R�{�E�E�E�{���@�Ƃ����ƁA�@�r���|�r��-1�����@�ŁA����ɁA
�@�r���{�r��-1���i�P�{�i���|�P�j�j�{�i�Q�{�i���|�Q�j�j�{�E�E�E�{�i�i���|�P�j�{�P�j�{������2
�@����āA�@��3���i�r���|�r��-1�j�i�r���{�r��-1�j���r��2�|�r��-12
�@���������āA�@��k=1�`n ��3���r��2���i��k=1�`n ���j2�@�����藧�B
�i�R�����g�j�@���ȏ����ƁA�i���{�P�j4�|��4 �̍P������p���Ď�����܂����A�ώG�����Ȃ��G��
�@�@�@�@�@�@�K���g�ł��ˁI
�i�NjL�j�@�ߘa�Q�N�V���Q�P���t��
�@�����i���{�P�j�����i���{�P�j�i���{�Q�j/�R�@�������̂ɁA���̂悤�ɊK���^�ɕό`����ƁA�ؖ���
�e�Ղł���B
�@�����i���{�P�j���i�P/�R�j���i���i���{�P�j�i���{�Q�j�|�i���|�P�j���i���{�P�j�j�����i���{�P�j�i���{�Q�j/�R
�i�NjL�j�@�ߘa�S�N�T���Q�V���t��
�@����܂ŁA
�@�P ���� �� �܂ł̎��R���̕����̘a �F �P2�{�Q2�{�E�E�E�{��2 �����i���{�P�j�i�Q���{�P�j/�U
�@�P ���� �� �܂ł̎��R���̗����̘a �F �P3�{�Q3�{�E�E�E�{��3 ����2�i���{�P�j2/�S
�����낢��ȕ��@�Ŏ�����Ă���B�ŋ߁A�ʐς̍l����p�������̂悤�ȏؖ������邱�Ƃ�
�m�����B
�@�܂��A���R���̕����̘a����l���悤�B
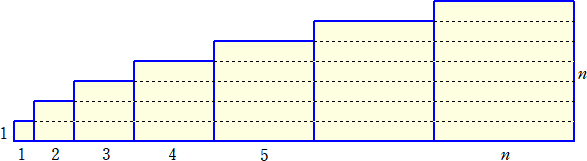
�@��}�̂��̐����`�̖ʐς̑��a���A�@�P2�{�Q2�{�E�E�E�{��2�@�ł���B����������̒���
�`�̖ʐς̑��a�ƍl����B�ʐς̑��a���r�Ƃ���ƁA
�r���i�P�{�Q�{�E�E�E�{���j�{�i�Q�{�R�{�E�E�E�{���j�{�i�R�{�S�{�E�E�E�{���j�{�E�E�E�{��
�@�����i���{�P�j/�Q�{�i���|�P�j�i���{�Q�j/�Q�{�i���|�Q�j�i���{�R�j/�Q�{�E�E�E�{�i���|�i���|�P�j�j�i���{���j/�Q
�@���i��2�{���j/�Q�{�i��2�{���|�Q�j/�Q�{�E�E�E�{�i��2�{��2�|���i���|�P�j�|���i���|�P�j�j/�Q
�@���i��2�{���j/�Q�{�i��2�{���|�Q�j/�Q�{�E�E�E�{�i��2�{���|���i���|�P�j�j/�Q
�@���i��2�{���|�P�E�O�j/�Q�{�i��2�{���|�Q�E�P�j/�Q�{�E�E�E�{�i��2�{���|���i���|�P�j�j/�Q
�@���i��2�{���|�i�P2�|�P�j�j/�Q�{�i��2�{���|�i�Q2�|�Q�j�j/�Q�{�E�E�E�{�i��2�{���|�i��2�|���j�j/�Q
�@�����i��2�{���j/�Q�|�r/�Q�{���i���{�P�j/�S
����āA�@�i�R/�Q�j�r�����i��2�{���j/�Q�{���i���{�P�j/�S�����i���{�P�j�i�Q���{�P�j/�S�@���A
�@�@�r�����i���{�P�j�i�Q���{�P�j/�U
�@���ɁA���R���̗����̘a���l���悤�B
�@�@�@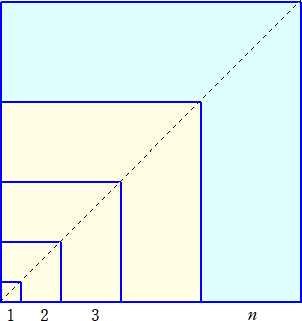
�@��}�̐��F�����̖ʐς́A
�@�@�i�i�P�{�Q�{�E�E�E�{���j�{�i�P�{�Q�{�E�E�E�{�i��-1�j�j�j�����i���i���{�P�j/�Q�{���i��-1�j/�Q�j������3
�Ȃ̂ŁA�����`�S�̖̂ʐς́A�@�P3�{�Q3�{�E�E�E�{��3�@�ł���B
�@�Ƃ���ŁA�����`�̂P�ӂ̒����́A�@�P�{�Q�{�E�E�E�{�������i���{�P�j/�Q�@�Ȃ̂ŁA
�@�P3�{�Q3�{�E�E�E�{��3���i���i���{�P�j/�Q�j2
�����藧�B
�i�NjL�j�@�ߘa�T�N�R���V���t��
�@�ߘa�T�N�x��w���w���ʃe�X�g�ǎ����̐��w�U�E�a�ŁA���R���̕������̘a�Ɋւ����
�肪�o�肳�ꂽ�B����܂łƂ͈قȂ��ŁA�n�b�Ƃ�����ꂽ�B
��Q��m�Q�n�@�P2�{�Q2�{�E�E�E�{�P�O2 ��������̒�ϕ��ŕ\�����Ƃ��l����B���̖₢��
�@�@�@�@�@�@�@������B
�i�P�j�@���ׂĂ̎��� �� �ɑ��āA�@����t+1 �e�i���j��������2�@�ƂȂ�Q�����e�i���j�����߂�B
�i�Q�j�@�P2�{�Q2�{�E�E�E�{�P�O2 ��������̒�ϕ��ŕ\���B
�i���j�i�P�j�@�e�i���j������2�{�����{���@�i�����O�j�@�Ƃ����ƁA
�@����t+1 �e�i���j�������i��/�R�j�i�R��2�{�R���{�P�j�{�i��/�Q�j�i�Q���{�P�j�{������2�@���P�����Ȃ̂ŁA
�@�����P�@�A���{�����O�@�A��/�R�{��/�Q�{�����O
����������āA�@�����P�@�A�����|1�@�A�����P/�U�@���A�@�e�i���j����2�|���{�P/�U
�i�Q�j�@�P2�{�Q2�{�E�E�E�{�P�O2
�@����12 �e�i���j�����{��23 �e�i���j�����{�E�E�E�{��1011 �e�i���j����
�@����111 (��2�|���{�P/�U)�����@�ƕ\�����B�@�@�i�I�j
�i�R�����g�j�@�v�Z����ƁA�@��111 (��2�|���{�P/�U)�������R�W�T�@�ł���B
�@���̖��ݒ肪�ǂ̂悤�Ȕ��W�������炷�̂��A��������Ƃ���ł���B
�i�NjL�j�@�ߘa�T�N�U���Q�X���t��
�@�������̐���̘a�̖����l���Ă݂��B
����@����̘a�@�P�{�P�P�{�P�P�P�{�E�E�E�{�P�P�P�P�P�P�P�P�P�@�����߂�B
�@�v�Z���ʂ́A���R�̂��Ƃ��u�P�Q�R�S�T�U�V�W�X�v�ɂȂ�킯�ł��邪�A�����Ƃ��炵���v�Z����
�݂悤�B
�i���j�@�悎���́A�@�P�{�P�O�{�E�E�E�{�P�O��-1���i�P�O���|�P�j/�X�@�Ȃ̂ŁA
�@�^������k=19 �i�P�O���|�P�j/�X���P�O�i�P�O9�|�P�j/�W�P�|�P���i�P�O10�|�X�P�j/�W�P�@�@�i�I�j
�@��L�̖��Ɏ������āA���̖���ݒ肵���B
����@����̘a�@�P�{�Q�Q�{�R�R�R�{�E�E�E�{�X�X�X�X�X�X�X�X�X�@�����߂�B
�i���j�@�^�����i�P�{�Q�{�E�E�E�{�X�j�{�P�O�i�Q�{�R�{�E�E�E�{�X�j�{�P�O2�i�R�{�S�{�E�E�E�{�X�j�{
�@�@�@�P�O3�i�S�{�T�{�E�E�E�{�X�j�{�P�O4�i�T�{�U�{�E�E�E�{�X�j�{�P�O5�i�U�{�V�{�E�E�E�{�X�j�{
�@�@�@�P�O6�i�V�{�W�{�X�j�{�P�O7�i�W�{�X�j�{�P�O8�E�X
�@�@���X�O�O�O�O�O�O�O�O�{
�@ �@�@�P�V�O�O�O�O�O�O�O�{
�@ �@�@�@�Q�S�O�O�O�O�O�O�{
�@�@�@�@�@ �R�O�O�O�O�O�O�{
�@�@�@�@�@�@ �R�T�O�O�O�O�{
�@�@�@�@�@�@�@ �R�X�O�O�O�{
�@�@�@�@�@�@�@�@ �S�Q�O�O�{
�@�@�@�@�@�@�@�@�@ �S�S�O�{
�@�@�@�@�@�@�@�@�@�@ �S�T
�@�@���P�O�X�V�R�X�R�U�W�T�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�W���Q�T���t��
�@����̘a �r������k=1n ��k �� �s������k=1n ��k2 �ɂ��āA���̓��k��w�@���n�i�P�X�V�X�j��
���͖ʔ����B
��Q���@�@�e�������̓������� ��1�C��2�C�E�E�E�C�����C�E�E�E�@�ɂ����āA
�@�@�r������k=1n ��k�@�A�s������k=1n ��k2 �Ƃ���B�C�ӂ̎��R�����ɑ��āA
�rn����2�{���|�P�A�s�����i�S��3�|���j/�R �����藧�Ƃ��A���̓�������̏����ƌ��������߂�B
�i���j�@��1���r1���P�@�ŁA��12 ���s1���P�@���Ȃ킿�A�@��1���P�@����A�@��1���P
�@����āA���� �� �́A�P�@�ƂȂ�B���������Ƃ����B
�@�r�������i�Q�{�i���|�P�j���j/�Q����2�{���|�P�@����A
�@�i���|�Q�j��2�|�����{�Q���O�@���Ȃ킿�A�@�i�i���|�Q�j���|�Q�j�i���|�P�j���O
�����P�@���A�@�i���|�Q�j���|�Q���O�@�Ȃ̂ŁA�@�����Q�{�Q/��
�� �� ���@�̂Ƃ��A�@�����Q
�܂��A�@�P�{�i�P�{���j2���P�O�@���A�@�P�{�����R�@���Ȃ킿�A�@�����Q
����āA�����Q�@�łȂ���Ȃ�Ȃ��B
�@�t�ɁA�����P�A�����Q�@�̂Ƃ��A
�@�r������2�@�ŁA���炩�ɁA�@�rn����2�{���|�P�@�����藧�B
�@�s������k=1n �i�Q���|�P�j2 ���i�Q/�R�j���i���{�P�j�i�Q���{�P�j�|�Q���i���{�P�j�{�����i�S��3�|���j/�R
���A�@�s�����i�S��3�|���j/�R �����藧���A���������B
�@�ȏォ��A���߂铙������̏����͂P�ŁA�����͂Q�ł���B�@�@�i�I�j
�@kuiperbelt ����̃R�����g�ł��B�i�ߘa�U�N�W���Q�U���t���j
�@����̘a
��_{k=1�`n}k=n(n+1)/2=C(n+1,2)
��_{k=1�`n}k(k+1)=n(n+1)(n+2)/3=2C(n+2,3)
��_{k=1�`n}k(k+1)(k+2)=(1/4)��_{k=1�`n}k(k+1)(k+2)(k+3)-(k-1)k(k+1)(k+2)=n(n+1)(n+2)(n+3)/4=3!C(n+3,4)
��_{k=1�`n}k(k+1)(k+2)(k+3)(k+4)=(1/5)��_{k=1�`n}k(k+1)(k+2)(k+3)(k+4)-(k-1)k(k+1)(k+2)(k+3)
=n(n+1)(n+2)(n+3)(n+4)/5=4!C(n+4,5)
�@�E�E�E�E�E�E
��_{k=1�`n}k(k+1)(k+2)(k+3)(k+4)...(k+m-1)=(m-1)!C(n+m-1,m)
�ƁA
C(n,k)=C(n-1,k)+C(n-1,k-1)�@���AC(n-1,k-1)=C(n,k)-C(n-1,k)�@����A
C(n,k)=C(n+1,k+1)-C(n,k+1)=C(n+2,k+2)-2C(n+1,k+2)+C(n,k+2)
=C(n+3,k+3)-3C(n+2,k+3)+3C(n+1,k+3)-C(n,k+3)
=��_{j=0�`m}(-1)^j*C(m,j)*C(n+m-j,k+m)
���A
��_{k=1�`n}k^2=��_{k=1�`n}k(k+1)-��_{k=1�`n}k
=2C(n+2,3)-C(n+1,2)=2C(n+2,3)-(C(n+2,3)-C(n+1,3))=C(n+2,3)+C(n+1,3)
��_{k=1�`n}k^3=��_{k=1�`n}k(k+1)(k+2)-3��_{k=1�`n}k(k+1)+��_{k=1�`n}k
=3!C(n+3,4)-3*2C(n+2,3)+C(n+1,2)
=6C(n+3,4)-6C(n+2,3)+C(n+1,2)
=6C(n+3,4)-6(C(n+3,4)-C(n+2,4))+C(n+3,4)-2C(n+2,4)+C(n+1,4)
=C(n+3,4)+4C(n+2,4)+C(n+1,4)
��_{k=1�`n}k^4
=��_{k=1�`n}k(k+1)(k+2)(k+3)-6��_{k=1�`n}k(k+1)(k+2)+7��_{k=1�`n}k(k+1)-��_{k=1�`n}k
=4!C(n+4,5)-6*3!C(n+3,4)+7*2C(n+2,3)-C(n+1,2)
=24C(n+4,5)-36C(n+3,4)+14C(n+2,3)-C(n+1,2)
=24C(n+4,5)-36(C(n+4,5)-C(n+3,5))+14(C(n+4,5)-2C(n+3,5)+C(n+2,5))-(C(n+4,5)-3C(n+3,5)+3C(n+2,5)-C(n+1,5))
=C(n+4,5)+11C(n+3,5)+11C(n+2,5)+C(n+1,5)
��_{k=1�`n}k^5
=��_{k=1�`n}k(k+1)(k+2)(k+3)(k+4)-10��_{k=1�`n}k(k+1)(k+2)(k+3)+25��_{k=1�`n}k(k+1)(k+2)
-15��_{k=1�`n}k(k+1)+��_{k=1�`n}k
=5!C(n+5,6)-10*4!C(n+4,5)+25*3!C(n+3,4)-15*2C(n+2,3)+C(n+1,2)
=120C(n+5,6)-240C(n+4,5)+150C(n+3,4)-30C(n+2,3)+C(n+1,2)
=120C(n+5,6)-240(C(n+5,6)-C(n+4,6))+150(C(n+5,6)-2C(n+4,6)+C(n+3,6))
-30(C(n+5,6)-3C(n+4,6)+3C(n+3,6)-C(n+2,6))+(C(n+5,6)-4C(n+4,6)+6C(n+3,6)-4C(n+2,6)+C(n+1,6))
=C(n+5,6)+26C(n+4,6)+66C(n+3,6)+26C(n+2,6)+C(n+1,6)
��_{k=1�`n}k^6
=��_{k=1�`n}k(k+1)(k+2)(k+3)(k+4)(k+5)-15��_{k=1�`n}k(k+1)(k+2)(k+3)(k+4)
+65��_{k=1�`n}k(k+1)(k+2)(k+3)-90*��_{k=1�`n}k(k+1)(k+2)
+31*��_{k=1�`n}k(k+1)-��_{k=1�`n}k
=6!C(n+6,7)-15*5!C(n+5,6)+65*4!C(n+4,5)-90*3!C(n+3,4)+31*2C(n+2,3)-C(n+1,2)
=720C(n+6,7)-1800C(n+5,6)+1560C(n+4,5)-540C(n+3,4)+62C(n+2,3)-C(n+1,2)
=C(n+6,7)+57C(n+5,7)+302C(n+4,7)+302C(n+3,7)+57C(n+2,7)+C(n+1,7)
�@Dengan kesaktian Indukmu ����̃R�����g�ł��B�i�ߘa�U�N�W���Q�V���t���j
�@��ׂĂ݂���ƂĂ������[�������ł��B�i���@�����ʐM�j
�i�R�����g�j�@���k��w�@���n�i�P�X�V�X�j�@�ŁA���̖�肪�o�肳��Ă���Bkuiperbelt ����̓�
�@�@�@�@�e��q�����āA���̖��̏d�v�����q�V�q�V�Ɗ������܂����B
����@�@�r������k=1n ���@�i�����P�A�Q�A�E�E�E�j�@�Ƃ���Ƃ��A���̘a�����߂�B
�i�P�j�@�s������k=1n �rk
�i�Q�j�@�t������k=1n �sk
�i���j�@�r�������i���{�P�j/�Q�@����A
�i�P�j�@�s�����i�P/�Q�j��k=1n ���i���{�P�j���i�P/�U�j���i���{�P�j�i���{�Q�j
�i�Q�j�@�t�����i�P/�U�j��k=1n ���i���{�P�j�i���{�Q�j���i�P/�Q�S�j���i���{�P�j�i���{�Q�j�i���{�R�j�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�O���Q�U���t��
�@���̓��k��w�@���n�i�P�X�W�R�j�̖��������[���B
����@�@�i�P�j�@�e�i���j�� �� �̂S�����ŁA�C�ӂ̎��� �� �ɑ��ā@��x-1x �e�i���j��������4�@����
�@�@�Ƃ����B�e�i���j�����߂�B
�i�Q�j�@�i�P�j�𗘗p���ā@��k=1n ��4�@�����߂�B
�i���j�i�P�j�@�e�i���j������4�{����3�{����2�{�����{���@�Ƃ����ƁA�������A
�i��/�T�j�i��5�|�i���|�P�j5�j�{�i��/�S�j�i��4�|�i���|�P�j4�j�{�i��/�R�j�i��3�|�i���|�P�j3�j�{�i��/�Q�j�i��2�|�i���|�P�j2�j�{��
���i��/�T�j�i�T��4�|�P�O��3�{�P�O��2�|�T���{�P�j�{�i��/�S�j�i�S��3�|�U��2�{�S���|�P�j
�@�{�i��/�R�j�i�R��2�|�R���{�P�j�{�i��/�Q�j�i�Q���|�P�j�{��
������4�{�i�|�Q���{���j��3�{�i�Q���|�R��/�Q�{���j��2�{�i�|���{���|���{���j���{��/�T�|��/�S�{��/�R�|��/�Q�{��
����4�@�� �� �̍P�����Ȃ̂ŁA
�@�����P�@�A�|�Q���{�����O�@���A�����Q�@�A�Q���|�R��/�Q�{�����O�@���A�����P
�@�|���{���|���{�����O�@���A�����O�@�A��/�T�|��/�S�{��/�R�|��/�Q�{�����O�@���A�����|�P/�R�O
�ȏォ��A�@�e�i���j����4�{�Q��3�{��2�|�P/�R�O�@�ł���B
�i�Q�j�@��k=1n ��4����0n �i��4�{�Q��3�{��2�|�P/�R�O�j��������5/�T�{��4/�Q�{��3/�R�|��/�R�O�@�@�i�I�j
�i�R�����g�j�@���������܂Ŋ撣��A
�@��5/�T�{��4/�Q�{��3/�R�|��/�R�O
�����i�U��4�{�P�T��3�{�P�O��2�|�P�j/�R�O
�����i���{�P�j�i�U��3�{�X��2�{���|�P�j/�R�O
�����i���{�P�j�i�Q���{�P�j�i�R��2�{�R���|�P�j/�R�O
�ƂȂ�܂��ˁI�ł��A�����܂ŋ��߂�A�Ƃ��w������Ă��Ȃ��̂ŁD�D�D�B
�i�NjL�j�@�ߘa�U�N�P�O���Q�X���t��
�@���̓��k��w�@�������ʁi�P�X�W�S�j�̖��́A�s�����̕]���Ɋւ�����ł���B
���Q�@�@����o�����p�ɂ����āA�������O �i�����P�A�Q�A�E�E�E�j�Ƃ��A��������k=1n ���� �Ƃ����B���̂�
�@�@���A���̕s�����𐔊w�I�A�[�@��p���ďؖ�����B
�@(�P�{��1)(�P�{��2)�E�E�E (�P�{����)���P�{�����{����2/�Q�I�{�E�E�E�{������/���I
�i���j�@�����P�@�̂Ƃ��A���Ӂ��P�{��1�@�A�E�Ӂ��P�{��1���P�{��1�@�Ȃ̂ŁA���Ӂ��E��
�@����āA�����P�@�̂Ƃ����藧�B
�������i�����P�j�@�̂Ƃ��A���藧�Ɖ��肷��B���Ȃ킿�A
�@(�P�{��1)(�P�{��2)�E�E�E (�P�{����)���P�{�����{����2/�Q�I�{�E�E�E�{������/���I
���̂Ƃ��A�@
(�P�{��1)(�P�{��2)�E�E�E (�P�{����) (�P�{����+1)���P�{����+1�{����+12/�Q�I�{�E�E�E�{����+1��+1/(���{�P�j�I
�����藧���Ƃ������B
�@�P�{����+1�{����+12/�Q�I�{�E�E�E�{����+1��+1/(���{�P�j�I�@�ɂ����āA
�����P�A�Q�A�E�E�E�A���{�P�@�ɑ���
�@����+1��/���I���i�����{����+1�j��/���I���i�������{��������-1����+1�j/���I
�Ȃ̂ŁA
�P�{����+1�{����+12/�Q�I�{�E�E�E�{����+1��+1/(���{�P�j�I
���i�P�{�����{����2/�Q�I�{�E�E�E�{������/���I�j�{����+1�i�P�{�����{����2/�Q�I�{�E�E�E�{������/���I�j
��(�P�{��1)(�P�{��2)�E�E�E (�P�{����)�{����+1(�P�{��1)(�P�{��2)�E�E�E (�P�{����)
��(�P�{��1)(�P�{��2)�E�E�E (�P�{����) (�P�{����+1)
�@����āA�������{�P�@�̂Ƃ������藧�B
���������āA���ׂĂ̎��R�����ɑ��āA�s�����͐��藧�B�@�@�i�I�j
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�P�P���R���t���j
�@����ȉ��������v�������ꍇ�A�ǂ����������ł��傤�ˁB
�i�ʉ��j�@�C�ӂ̎��R�� k �ɑ� 1+a[k]��0 �Ȃ̂ŁA�������ςƑ��敽�ς̑召�W�ɂ��A
�@�o(�P�{��1)�{(�P�{��2)�{�E�E�E�{ (�P�{����)�p/�����o(�P�{��1)(�P�{��2)�E�E�E (�P�{����)�p�O�i�P/���j
���Ȃ킿�A�@��[k=1��n] (1+a[k]) �� (1+s[n]/n)^n = ��[k=0��n] nCk/n^k*s[n]^k
�����ŁAnCk/n^k * k! = nPk/n^k �� 1 �Ȃ̂ŁAnCk/n^k �� 1/k!
���������āA��[k=1��n] (1+a[k]) �� ��[k=0��n] s[n]^k/k!�@�@�i�I�j
�����w�I�A�[�@���g�������{���𑨂����ؖ��ł͂Ȃ����Ǝv���܂����A�A�[�@���g���Ă�
�@���̂� 0 �_�ɂȂ��ł��傤���H
�@�ؖ��@�̒T���̏ꍇ�͂��Ă����A�����ŏؖ����@�ɐ���������̂́A�i���Z���X�Ɗ���
�܂��ˁB
�i�R�����g�j�@�����ȏؖ��ŁA�������܂����IDD++ ����Ɋ��ӂ��܂��B�����A�ؖ����@�ɐ���
�@�@�@�@�@�����Ă���̂ŁA���_�͖Ƃ�Ȃ������D�D�D�B
�i�NjL�j�@�ߘa�V�N�P�O���P���t��
�@���̓��k��w�@�O�����n�i�Q�O�O�O�j�̖��́A���������Ə��������Ɋւ�����ł���B
����@�@����o��n�p�������S/�T�A����Q�̓��䐔��A����o��n�p�������P/�T�A����|�P/�Q��
�@�@���䐔��Ƃ���B
�i�P�j�@�����P�A�Q�A�R�A�S�A�T�̂Ƃ��A��n�̏������������߂�B
�i�Q�j�@an����n�{��n �̏���������n�����߂�B
�i�R�j�@����o��n�p�̏��������P�O�O���܂ł̘a�̐������������߂�B
�i���j�i�P�j�@��1���S/�T���O�D�W�@�A��2���W/�T���P�{�O�D�U�@�A��3���P�U/�T���R�{�O�D�Q�@�A
�@��4���R�Q/�T���U�{�O�D�S�@�A��5���U�S/�T���P�Q�{�O�D�W�@���A�����P�A�Q�A�R�A�S�A�T�̂Ƃ��A
��n�̏��������́A�@�O�D�W�@�A�O�D�U�@�A�O�D�Q�@�A�O�D�S�@�A�O�D�W�@�ł���B
�i�Q�j�@�i�P�j���A��n�̏��������́A�O�D�W�@�A�O�D�U�@�A�O�D�Q�@�A�O�D�S�@�A�O�D�W�@�������J��Ԃ��B
�܂��A��n���i�P/�T�j�E�i�|1/�Q�jn-1 �ŁA��1���P/�T�@���Aa1����1�{��1���P�@�ƂȂ�A ��1���O
�����Q�@�̂Ƃ��A��n���P�A�|�O�D�P����n���O�D�P �Ȃ̂ŁAan����n�{��n �̏���������n �́A
��n�̏��������ƃ�n �̘a�ɓ������B
����āA�����P�A�Q�A�R�A�E�E�E�@�ɂ��āA
�����S���|�R�@�̂Ƃ��A��n���S/�T�{�i�P/�T�j�E�i�|1/�Q�j4k-4���i�S�{�i1/�Q�j4k-4�j/�T�@�������A�����P
�����S���|�Q�@�̂Ƃ��A��n���i�R�|�i1/�Q�j4k-3�j/�T
�����S���|�P�@�̂Ƃ��A��n���i�P�{�i1/�Q�j4k-2�j/�T
�����S���@�̂Ƃ��A��n���i�Q�|�i1/�Q�j4k-1�j/�T
�i�R�j�@��n=1100 ��n
���i�P/�T�j�i��k=225 �i�S�{�i1/�Q�j4k-4�j�{��k=125 �i�R�|�i1/�Q�j4k-3�j
�@�{��k=125 �i�P�{�i1/�Q�j4k-2�j�{��k=125 �i�Q�|�i1/�Q�j4k-1�j)
���i�P/�T�j�i�Q�S�U�{�i�P�|�P/�Q�{�P/�S�|�P/�W�j��k=125 �i1/�Q�j4k-4�|1�j
���i�P/�T�j�i�Q�S�U�{�i�T/�W�j��k=125 �i1/�Q�j4k-4�|1�j
���i�P/�T�j�i�Q�S�U�{�i�T/�W�j�i�P�U/�P�T�j�i�P�|�i1/�Q�j100)�|1�j
���S�X�{�i�Q/�P�T�j�i�P�|�i1/�Q�j100)
�@�O���i�Q/�P�T�j�i�P�|�i1/�Q�j100)���P�@�Ȃ̂ŁA��n=1100 ��n �̐��������́A�S�X�B�@�@�i�I�j
�i�R�����g�j�@������n�[�h�Ȍv�Z�ł����B��肭�v�Z���Ȃ��Ƒ�ςł��B
�@�@�ȉ��A�H����

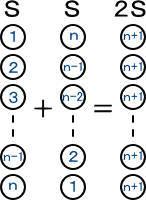




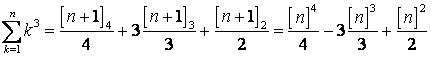 �@�@�i�X�^�[�����O�j
�@�@�i�X�^�[�����O�j
