
当ホームページは、平成14年5月23日(木)より「数学博物館展示室」に出陳されている。
数学博物館に展示されていることのシンボルとして、九点円アイコン(下図)を、各ホームペ
ージのトップページに貼り付けることになっている。
![]()
このページでは、九点円について紹介したい。
△ABCにおいて、
3辺の中点、、各頂点から下ろした垂線の足、垂心と各頂点を結ぶ線分の中点
の合計9点は、同一円周上にある。この円のことを、九点円という。
九点円は、オイラー円とかフォイエルバッハ円とも呼ばれる。
九点円の中心は、外心と垂心を結ぶ線分の中点で、九点円の半径は、外接円の半径
の半分
である。
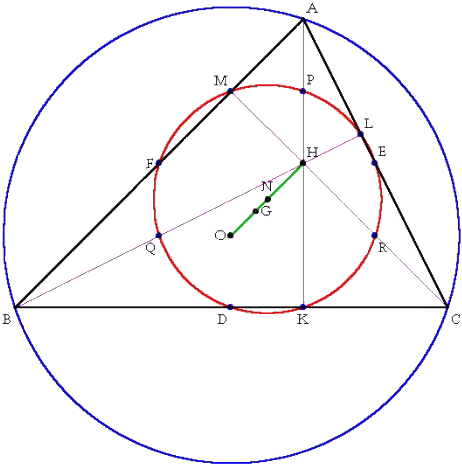 |
O:外心 G:重心 H:垂心 N:九点円の中心 |
4点O,G,N,Hは同一直線上にある。この直線のことを、オイラー線という。線分の比は、
OG:GN:NH=2:1:3
となる。
九点円が上記のような性質を何故もつのか?その理由は簡単である。
∠PKD=90°より、点Kは線分PDを直径とする円周上にある。他も同様。このことから、
九点円のもつ性質は、明らかとなる。
実際に、O(0)、A( α )、B( β )、C( γ )とする。但し、複素数 α 、 β 、 γ の絶対
値は 1 とする。すなわち、△ABCの外接円は単位円であるものとする。
このとき、 D(( β + γ )/2 ) 、 P({ α +( α + β + γ
)}/2 ) なので、線分DP
の中点を N(n) とすると、 n=( α + β + γ )/2 となる。
よって、線分DPの中点 N は、外心Oと垂心Hを結ぶ線分の中点である。
さらに、 PN=(1/2)|α|=1/2 が成り立つので、九点円の半径は、外接円の半径
の半分である。 同様にして、(E、Q、L)や(F、R、M)についても同じことがいえる。
また、G(( α + β + γ )/3 )、H( α + β + γ ) なので、
OG : GN : NH = 2 : 1 : 3
が成り立つ。
(コメント) 平面幾何の有名事実も、複素数を使うと、易しく思えてくるから不思議です。
九点円については、次のような定理も知られている。1822年にフォイエルバッハが証明
したという。
フォイエルバッハ(Feuerbach)の定理
三角形の内接円は九点円に内接し、傍接円は九点円に外接する
(参考文献:石谷 茂 著 複素数とベクトル(東京図書))
寺阪英孝編 現代数学小事典によれば、フォイエルバッハの定理の証明は相当むずかし
いという。そんなわけで何となく証明の全貌を探訪したくなった。(平成22年3月19日付け)
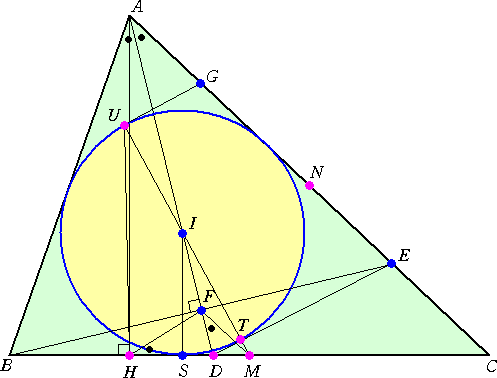
(証明) 辺BC、辺ACの中点をそれぞれM、Nとし、頂点Aより辺BCに下ろした垂線の足を
Hとする。△ABCの内心を I とし、∠Aの2等分線AI が辺BCと交わる点をDとおく。
AB=ACの2等辺三角形ABCにおいては、M=H=D で、内接円が辺BCの中点Mで九
点円に内接することは明らかである。
そこで、一般性を失うことなく、辺AB<辺ACとしてよい。
△ABCにおいて、点Dから内接円 I に接線を引き、接点をT、辺ACとの交点をEとする。さ
らに、線分BEと線分ADの交点をFとする。
△ABDと△AEDにおいて、
AD共通 、 ∠BAD=∠EAD 、 ∠ADB=∠ADE
より、 △ABD≡△AED なので、 AB=AE となる。
このことから、△ABFと△AEFにおいて、
AF共通 、 AB=AE 、 ∠BAF=∠EA
より、 △ABF≡△AEF なので、 AF⊥BE かつ、Fは線分BEの中点となる。
このとき、内接円 I と辺BCとの接点をSとして、中点連結の定理より、FMとECは平行で、
2FM=EC=AC−AE=AC−AB=SC−SB=SM+MC−BM+SM=2SM より、
FM=SM が成り立つ。
また、F、HはABを直径とする円周上の点より、∠BAD=∠FHM で、さらに、FMとEC
は平行であることから、 ∠DFM=∠DAC より、 ∠FHM=∠DFM
よって、△FHM∽△DFM より、 HM : FM = FM : DM なので、 FM2=HM・DM
すなわち、 SM2=HM・DM が成り立つ。
ここで、直線MTが内接円 I と交わる点をUとおく。(線分UMが I を通るとは限らない!)
このとき、方べきの定理より、 SM2=MT・MU となる。
したがって、 HM・DM=MT・MU が成り立つので、方べきの定理の逆より、
4点H、D、T、Uは同一円周上にある。
このとき、 ∠HUM=∠TDM=∠ABC−∠ACB
また、Nは直角三角形AHCの斜辺ACの中点なので、NH=NC で、∠NHC=∠ACB
ここで、 NMとABは平行なので、∠NMC=∠ABC
このとき、 ∠HNM=∠NMC−∠NHM=∠ABC−∠ACB なので、
∠HUM=∠HNM
したがって、円周角の定理の逆より、 4点H、M、N、Uは同一円周上にあることが分かり、
さらに、Sは九点円の周上の点である。
そこで、点Uにおける内接円 I の接線が辺ACと交わる点をGとすると、
∠GUM=∠ETU=∠UHM
なので、線分UGは九点円に接する。
以上から、△ABCの内接円と九点円はSで接する。
傍接円についても同様である。(証明は読者の方にまかせよう。) (証終)
(コメント) なかなか込み入った証明ですね!最後は接弦定理の逆を用いて、その鮮やか
さに感動しました。
(参考文献: 矢野健太郎 監修 清宮俊雄 著 モノグラフ 幾何学 (科学新興社))
(追記) 平成22年3月12日付け
平成22年2月26日付けで、HN「FN」さんが、当HPの掲示板「出会いの泉」に次のような
質問を書き込まれた。
オイラーが膨大な計算で証明している次の事実 :
三角形の内心がオイラー線上にあれば二等辺三角形である
これを初等幾何で証明することは可能でしょうか。
(コメント) 入試選抜業務の真っ只中で、忙しさの余りレスすることもできず、FNさんには
失礼しました。でも、平成22年3月12日付けで、自己解決されたとの報告を伺
って、安心しました。
以下では、FNさんの解答を紹介したいと思う。(一部文言等修正させていただきました。)
次の定理を用いると容易に示される。
定 理 △ABCの外心をO、垂心をH、内心をIとするとき、AIは∠OAHを2等分する
外心と垂心は等角共役であるともいい、よく知られた事実らしい。
証明は易しい。
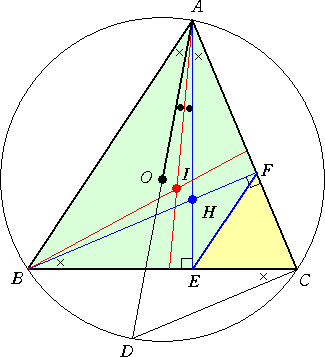
(証明) 左図において、
4点A、B、E、Fは同一円周上にあ
るので、 ∠EBF=∠EAF
また、BFとDCは平行なので、
∠BCD=∠EBF
さらに、 ∠BAD=∠BCD
以上から、 ∠BAD=∠EAF
AI は∠Aの2等分線なので、AI は
∠OAHを2等分する。 (証終)
この定理を用いて、
三角形の内心がオイラー線上にあれば二等辺三角形である
という事実が次のように示される。
(証明) オイラー線が△ABCの頂点を通る場合、2等辺三角形になることは明らか。
オイラー線が△ABCの頂点を通らない場合を考える。
AI が∠OAHを2等分するので、 OA : AH = OI : IH
BI が∠OBHを2等分するので、 OB : BH = OI : IH
同様にして、 OC : CH = OI : IH
従って、 OA : AH = OB : BH = OC : CH
ところが、 OA=OB=OC だから、 AH=BH=CH
これは、Hが外心であることを示し、O=H となるので正三角形になる。
よって、この場合も2等辺三角形になると言える。 (証終)
(コメント) 定理が効果的に使われていますね!FNさんに感謝します。
上記の証明に関連して、次の事実が知られている。
三角形の内心、外心、垂心、重心の4つのうち2つが一致するならば、その三角形
は正三角形である
ここで、等角共役についてまとめておこう。
△ABCの頂角Aを通る直線を m とし、∠Aの2等分線に関して、m と対称な直線を
n と
するとき、m と n は互いに等角共役線であるという。
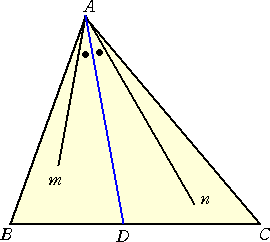
さらに、各頂点を通る直線が 1点 P で交わるとき、それらの等角共役線も
1点 Q で交わ
る。このとき、点 P と点 Q は互いに等角共役点という。
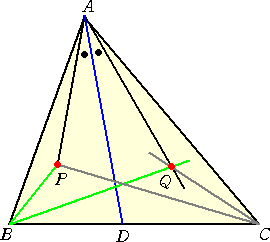
また、次の3条件
∠PAB=∠CAQ 、 ∠PBC=∠ABQ 、 ∠PCA=∠BCQ
を満たすときも、点 P と点 Q は互いに等角共役点という。
角度に関する条件なので、2点が等角共役点かどうかを判別する場合は、こちらの方が
有用かもしれない。
 実際に、左図において、
実際に、左図において、
∠OAB=∠CAH
∠OBC=∠ABH
∠OCA=∠BCH
が成り立つので、
△ABCにおいて
外心と垂心は等角共役点
であると言える。