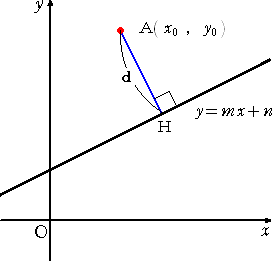点と直線の距離 
平面上の図形問題で、「点と直線の距離」の公式は、絶大なる力を発揮する武器として、
受験生は、必ず身につけなければならない必須技法だろう。その割には、以前の学習指
導要領に比べて、その扱いは軽減されているように感じる。
公式は、単純である。
点A( x0 , y0 ) から、直線 L : ax+by+c=0 に下ろした垂線の長さ d は、
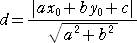
で与えられる。
通常、ベクトルを用いる証明が最短だろう。(ベクトルを太字で表すことにする。)
垂線の足を、H( x , y ) とすると、 AH と ( a , b ) は平行なので、
OH=OA+t・( a , b )
また、点Hは、直線 L 上にあるので、 OH・( a , b )+c=0
よって、 (OA+t・( a , b ))・( a , b )+c=0 より、
OA・( a , b )+t(a2+b2)+c=0
ここで、 a2+b2≠0 なので、
t=−(OA・( a , b )+c)/(a2+b2)=−( ax0 +by0+c )/(a2+b2)
したがって、 d=|AH|=|OH−OA|=|t・( a , b )|
上式に、t の値を代入して、
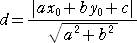
が得られる。
教科書等でこの証明を見る度に辟易するのは私だけであろうか?非常に有用な公式に
もかかわらず、教科書の本文にも入れてもらえない不憫さもあるが、何とか分かりやすい
証明で、その後の応用に期待を持たせるような方法はないものかと模索してきた。
生徒達は、直線というと、「 y=mx + n 」と言うくらいに、この形に馴染んでいる。むしろ
中学校では、「x=a」という形は多分学習していないので当然かもしれないが...。
点と直線の距離の公式も、むしろ生徒達の慣れ親しんだ直線の方程式を用いた方がより
平易な証明になるようだ。予備知識のレベルは、中学3年程度だろう。
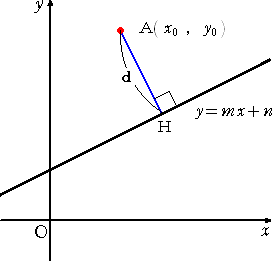 |
直線 y=mx + n とその上にない点
A ( x0 , y0 ) から直線に下ろした垂線
の長さ d は、
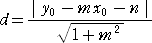
で与えられる。
この値 d が、「点と直線の距離」といわ
れるものである。 |
この公式の証明は種々考えられるが、最近、次のような証明があることを知った。
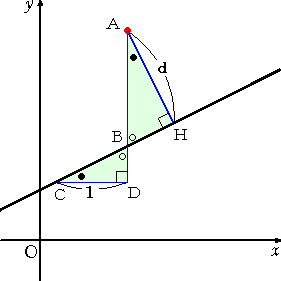 |
左図において、 △ABH ∽ △CBD
なので、 AB : AH = CB : CD
よって、BD = m なので、
| y0 − (mx0 + n) | : d =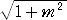 : 1 : 1
より、
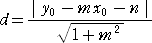
が成り立つ。 |
この形から、直線の一般形の場合の公式を作ることは易しい。
直線 L : ax+by+c=0 において、
b≠0 のとき、 y=−(a/b)x−c/b である。
よって、上記の公式で、 m=−(a/b) 、n=−c/b を代入して計算すれば直ちに、
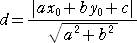
が得られる。
b=0 のとき、点A( x0 , y0 ) から、直線 L : x=−c/a に下ろした垂線の長さ d は、
d=| x0+c/a|=| ax0+c|/|a|
で与えられる。これは、
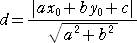
が、 b=0 のときも成り立つことを示す。
以上で、一般の場合が証明された。
(コメント) 問題作成で、直線の方程式を一般形で与えることはあまりしない。初学者にい
たずらな困難さを与えないためである。
ただ、大学入試の問題を見ると、点と直線の距離の公式を使わせる問題は、親心からだ
ろうか、なぜか一般形で与えられることが多い。
一般形の場合の公式に慣れ親しんでいるので、私なども、たとえば、y=2x+3 から、わざ
わざ 2x−y+3=0 と書き直して公式を使っていたりなんかする。
上記の証明を見て分かるように、点と直線の距離の公式は、「y=mx + n」の形の場合が
格段に易しい。なぜ、このような証明が教科書に採用されないのか、とても不思議である。
今まで、直線の一般形の場合を、ベクトル方程式を用いたり、垂線の足Hの座標を直接
的に求めたりなどして証明してきたが、上記の証明をみると、そういう証明は、「とてつもな
く難しい」と感じるのは、私だけだろうか? 是非、この証明を広めたいものだ。
(追記) 平成30年8月4日付け
本日数学に関する会合があり、その席で長岡亮介先生から高校数学の憂うべく現状の話
を伺った。
点と直線の公式は、その有用性から教科書には必ず載っているものだが、その証明は、
日本ではほとんど行われていないとのことである。私自身を振り返っても、教科書の本文に
入っていないということもあり、結果だけを述べて後は使い方を練習するのみであった。
大いに反省し、今後は証明とじっくり向き合わせる教育をしなければと思う一日だった。