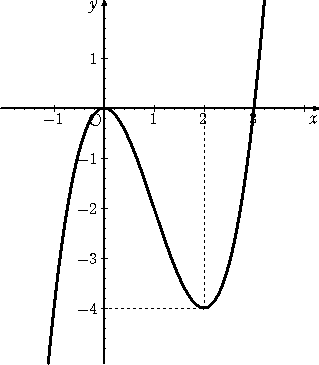変曲点の性質　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　３次関数 ｙ＝ａｘ³＋ｂｘ²＋ｃｘ＋ｄ　の増減・極値を調べて、そのグラフを描くことは、「数
学ＩＩ」における最も重要な学習項目のうちの一つである。

　ただ残念なのは、概形の把握のみに終始し、そのグラフの特徴を詳しく学ぶためには、
「数学ＩＩＩ」を待たなければならないということである。

　もっとも、実際の授業では、その美しい性質と重要性に鑑みて、「数学ＩＩ」の発展として
先取りして教えられる場合が多いかもしれない。

例　３次関数 ｙ＝ｘ³−３ｘ²　の増減・極値を調べて、そのグラフを描いてみよう。

　　　ｙ’＝３ｘ²−６ｘ＝３ｘ（ｘ−２）＝０　より、　ｘ＝０、２

よって、増減表は、次の表のように なる。
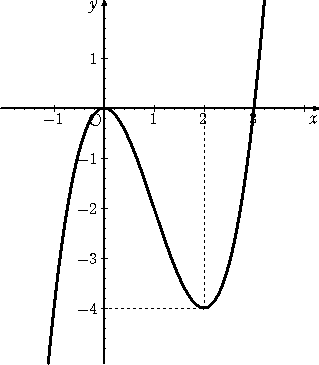したがって、求めるグラフは右図の実線 部分である。

　ここで、関数 ｙ の第２次導関数 ｙ” を考える。

　第１次導関数 ｙ’ の符号の変化で関数 ｙ の増減が分かるように、第２次導関数 ｙ” の符

号の変化で第１次導関数 ｙ’ の変化の様子を調べることができる。

　この場合、関数 ｙ’ の値は、関数 ｙ のグラフの接線の傾きであることに注意する。

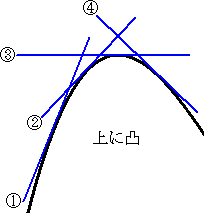
　　ｙ”＜０　となる ｘ の範囲で、関数 ｙ’ は単調に減少する。

このことを関数 ｙ の変化で考えると、 そのグラフは、上に凸 となる。

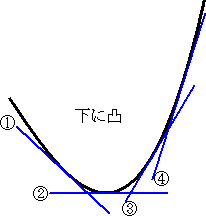
　　ｙ”＞０　となる ｘ の範囲で、関数 ｙ’ は単調に増加する。

このことを関数 ｙ の変化で考えると、 そのグラフは、下に凸 となる。

　関数 ｙ の凹凸が変化する点を、変曲点という。

　変曲点を求めるためには、

　　第２次導関数 ｙ” を求めて、 ｙ” ＝０　となる点における凹凸の変化を調べればよい。

例　３次関数 ｙ＝ｘ³−３ｘ²　の変曲点を求めてみよう。

　　ｙ’＝３ｘ²−６ｘ　より、　ｙ”＝６ｘ−６＝０　　　よって、　ｘ＝１

　ｘ＜１　のとき、　ｙ”＜０　より、　ｘ＜１　において、　関数 ｙ のグラフは、上に凸

　ｘ＞１　のとき、　ｙ”＞０　より、　ｘ＞１　において、　関数 ｙ のグラフは、下に凸

以上から、ｘ＝１　において、関数 ｙ の凹凸が変化するので、変曲点は、（１，−２）

例　４次関数 ｙ＝ｘ⁴　に変曲点はあるだろうか、調べてみよう。

　ｙ’＝４ｘ³　より、　ｙ”＝１２ｘ²＝０　　　よって、　ｘ＝０

　ｘ＜０　のとき、　ｙ”＞０　より、　ｘ＜０　において、　関数 ｙ のグラフは、下に凸

　ｘ＞０　のとき、　ｙ”＞０　より、　ｘ＞０　において、　関数 ｙ のグラフは、下に凸

以上から、ｘ＝０　において、関数 ｙ の凹凸が変化しないので、変曲点はない。

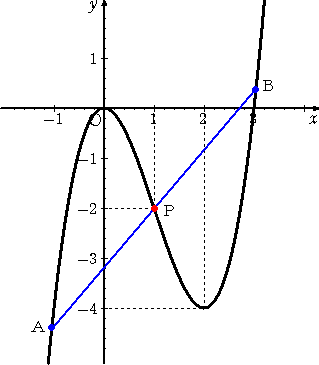
３次関数において、 　そのグラフは、変曲点に関して 対称である という大変美しい事実がある。 例　３次関数 ｙ＝ｘ3−３ｘ2　のグラフ 　　において、 　２点Ａ、Ｂは、変曲点Ｐに関して対称 の位置にある。

　この性質は、一般的には次のよう簡単に示すことができる。

　３次関数 Ｆ（ｘ）＝ａｘ³＋ｂｘ²＋ｃｘ＋ｄ　において、

　　Ｆ’（ｘ）＝３ａｘ²＋２ｂｘ＋ｃ　　より、　Ｆ”（ｘ）＝６ａｘ＋２ｂ＝０　を解いて、　ｘ＝−ｂ/(３ａ)

　このとき、関数 Ｆ（ｘ）のグラフを、ｘ 軸方向に　ｂ/(３ａ) 、ｙ 軸方向に　−Ｆ（−ｂ/(３ａ)）

だけ平行移動させると、

　Ｇ（ｘ）＝ａ（ｘ−ｂ/(３ａ)）³＋ｂ（ｘ−ｂ/(３ａ)）²＋ｃ（ｘ−ｂ/(３ａ)）＋ｄ−Ｆ（−ｂ/(３ａ)）

　　　　＝ａｘ³＋（ｃ−ｂ²/(３ａ)）ｘ

となる。

　よって、　Ｇ（−ｘ）＝−Ｇ（ｘ）　より、関数 Ｇ（ｘ）は奇関数となり、原点対称である。

したがって、３次関数 Ｆ（ｘ）は、変曲点Ｐ（−ｂ/(３ａ)、Ｆ（−ｂ/(３ａ)））に関して対称である。


　このことに関して、私の知人から次のような問題を考えたという話を伺った。

　３次関数において、変曲点が存在すれば、極大点・極小点は変曲点に関して対称
であることを示せ。

　この問題は、上記で証明した３次関数の性質を知っていれば自明であろう。そんなことを
知人に話したら、もっと別な解法があると言って、次のような解を示してくれた。

　Ｆ’（ｘ）＝ａ(ｘ−α)(ｘ−β)　とすると、関数 Ｆ（ｘ）は、　ｘ＝α、β　で極値を持つ。

また、　Ｆ”（ｘ）＝ａ(２ｘ−α−β)＝０　より、　ｘ＝（α＋β）/２　で関数 Ｆ（ｘ）は、変曲点となる。

　Ｆ’（ｘ）＝ａ｛(ｘ−α)²＋(α−β)(ｘ−α)｝　より、積分定数をＣとして、関数 Ｆ（ｘ）は、

　　　　　　Ｆ（ｘ）＝ａ｛(ｘ−α)³/３＋(α−β)(ｘ−α)²/２｝＋Ｃ

と書ける。このとき、

　　Ｆ（（α＋β）/２）＝ａ｛(（α＋β）/２−α)³/３＋(α−β)(（α＋β）/２−α)²/２｝＋Ｃ

　　　　　　　　　　　　＝ａ｛（β−α）³/２４＋(α−β)（β−α）²/８｝＋Ｃ

　　　　　　　　　　　　＝−ａ（β−α）³/１２＋Ｃ

また、　｛Ｆ（α）＋Ｆ（β）｝/２＝｛Ｃ＋ａ｛(β−α)³/３＋(α−β)(β−α)²/２｝＋Ｃ｝/２

　　　　　　　　　　　　　　　　　＝−ａ（β−α）³/１２＋Ｃ

なので、　　Ｆ（（α＋β）/２）＝｛Ｆ（α）＋Ｆ（β）｝/２　　が成り立つ。

　以上から、　極大点・極小点は変曲点に関して対称となる。

（コメント：　Ｆ’（ｘ）を、ｘ−αの降べきの順に整理する手法は、種々の問題に応用できる。）


変曲点の性質を用いた解法で一番感動する問題は次のようなものだろう。

問題　３次曲線 ｙ＝ｘ³−６ｘ²＋９ｘ と直線 ｙ＝ｋｘ が交わってできる２つの部分の面
　　　積が等しくなるように定数 ｋ の値を定めよ。

　　　　　

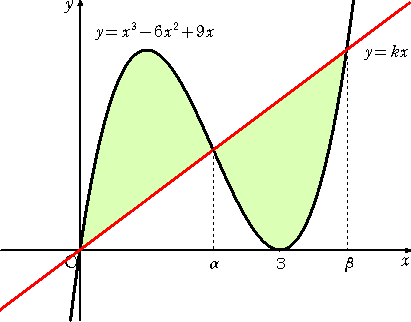
　この問題は、普通に積分計算しても求めることができるが、変曲点の性質を使えば積分
計算することなしに解かれる。

（解）　ｙ’＝３ｘ²−１２ｘ＋９　より、　ｙ”＝６ｘ−１２＝０　　　よって、　ｘ＝２

　　　ｘ＝２　において、関数 ｙ の凹凸が変化するので、変曲点は、（２，２）

　　３次曲線は変曲点に関して対称なので、直線 ｙ＝ｋｘ が変曲点を通るとき、２つの部分

　　の面積は等しくなる。

　　　よって、求める ｋ の値は、　ｋ＝１　である。

（コメント）　実際の受験で、このような解法をした場合、採点がどうなされるのか少し伺っ
　　　　　　てみたい気がする。

　上記の問題は、変曲点の性質を用いる一番有名なものであるが、次のような極値の問
題にも有効である。

（例）　関数 Ｆ(Ｘ) ＝ Ｘ³＋３Ｘ²−６Ｘ＋９　の極値の和を求めよ。

　　（解）　三次関数のグラフは、変曲点について点対称なので、変曲点は、極大点と極小

　　　　　点の中点である。

　　　　　　　Ｆ”(Ｘ) ＝６Ｘ＋６＝０　 より、Ｘ＝−１

　　　　　よって、Ｆ(−１)＝（極値の和）/２　なので、

　　　　　　　　　　　　（極値の和）＝２ Ｆ(−１)＝２×１７＝３４

　　　　である。（終）

　この問題は、通常次のように解かれていると思う。。

　　（解）　導関数　Ｆ’(Ｘ) ＝ ３Ｘ²＋６Ｘ−６ ＝ ３(Ｘ²＋２Ｘ−２) ＝ ０　は、相異なる２つの

　　　　　実数解　α 、 β （ α ＜ β ） を持ち、極大値は、Ｆ( α )、極小値は、Ｆ( β )で

　　　　　ある。　ここで、

　　　　　　　　　Ｘ³＋３Ｘ²−６Ｘ＋９ ＝ (Ｘ²＋２Ｘ−２)(Ｘ＋１)−６Ｘ＋１１

　　　　　なので、

　　　　　　　　（極値の和）＝ Ｆ( α )＋Ｆ( β ) ＝ (−６ α ＋１１)＋(−６ β ＋１１)

　　　　　　　　　　　　　　　＝ −６( α ＋ β )＋２２

　　　　　　　　　　　　　　　＝ ３４　　　（←　α ＋ β ＝−２　）　　（終）

（コメント）　２つの解を比較すると、変曲点の有用性に感動されることだろう。


　「変曲点に関して点対称」という性質ばかりに目がいくが、ちょっと視点の違う次のような
性質もあることを最近知ることができた。

例　３次関数 ｙ＝ｘ³−３ｘ²　は、上記で求めたように、

　　　　　　　　　

なので、ｘ＝０ で極大で極大値 ０ 、 ｘ＝２ で極小で極小値 −４ を持つ。

　このとき、２点（ ０ ， ０ ）、（ ２ ， −４ ）　を通る直線の傾きは、−２ である。

ところで、変曲点 （１，−２）における接線の傾きは、ｙ’＝３ｘ²−６ｘ＝−３　である。


　新しい性質を実証するために、もう一つ例をあげよう。

例　３次関数 ｙ＝ｘ³−３ｘ²−９ｘ＋１　において、

　　　　ｙ’＝３ｘ²−６ｘ−９＝３（ｘ²−２ｘ−３）＝３（ｘ−３)(ｘ＋１）＝０　より、　ｘ＝３、−１

　　よって、増減表は、次の表のようになる。

　　　　　　　　　

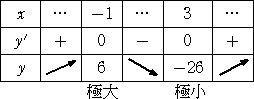
　　この関数について、上の例と同様な計算を行ってみよう。

　極大点（ −１ ， ６ ）、極小点（ ３ ， −２６ ）を通る直線の傾きは、

　　　　　　｛−２６−６｝/｛３−（−１）｝＝−８　 である。

ところで、ｙ”＝６ｘ−６＝０　より、変曲点は、 （１，−１０）　である。

　この変曲点における接線の傾きは、ｙ’＝３ｘ²−６ｘ−９＝−１２　である。

　上記の２つの例において、極点を結ぶ直線の傾きと変曲点における接線の傾きの関係

に注目すると、
　　　　　　　　　　　−２×（３/２）＝−３　　　−８×（３/２）＝−１２

がともに成り立つことから、次の性質の成り立つことが推察される。

　　（変曲点における接線の傾き）＝（極点を結ぶ直線の傾き）×（３/２）

　この性質は、次のようにして簡単に示される。

（証明）　Ｆ’（ｘ）＝ａ(ｘ−α)(ｘ−β)　とすると、関数 Ｆ（ｘ）は、　ｘ＝α、β　で極値を持つ。

また、　Ｆ”（ｘ）＝ａ(２ｘ−α−β)＝０　より、　ｘ＝（α＋β）/２　で関数 Ｆ（ｘ）は、変曲点となる。

このとき、変曲点における接線の傾きは、

　Ｆ’（（α＋β）/２）＝ａ(（α＋β）/２−α)(（α＋β）/２−β)＝−ａ（β−α）²/４

また、　Ｆ’（ｘ）＝ａ｛(ｘ−α)²＋(α−β)(ｘ−α)｝　より、積分定数をＣとして、関数 Ｆ（ｘ）は、

　　　　　　Ｆ（ｘ）＝ａ｛(ｘ−α)³/３＋(α−β)(ｘ−α)²/２｝＋Ｃ

と書ける。このとき、極点を結ぶ直線の傾きは、

｛　Ｆ（β）−Ｆ（α）｝/（β−α）＝ａ｛(β−α)³/３＋(α−β)(β−α)²/２｝/（β−α）

　　　　　　　　　　　　　　　　　　　＝−ａ（β−α）²/６

したがって、　｛　Ｆ（β）−Ｆ（α）｝/（β−α）×（３/２）＝−ａ（β−α）²/４＝Ｆ’（（α＋β）/２）

よって、　　（極点を結ぶ直線の傾き）×（３/２）＝（変曲点における接線の傾き）

が成り立つ。（証終）

　今証明した性質は、次のような問題を解くときに有効であろう。（ある意味で、裏技！）

問題　３次関数 Ｆ（ｘ）＝ａｘ³＋ｂｘ²＋ｃｘ＋ｄ　で、ｘ＝ −１ のとき極大値が ６ 、
　　　ｘ＝ ３ のとき極小値が −２６ であるものを求めよ。

（解）　求める３次関数の導関数は、 Ｆ’（ｘ）＝ｋ(ｘ＋１)(ｘ−３)＝ｋ(ｘ²−２ｘ−３)　　（ｋ＞０）

　　とおける。　このとき、

　　　　　　Ｆ”（ｘ）＝２ｋ（ｘ−１）＝０　より、　ｘ＝１　なので、　　Ｆ’（１）＝−４ｋ

　　ここで、極点を結ぶ直線の傾きは、｛−２６−６｝/｛３−（−１）｝＝−８　なので、

　　変曲点の性質から、　　−４ｋ＝（−８）×（３/２）＝−１２　より、　ｋ＝３　となる。

よって、　Ｆ’（ｘ）＝３(ｘ²−２ｘ−３)＝３ｘ²−６ｘ−９　となり、

　　　Ｆ（ｘ）＝ｘ³−３ｘ²−９ｘ＋ｄ　　（ｄ は積分定数）

ここで、　Ｆ（−１）＝６　より、　−１−３＋９＋ｄ＝６　　よって、　ｄ＝１

　したがって、　　Ｆ（ｘ）＝ｘ³−３ｘ²−９ｘ＋１　　（終）


　これに対して、教科書等では通常次のように解かれる。

（別解）　Ｆ’（ｘ）＝３ａｘ²＋２ｂｘ＋ｃ　において、　Ｆ’（−１）＝０　、Ｆ’（３）＝０　だから、
　　　　　　３ａ−２ｂ＋ｃ ＝ ０　　・・・　（１）　　　　　２７ａ＋６ｂ＋ｃ ＝ ０　　・・・　（２）

　　　また、　Ｆ（−１）＝６　、Ｆ（３）＝−２６　なので、
　　　　　−ａ＋ｂ−ｃ＋ｄ ＝ ６　　・・・　（３）　　　２７ａ＋９ｂ＋３ｃ＋ｄ ＝ −２６　　・・・　（４）

　（４）−（３）より、　２８ａ＋８ｂ＋４ｃ ＝ −３２　　よって、　７ａ＋２ｂ＋ｃ ＝ −８　　・・・　（５）

　（５）−（１）より、　４ａ＋４ｂ ＝ −８　　　よって、　ａ＋ｂ ＝ −２　　・・・　（６）
　（２）−（５）より、　２０ａ＋４ｂ ＝ ８　　　よって、　５ａ＋ｂ ＝ ２　　・・・　（７）

よって、　（７）−（６）より、　４ａ＝４　　　　よって、　ａ ＝ １

このとき、　ｂ ＝ −３　　で、また、　ｃ ＝ −９　　、　ｄ ＝ １　なので、

　　　　　Ｆ（ｘ）＝ｘ³−３ｘ²−９ｘ＋１

この関数 Ｆ（ｘ） は条件を満たす。　（終）

（コメント）　上記２つの解を比較すると文字の個数が少ない分、変曲点の性質を使った解
　　　　　　の方がスッキリしている。（別解）の方は、あまりやりたくない計算だ！


（追記）　平成１８年１２月１３日付け

　３次関数のグラフが描けても、グラフそのものの持つ美しい性質に目を向ける生徒は少
ない。変曲点に関する対称性は有名な事実であるが、それ以外にも３次関数には魅力的
な性質が隠れている。

　例えば、 ３次関数 Ｆ（ｘ）＝ｘ³−３ｘ²　の増減・極値を調べて、そのグラフを描いてみると、

　　

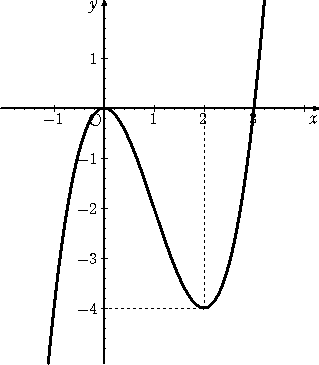
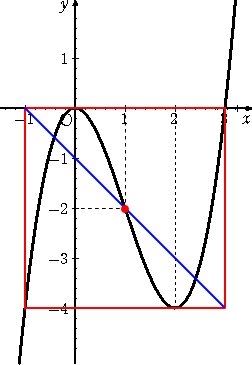
となる。（左図）　ここで、　極大値が ０ で、　Ｆ（ｘ）＝０　となる ｘ の値は、　ｘ＝０ 、３

　また、極小値が −４ で、　Ｆ（ｘ）＝−４　となる ｘ の値は、　ｘ³−３ｘ²＝−４　より、

　　ｘ³−３ｘ²＋４＝０　　すなわち、　（ｘ−２）²（ｘ＋１）＝０　　よって、　ｘ＝２ 、−１

　このとき、右図のような長方形（赤色部分）が得られ、変曲点は丁度長方形の対角線上
にある。

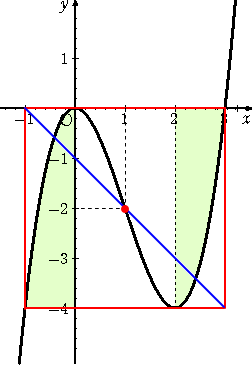このことは、３次関数のグラフの一般的な性質 　　なのだろうか？あるいは、たまたま上記の関数 　　においてのみ成り立つ性質なのだろうか？ 　　　変曲点の性質から、やはり、このことは一般的 　　に成り立つ事実である。 　　　左図を、じっと睨めっこをすれば、上述のことが 　　一般的性質であることが了解できるだろう。

　代数的にも成り立つことを確認しておこう。

　３次関数 Ｆ（ｘ）＝ａｘ³＋ｂｘ²＋ｃｘ＋ｄ　において、 ｘ＝α で極大、 ｘ＝β で極小　（α＜β）

とする。　このとき、　変曲点の ｘ 座標は、　（α＋β）/２　である。

　いま、極大値が Ｆ（α） で、　Ｆ（ｘ）＝Ｆ（α）　となる ｘ の値を求める。

　　Ｆ（ｘ）−Ｆ（α）＝ａ（ｘ−α）²（ｘ−γ）　　（ａ＞０）　とおく。

両辺を２回微分して、　Ｆ”（ｘ）＝２ａ（３ｘ−２α−γ）

　　Ｆ”（（α＋β）/２）＝０　なので、　　（３（α＋β）/２−２α−γ）＝０

　よって、　γ＝（３β−α）/２　でなければならない。

　　ここで、　（γ＋（α＋β）/２）/２＝β　という事実から、変曲点より得られる

点（ （α＋β）/２ ， ０ ）と点（ γ ， ０ ）の中点が丁度、点（ β ， ０ ）になっている。

　同様にして、極小値が Ｆ（β） で、　Ｆ（ｘ）＝Ｆ（β）　となる ｘ の値を求める。

　　Ｆ（ｘ）−Ｆ（β）＝ａ（ｘ−β）²（ｘ−δ）　　（ａ＞０）　とおく。

　両辺を２回微分して、　Ｆ”（ｘ）＝２ａ（３ｘ−２β−δ）

　　Ｆ”（（α＋β）/２）＝０　なので、　　（３（α＋β）/２−２β−δ）＝０

　よって、　δ＝（３α−β）/２　でなければならない。

　　ここで、　（δ＋（α＋β）/２）/２＝α　という事実から、変曲点より得られる

点（ （α＋β）/２ ， ０ ）と点（ δ ， ０ ）の中点が丁度、点（ α ， ０ ）になっている。


　上記の計算から、極値をもつ、どんな３次関数であれ、そのグラフは、均整の取れた長
方形の中で、美しさを発露させていることが分かる。（下図参照）

　　　　　　　　　



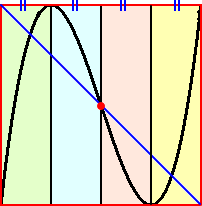
　　　　以下、工事中