角柱（円柱を含む）や角錐（円錐を含む）の体積の公式は、皆さんにとって周知のものだろう。
当ＨＰでも
四面体の求積 三角錐の体積 円柱の体積 直交する円柱 角錐の体積
ある図形の体積 切断面の高さ ・・・
などが話題となり、まとめられてきた。このページでは、立体図形の体積について、さらなる
考察を試みたいと思う。
例題 上面、下面が平行（各面の長方形の辺どうしが平行）な四角錐台の体積を求めよ。
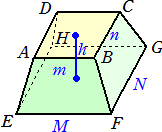
体積は、 ｈ(２ＭＮ＋Ｍｎ＋ｍＮ＋２ｍｎ)/６ で与えられる。
特に、ｍ＝ｎ＝０ とすれば、四角錐の体積 ｈＭＮ/６ となる。
Ｍ＝ｍ、Ｎ＝ｎ とすれば、直方体の体積 ｈＭＮ となる。
（解） 立体図形は、長方形ＥＦＧＨを底面とする四角錐Ｏ-ＥＦＧＨから長方形ＡＢＣＤを底面
とする四角錐Ｏ-ＡＢＣＤを取り除いたものである。
ＯＡ ： ＯＥ＝１ ： ｋ とすると、 Ｍ＝ｋｍ 、Ｎ＝ｋｎ が成り立つ。
また、四角錐Ｏ-ＡＢＣＤの高さを ｘ とおくと、 ｘ ： ｘ＋ｈ＝１ ： ｋ なので、 ｘ＝ｈ/（ｋ－１）
このとき、 ｘ＋ｈ＝ｈｋ/（ｋ－１） である。
よって、 四角錐Ｏ-ＡＢＣＤの体積Ｖ1は、 Ｖ1＝ｍｎｈ/｛３（ｋ－１）｝
四角錐Ｏ-ＥＦＧＨの体積Ｖ2は、 Ｖ2＝ＭＮｈｋ/｛３（ｋ－１）｝＝ｍｎｈｋ3/｛３（ｋ－１）｝
したがって、求める立体図形の体積は、
Ｖ2－Ｖ1＝ｍｎｈｋ3/｛３（ｋ－１）｝－ｍｎｈ/｛３（ｋ－１）｝
＝ｍｎｈ（ｋ3－１）/｛３（ｋ－１）｝
＝ｍｎｈ（ｋ2＋ｋ＋１）/３
＝ｈ（ｍｋ・ｎｋ＋ｍｎｋ＋ｍｎ）/３
＝ｈ（２ｍｋ・ｎｋ＋ｍｎｋ＋ｍｎｋ＋２ｍｎ）/６
＝ｈ（２ＭＮ＋Ｍｎ＋ｍＮ＋２ｍｎ）/６ （終）
（別解） 立体図形を下図のように３つの部分に分割する。
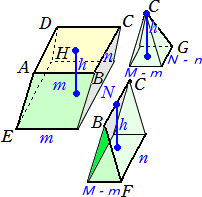
このとき、求める立体図形の体積は、
（Ｎ＋ｎ）ｈｍ/２＋（Ｍ－ｍ）ｈｎ/２＋（Ｍ－ｍ）（Ｎ－ｎ）ｈ/３
＝ｈ（３Ｎｍ＋３ｍｎ＋３Ｍｎ－３ｍｎ＋２ＭＮ－２Ｍｎ－２Ｎｍ＋２ｍｎ）/６
＝ｈ（２ＭＮ＋Ｍｎ＋Ｎｍ＋２ｍｎ）/６ （終）
（追記） 令和４年７月２７日付け
次の立体図形の体積を求める方法としては、いろいろ考えられる。
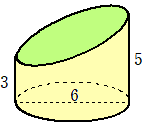
最初に思いついたのが、下図のように斜めになってる部分をならす方法である。
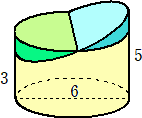
このとき、求める体積は、直径６の円を底面とし高さが （３＋５）/２＝４ の円柱の体積に
等しくなるので、
体積＝９π×４＝３６π
となる。また、同じ図形をもう１個用意して、下図のように逆向きに重ねる方法も有効である。
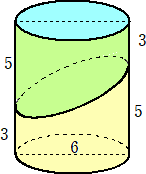
このとき、求める体積は、直径６の円を底面とし高さが８の円柱の体積の半分に等しくな
るので、
体積＝９π×８÷２＝３６π
となる。
この後半の手法は、是非覚えておきたいテクニックである。
（追記） 令和４年７月２８日付け
問題 １辺の長さが６の立方体ＡＢＣＤ-ＥＦＧＨがある。辺ＣＤを２：１に内分する点をＰ、辺
ＧＨを１：２に内分する点をＱとする。今、立方体を３点Ａ、Ｐ、Ｑを通る平面αで切断
したとき、次の問いに答えよ。
（１） 平面αと辺ＥＦの交点をＲとおくとき、線分ＥＲの長さを求めよ。
（２） 立体ＡＰＤ－ＥＲＱＨの体積を求めよ。
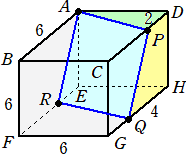
（解）（１） Ｒより辺ＧＨに垂線を下ろし、その足をＳとすると、 △ＡＰＤ≡△ＲＱＳ
ＱＳ＝ＰＤ＝２ なので、 ＥＲ＝４－２＝２
（２） 立体ＡＰＤ－ＥＲＱＨをもう一つ考え、下図のように合体させる。
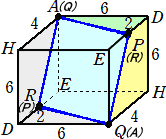
このとき、求める体積は、上図の直方体の体積の半分なので、
６×４×６÷２＝７２ （終）
（追記） 令和４年７月３０日付け
次の女子学院中学の入試問題（２００９）は、目新しい立体図形の体積の計算である。慣
れていないと大変かもしれない。問題は若干改題してあります。
問題 ４つの直方体を組み合わせて、下図のような立体を作る。
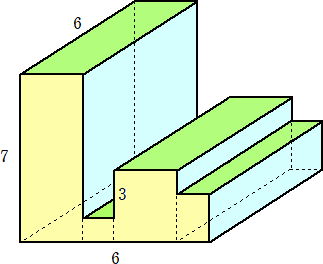
この立体図形の表面積が２４６のとき、体積を求めよ。
（解） 立体図形の上下の面の面積は、 ６×６×２＝７２
立体図形の左右の面の面積は、 ７×６×２＝８４
上記の左右の面の面積計算でもれている部分の面積は、 ３×６×２＝３６
よって、立体図形の表面積は、
（立体図形の前後の面積）＋７２＋８４＋３６＝２４６
これより、 （立体図形の前後の面積）＝５４ なので、求める立体図形の体積は、
５４÷２×６＝１６２ （終）
（追記） 令和４年８月１９日付け
体積計算では、いくつかの基本図形に分割して考えることが基本である。
問題 下図の直方体ＡＢＣＤ-ＥＦＧＨにおいて、ＰはＡＢを１：２に分ける点、ＱはＣＤを１：２
に分ける点、ＲはＦＧの中点、ＳはＨＥの中点である。
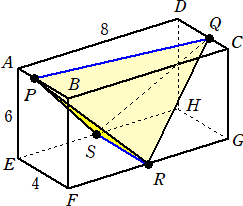
（解） ４×６÷２×８÷３＝３２ （終）
問題 下図のような三角柱ＡＢＣ－ＤＥＦにおいて、辺ＣＦ上にＣＰ＝ｐ となる点Ｐをとる。
三角錐Ｐ－ＡＢＣの体積が三角柱ＡＢＣ－ＤＥＦの体積の１/９であるとき、ｐ の値を求めよ。
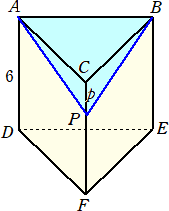
（解） ６×△ＡＢＣ×１/９＝ｐ×△ＡＢＣ×１/３ より、 ｐ＝２ （終）
以下、工事中！