
丂摉俫俹偺撉幰偺俲丏俽丏偝傫傛傝丄暯惉俀係擭侾侽寧侾侽擔晅偗偱昗婰榖戣傪儊乕儖偱捀偄偨丅
丂尨揰傪俷偲偟丄嬻娫忋偺俁揰俙乮倎1丆倎2丆倎3乯丄俛乮倐1丆倐2丆倐3乯丄俠乮們1丆們2丆們3乯偲偡傞丅
丂偙偺偲偒丄嶰妏悕 俷-俙俛俠 偺懱愊倁偼丄師幃偱梌偊傜傟傞丅
丂丂丂
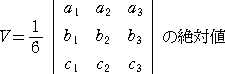
乮徹柧侾乯丂俁揰俙乮倎1丆倎2丆倎3乯丄俛乮倐1丆倐2丆倐3乯丄俠乮們1丆們2丆們3乯傪捠傞暯柺偺曽掱幃傪
丂丂丂丂丂倎倶亄倐倷亄們倸亖侾丂偲偡傞偲丄尨揰俷偐傜暯柺傊偺嫍棧 倛 偼丄
丂丂丂丂丂丂
丂丂丂丂傑偨丄仮俙俛俠偺柺愊 俽 偼丄丂俽亖乮侾/俀乯乥俙俛亊俙俠乥
丂丂丂丂丂傛偭偰丄丂倁亖乮侾/俁乯俽倛丂偐傜丄
丂丂丂丂丂丂丂
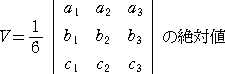 丂丂丂乮徹廔乯
丂丂丂乮徹廔乯乮徹柧俀乯丂倶丄倷丄倸幉偵懳偡傞夞揮峴楍偵傛傝丄揰俙丄俛偑暯柺 倸亖侽 忋偵偺傞傛偆偵偡傞偙
丂丂丂丂丂偲偑偱偒傞丅夞揮峴楍偺峴楍幃偺抣偼侾側偺偱丄懱愊傕曄壔偟側偄丅嬶懱揑偵偼丄
丂丂丂丂丂揰俙偑暯柺 倷亖侽 忋偵偁傞傛偆偵倸幉夞揮偟丄偝傜偵丄倷幉夞揮偵傛傝丄揰俙傪倶幉忋
丂丂丂丂丂偵堏摦偝偣傞丅師偵丄揰俛傪倶幉夞揮偵傛傝丄暯柺倸亖侽忋偵堏偡丅丂丂乮徹廔乯
乮僐儊儞僩乯丂乮徹柧俀乯偺曽朄偼丄峴楍幃偺娙棯壔傪峫偊傟偽偄偄偺偩傠偆丏丏丏丅
乮捛婰乯丂暯惉俀俇擭侾寧俀侾擔晅偗
丂侾曈係偺棫曽懱俙俛俠俢-俤俥俧俫偑偁傞丅俛俠忋偵俛俹亖侾丄俤俥忋偵俥俻亖侾丄俧俫忋偵俫俼亖俀
偲側傞揰俹丄俻丄俼傪偲傞丅
丂偙偺偲偒丄巐柺懱俙俹俻俼偺懱愊傪媮傔傛丅
乮嶲峫丗拀攇戝妛晬懏嬵応崅峑悢妛壢妛尋媶夛曇丂乽俠倎倖倕丂俛倧倢倢倵倕們倠丂俶倧丏嘮乿乯
乮夝乯丂俙乮侽丆侽丆侽乯丄俛乮係丆侽丆侽乯丄俢乮侽丆係丆侽乯丄俤乮侽丆侽丆係乯偲偍偔偲丄
丂丂丂丂丂俹乮係丆侾丆侽乯丄俻乮俁丆侽丆係乯丄俼乮俀丆係丆係乯
丂丂傛偭偰丄俙俹亖乮係丆侾丆侽乯丄俙俻亖乮俁丆侽丆係乯丄俙俼亖乮俀丆係丆係乯丂偑掕傔傞嶰妏悕偺懱愊
丂偼丄忋婰偺岞幃偵戙擖偟偰丄俁係/俁偲側傞丅丂丂乮廔乯
丂乽俠倎倖倕丂俛倧倢倢倵倕們倠丂俶倧丏嘮乿偵傛傟偽丄師偺傛偆偵婔壗揑偵夝偗傞偲偺偙偲丅慺惏傜偟偄両
乮暿夝乯丂俥俧忋偵俥俽亖侾偲側傞俽傪偲傝丄俤俽偲俻俼偺岎揰傪俿偲偡傞丅偡傞偲丄柺俙俤俽俹偲俻俼
丂丂丂丂偼悅捈偵岎傢傞偺偱丄巐柺懱俙俹俻俼偺懱愊偼丄
丂丂丂仮俙俹俿丒俻俼/俁亖乮俙俹丒俙俤/俀乯丒俻俼/俁亖乮俤俽丒係/俀乯丒俻俼/俁
丂丂丂丂丂丂丂丂丂丂丂丂亖俤俽丒俻俼丒俀/俁亖俤俽2丒俀/俁亖侾俈丒俀/俁亖俁係/俁丂丂乮廔乯
乮捛婰乯丂椷榓係擭侾侽寧俀俋擔晅偗
丂杒奀摴戝妛丂慜婜棟宯乮俀侽侽俋乯偱丄嶰妏悕偺揥奐恾偐傜尦偺棫懱恾宍偺懱愊傪媮傔偝
偣傞栤戣偑弌戣偝傟偨丅
侾丏壓恾偼丄偁傞嶰妏悕偺揥奐恾偱偁傞丅偙偙偱丄俙俛亖係丄俙俠亖俁丄俛俠亖俆丄佢俙俠俢亖俋侽亱
丂偱丄仮俙俛俤偼惓嶰妏宍偱偁傞丅偙偺偲偒丄嶰妏悕偺懱愊傪媮傔傛丅
丂丂丂丂丂
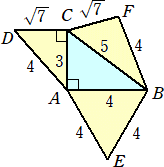
乮夝乯丂俙乮侽丆侽丆侽乯丄俛乮係丆侽丆侽乯丄俠乮侽丆俁丆侽乯偲偍偒丄嶰妏悕偺捀揰傪俹乮倶丆倷丆倸乯偲偍偔丅
丂懱愊偺寁嶼側偺偱丄丂倸亜侽丂偲偟偰傛偄丅
丂戣堄傛傝丄丂俹俙亖俹俛亖係丂丄俹俠亖
丂倶2亄倷2亄倸2亖侾俇丂丒丒丒丂乮侾乯
丂乮倶亅係乯2亄倷2亄倸2亖侾俇丂丒丒丒丂乮俀乯
丂倶2亄乮倷亅俁乯2亄倸2亖俈丂丒丒丒丂乮俁乯
乮侾乯亅乮俀乯傛傝丄丂俉倶亅侾俇亖侽丂側偺偱丄丂倶亖俀
乮侾乯亅乮俁乯傛傝丄丂俇倷亅俋亖俋丂側偺偱丄丂倷亖俁
乮侾乯偵戙擖偟偰丄丂係亄俋亄倸2亖侾俇丂傛傝丄丂倸亖
丂傛偭偰丄媮傔傞懱愊偼丄丂俇亊
丂丂埲壓丄岺帠拞両