
丂侾曈偺挿偝偑 倎 偺惓巐柺懱 俷俙俛俠 偺懱愊 倁 偼丄傛偔抦傜傟偰偄傞傛偆偵丄
丂丂丂丂丂丂丂丂
偱梌偊傜傟傞丅
丂堦墳丄徹柧偟偰偍偙偆丅
乮徹柧乯丂掙柺偺惓嶰妏宍俙俛俠偺柺愊偼丄丂乮侾/俀乯倎2丒乮
丂仮俙俛俠偺廳怱傪俧偲偍偔偲丄惓巐柺懱偺崅偝偼丄俷俧偱梌偊傜傟傞丅
丂偙偙偱丄丂俙俧亖乮
丂丂俷俧2亖倎2亅乮侾/俁乯倎2亖乮俀/俁乯倎2丂側偺偱丄丂俷俧亖乮
丂埲忋偐傜丄惓巐柺懱 俷俙俛俠 偺懱愊 倁 偼丄
丂丂倁亖乮
丂崱傑偱忋婰偺徹柧偱枮懌偟偰偄偨偑丄師偺傛偆側暿徹偑偁傞偙偲傪嵟嬤抦傞偙偲偑弌棃偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮椷榓俁擭俁寧俀俉擔晅偗乯
乮暿徹乯丂曈俷俠偺拞揰傪俵偲偍偔偲丄曈俷俠佦暯柺俵俙俛丂偱偁傞丅
丂俵俙亖俵俛亖乮
丂偙偺偲偒丄丂俵俶2亖乮俁/係乯倎2亅乮侾/係乯倎2亖乮侾/俀乯倎2丂傛傝丄丂俵俶亖乮
丂埲忋偐傜丄惓巐柺懱 俷俙俛俠 偺懱愊 倁 偼丄
丂丂倁亖倎亊乮
丂傑偨丄侾師撈棫側俁偮偺儀僋僩儖 俷俙 丄俷俛 丄俷俠 偵傛傝丄
丂丂丂丂丂丂丂丂倁亖乥乮 俷俙 丆俷俛亊俷俠 乯/俇 乥
偱梌偊傜傟傞偙偲傕桳柤偩傠偆丅丂乮丂丆丂乯偼撪愊偱偁傝丄亊偼奜愊偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮仺丂嶲峫丗乽悅捈傪媮傔傞乿乯
丂偙偺儁乕僕偱偼丄堦斒偺巐柺懱偵偮偄偰丄偄傠偄傠側彅忦審偐傜丄偦偺懱愊傪媮傔傞曽
朄偵偮偄偰丄傑偲傔傛偆偲巚偆丅
丂丂丂丂丂丂丂丂丂丂丂丂
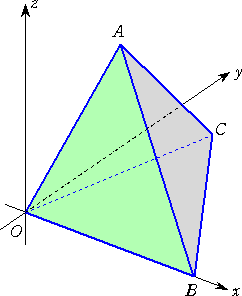
乮侾乯丂巐柺懱 俷俙俛俠 偺奺捀揰偺嵗昗偑梌偊傜傟傞応崌
丂丂丂俷乮 侽 丆 侽 丆 侽 乯 丄 俙乮 倶1 丆 倷1 丆 倸1 乯 丄 俛乮 倶2 丆 倷2 丆 倸2 乯丄俠乮 倶3 丆 倷3 丆 倸3 乯
丂丂傪係捀揰偲偡傞巐柺懱 俷俙俛俠 偺懱愊 倁 偼丄
丂丂丂丂丂丂丂丂
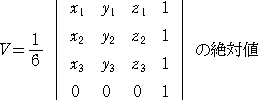
丂丂偱梌偊傜傟傞丅
乮徹柧乯丂俷俙亖乮 倶1 丆 倷1 丆 倸1 乯丂丄俷俛亖乮 倶2 丆 倷2 丆 倸2 乯丂丄俷俠亖乮 倶3 丆 倷3 丆 倸3 乯
丂丂丂丂偵偍偄偰丄丂俷俛亊俷俠亖乮 倷2倸3亅倷3倸2 丆 倸2倶3亅倸3倶2 丆 倶2倷3亅倶3倷2 乯丂偱偁傞丅
丂丂丂丂丂偲偙傠偱丄峴楍幃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
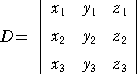
丂丂丂丂丂偵偍偄偰丄俷俛亊俷俠 偺 倶 嵗昗 倷2倸3亅倷3倸2 偼丄俢 偺 倶1 偵娭偡傞梋場巕
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂偱偁傝丄俷俛亊俷俠 偺 倷 嵗昗 倸2倶3亅倸3倶2 偼丄俢 偺 倷1 偵娭偡傞梋場巕
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂偱偁傝丄俷俛亊俷俠 偺 倸 嵗昗 倶2倷3亅倶3倷2 偼丄俢 偺 倸1 偵娭偡傞梋場巕
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂偱偁傞丅
丂丂丂丂丂丂廬偭偰丄丂乮 俷俙 丆俷俛亊俷俠 乯亖倶1倃1 亄 倷1倄1 亄 倸1倅1亖俢丂偱偁傞丅
丂丂丂丂丂偙偺偙偲偐傜丄梌幃偑惉傝棫偮偙偲偼柧傜偐偩傠偆丅丂乮徹廔乯
乮俀乯丂巐柺懱 俷俙俛俠 偺奺曈偺挿偝偑梌偊傜傟傞応崌
丂丂丂俷俙 亖 倎 丄 俷俛 亖 倐 丄 俷俠 亖 們 丄 俙俛 亖 倫 丄 俙俠 亖 倯 丄 俛俠 亖 倰丂偲偡傞丅
丂丂丂偙偺偲偒丄巐柺懱 俷俙俛俠 偺懱愊 倁 偼丄
丂丂丂丂丂丂丂丂

丂丂偱梌偊傜傟傞丅
乮徹柧乯丂忦審傛傝丄丂倎 亖乥俷俙乥 丄 倐 亖乥俷俛乥 丄 們 亖乥俷俠乥丂偱偁傞丅
丂丂丂傑偨丄丂倫2亖乥俙俛乥2亖乥俷俛乥2亅俀乮俷俙 丆俷俛乯亄乥俷俙乥2丂傛傝丄
丂丂丂丂丂丂丂丂丂丂乮俷俙 丆俷俛乯亖乮倎2亄倐2亅倫2乯/俀
丂丂丂偲側傞丅摨條偵偟偰丄
丂丂丂丂乮俷俙 丆俷俠乯亖乮倎2亄們2亅倯2乯/俀丂丂丄乮俷俛 丆俷俠乯亖乮倐2亄們2亅倰2乯/俀
丂丂丂丂偄傑丄丂俷俙亖乮 倶1 丆 倷1 丆 倸1 乯丂丄俷俛亖乮 倶2 丆 倷2 丆 倸2 乯丂丄俷俠亖乮 倶3 丆 倷3 丆 倸3 乯
丂丂丂偲偡傞偲丄
丂丂丂丂丂丂丂丂
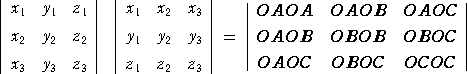
丂丂丂側偺偱丄
丂丂丂丂丂丂
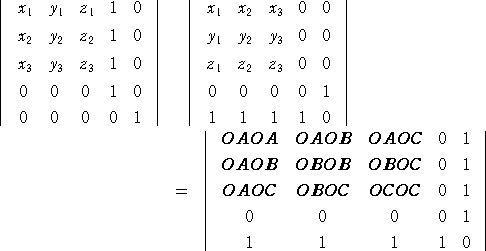
丂丂丂偑惉傝棫偮丅丂柧傜偐偵丄嵍曈偼丄丂亅乮俇倁乯2亖亅俁俇倁2丂偵摍偟偄丅
丂丂丂塃曈偼丄
丂丂丂丂丂丂丂丂丂丂
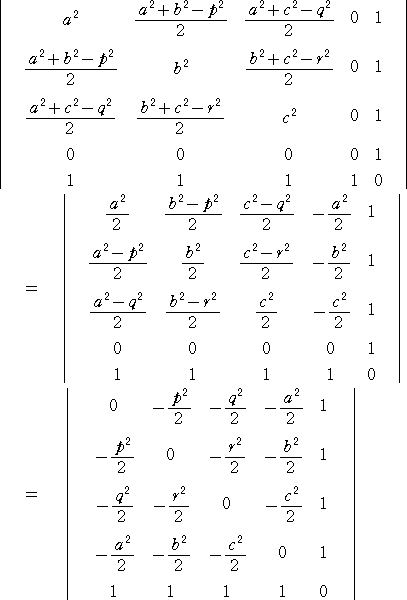
丂丂丂丂偲側傝丄
丂丂丂丂丂丂丂丂丂
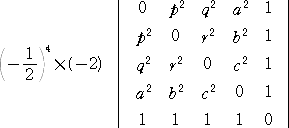
丂丂丂丂偐傜丄梌幃偺惉傝棫偮偙偲偼柧傜偐偩傠偆丅丂乮徹廔乯
乮僐儊儞僩乯丂惓巐柺懱 俷俙俛俠 偺懱愊 倁 傪丄偙偺岞幃傪梡偄偰媮傔傞偙偲偼丄偁傑傝尗柧側
丂丂丂丂丂丂曽朄偲偼尵偊側偄丅幚嵺偵寁嶼偟偰傒偰戝曄偩偭偨傕偺偱丏丏丏丅
乮俁乯丂巐柺懱 俷俙俛俠 偺奺柺偺曽掱幃偑梌偊傜傟傞応崌
丂丂丂仮俷俙俛丄仮俷俛俠丄仮俷俠俙丄仮俙俛俠丂偺奺柺偺曽掱幃傪丄
丂丂丂丂丂丂丂丂倎1倶亄倐1倷亄們1倸亄倓1亖侽
丂丂丂丂丂丂丂丂倎2倶亄倐2倷亄們2倸亄倓2亖侽
丂丂丂丂丂丂丂丂倎3倶亄倐3倷亄們3倸亄倓3亖侽
丂丂丂丂丂丂丂丂倎4倶亄倐4倷亄們4倸亄倓4亖侽
丂丂丂偲偡傞丅丂峴楍幃
丂丂丂丂丂丂丂丂丂

丂丂丂偺丄奺 倓倠 乮倠亖侾丆俀丆俁丆係乯偵娭偡傞梋場巕傪丄俢倠 偲偍偔丅
丂丂丂丂偙偺偲偒丄巐柺懱 俷俙俛俠 偺懱愊 倁 偼丄
丂丂丂丂丂丂丂丂丂
丂丂丂偱梌偊傜傟傞丅
乮徹柧乯丂峴楍幃 俢 偺 奺 倎倠 丄倐倠 丄們倠 乮倠亖侾丆俀丆俁丆係乯偵娭偡傞梋場巕傪丄偦傟偧傟
丂丂丂丂俙倠 丄俛倠 丄俠倠丂偲偍偔丅
丂丂丂楢棫堦師曽掱幃偵偍偗傞僋儔乕儊儖偺岞幃偐傜丄巐柺懱 俷俙俛俠 偺係捀揰偺嵗昗偼丄
丂丂丂丂丂俷乮 俙4/俢4 丆 俛4/俢4 丆 俠4/俢4 乯 丄 俙乮 俙2/俢2 丆 俛2/俢2 丆 俠2/俢2 乯 丄
丂丂丂丂丂俛乮 俙3/俢3 丆 俛3/俢3 丆 俠3/俢3 乯 丄 俠乮 俙1/俢1 丆 俛1/俢1 丆 俠1/俢1 乯
丂丂偲側傞丅丂偟偨偑偭偰丄
丂丂丂丂丂丂丂丂
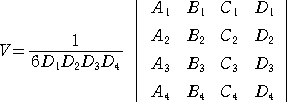
丂丂丂偲偙傠偱丄
丂丂丂丂丂丂丂丂丂丂
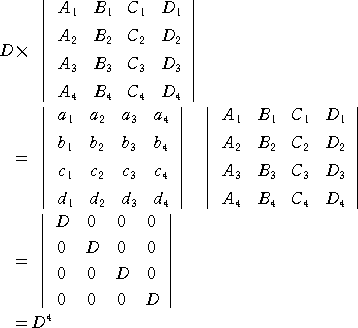
丂丂丂側偺偱丄梌幃偺惉傝棫偮偙偲偼柧傜偐偩傠偆丅丂乮徹廔乯
乮捛婰乯丂暯惉俀侽擭俋寧侾侽擔晅偗
丂嵟嬤丄師偺傛偆側巐柺懱偺懱愊傪媮傔傞婡夛偑偁偭偨丅
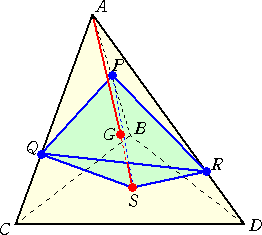 丂丂懱愊偑俆偺巐柺懱俙俛俠俢偵偍偄偰丄曈俙俛
丂丂懱愊偑俆偺巐柺懱俙俛俠俢偵偍偄偰丄曈俙俛丂偺拞揰傪俹丄曈俙俠傪 俀 丗 侾 偵撪暘偡傞揰傪
丂俻丄曈俙俢傪 俁 丗 侾 偵撪暘偡傞揰傪俼偲偡傞丅
丂丂仮俹俻俼偺廳怱俧偲捀揰俙傪捠傞捈慄偑掙
丂柺俛俠俢偲岎傢傞揰傪俽偲偡傞丅
丂丂偙偺偲偒丄巐柺懱俹俻俼俽偺懱愊傪媮傔傛丅
丂偙偺栤戣偼嬻娫攃埇偵庛偄尰栶偺庴尡惗偵偲偭偰椙栤偺晹椶偵擖傞栤戣偲尵偊傞丅
丂慄暘偺斾偺寁嶼偵偼丄儀僋僩儖偺奣擮乮偟偨偑偭偰丄悢妛俛偺斖醗両乯偑梡偄傜傟傞偑丄
幚嵺偺懱愊偺寁嶼偺杮幙揑側晹暘偼悢妛嘥偺斖醗偱偁傞丅
乮夝乯丂俙俹亖乮1/2乯俙俛丂丄俙俻亖乮2/3乯俙俠丂丄俙俼亖乮3/4乯俙俢丂側偺偱丄
丂丂丂俙俧亖乮俙俹亄俙俻亄俙俼乯/俁亖乮1/6乯俙俛亄乮2/9乯俙俠亄乮1/4乯俙俢
丂丂俙俽亖倠俙俧亖倠乷乮1/6乯俙俛亄乮2/9乯俙俠亄乮1/4乯俙俢乸丂偵偍偄偰丄
丂丂揰俽偼暯柺俛俠俢忋偺揰偱偁傞偺偱丄
丂丂丂丂丂丂倠乷乮1/6乯亄乮2/9乯亄乮1/4乯乸亖侾丂丂乮仼丂嶲峫 丗 乽幬岎嵗昗宯乿乯
丂丂偡側傢偪丄丂乮23/36乯倠亖侾丂傛傝丄丂倠亖36/23丂偲側傞丅
丂丂傛偭偰丄丂俙俧 丗 俧俽 亖 俀俁 丗 侾俁丂偱偁傞偙偲偑暘偐傞丅
丂傑偨丄丂仮俙俻俼 丗 仮俙俠俢 亖 侾 丗 俀丂偱偁傞偺偱丄
丂丂巐柺懱俙俹俻俼 丗 巐柺懱俙俛俠俢 亖 俙俹亊仮俙俻俼 丗 俙俛亊仮俙俠俢 亖 侾 丗 係
丂傛偭偰丄丂巐柺懱俙俹俻俼偺懱愊偼丄侾丂偲側傞丅
丂傑偨丄丂巐柺懱俙俹俻俼 丗 巐柺懱俽俹俻俼 亖 俙俧 丗 俙俽 亖 俀俁 丗 侾俁丂側偺偱丄
丂丂丂巐柺懱俽俹俻俼偺懱愊偼丄侾俁/俀俁丂偲側傞丅丂乮廔乯
乮僐儊儞僩乯丂慄暘偺挿偝傪巊傢偢丄斾偩偗傪梡偄偰懱愊傪媮傔偰偄傞偲偙傠偑僄儗僈儞僩偱
丂丂丂丂丂丂偡偹両
丂丂丂埲壓丄岺帠拞