斜交座標系（ｏｂｌｉｑｕｅ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ）は、通常の直交座標系を拡張したもので、
斜めに交差する２直線により、座標を定義しようとするものである。
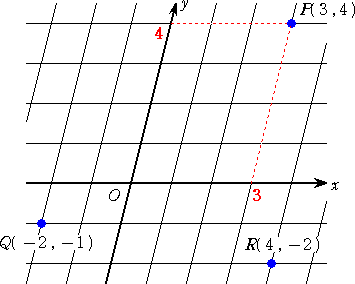
上図をしばらく眺めていると、直交座標系とほとんど変わらないこと、何となく直交座標系
を空間で斜めから見ているような雰囲気であることが分かるだろう。
直交座標系において、平面上の任意の点 Ｐ（ ｘ ， ｙ ） に対して、基本ベクトルを
ｅ1＝（ １ ， ０ ） 、 ｅ2＝（ ０ ， １ ）
とおくと、 ＯＰ＝ ｘｅ1 ＋ ｙｅ2 と一意に書くことができる。
ｅ1 、ｅ2 のように垂直でなくても大きさが １ でなくとも、一次独立な２つのベクトル ａ 、 ｂ
があれば、上記と同様に、平面上の任意の点 Ｐは、平面上に１点Ｏを固定して、
ＯＰ＝ ｘａ ＋ ｙｂ
と一意に書くことができる。
このとき、点 Ｐを表す座標として、（ ｘ ， ｙ ） としようとする考えが斜交座標系の考え方で
ある。
この斜交座標系という概念を知ると、平面図形に斜交座標系がオーバーラップし、いろい
ろな問題が解析幾何的に座標を用いて解けるような気分になるから不思議だ。
基本的な図形は、次のような条件で与えられる。斜交座標系の考え方を会得していれば
明らかだろう。
一次独立な２つの定ベクトル ＯＡ、OB に対して、 ＯＰ＝ｓＯＡ＋ｔＯＢ で点Ｐを定める。
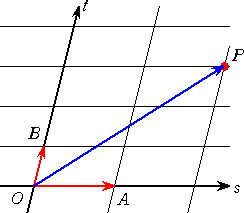
この場合、ＯＡ方向が、ｓ 軸（ＯＡの係数）、ＯＢ方向が、ｔ 軸（ＯＢの係数）であることに
注意を払わなければならない。
（１） ｓ＋ｔ＝１ のとき、動点 Ｐ の描く図形は、２点Ａ、Ｂを通る直線である。
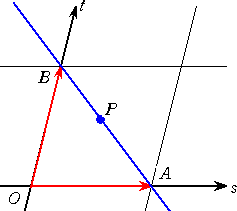
これは、
と書けることから、 点Ｐは、線分ＡＢを、 ｔ ： ｓ の比に分ける点である。
よって、動点 Ｐ の描く図形は、２点Ａ、Ｂを通る直線であるとしてもよい。
斜交座標系によらない場合は、一般的にこのように考えるのが定石である。
（２） ｓ＋ｔ＝１、 ｓ≧０、 ｔ≧０ のとき、動点 Ｐ の描く図形は、２点Ａ、Ｂを結ぶ線分である。
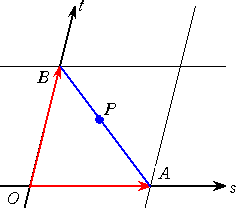
点Ｐは、線分ＡＢを、 ｔ ： ｓ の比に分ける点で、ｓ、 ｔ は同符号なので、点Ｐは線分
ＡＢの内分点となる。
よって、動点 Ｐ の描く図形は、２点Ａ、Ｂを結ぶ線分である。
（３） ｓ＋ｔ≦１、 ｓ≧０、 ｔ≧０ のとき、動点 Ｐ の描く図形は、△ＯＡＢの周および内部である。
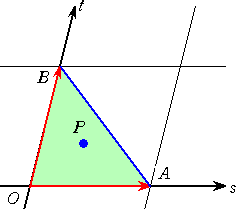
ｓ＋ｔ＝ｋ とおくと、 ０≦ｋ≦１ である。 ＯＡ’＝ｋＯＡ 、ＯＢ’＝ｋＯＢ とおくと、
Ａ’、Ｂ’はそれぞれ線分ＯＡ、ＯＢ上の点である。
さらに、 ｓ’＝ｓ/ｋ 、ｔ’＝ｔ/ｋ とおくと、
ＯＰ＝ｓ’ＯＡ’＋ｔ’ＯＢ’ ｓ’＋ｔ’＝１、 ｓ’≧０、 ｔ’≧０
が成り立つので、（２）より、動点 Ｐ の描く図形は、２点Ａ’、Ｂ’を結ぶ線分である。
０≦ｋ≦１ であるので、これらの線分は、△ＯＡＢの周および内部を埋め尽くす。
よって、動点 Ｐ の描く図形は、△ＯＡＢの周および内部である。
一次独立な２つの定ベクトル ＯＡ、OB に対して、 ＯＰ＝ｓＯＡ＋ｔＯＢ で点Ｐを定め、ｓ
と ｔ に様々な条件を付加して、点Ｐの存在範囲を問う問題は、教科書ではあまり深入りして
教えられることはないが、大学入試問題の１つの宝庫といってもいいだろう。
例えば、（解答は下記参照）
（１） 明治大学（２００７年）
∠ＡＯＢが直角で、ＯＡ＝ＯＢ＝１ である△ＯＡＢにおいて、ＯＰ＝ｓＯＡ＋ｔＯＢ とおく。
実数 ｓ 、ｔ が、 ｜ｓ｜＋｜ｔ｜≦１ を満たすとき、点Ｐが動く部分の面積を求めよ。
（答え： ２）
（２） 関西大学（２００７年）
平面上の３点 Ｏ、Ａ、Ｂ について、 ＯＡ＝２、ＯＢ＝３、ＯＡ⊥ＯＢ とする。このとき、
ＯＰ＝ｓＯＡ＋ｔＯＢ ２ｓ＋３ｔ≦５、 ｓ≧０、 ｔ≧０ で定められる点Ｐが動く領域の面
積を求めよ。 （答え： ２５/２）
（３） 横浜国立大学（２００６年）
平面上の３点 Ｏ、Ａ、Ｂ について、 ＯＡ＝５、ＯＢ＝６、ＡＢ＝７ とする。このとき、
ＯＰ＝ｓＯＡ＋ｔＯＢ で定められる点Ｐが次の条件を満たすとき、点Ｐが動く領域の面
積を求めよ。
（イ） １≦ｓ＋ｔ≦２、 ｓ≧０、 ｔ≧０ （答え： 18
）（ロ） １≦２ｓ＋ｔ≦２、 ｓ＋３ｔ≦３、 ｓ≧０、 ｔ≧０（答え： 27
/5）（４） 神戸大学（２０００年）
△ＯＡＢ について、ＯＰ＝（２ｓ＋ｔ）ＯＡ＋（ｓ−ｔ）ＯＢ ０≦ｓ＋ｔ≦１、 ｓ≧０、 ｔ≧０
で定められる点Ｐが動く領域の面積は△ＯＡＢの面積の何倍か。 （答え： ３倍）
（５） 東京都立大学（１９９７年）・・・現在は、首都大学東京
平面上に△ＡＢＣ と点 Ｏ がある。
ＯＰ＝ａＯＡ＋ｂＯＢ＋ｃＯＣ ａ＋ｂ＋ｃ＝１、 ａ≧０、 ｂ≧０、 ｃ≧０
で定められる点Ｐの描く図形を求めよ。 （答え： △ＡＢＣの内部と周）
これらは、斜交座標系の考えを用いれば、視覚的に即答できるだろう。
教科書で述べられる解法と斜交座標系の考えを用いた解法を、（２）関西大学（２００７）を
例題として比較してみよう。
（教科書的な解法） ＯＰ＝ｓＯＡ＋ｔＯＢ ２ｓ＋３ｔ≦５、 ｓ≧０、 ｔ≧０
２ｓ＋３ｔ≦５ より、 （2/5）ｓ＋（3/5）ｔ≦１ である。
そこで、 ｓ’＝（2/5）ｓ 、ｔ’＝（3/5）ｔ とおくと、 ｓ’＋ｔ’≦１、 ｓ’≧０、 ｔ’≧０
このとき、 ＯＡ’＝（5/2）ＯＡ 、ＯＢ’＝（5/3）ＯＢ とおくと、
Ａ’、Ｂ’はそれぞれ直線 ＯＡ、ＯＢ上の点で、
ＯＰ＝ｓ’ＯＡ’＋ｔ’ＯＢ’ ｓ’＋ｔ’≦１、 ｓ’≧０、 ｔ’≧０
が成り立つので、（３）より、動点 Ｐ の描く図形は、△ＯＡ’Ｂ’の周および内部である。
ＯＡ’＝２×５/２＝５、 ＯＢ’＝３×５/３＝５、 ＯＡ’⊥ＯＢ’ なので、求める面積は、
（１/２）×５×５＝２５/２
（斜交座標系による解法）
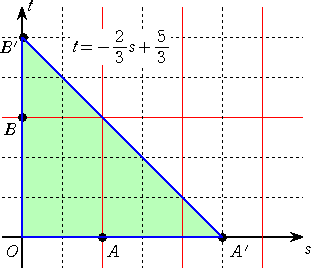点Ｐの存在範囲は、左図の領域で、求める面積は、
（１/２）×５×５＝２５/２
である。
（コメント） 「斜交座標系の考えを用いて・・・」と書けば、入試本番の記述式の解答としても
耐えうるのかな．．．？
上記の２つの解法を比較して、斜交座標系の考えが如何に有効かが理解できると思う。
大学入試問題（１）（３）（４）（５）についても、斜交座標系を用いた図を掲示しておこう。
（１）
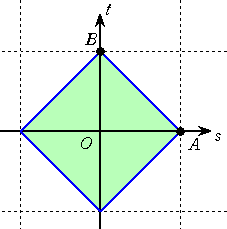
左図から、「面積 ２ 」は明らか！
（３）（イ）
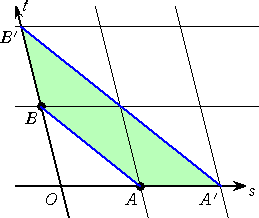ＯＡ＝５、ＯＢ＝６、ＡＢ＝７ より、ｃｏｓ∠ＡＯＢ＝１/５
よって、 ｓｉｎ∠ＡＯＢ＝2
/5 より、△ＯＡＢの面積は、 6
左図より、 △ＯＡ’Ｂ’＝４△ＯＡＢ＝24
よって、求める面積は、 18
（３）（ロ）
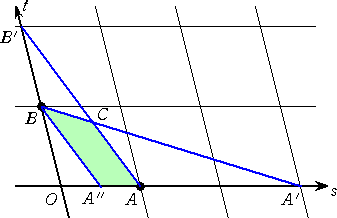△ＡＡ”Ｂ＝3 より、△Ａ’Ａ”Ｂ＝15
△Ａ’Ａ”Ｂ と △Ａ’ＡＣ の相似比は
５ ： ４ なので、
△Ａ’ＡＣ＝15
×（16/25）＝48/5よって、求める面積は、 27
/5（４） ＯＰ＝（２ｓ＋ｔ）ＯＡ＋（ｓ−ｔ）ＯＢ＝ｓ（２ＯＡ＋ＯＢ）＋ｔ（ＯＡ−ＯＢ）
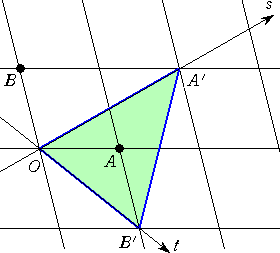ＯＡ’＝２ＯＡ＋ＯＢ 、ＯＢ’＝ＯＡ−ＯＢとすると、 ０≦ｓ＋ｔ≦１、 ｓ≧０、 ｔ≧０ なので、
求める面積は、△ＯＡ’Ｂ’の面積である。
ここで、 △ＯＡＡ’＝△ＯＡＢ’＝△ＯＡＢ
また、 △ＡＡ’Ｂ’＝△ＯＡＢ であるので、
求める面積は、△ＯＡＢの面積の３倍である。
（５） 大学受験の解答としては、
ＯＰ＝ａＯＡ＋ｂＯＢ＋ｃＯＣ において、 ｃ＝１−ａ−ｂ≧０ より、
０≦ａ＋ｂ≦１ 、 ａ≧０ 、 ｂ≧０ で、
ＯＰ−ＯＣ＝ａ（ＯＡ−ＯＣ）＋ｂ（ＯＢ−ＯＣ） すなわち、 ＣＰ＝ａＣＡ＋ｂＣＢ
よって、求める図形は、 △ＡＢＣの周および内部
となる。
斜交座標系を考えれば、「答えは一発！」だろう。
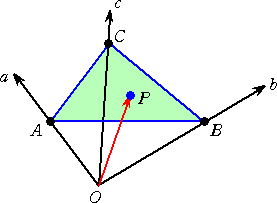
上記では、一次独立な２つの定ベクトル ＯＡ、OB に対して、
ＯＰ＝ｓＯＡ＋ｔＯＢ （ ｓ＋ｔ＝１ ）
で定められる点Ｐの描く図形が直線であることを見たが、逆に、２点Ａ、Ｂを通る直線が与
えられたとき、
ｓ＋ｔ＝１
という関係式が成り立つことも大切な考え方になる。これは、共線条件と言われる。
例 題 △ＡＢＣの辺ＡＢを ２ ： １ に内分する点をＰとし、線分ＰＣを ３ ： ２ に内分する点
をＱとする。直線ＡＱと辺ＢＣの交点をＲとするとき、ＢＲ ： ＲＣ を求めよ。
（解） ＡＰ＝（2/3）ＡＢ 、 ＡＱ＝（2/5）ＡＰ＋（3/5）ＡＣ より、
ＡＱ＝（4/15）ＡＢ＋（3/5）ＡＣ となる。
このとき、 ＡＲ＝ｔＡＱ＝（4/15）ｔＡＢ＋（3/5）ｔＡＣ （ ｔ は実数）と書ける。
Ｒ は、直線ＢＣ上の点なので、
（4/15）ｔ＋（3/5）ｔ＝１
よって、 ｔ＝15/13 となり、 ＡＲ＝（4/13）ＡＢ＋（9/13）ＡＣ である。
このとき、 ＢＲ ： ＲＣ ＝ ９ ： ４ となる。 （終）
（コメント） 直線上だから「ｓ＋ｔ＝１」という論法の美しさに、高校時代とても感動しました！