
日常生活で最も目にする図形、それは円柱ではないだろうか?このページでは、表面積
が一定な円柱の体積の最大値について調べようと思う。
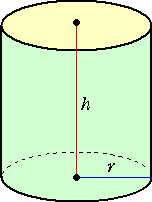
左図のように、底面の半径 r で高さ h の直円柱を考える。
表面積 S は一定とする。すなわち、
S=2πr2+2πrh (=一定) とする。
このとき、円柱の体積 V は、 V=πr2h
で与えられる。
S の値が一定という条件で、体積 V の最大値を求めることは、日常生活においても重
要な関心事であると信じる。
通常、この問題は、高校2年で学習する「数学II」の微分積分の格好の応用問題として、
教室で取り上げられることも多いことだろう。
(解) S=2πr2+2πrh より、 2πrh=−2πr2+S なので、 y=2V とおくと、
y=r(−2πr2+S)=−2πr3+Sr となる。
よって、 y’=−6πr2+S=0 とおくと、 r>0 に注意して、y は、
で極大、かつ最大となる。このとき、Vの最大値は、
となる。 (終)
ところで、表面積が一定のとき、体積が最大となる円柱とはいかなる形状をしているだろ
うか?体積の最大値そのものよりも、むしろこちらの方に実は興味がある。
2πrh=−2πr2+S=−2π{S/(6π)}+S=2S/3 なので、
このことから、円柱の体積が最大になるのは、上面、底面の円の中心を通る平面で円柱
を切断したとき、その切り口が正方形の場合であることが分かる。
(コメント) この結果は、直観的にも明らかかも...。
ここで、
とおく。( → この置き換えは、かなり有用な置き換えらしい!)
このとき、 S=2πr2+2πrh は、 r2+rh=3k2 と簡潔になる。
さらに、 V=−π(r3−3k2r) となり、これもまた見通しがよい式に変形できた!
上記の(解)では、体積 V の最大値を求めるために微分法を活用したが、微分を用いず
に、次のような計算をしても求められることに驚かされる。
V−2πk3=−π(r3−3k2r+2k3)=−π(r−k)2(r+2k)≦0
上記の不等式から、体積 V は、 r=k のとき最大で、最大値 2πk3 をとる。
このときの円柱の高さは、 rh=3k2−r2=3r2−r2=2r2 より、 h=2r となる。
(コメント) 2πk3 との差を考えるところがポイントかな?何となくスッキリしたような、しない
ような...そんな気分ですね!
以下、工事中