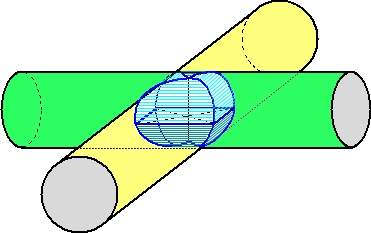
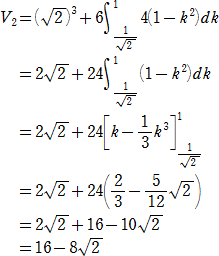直交する円柱 
平成２１年１０月１日付けで当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんが次の問題
を「腕試し」と称して当ＨＰの掲示板「出会いの泉」に出題された。
半径が１の２つの円柱が直交する物体がある。この共通部分の体積V1はいかほど
か？
また、半径が１の３つの円柱が１ヶ所で互いに直交する物体がある。この共通部分
の体積V2はいかほどか？
この問いかけに対して、平成２１年１０月４日付けで、ペントミノさんが解答を寄せられた。
（ペントミノさんの解答・・・一部文言等を修正させていただきました）
[１] ２つの円柱の場合
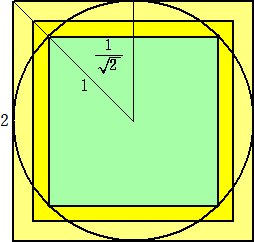
円柱の中心軸を ｘ、ｙ とし、原点で直交しているものとする。このとき、平面 ｚ＝ｋ で切
断してできる図形は正方形である。（下図は切り口の正方形の１/４の正方形）
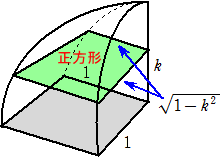よって、断面積は、 ４（１−ｋ2）
となる。
これを、 ｋ＝−１〜１で積分して体積が得られる。
すなわち、
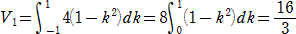
[２] ３つの円柱の場合
円柱の中心軸を ｘ、ｙ、ｚ とし、原点で直交しているものとする。このときでき上がる物体
は、１辺の長さが
の立方体に、[１]の物体の ｋ＝１/
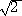〜１ の部分だけ切り出したもの
を立方体の各面に貼り合わせたものになるから、以下のように体積が求められる。
「どちらもπが出てこないところが面白いですね。」と、ペントミノさん。
物体のイメージがつかみにくい場合は、工作してみよう。
[１]であれば、 ｙ＝±ｓｉｎ ｘ (０≦ｘ≦π) で囲まれる図形を４枚用意し、貼り合わせる。
[２]であれば、 ｙ＝±ｓｉｎ ｘ 、ｙ＝±ｃｏｓ ｘ (０≦ｘ≦π/２) で囲まれる図形を１２枚用
意し、貼り合わせる。
（→ 参考：「円柱の切り口」）
このことから、表面積も容易に求められる。
[１]の物体の場合は、 Ｓ1＝16 、 [２]の物体は、 Ｓ2＝４８−２４
である。
ここで、 Ｖ1 ： Ｓ1 ＝ Ｖ2 ： Ｓ2 ＝ １ ： ３ となる点が気になったので、
１辺が２の立方体 、半径１で高さ２の円柱 、[１]の物体 、[２]の物体 、半径１の球
の体積と表面積をまとめてみた。
| 物 体 |
体 積 |
表 面 積 |
| １辺が２の立方体 |
８ |
２４ |
| 半径１で高さ２の円柱 |
２π |
６π |
| [１]の物体 |
１６/３ |
１６ |
| [２]の物体 |
１６−８ |
４８−２４ |
| 半径１の球 |
４π/３ |
４π |
いずれも、体積 ： 表面積 ＝ １ ： ３ になりました。（偶然なのか、必然なのか・・・？）
この件で、らすかるさんから（平成２１年１０月４日付け）：
必然だと思います。ちょっとうろ覚えですが、
「すべての面が接する内接球が存在する多面体」の表面積は、体積を内接球
の半径で微分したものになる
んだったと思います。求められた物体は、いずれも条件を満たす多面体（の極限）と考
えられ、ｒ3 を微分して、３ｒ2 ですから、ｒ＝１ なので、３倍になりますね。
これを受けて、ペントミノさんから（平成２１年１０月５日付け）：
らすかるさん、解説ありがとうございます。勉強になります。私も昨日投稿してから、次
のようなことを考えていました。
表面積を微小面積に分割し、その微小面積を底面に、物体の中心を頂点とする錐を
考えると、その錐の高さはどの微小面積に対しても常に1で、物体の体積はその錐を
全表面積にわたって積分すれば求められ、 体積＝(１/３)＊表面積 になると！
（コメント） なるほど！ペントミノさんの考え方に「Ｂｉｎｇｏ！」ですね。
私自身は、次の体積比が同じになることにも美しさを感じます．．． ｆ(^^;) 。
半径１で高さ２の円柱 ： 半径１の球 ＝ ３ ： ２
１辺が２の立方体 ： [１]の物体 ＝ ３ ： ２
