ピタゴラスの定理とその拡張 
我が国の数学教程によれば、ピタゴラスの定理は中学3年で学習する。この定理は、図
形的にも大切な定理であるが、2点間の距離の計算とか計量にも関係してきて、解析幾何
的にも、その後の数学の学習においても、重要な定理である。
しかしながら、その重要性にも関わらず、昨今の高校生にとって、このピタゴラスの定理
が、平方根の計算でつまずいて使いこなせない、もしくは定理そのものの存在を知らない
という驚くべき生徒も出現していて、今、高校数学は憂慮すべき事態に陥っている。その責
は学習指導要領によるばかりでなく、彼らをこれまで指導してきた人々、彼らを取り巻く社
会環境、そして、彼ら自身の数学に対する意識の有り様など原因は複合していて特定でき
ない。
私的に考えれば、現在の数学教育の問題点は、基礎基本にばかり重点をおいて、応用
を教えないところにあると思う。いくら立派なことを学んでも、それを実際に使いこなす場が
ないと、本当の意味が分からない。学習指導要領が変わるたびにどんどん応用分野が削
られてきた。微分方程式とか積分の応用、空間図形など是非復活させて欲しいと思う。
いろいろな場面場面で知っている知識を総動員して立ち向かうという経験が、今求められ
ている。そのような趣旨で、新学習指導要領では、「総合的な学習の時間」というものが設
けられたが、その時間分、基本教科の授業時数が削られ、基礎基本を習熟しないまま応用
に入るという問題を抱えている。やはり、基本教科の授業時数をしっかり確保し、その中で、
基本から応用まできっちり鍛えるというスタイルが好ましいと私は考える。
さて、前置きが長くなってしまったが、このページではピタゴラスの定理とその拡張(?)に
ついて、まとめてみたいと思う。
ピタゴラスの定理(三平方の定理)
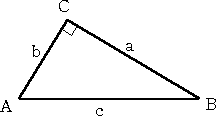 |
左図のような直角三角形ABCにおいて、
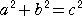
が成り立つ。
逆に、上式が成り立つような3辺 a,b,c をもつ三角形
は直角三角形である。 |
この定理の証明は、百以上知られているらしい。
三平方の定理がどのように使われるか、例えば、巣鴨中学(2021)で出題された入試問
題で見てみよう。(問題は、一部改題)
問題 下図の△ABCにおいて、AB=4、AC=6、∠B=2∠Cである。このとき、辺BCの
長さを求めよ。
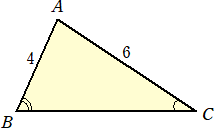
(解) 下図のように、辺BC上に、AB=ADとなる点Dをとり、Aより辺BCに下ろした垂線の
足をHとする。
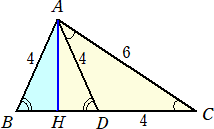
BH=x とおくと、 AH2=42−x2=62−(x+4)2 が成り立つ。
展開して整理すると、 8x=4 より、 x=1/2
よって、 BC=2x+4=5 (終)
上記のような図形の計量問題で、三平方の定理は大活躍する。直角を作ることがポイント
だろう。定理の有用性に感動されることと思う。
ここでは、このページの目標である「拡張」を意識して次の図を掲げる。この図は、ユーク
リッドによる理論的な証明に用いられたらしい。証明の難しさから、英仏の学生たちは、「ロ
バの橋」と呼んで敬遠したそうだ。
(注) 「ロバの橋」という名は、18、19世紀のイギリスのオックスフォード大学、ケンブリッジ
大学の学生たちに知られていた。難解なユークリッド幾何で多くの学生が落ちこぼれたが、
「落ちこぼれ」てしまうほど難しいものを、「ロバの橋」と呼んだようだ。ロバ、つまり、愚か
なものが落ちる橋というところからつけられたらしい。
(参考文献) 仲田紀夫 著 意外に役に立つ数学67の発見(黎明書房)
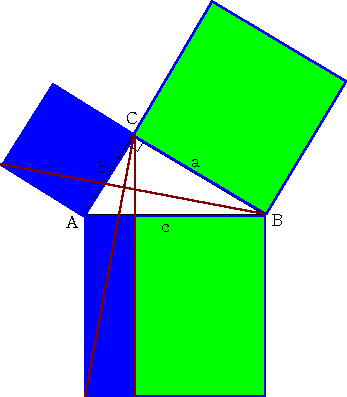
等積変形と三角形の合同により、上図の同じ色の部分の面積は等しい。
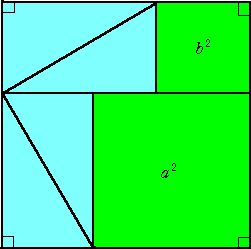
ピタゴラスの定理の証明の中で最も簡明な証明は、次の図であろう。

直角三角形の辺上に正方形を作るかわりに、平行四辺形を作って、ピタゴラスの定理を
拡張した人がいる。その人の名は、パップスである。
三角形は一般の三角形としてよい。
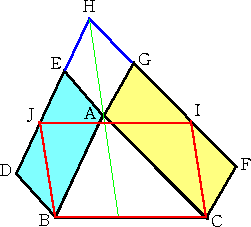 |
左図のように、AB、ACを一辺とする任意の平行
四辺形を作り、DEとFGの交点をHとする。
さらに、辺DE上に点Jをとり、四角形ABJHが平
行四辺形であるようにする。同様に、辺FG上に点
I をとり、四角形ACIHが平行四辺形であるように
する。
|
このとき、次が成り立つ。
平行四辺形BCIJの面積=平行四辺形ABDEの面積+平行四辺形ACFGの面積
(証明)は、等積変形から明らかであろう。
ピタゴラスの定理の拡張として、上記以外に、いろいろなものが知られている。
(1) 直角三角形の3辺上の相似図形について、斜辺上の図形の面積は、他の2辺の上
の図形の面積の和に等しい。
(2) ヒポクラテス(Hippocrates)の定理・・・こちらを参照
(3) 余弦定理 ・・・ 三角形において、 a2=b2+c2−2bc・cosA
(4) 中線定理 ・・・ 三角形ABCにおいて、辺BCの中点をMとする。このとき、
AB2+AC2=2(AM2+BM2)
(→ 参考 : スチュワートの定理 中線定理の証明は、「適切な座標系」を参照)
(5) トレミー(Ptolemy)の定理 ・・・ 円に内接する四角形ABCDにおいて、
AB・CD+AD・BC=AC・BD
意外なものが、実はピタゴラスの定理の拡張になっていて、今まで気づかなかったことに
正直驚いている。皆さんは、ご存知でしたか?
(参考文献:船山良三 著 身近な数学の歴史(東洋書店)
遠山 啓 著 数学入門(上)(岩波書店)
清宮俊雄 著 幾何学(科学新興社))
当HPの読者のK.S.さんより、「ピタゴラスの定理の拡張」についての話題をメールで頂
いた。(平成24年3月28日付け)
xyz空間において、線分を x軸、y軸、z軸上に射影した長さをそれぞれ
a、b、c とすれば、
線分の長さ s は、 s2=a2+b2+c2 で与えられる。
特に、c=0 のとき、つまり、平面 z=0 と平行な平面上に線分があるとき、ピタゴラスの
定理と考えることができる。 一般の曲面上の長さについて、微分幾何において、
ds2=Adx2+Bdxdy+Cdydx+Ddy2
特に、A=D=1、B=C=0 ならば、ユークリッド平面となり、ピタゴラスの定理を得る。
空舟さんからのコメントです。(平成24年4月7日付け)
3次元空間では、3点 A(a,0,0)、B(0,b,0)、C(0,0,c) について、
(△OAB)2+(△OBC)2+(△OCA)2=(△ABC)2
が成り立ち、高次元でも実は同様のことが成り立ちます。
例えば、4次元空間上の4点 A(a,0,0,0)、B(0,b,0,0)、C(0,0,c,0)、D(0,0,0,d) に
ついて、ABCDの4点を含む3次元空間があるので、三角錐ABCDの体積は自然に定義され
ますが、その二乗が三角錐OABC、OBCD、OCDA、ODAB の体積の二乗和に一致するとい
うのが主張です。
(コメント) 参考 → 「正射影・空間の必須技法」
土筆の子さんからのコメントです。(平成24年4月8日付け)
ピタゴラスの定理とその拡張の話題がありましたので、別の話ですが、メモしておきます。
X2+Y2=Z2+W2 の整数解は、X=ab-cd、 Y=ad+bc、 Z=ab+cd、 W=ad-bc の a、b、c、d
の
ところに勝手な整数を代入すれば好きなだけ得られるとのこと。
W=0 は、ピタゴラス数。よく知られた以下の式との関係を見てみる。
(m2-n2)2+(2mn)2=(m2+n2)2
ad-bc=0 より、 d=bc/a で、
X=ab-cd=ab-(b/a)c2 、 Y=ad+bc=2bc 、 Z=ab+cd=ab+(b/a)c2
ここで、 ab=m2 、 (b/a)c2=n2 としてよい。m=√(ab) 、n=c・√(b/a) とすると、確かに、
2mn=2bc となり、 X=m2-n2 、Y=2mn 、Z=m2+n2 が成り立っている。
W=1 は、ad-bc=1 を考えることになる。行列{{a,b},{c,d}}の行列式が1になることと同じで、こ
の性質をもった整数行列は数論では非常に大事な対象とのことです。
(参考) 硲 文夫 著 「代数幾何学」(森北出版(株))
k.nika さんからのコメントです。(平成24年4月9日付け)
ピタゴラスの定理ではないのですが、 X2+Y2=AX+B という式で、A、Bに具体的な数
値が与えられたとして、X、Yを求める何か良い方法はないでしょうか?
AX+B のXに、1、2、3、・・・と代入して、その答えを素因数分解して、4を法として3に
合同な素因数が全て平方(冪指数が偶数)になっている事を調べるしかないのでしょうか。
らすかるさんからのコメントです。(平成24年4月9日付け)
Xに順番に値を代入しなくても、 (2X−A)2+(2Y)2=A2+4B と変形できますから、
A2+4B を平方数の和に分解出来れば、X、Yは求まりますね。
k.nika さんからのコメントです。(平成24年4月9日付け)
有難うございます。この方法で計算を進めてみます。
(追記) 平成24年8月29日付け
平成24年8月23日付けで、当HP読者のK.S.さんより、ピタゴラスの定理の拡張に関
連する話題をメールで頂いた。
ピタゴラスの定理の拡張で、「角の二等分線定理 AD×AD=AB×AC−BD×CD」が、
特に、二等辺三角形のとき、ピタゴラスの定理が成り立つ。
「ピタゴラスの定理」「余弦定理」「トレミーの定理」「角の二等分線定理」「中線定理」など幾
何的な証明がありますが、これらをそれぞれ直接に代数的に証明できるのではないでしょう
か?皆さんのお力を借りたいと思います。
(コメント) 上記のことを追認してみた。
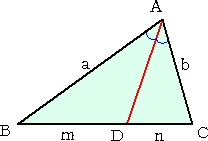 |
a=b のとき、 m=n で、∠ADB=90°である。
このとき、 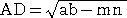 から、 から、
AD2=a2−m2 すなわち、
AD2+BD2=AB2
が成り立つ。(ピタゴラスの定理) |








