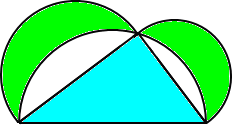
辺を直径とする半円が3個描かれている。
このとき、2つの月形の面積の和と直角三角形
の面積は相等しい。
(この図形は、「ヒッポクラテスの三日月」(B.C.5〜4) と言われる。)
・月形の面積の不思議 S.H氏
 |
左図のように水色の直角三角形があり、その各 辺を直径とする半円が3個描かれている。 このとき、2つの月形の面積の和と直角三角形 の面積は相等しい。 (この図形は、「ヒッポクラテスの三日月」(B.C.5〜4) と言われる。) |
「本当にそうかな?」と思って計算してみた。
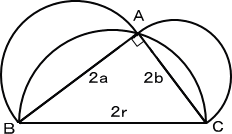 |
左図において、三平方の定理より、 4a2+4b2=4r2 故に、a2+b2=r2 が成り立つ |
このとき、(2つの月形の面積の和)
=(1/2)πa2+(1/2)πb2+2ab−(1/2)πr2
=(1/2)π(a2+b2−r2)+2ab
=2ab
=(直角三角形の面積)
以上計算では納得せざるをえないが、とても不思議な現象だ。
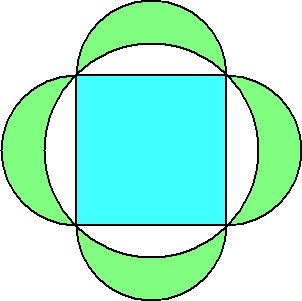
上記の図形を2つ並べれば、同様のことが言えることは明らかだろう。
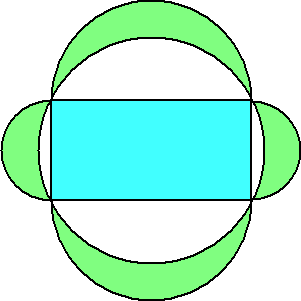
上記は長方形だが、正方形にした方が美しいかな?