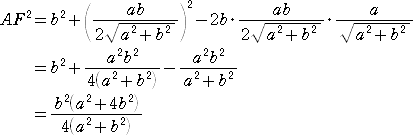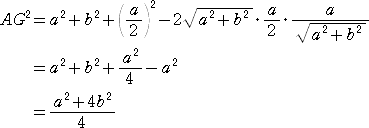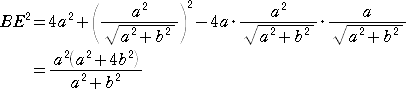適切な座標系 
平面幾何では、補助線を引いて図形の種々の性質から新たな図形の性質を証明するこ
とが最も美しいとされる。それが平面幾何の醍醐味であると考える方も多いだろう。しかし、
図形の性質のみに頼って問題を解こうとする場合、ある種の限界を感じることが少なから
ずあり、そういう思いを経験した方も多いに違いない。
そんなときは、座標系を用いたりベクトルを用いたりと、解析幾何の手法に頼る場合が多
く、しかも比較的容易に解決される。算数の問題に高等数学を用いるようで後味は悪いが、
そのことによって図形の性質のみに頼っては見えなかった新たな視点を獲得することが出
来るわけで、ま~一長一短というところだろう。
平面幾何では中線定理が重要な性質であるが、解析幾何を説明する材料として、高校数
学では重宝がられている。
中線定理
△ABCにおいて、辺BCの中点をMとする。
このとき、
AB2+AC2=2(AM2+BM2) |
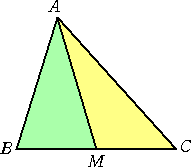 |
いくつかよく知られた証明をまとめておこう。
(三平方の定理を利用する証明)
頂点Aより底辺BCに垂線を下ろし、その足をHとする。
このとき、 AB2+AC2=AH2+HB2+AH2+HC2=2AH2+HB2+HC2
ここで、 HB2+HC2=(BM-HM)2+(HM+MC)2
=(BM-HM)2+(HM+BM)2
=2(BM2+HM2)
AH2+HM2=AM2
なので、 AB2+AC2=2( AH2+BM2+HM2)=2( AM2+BM2) (証終)
(余弦定理を利用する証明)
△ABMにおいて余弦定理より、 AB2=AM2+BM2-2AM・BM・cos∠AMB
同様に、△ACMにおいて、 AC2=AM2+CM2-2AM・CM・cos∠AMC
ここで、 BM=CM 、 cos∠AMC=-cos∠AMB なので、
AC2=AM2+BM2+2AM・BM・cos∠AMB
よって、 AB2+AC2=AM2+BM2-2AM・BM・cos∠AMB
+AM2+BM2+2AM・BM・cos∠AMB
=2( AM2+BM2) (証終)
(座標系を利用する証明)
M( 0 , 0 )、A( a , b )、B( -c , 0 )、C( c ,
0 ) とする。
このとき、 AB2+AC2=(a+c)2+b2+(a-c)2+b2=2(a2+b2+c2)
2( AM2+BM2)=2(a2+b2+c2)
よって、 AB2+AC2=2( AM2+BM2) (証終)
(ベクトルを利用する証明)
MA=a 、MA=b とおくと、
AB2+AC2=|a-b|2+|a+b|2
=|a|2-2a・b+|b|2+|a|2+2a・b+|b|2
=2(|a|2+|b|2)
=2( AM2+BM2) (証終)
(追記) 平成25年3月15日付け
上記のように、いろいろな方法で示された中線定理であるが、その逆は当然成り立たない。
実際に、AB=a 、AC=b 、AM=m について、中線定理が成り立つとすれば、
|a|2+|b|2=2(|m|2+|m-a|2)
これより、 |a|2+|b|2=4|m|2-4m・a+2|a|2
|m|2-m・a=(|b|2-|a|2)/4
よって、 |m-a/2|2=|b|2/4 が成り立つ。
すなわち、中線定理が成り立つとき、点Mは上記のベクトル方程式を満たす点である。
△ABCの辺ABの中点を中心として、半径|b|/2 の円周上の点なら、必ず成り立つ。
中点連結定理より、ちょうどそのうちの1点に、辺BCの中点が入っているわけである。
さて、いよいよこのページの本題に入ろう。
上記では、辺BCの中点を原点とし、辺BCを軸とする座標系を考えた。基本的に座標系
は自由に選べるが、もちろん、その問題に適切な座標系というものが存在する。計算力が
ある方は全く苦にならない程度の差ではあるが、決められた時間内に解かなければならな
い場合は、その選択により明暗が分かれるかもしれない。
次の問題に対して、読者の方はどのように座標系を設定するであろうか?
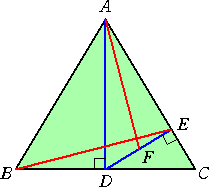
左図のような、AB=ACの二等辺三角形ABCにおいて、
頂点Aより辺BCに垂線ADを下ろし、さらに点Dより辺AC
に垂線DEを下ろす。線分DEの中点を F とするとき、
AF⊥BE が成り立つことを証明せよ。
この場合に最も適切な座標系は、下図のように設定するものである。とても斬新な設定
で驚かされる。読者の皆さんは正解でしたか?
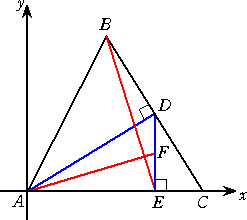
(証明) A( 0 , 0 )、B( 4a , 4b )、C( 4c , 0 ) とすると、 a2+b2=c2 で、
D( 2a+2c , 2b ) 、E( 2a+2c , 0 ) 、F(
2a+2c , b )
となり、線分OFの傾きは、 b/(2a+2c) で、線分BEの傾きは、 2b/(a-c)
また、線分AFの傾きは、 b/2(a+c) なので、
傾きの積は、 2b/(a-c)×b/2(a+c)=b2/(a2-c2)=b2/(-b2)=-1
したがって、 AF⊥BE が成り立つ。 (証終)
上記のように計算できることにはなかなか気がつかず、普通は下記のような計算で終わ
りにしている方が多分多いことだろう。
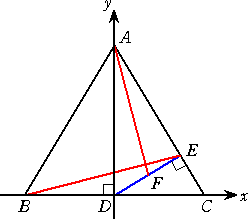 |
左図において、 A( 0 , a ) 、B( -b , 0 ) 、
C( b , 0 )、 D( 0 , 0 ) とする。
直線ACの方程式は、ax+by=ab で、直線DE
の方程式は、bx-ay=0 なので、
E( a2b/(a2+b2) , ab2/(a2+b2) )
よって、
F( a2b/{2(a2+b2)} , ab2/{2(a2+b2)} ) |
このとき、直線AFの傾きは、 -(2a2+b2)/{ab}
直線BEの傾きは、 ab/{2a2+b2}
となるので、 傾きの積が-1 より、AF⊥BE が成り立つ。 (証終)
(コメント) 両者の解を比較して、座標系の設定如何によってこれほど計算が簡略化され
るのかと、感動を覚える。
平面幾何の問題は、ベクトルを用いるのが受験生の一般的な解法だろう。ベクトルは座
標系を意識することなく解くことができる。
 (証明) 左図において、 DA=a、DC=b、DF=c
(証明) 左図において、 DA=a、DC=b、DF=c
とすると、 a・b=0 、c・(a-b)=0
このとき、 (a-c)・(b+2c)
=a・b+2a・c-b・c-2c・c
=a・c-2c・c
=(a-2c)・c
=EA・DF
=0
よって、 AF⊥BE が成り立つ。 (証終)
(コメント) 平面幾何の問題に座標やらベクトルを使うのは、ある意味で敗北である。図形
の性質のみでやはり解きたい!現在、その解法を模索中である。
平成20年2月17日付けで、当HPの掲示板「出会いの泉」に、HN「ひと」さんが初等幾何
的証明を書き込まれた。三角形の相似を用いたものである。
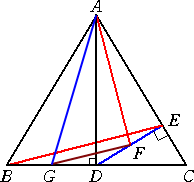 左図のように線分BDの中点を G とし、2点 F、G
左図のように線分BDの中点を G とし、2点 F、G
を線分で結ぶ。
このとき、 △ABD ∽ △AGF である。
(「ひと」さんから寄せられた証明には、この部分の証明がなかった。
実は、この部分が、この問題の核心の部分である。図形的証明を
何日間か考えたが、どうしてもその方法を発見することが出来なか
った!...ホントにないのかな?)
線分の長さを直接計算するという、非常に泥臭い、出来れば避けたい証明に甘んじるこ
とにしよう。
BD=DC=a 、AD=b 、∠DCE=θ とおくと、 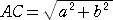 なので、
なので、
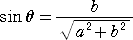
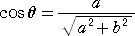
このとき、
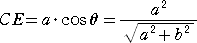
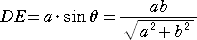
まず、
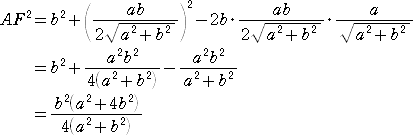
なので、
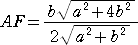
よって、

同様にして、
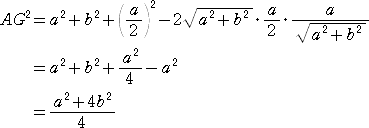
なので、
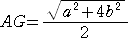
よって、
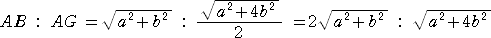
また、
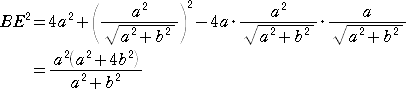
なので、
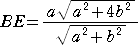
すなわち、中点連結定理より、BE=2GF なので、
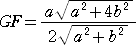
よって、
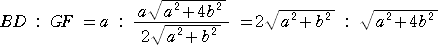
以上から、△ABDと△AGFにおいて、対応する3辺の比が等しいので、
△ABD ∽ △AGF
である。よって、 ∠ADB=90°より、∠AFG=90°となる。
ここで、中点連結定理より、BE//GF であるので、 AF⊥BE が成り立つ。
(コメント) 三角形の相似を示すのに3辺の比を用いたのは、もしかしたら初体験かも?
(追記) 平成20年2月26日付け
上記では、3辺の比相等による相似を示したが、当HPの掲示板「出会いの泉」で「ひと」
さんから、回転縮小の一次変換を活用するといいというご指摘をいただいた。
△ABD ∽ △ADE なので、Aを中心とする、BをDに移すような回転縮小の一次変換を
考えると、DはEに移る。したがって、BDの中点GはDEの中点Fに移る。
よって、BがDに移り、GがFに移り、∠BAD=∠GAF なので、△ABD ∽ △AGF が
成り立つ。 よって、 ∠ADB=90°より、∠AFG=90°となるので、 AF⊥BE が成り
立つ。
(コメント) 3辺の比相等ではさすがに腕力に物を言わせてねじ伏せた感が否めませんが、
2辺の比とその間の角相等を用いると証明が美しくなりますね!すっきりした証明
で感動しました。「ひと」さんに感謝いたします。
(追記) 当HP読者のHN「のぼりん」さんから、「△ABD∽△AGF」を示さなくても「AF⊥BE」
は示されるとメールでご教示いただきました。(平成27年12月28日付け)
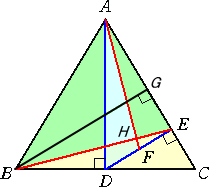 |
BからACに下ろした垂線の足をG、BEとAFの交点をH
とする。このとき、
CE=EG、DF=FE、△BGC∽△ADC∽△AEDだから、
∠BCE=∠ADE、BC:AD=CE:DF より、
△CBE∽△DAF (2辺の比と夾角相等) が成り立つ。 |
よって、∠AHB=180°−∠BAH−∠ABH
=180°−(∠BAD+∠DAF)−(∠ABD−∠CBE)
=180°−∠BAD−∠ABD=90°
(コメント) 別な視点からの証明をいただき、のぼりんさんに感謝します。のぼりんさんの解
法の指針を参考にさせていただいて、次のように、△ABD ∽ △AGF が示される
ことに気づかされました。重ねて、のぼりんさんにお礼申し上げます。
 |
左図において、 △ABD∽ △ADE なので、
AB:AD=AG:AF 、∠BAD=∠GAF
よって、2辺の比と夾角相等により、
△ABD ∽ △AGF |
HN「ひと」さんも多分上記のような推論で、「△ABD ∽ △AGF」を示されたのだと思う。
ちょっと解答を読み切れず、HN「ひと」さんにご迷惑をおかけしました。お詫びいたします。
以下、工事中

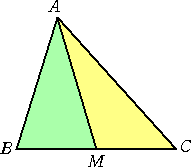



 左図のように線分BDの中点を G とし、2点 F、G
左図のように線分BDの中点を G とし、2点 F、G