ピタゴラスの定理とその証明　　　　　　　　　　　　　

　中学３年で学習するピタゴラスの定理（三平方の定理）は、その後の数学の学習で繰り
返し用いられる重要な定理である。

　ピタゴラスの定理（三平方の定理）

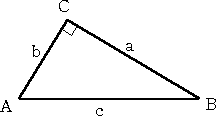左図のような直角三角形ＡＢＣにおいて、 　　ａ2＋ｂ2＝ｃ2 　が成り立つ。 　　逆に、上式が成り立つような３辺 ａ，ｂ，ｃ をもつ三角 　形は直角三角形である。

　ピタゴラスの定理の覚え方としては、

　斜辺の平方は他の２辺の平方の和

が最も優れているだろう。

　昨今の生徒の意識として、結果さえ覚えればＯＫで、その成り立ち等に関心を払わない
場合が多い。

　このピタゴラスの定理（三平方の定理）の証明は、百以上知られている。その全てを紹
介することは困難であるが、定理が成り立つことを納得する一つの方法として、その証明
のいくつかに触れることは今後の学習において有効と考える。

　当ＨＰがいつもお世話になっている未菜実さんからの情報によると、

　Pythagorean Teorem

というＨＰサイトに、たくさんのピタゴラスの定理（三平方の定理）の証明がまとめられてい
るという。これは、３類生さんから質問があった、「よくこの証明方法は１００種類以上ある
と言われますが本当にそんなにあるのでしょうか？私は今までそんなにたくさん載せた本
やＨＰなどは見たことがないのですが・・・。」（平成１７年１２月７日付け）を受けてのもので
ある。情報を頂いて、未菜実さんに感謝いたします。


　このページでは、興味ある証明を徒然なるままに鑑賞していきたいと思う。

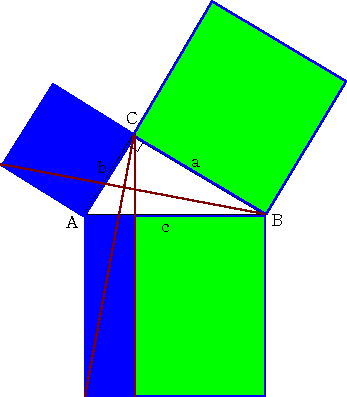
証明１　　等積変形と三角形の合同により、下図の同じ色の部分の面積は等しい。
　　　　　（この証明方法は、ユークリッドによるものと言われている。）

　

　上記のユークリッドによる証明と似ているが、ヘルマン・フォン・バラヴァツレによる次の証
明も等積変形を利用するもので味わい深い。数ある証明の中でも特にダイナミックな証明と
されている。

　

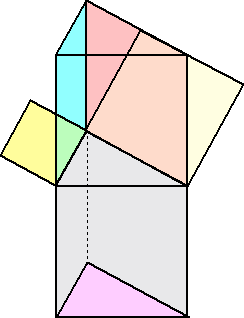
証明２　　　図形を組み替えることにより、下図の同じ色の部分の面積は等しい。

　　　　　　　

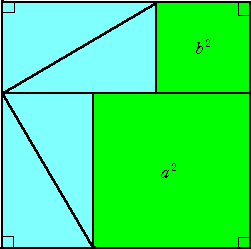
　講演「広中平祐の、ちょっと元気になる話」（協和発酵）によれば、この方法が、ピタゴラス
による証明法とのことである。

　左図の正方形の面積は、　（ａｂ/２）×４＋ｃ²＝２ａｂ＋ｃ²

一方、左図の図形を組み替えた右図の正方形の面積は、　２ａｂ＋ａ²＋ｂ²

よって、　２ａｂ＋ｃ²＝２ａｂ＋ａ²＋ｂ²　から、　ａ²＋ｂ²＝ｃ²　が成り立つ。


証明３　　　内接円の半径を巧妙に利用する証明。

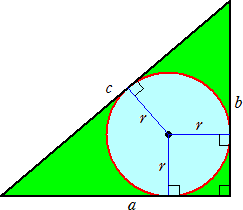	左図の三角形の面積は、 　　（ａ＋ｂ＋ｃ）ｒ/２＝ａｂ/２ 　　すなわち、（ａ＋ｂ＋ｃ）ｒ＝ａｂ 　　　さらに、接線の長さは等しいので、 　　　ｃ＝（ａ−ｒ）＋（ｂ−ｒ）＝ａ＋ｂ−２ｒ 　　よって、ｒ＝（ａ＋ｂ−ｃ）/２　を上式に代入して、 　　（ａ＋ｂ＋ｃ）（ａ＋ｂ−ｃ）＝２ａｂ
したがって、　　　　が成り立つ。

証明４　　　合同な図形を巧妙に利用する証明。
　　　　　　（この証明方法は、レオナルド・ダ・ビンチによるものと言われている。）

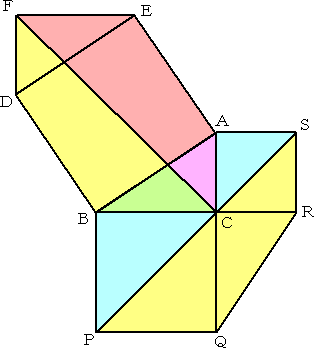左図において、四角形ＥＦＣＡ、ＦＤＢＣ、 　ＡＢＰＳ、ＰＱＲＳの面積は全て等しい。 　　このことから、五角形ＦＤＢＡＥと凹七角 　形ＡＣＢＰＱＲＳの面積は等しい。 　　ここで、△ＥＦＤと△ＱＣＲの面積は等し 　いことに注意。 　　よって、正方形ＤＢＡＥの面積は、 　２つの正方形　ＢＰＱＣ　と　ＡＣＲＳ　の 　面積の和に等しい。

証明５　　　台形の面積を利用する証明。
　　　　　　（この証明方法は、ガルフィールド（米第２０代大統領）によるものと言われている。）

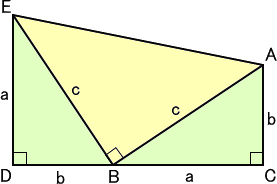左図において、台形ＡＣＤＥの面積は、 　　　　（ａ＋ｂ）2/２　　で、また、 　　　　　台形ＡＣＤＥ＝２△ＡＢＣ＋△ＡＢＥ　 　　　　なので、 　　　　　（ａ＋ｂ）2/２＝ａｂ＋ｃ2/２ 　　　　よって、　　が成り立つ。

証明６　　　図形の組み替えによる証明。
　　　　　　（この証明方法は、バスカラ（インド）によるものと言われている。）

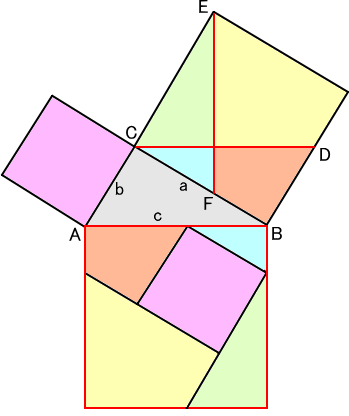左図のように、頂点Ｃ、Ｅより、直交 　する２つの線分を引き、辺との交点を 　Ｄ、Ｆとする。 　　このとき、　ＣＤ＝ＥＦ＝ｃ　であり、 　ＣＦ＝Ｂ　である。 　切り分けられた図形をそれぞれ組み 　替えると、斜辺の長さを一辺とする正 　方形が埋め尽くされる。 　この図形の切り分けによる証明は、 他にもたくさん知られている。 　平成１７年７月２３日（土）、特番 「世界一受けたい授業」（日本テレビ系） での秋山　仁　先生による「ピタゴラスの 定理」の証明もその一つだ。

　秋山先生は、何とわずか ７ 秒で、数式を使わずに、ピタゴラスの定理を証明された。

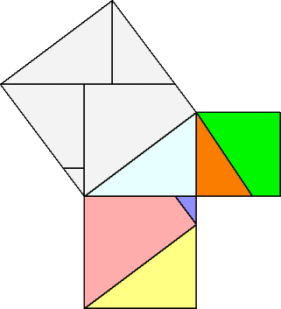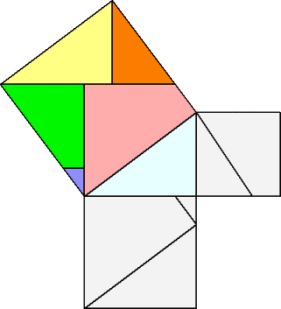　左の図形を回転させていくと、色分けされた図形が「ストン、ストン、・・・」と右図のように
入っていく様になっていた。

　上図では、いろいろな図形が絡んでいて分かりにくい印象があるが、最近、秋山　仁先生
がＮＨＫ高校講座「数学基礎」で非常に分かりやすく説明されていた。

　次の図が基本になるのだという。

　

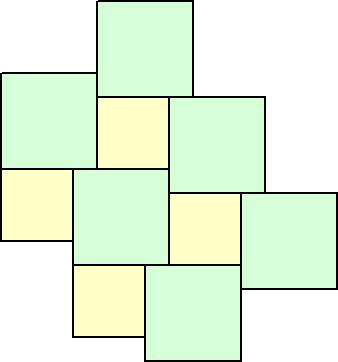
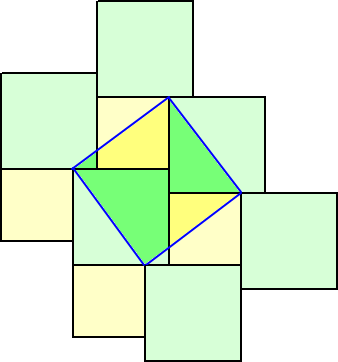
　上図の図形に対して、下図のように正方形の頂点を結んで新しい正方形を作図すると、
証明６の本質が見えてくる。（秋山先生に、謝謝！）

　

証明７　　　相似比の利用による証明。
　　　　　　（この証明方法は、アインシュタインによるものと言われている。）

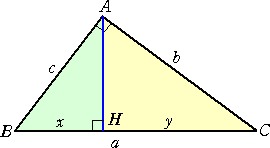左図において、 　　ａ ： ｃ ＝ ｃ ： ｘ　、ａ ： ｂ ＝ ｂ ： ｙ 　また、ｘ＋ｙ＝ａ　なので、 　ｃ2/ａ ＋ ｂ2/ａ ＝ ａ 　よって、　ａ2＝ｂ2＋ｃ2　が成り立つ。

（コメント）　非常にシンプルな証明ですね！

　上記の証明で、比例式から、

　　　ｂ²＝ａｙ　、　ｃ²＝ａｘ　なので、　ｂ²＋ｃ²＝ａ（ｘ＋ｙ）＝ａ²

とした方がよりシンプルかもしれない。

証明８　　　正方形の分割による証明。（→　参考：「正方形を作る(７)」）

　参考では、格子線に沿った分割であるが、次のような分割を考えてもよい。じっと睨めっこ
すると、３²＋４²＝５² が成り立つことが了解されるだろう。このことを一般化した証明が考え
られる。
　　

（コメント）　これは、証明６を簡略化したものでもある。


（追記）　当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんからピタゴラスの定理の証明を頂
　　　　いた。（平成２７年６月６日付け）

　ピタゴラスの定理には何百という証明方法があるという。（でも知らない。）よくある４つの直
角三角形を組み合わせて、面積の関係から関係式を導き出す方法で理解していたんですが、
こんな証明方法を近頃目にしたのが新鮮だったのでアップしてみます。

証明９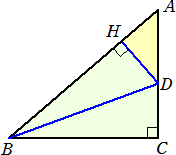	左図の直角三角形ABCで、∠Bの二等分線がACと交わる点 　をD、Dより斜辺ABに下ろした垂線の足をHとすると、 　　△BDH≡△BDCより、　BH=BC=a から、　AH=c-a 　　HD=DC より、AD=b-DC=b-HD 　また、　△BCA∽△DHA から、　(AB+BC)：(AD+DH)=AC：AH

　従って、(c+a)：(b-HD+DH)=b：c-a　より、　(c+a)：b=b：(c-a)　なので、a²+b²=c²　　（証終）


　Dengan kesaktian Indukmu さんからのコメントです。（令和５年４月９日付け）

　ピタゴラスの定理の新証明が面白かったので、ご紹介いたします。

　Here’s How Two New Orleans Teenagers Found a New Proof of the Pythagorean
Theorem | by Keith McNulty | Apr, 2023 | Medium


　うんざりはちべえさんからのコメントです。（令和５年４月９日付け）

　google翻訳しました。

　騒動のもう 1 つの理由は、これらの若い先駆者が提案した証明が、確立された数人の数
学者に彼らの言葉を食い物にするかもしれないということです。

　これは、彼らの証明が三角法を使用しているためです。

　では、なぜそれがそんなに大きな問題なのですか？ さて、私たちの三角恒等式と法則の
多くはピタゴラスの定理に依存しているため、多くの数学者は、三角法を使用した定理の証
明は循環論理であると示唆しています。 別の言い方をすれば、三角法を使用してピタゴラス
を証明することは、基本的に A を使用して B を証明することであり、A が既に B に依存して
いる場合に、彼らは主張します。定理の三角法による証明、および三角法の証明は不可能
であることを明示的に述べています。

　しかし、この観点はここ数十年でますます疑問視されてきており、それ以来、ピタゴラスの
いくつかの三角法による証明が行われてきました。ジョンソンとジャクソンの証明がピタゴラ
スの最初の三角法による証明であるというメディアの主張は誇張されていますが、彼らの証
明は、これまでに見た中で最も美しく、最も単純な三角法の証明である可能性が十分にあり、
明らかに若くて鋭い知性の作品であり、 多くの経験豊富な数学者の仕事を特徴付ける深い
研究の年。

　新しい手法なんだけど、要するに、

　別の言い方をすれば、三角法を使用してピタゴラスを証明することは、基本的に A を使用
して B を証明することであり、A が既に B に依存している場合に、彼らは主張します。定理
の三角法による証明、および三角法の証明は不可能であることを明示的に述べています。

ということが、問題点でもあるということですね。


　Dengan kesaktian Indukmu さんからのコメントです。（令和５年４月１０日付け）

　はい。ですので、今回はそうした循環論法を避けている、という理解でよろしいことかと。


　DD++ さんからのコメントです。（令和５年４月１０日付け）

　いえ、よーーーく読むと循環論法の完全な回避は微妙に失敗してます。

　In this case we have an isoceles right-angled triangle and, our angles α = β = π/4 radians.
So our hypotenuse is a/sin(π/4) = √2a, which satisfies the Pythagorean Theorem.

　その sin(π/4) の値はどこから？通常は三平方の定理で導出するものでしょうから、循環
論法を避けることに成功したと主張するには、これを別の方法で導出して見せる必要があっ
たでしょう。

　まあ、相似な図形の面積比を使うとか回避方法はいくらでもあるので、加筆修正は容易で
しょうけど。


　Dengan kesaktian Indukmu さんからのコメントです。（令和５年４月１０日付け）

　おおっ。a=b の特殊なケースでは、AやCの分母が 0 になってしまい、今回の証明が通用
しない、そういう話の流れなのですね！！

　そのケースでの短証明に、sin(π/4) を使うのは確かに反則ですね。

　寄せられていたコメントを追いかけたところ、a = b のケースでは、次のように改善する案が
あげられていました。

　By the way, that case is trivial: the triangle is a one-fourth of a square whose side length
is $c$. The area of this square is c^2, while the triangle’s area is (ab)/2 = a^2/2. Therefore
c^2=4 times a^2/2 = 2a^2 = a^2+b^2, as desired.


　うんざりはちべえさんからのコメントです。（令和５年４月１０日付け）

　google翻訳しました

　この新しい証拠は何ですか？

　わかりましたので、これが私が考える方法です。 この図を見て、この証明を通してずっと参
照してください。図のように、辺 a、b、c (斜辺) を持つ左上の単純な直角三角形から始めま
しょう。 ここでは、a ≠ b と仮定しましょう。この記事の最後の注で、a = b の自明な特殊な
ケースを扱います。 長さ b と c の辺の間の角度をαとし、長さ a と c の辺の間の角度を
β とします。 次に、この元の直角三角形から 3 つの幾何学的なステップを作成します。

長さ b の辺に反映して、右上の等価三角形を形成します。
元の三角形の長さ c の辺に垂直な直線を延長します。
反射した三角形の斜辺から連続線を延長します。

ステップ 2 と 3 から延長した線が交わると、図のように、斜辺の長さが C、辺が A と c の新
しい大きな直角三角形が形成されます。

　この大きな直角三角形内に、図のように一連の小さくて小さい類似の直角三角形を描画
し、サイズが減少する類似の三角形の無限のシーケンスを形成します。

　この無限の相似三角形のシーケンスを使用して、長さ A と C を導出する方法を調べます。

　小さい三角形の辺の長さを導き出す

　辺の長さ A の左上から 1 番目の直角三角形を見ると、この三角形の辺の長さは 2a であ
り、したがって、斜辺の長さは 2a/sinβ です。 しかし、元の三角形から、sinβ = b/c である
ことがわかっているので、この斜辺は長さ (2ac)/b であると結論付けることができます。
これにより、この三角形の 3 番目の辺は 2a²/b になります。

　すぐに右側の三角形に移動すると、短辺の 1 つが長さ 2a²/b であることがわかります。
したがって、この三角形の斜辺 (辺の長さ C のセグメント) は 2a²/(bsinβ) = (2a²c) /b²
です。

　このプロセスを続けることができますが、小さな相似三角形のそれぞれが a²/b² の係数
で減少することが明らかになります。 これは、長さ A が最初の項 (2ac)/b と公比 a²/b² を
持つ等比級数であることを意味します。 同様に、長さ C は c で始まり、最初の項 (2a²c)/b²
と公比 a²/b² の等比級数になります。

長さ A と C の計算

　これで、等比級数の和の式を使用して、長さ A と C を計算できます。初項 k と公比 r の
等比級数の和の式は、k/(1-r) です。 この合計は、r の絶対値が 1 未満の場合に収束しま
す。この場合、r は a²/b² であるため、常に収束することを確認できます (a＞b の場合は、
それらを交換するだけです)。

　それでは、長さ A を計算してみましょう。この場合、k = (2ac)/b および r = a²/b² となるの
で、A=2ac/b(1-a^2/b^2)=2abc/b^2-a^2　、k = (2a²c)/b² で同様のアプローチを使用し、最
初に c を追加する必要があることを思い出してください。

　C=c+2a^2c/b^2(1-a^2/b^2)=c(b^2+a^2)/(b^2-a^2)

それでは、長さ A を計算してみましょう。この場合、k = (2ac)/b および r = a²/b² となるので、
k = (2a²c)/b² で同様のアプローチを使用し、最初に c を追加する必要があることを思い出
してください。

　この美しい証明を締めくくる

　A と C の比を取るとどうなるか見てみましょう。　A/C=2ab/(a^2+b^2)
しかし、元の図から、これは sin(2α) であることがわかります。

　ここで、元の直角三角形を反映して形成された上の二等辺三角形の正弦規則を見てみま
しょう。 正弦定理は直角三角形に依存しないことに注意してください。 サイン ルールは、ど
の三角形でも、辺とその反対側の角度のサインとの比率は常に同じであると述べています。

　したがって、sin 2α/2a=sinβ/c

　したがって、現在わかっていることを次の式に変換します。　b/(a^2+b^2)=b/c^2

　この状況では、a、b、c のいずれもゼロではないことに注意し、分子が同一であることに注
意すると、分母が同一であるという結論に至ります。 これでピタゴラスの定理が証明されまし
た。

[注] a = b という特殊なケースでは、三角形に長さ a の 2 つの短い辺と斜辺がある場合、証
明は自明です。 この場合、直角二等辺三角形があり、角度 ? = β = π/4 ラジアンです。
したがって、斜辺は a/sin(π/4) = √2a であり、ピタゴラスの定理を満たします。
ミディアムユーザーに感謝　ウォットシット　この特別なケースに対処する必要性を指摘して
くれて。


（コメント）　アメリカの２人の十代の少女 Calcea Johnson さんと Ne’Kiya Jackson さんに
　　　　　　よってなされた証明を追認してみました。

　三角比の定義のみを用いていれば、ｓｉｎ²θ＋ｃｏｓ²θ＝１ という性質に依存しない限り
循環論法にはならないということを確認し、新たなピタゴラスの定理の証明を拝見したいと
思います。

　直角三角形の底辺の長さを ａ、高さを ｂ とし、斜辺の長さを ｃ とおき、さらに、ここでは、
ａ＜ｂ と仮定します。

　次のように、順次相似な直角三角形を連結していく。



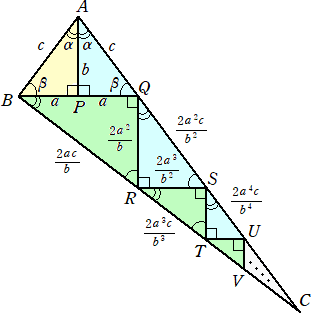
　このとき、無限等比級数の和を計算して、

　ＢＣ＝２ａｂｃ/（ｂ²−ａ²）　、ＣＡ＝ｃ（ａ²＋ｂ²）/（ｂ²−ａ²）

なので、　ｓｉｎ２α＝２ａｂ/（ａ²＋ｂ²）

　ここで、△ＡＢＱにおいて、正弦定理より、　２ａ/ｓｉｎ２α＝ｃ/ｓｉｎβ　なので、

　（ａ²＋ｂ²）/ｂ＝ｃ/（ｂ/ｃ）＝ｃ²/ｂ　より、　ａ²＋ｂ²＝ｃ²　が成り立つ。


（コメント）　正弦定理は余弦定理から導かれ、余弦定理は、ほぼピタゴラスの定理なので、
　　　　　　循環論法を回避しているかどうかは疑問です．．．。


　Dengan kesaktian Indukmu さんからのコメントです。（令和５年４月１０日付け）

　拾いものです。

　cos ｙ ＝ｃｏｓ（ｘ−（ｘ−ｙ））＝ｃｏｓ ｘ ｃｏｓ（ｘ−ｙ）＋ｓｉｎ ｘ ｓｉｎ（ｘ−ｙ）

＝ｃｏｓ ｘ （ｃｏｓ ｘ ｃｏｓ ｙ ＋ｓｉｎ ｘ ｓｉｎ ｙ）＋ｓｉｎ ｘ （ｓｉｎ ｘ ｃｏｓ ｙ −ｃｏｓ ｘ ｓｉｎ ｙ ）

＝（ｃｏｓ²ｘ＋ｓｉｎ²ｘ）ｃｏｓ ｙ

　cos y が 0 でなければ、両辺をこれで割る。

　以上は、ピタゴラスの定理を陽には使わずに、cos^2x ＋sin^2x ＝ 1 を示すものです。


　DD++ さんからのコメントです。（令和５年４月１０日付け）

　加法定理は一体どこから湧いて出たのでしょうか。sin や cos を微分で定義している場合
は加法定理もマクローリン展開と二項定理で示すことになるでしょうし、その場合はこれで
大丈夫という話なのかな？

．．．と思いましたが、少し考えてみたら、

　s’(x) = c(x)　、c’(x) = -s(x)　、s(0) = 0　、c(0) = 1

の解を s(x) = sin x、c(x) = cos x とする定義の場合、

{ (sin x)^2 + (cos x)^2 }’ = 0 が一瞬で示せるので、加法定理を使うまでもなかった……。

　級数で定義した場合も、この微分の関係式をすぐ作れますし、何を目的とした式変形だっ
たんでしょうねコレ。


　Dengan kesaktian Indukmu さんからのコメントです。（令和５年４月１０日付け）

　失礼しました。拾った場所を記し漏らしました。こちらです。


　DD++ さんからのコメントです。（令和５年４月１０日付け）

　あ、鋭角限定なんですね。それなら確かに加法定理に三平方は不要ですね。

　でも、鋭角限定でもやっぱり加法定理使うまでもないような気もしますね。

　∠B = θ、∠C = π/2、AB = 1 の三角比の定義に使ういつもの直角三角形 ABC に対し、

辺 DE が点 C を通るように長方形 ABDE を書けば、相似な直角三角形が 3 つできて、

　BC = cosθ で、DC = (cosθ)^2

　AC = sinθ で、EC = (sinθ)^2

より、　(cosθ)^2 + (sinθ)^2 = DC + EC = AB = 1　で終わる話なような。


　うんざりはちべえさんからのコメントです。（令和５年４月１１日付け）

　ですので今回はそうした循環論法を避けている、という理解でよろしいことかと。

　しかし、sinα、sinβという三角関数の概念を使っていますよね。

　辺の長さ A の左上から 1 番目の直角三角形を見ると、この三角形の辺の長さは 2a であ
り、したがって斜辺の長さは 2a/sinβ です。 しかし、元の三角形から、sinβ = b/c であるこ
とがわかっているので、この斜辺は長さ (2ac)/b であると結論付けることができます。 これに
より、この三角形の 3 番目の辺は 2a²/b になります。

より、明らかですね。sinβ = b/c は、

　すぐに右側の三角形に移動すると、短辺の 1 つが長さ 2a²/b であることがわかります。し
たがって、この三角形の斜辺 (辺の長さ C のセグメント) は 2a²/(bsinβ) = (2a²c) /b² です。

でも使われています。b/c をsinβということなしに、論理はくみたてられないと思います。

　A と C の比を取るとどうなるか見てみましょう。A/C=2ab/(a^2+b^2)　しかし、元の図から、
これは sin(2α) であることがわかります。

　ここでも、sin(2α)という三角関数の概念が使われています。

　循環論法を避けている

とは言えないのではないでしょうか？でなければ、文章の前半は、いらなかったはずです。
「循環論法なるけど、」という前置きがあるから、この文書があるのではないでしょうか？


　DD++ さんからのコメントです。（令和５年４月１１日付け）

　三角関数の定義自体を使うだけなら循環論法にはなりませんよ。お手元の数学の教科書
を見てください。

　(sinθ)^2 + (cosθ)^2 = 1 という重要な式の証明に、三平方の定理が関わっていますね。

だから、そのページより後に書いてあることは、三平方の定理の証明に使ってはなりません。

言い方を変えれば、そのページより前に書いてあることは別に使っても何も問題はないんです。

だから「三角関数（の三平方の定理を使う前の部分）できちんと三平方の定理を証明すること
に成功した」という話題なのですよ。

　はちべえさんはどうも数式しか見ていないようですが、言語と合わせて読むようにした方が
よろしいかと。


　Dengan kesaktian Indukmu さんからのコメントです。（令和５年４月１１日付け）

　(sinθ)^2 + (cosθ)^2 = 1　を前提とせずに、正弦定理ってなりたつんだっけ？くらいを念の
ために確認はいたしました。循環論法になっていないことを確認するためです。


　DD++ さんからのコメントです。（令和５年４月１１日付け）

　あ、そういえば正弦定理使ってましたか。では、前回のコメントを訂正。

　「三角関数（の三平方の定理を使う前の部分と、教科書の掲載順的には後ろだけど三平
方を使うものに依存せず証明が構成されているもの）できちんと三平方の定理を証明する
ことに成功した」

ですね。

　鋭角の三角比の定義
　tan = sin / cos
　鋭角の正弦定理
　第一余弦定理（高校で習うやつは第二余弦定理で、そっちはダメ）
　鋭角の加法定理……くらいですか。

　なんか昔、似たようなことやったような、と思って調べてみたら、ありました。

　「中線定理」　・・・　三平方の定理を使わずに中線定理を示せるか、という話題です。


　Dengan kesaktian Indukmu さんからのコメントです。（令和５年４月１３日付け）

　上記の（コメント）から、疑義があがっていることに気が付きました。概ね、下記のごとくと
存じます。

　「正弦定理は(第２)余弦定理から導かれる。この余弦定理からは直接に三平方の定理が
導かれる。ジョンソンとジャクソンによる今回の新証明が正弦定理に依拠するのはまずいの
ではないか？」

　私も少々考え込みました。調べたところ、以下もわかりました。すなわち

　三角関数の加法定理のもとでは、正弦定理と第１・第２余弦定理は同値である。

　ですから、加法定理に依拠しつつ、ジョンソンとジャクソンとの新証明を理解すること、これ
はまずかろう。循環論法の謗りを免れない。じゃあ、どうすればいいのか？

　正弦定理の各種の証明を調べてくださっているテキストをみつけました。

　上記のなかから適切なものを見いだせればよいと思いました。

　ジョンソンとジャクソンは、面積による証明を回避し、辺の長さの相似を利用していますか
ら、その志向とも整合したほうが良いですね。

　さきの文書の「普通の証明（２）」が解りやすいかと思いました。

あるいは、

　「９　幾何学的証明　ヨーロッパにおける三角法の基礎をつくったﾚｷﾞｵﾓﾝﾀﾇｽ(1436-1376)
の証明」

も素敵です。それにしても、DD++さんによる

　でも、鋭角限定でもやっぱり加法定理使うまでもないような気もしますね。

　∠B = θ、∠C = π/2、AB = 1 の三角比の定義に使ういつもの直角三角形 ABC に対し、

辺 DE が点 C を通るように長方形 ABDE を書けば、相似な直角三角形が 3 つできて、

　BC = cosθ で、DC = (cosθ)^2

　AC = sinθ で、EC = (sinθ)^2

より、　(cosθ)^2 + (sinθ)^2 = DC + EC = AB = 1　で終わる話なような。

は、クールですね。


　DD++ さんからのコメントです。（令和５年４月１３日付け）

　手元に高校数学の教科書がないので記憶頼りですが、日本の高校教育では、正弦定理
は同じ円周角をもつ直角三角形を使って証明していたと思います。

　そこで使っているのは、

・円周角の定理
・タレスの定理
・三角比の定義
・直径と半径の定義

くらいだったはずで、三平方の定理は全く使ってないですね。

　余弦定理を使う方法は、私は今回調べて初めて存在を知りました。海外だと、どの方法で
の証明がメジャーなんだろう。

　law of sines で検索して英語ページをいろいろ見てみました。

　日本とは違って、「=2R」 がついていない形で紹介されていることがほとんどのようです。
そのため、証明も以下で終わりというのが普通のよう。

　A も B も鋭角の場合、頂点 C から辺 AB に下ろした垂線の長さを考えると、

　b*sinA = a*sinB

　両辺を sinA および sinB で割って、正弦定理が得られる。

　どちらかが鈍角の場合は、内角と外角の正弦の値は等しいことを考えれば同じことが言
える。

　問題は、三平方の定理を使っているかどうか。

　直角や鈍角の場合は、そもそも三平方の定理を使って定義するのでダメですが、鋭角の
場合に限定すれば、使ってないですね。そして、件の証明では、2αもβも鋭角です。

　よって、海外で主流っぽい正弦定理の証明方法を前提とした場合、循環論法にはなって
いないと言ってよさそうです。


（コメント）　DD++ さん、探究ありがとうございます。循環論法にはならないとの由、安心しま
　　　　　　した！



　　以下、工事中！