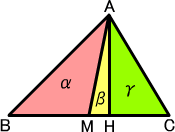
パーツα:△ABM と合同な鈍角三角形
パーツβ:△AMH と合同な直角三角形
パーツγ:△AHC と合同な直角三角形
パーツε:平行辺が HC と AH+HC、脚が MH と AM である直角台形
AB≠AC である△ABCにおいて、辺BCの中点をMとするとき、
中線定理 AB2+AC2=2(AM2+BM2)
を証明せよ。ただし、三平方の定理を用いないものとする。
(AB=AC の場合は三平方の定理そのものなので除外)
(コメント) 「三平方の定理」をどの範囲まで許容していいのか疑問ですが、すぐ思いつく証
明は、ベクトルを利用するものではないでしょうか?
△ABCの辺BCの中点をMとし、ベクトルMA=a、MB=b とおくと、
AB2+AC2=|a−b|2+|a+b|2=2(|a|2+|b|2)=2(AM2+BM2)
DD++さんからのコメントです。(平成27年12月15日付け)
箱詰めパズルで強引になんとかしました。
[証明] B<C として一般性を失わない。まずは、C<π/2 の場合を考える。
点Aから線分MCに垂線AHを下ろす。以下のように図形を命名しておく。
 |
パーツα:△ABM と合同な鈍角三角形 パーツβ:△AMH と合同な直角三角形 パーツγ:△AHC と合同な直角三角形 |
| パーツδ:底辺が 2MH で等辺が AM である二等辺三角形 パーツε:平行辺が HC と AH+HC、脚が MH と AM である直角台形 |
|
大長方形:辺長が AH+BH と 2AH+BC の長方形
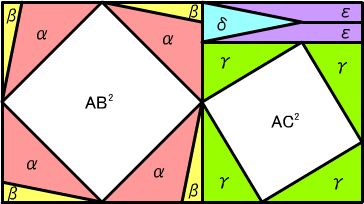
αを4つ、βを4つ、γを4つ、δを1つ、εを2つ、の15パーツのセットを補助パーツセットと
呼ぶことにする。
まず、辺長 AB の正方形、辺長 AC の正方形、補助パーツセット、で大長方形を隙間も重
なりもなく構成することができることを示す。
αの AM 部分をβの斜辺にくっつけた直角三角形を4組用意する。それを辺長 AB の正
方形の各辺にくっつけると辺長 AH+BH の正方形ができる。
一方で、辺長 AC の正方形の各辺にγをくっつけると辺長 AH+HC の正方形になる。
そこに、δ2つとεを組み合わせてできる辺長 2MH と AH+HC の長方形をくっつけると、
片方の辺長が AH+HC+2MH=AH+MC+MH=AH+BM+MH=AH+BH の長方形になるので、
これを最初の正方形とくっつけると新しくできた辺長は (AH+BH)+(AH+HC)=2AH+BC となり、
ぴったり上図の大長方形となる。
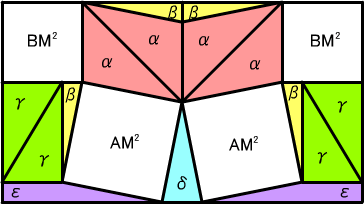
次に、辺長 AM の正方形2つ、辺長 BM の正方形2つ、補助パーツセット、でも大長方形
を隙間も重なりもなく構成することができることを示す。
εの AH+HC 部分、δの 2MH 部分、εの AH+HC 部分、をこの順に一直線に並べる(た
だしεはそれぞれ直角を外側にする)。
このとき、合計の長さは (AH+HC)+2MH+(AH+HC)=2AH+2MC=2AH+BC で大長方形の長
辺に等しい。
このδとεのそれぞれの AM 部分を共有するように辺長 AM の正方形を置く。
(εが対称に2つあるので、正方形も対称に2つ置ける。以下でも同様に対称に2つずつ置い
ていく)
γの斜辺同士をくっつけた長方形を作り、εの HC 部分にくっつける。
置いた長方形と正方形の間にβがぴったり当てはまる。
βの底辺とγの底辺がつながってできた長さ BM の辺に辺長 BM の正方形をくっつける。
このとき、εとγと正方形が作るまっすぐな辺の長さは MH+AH+BM=AH+BH で大長方形
の短辺に等しい。
辺長 AM の正方形と辺長 BM の正方形が角を共有しているところに両方と辺を共有する
ようにαを置く。さらに、そのαと合わせて平行四辺形になるようにもう1つαを置く。
最後に残った凹んだ部分にはβがちょうど当てはまり、ぴったり上図の大長方形となる。
以上の2つより、「辺長 AB の正方形、辺長 AC の正方形、補助パーツセット」の面積合計
と「辺長 AM の正方形2つ、辺長 BM の正方形2つ、補助パーツセット」の面積合計は等しい
ことがわかる。
補助パーツセットは全く同一内容の並べ替えなので両方から取り除くと、前者の2つの正
方形の面積合計と後者の4つの正方形の面積合計は等しい、
すなわち、 AB2+AC2=2(AM2+BM2)
C≧π/2 の場合は、中線 AM で △ABM と △A'MCにわけ、片方を M を中心に半回転さ
せて B と C が重なるようにくっつけ直すと、AM=A'M と ∠BAM<∠CA'M<π/2
から、
BA2+CA2=2(BM2+AM2) すなわち、 AB2+AC2=2(AM2+BM2) [証終]
#実際の図がないと、なかなかわかりづらいですかね。なんにせよ、三平方の定理なしでは
こんな感じの図形組換え的証明法が唯一なのではと思います。長さの二乗を作る方法が、
正方形の面積くらいしかなさそうですし。方ベキの定理(接線時)もありますが、役に立たなさ
そうですしね。
(コメント) 平成27年12月20日付けで、DD++さんより上記の図をメールでいただきました。
説明文が分かりやすくなりました。DD++さんに感謝します。
DSさんからのコメントです。(平成27年12月16日付け)
自分は三平方の定理自体が等積変形と回転移動で証明できるのでそれを参考にして考
えました。やっていることはDD++さんと同じく面積のきりわけと移動ですが、計算自体にあ
まり頼らないので、イメージするのは幾分楽かと思います。
(もっといい方法があるかもしれません)
概要だけ言うとこんな感じです。
△ABCの辺AB、ACの中点をそれぞれM、Nとします。また、AB、ACと同じ長さの辺の正方
形をそれぞれが一辺を共有するようにして△ABCの外側に作り、それぞれの正方形の中心
をP、Qとします。同じようにして、MNを一辺とする正方形をA側に作り、その中心をRとします。
このとき、「PRQは一直線上かつPR=QR」・・・(*) をまず証明します。
次に、中線定理の式 AB2+AC2=2(AM2+BM2) はBCに関してAと反対側にA'を四角
形ABA'Cが平行になるように取り、またその平行四辺形の各辺の中点を結んだ平行四辺形
を作ると、
(大きい平行四辺形の外側に直角二等辺三角形4つを斜辺で貼り合わせたもの)
=(小さい平行四辺形に外側に直角二等辺三角形4つを斜辺で貼り合わせたもの)×2・・・(**)
を意味することがわかります。最後に、
平行四辺形に直角二等辺三角形4つを斜辺で貼り合わせたものの面積は各直角二等辺
三角形の直角をなす点を結んだ図形の面積に等しくなる・・・(***)
ことを証明します。(*)、(**)、(***)より中線定理が示されます。
図的には正方形の中に各中点を結んだ正方形が出来ることになります。やっていることは
一回切り分けて回転移動させて(**)の両辺をそれぞれ正方形にするということだけです。
記号が多いとごちゃごちゃなるのであえてこれくらいで書いています。
DD++さんからのコメントです。(平成27年12月16日付け)
(**)以降の流れは理解できましたが、(*)のRが線分PQの中点になる証明だけ、どのように
すればよいのかわかりませんでした。合同になりそうな三角形はいくつかある気配ですが、ど
のようにするのでしょう?
予想外の方法がありました。三平方の定理禁止という条件下ではおそらくこれが一番わかり
やすいでしょう。
[証明] B<C として一般性を失わない。まずは、C<π/2 の場合を考える。
(cos の鈍角拡張は三平方の定理を前提としているためこの仮定が必要)
点Aから辺 BC に垂線を下ろして考えると、BC = AB cos∠B + AC cos∠C
両辺に BM をかけて、BC=2BM に気をつけると、
2BM2 = AB BM cos∠B + AC BM cos∠C ……(1)
点Bから中線 AM の延長に垂線を下ろして考えると、
AM = AB cos∠BAM - BM cos∠AMC
両辺に AM をかけると、
AM2 = AB AM cos∠BAM - AM BM cos∠AMC ……(2)
点Cから中線 AM に垂線を下ろして考えると、 AM = AC cos∠CAM + CM cos∠AMC
両辺に AM をかけると、 AM2 = AC AM cos∠CAM + AM CM cos∠AMC ……(3)
点Mから辺 AB に垂線を下ろして考えると、 AB = AM cos∠BAM + BM cos∠B
両辺に -AB をかけると、 -AB2 = - AB AM cos∠BAM - AB BM cos∠B ……(4)
点Mから辺 AC に垂線を下ろして考えると、 AC = AM cos∠CAM + CM cos∠C
両辺に -AC をかけると、 -AC2 = - AC AM cos∠CAM - AC CM cos∠C ……(5)
BM=CM に気をつけて5つの式を全て足すと、 2BM2 + 2AM2 - AB2 - AC2 = 0
すなわち、 AB2+AC2=2(AM2+BM2)
C≧π/2 の場合は、先の証明のように半分を半回転して示される。 [証終]
#第一余弦定理は三平方の定理を必要とせず、また三角比の公式が全滅でも同一項の減
算でcosを消し去るには何の影響もなかったというオチ。
DSさんからのコメントです。(平成27年12月16日付け)
成る程…そういう抜け道がありましたか。面積移動以外の道を閉ざしたつもりでしたがどう
やら考えが足りていなかったようです。ありがとうございました。
キエペルトの定理も三角関数の定義のみで証明できることをふと思い出しました。
(*)の証明はこんな感じです。
Mからまた、Nから下ろした垂線の足をそれぞれM'、N'として、直角三角形MM'B、NN'Cを
それぞれM、Nを中心としてMM'、NN'が直線MNと重なるようにかつAとMNに関して同じ側に
来るように90度回転すると、B、CはそれぞれP、Qに一致します。
また、RからMNに下ろした垂線の足をR'とします。このとき、
MR'=NR'⇔MM'+MR'=NR+NN'・・・(a) 、MN=BM'+CN'・・・(b)
(a)、(b)より題意が示されます。
#図的には長方形の中心を通る直線でその長方形を切り落とした感じになります。
DD++さんからのコメントです。(平成27年12月16日付け)
Mからまた、Nから下ろした垂線の足をそれぞれM'、N'として
辺BCまたはその延長上への垂線ということでいいんでしょうか?
MR'=NR'⇔MM'+MR'=NR'+NN'・・・(a) 、MN=BM'+CN'・・・(b)
BやCが鈍角の場合は(b)は成立しないと思います。
DSさんからのコメントです。(平成27年12月16日付け)
その通りですね。図形でやるので場合わけが必要ですね。その場合は鈍角側は△ABCの
外側に片方の直角三角形が来ることになりますね。それを90度回転すると同じ結果が得られ
ると思います。
DD++さんからのコメントです。(平成27年12月16日付け)
外側に来るので、回転でMNを挟んでAと反対側に来て、「長方形を半分に切ったような形
だから明らか」とはできない形になります。結果は同じでしょうけど、同じ道ではたどり着けま
せん。一直線上にある保証さえできればあとは三角形の相似でなんとでもなりそうですが、
一直線上にある証明はなかなか大変そうですよ。
Cが直角の場合については、R'が中線の中点であることを示せばいけそうですかね。
(閑話休題) ベクトルの内積の展開公式って証明に三平方の定理使わないんですね。てっ
きり使ってるものだと思って候補から除外してました……。
ところで、私の図形組換え式証明の図ってこちらで作ってメールでお送りするかなにかした
方がいいですかね?(よろしくお願いします...<(_ _)>)
第一余弦定理やベクトルでの証明が出てきた今、もうあんまり価値のない証明になってま
すが。
DSさんからのコメントです。(平成27年12月17日付け)
(b)の左辺の片方がマイナスになるというだけです。MNを縦の長さに持つ長方形をその中
心がRになるように、そして縦の辺がMNと垂直になるように補助的に導入すると、それほど
やっていることは変わらないということがわかると思います。
DD++さんからのコメントです。(平成27年12月17日付け)
あれ?私が思ってた「長方形」と全然違った……。
(コメント) 第2余弦定理も、距離の公式を用いて示す方法と第1余弦定理を用いて示す方
法がありますが、次のような証明はありでしょうか?距離の公式を援用しているっ
ぽい感じがするのですが...。距離の公式やsin2θ+cos2θ=1などの公式は
三平方の定理そのものですよね!
「適切な座標系」において、示されていることであるが...。
△AMBにおいて、 cos∠AMB=(AM2+BM2−AB2)/(2AM・BM)
△AMCにおいて、 cos∠AMC=(AM2+BM2−AC2)/(2AM・BM) (← BM=CM)
ここで、 cos∠AMC=cos(180°−∠AMB)=−cos∠AMB より、
AM2+BM2−AC2=−(AM2+BM2−AB2)
すなわち、 AB2+AC2=2(AM2+BM2)
フォン・ノイマンやパスクアル・ヨルダンによって、「中線定理の成立」と「ノルムの存在」が
同義であることが示されている。(1935年)
このことから、三平方の定理は距離(ノルム)そのもので、三平方の呪縛なしに中線定理を
示すことは不可能であるように感じる。
