スチュワートの定理　　　　　　　　　　　　　　　　　　　　　　　　　

　初等幾何でよく使われる定理と言えば、ピタゴラスの定理に並んで中線定理だろう。

中線定理　・・・　△ＡＢＣにおいて、辺ＢＣの中点をＭとする。このとき、

　　　　　　　　　　　　　　　ＡＢ²＋ＡＣ²＝２（ＡＭ²＋ＢＭ²）

　（証明は、「適切な座標系」を参照）

　この中線定理では、「辺ＢＣの中点をＭ」という非常に窮屈な形になっていると日頃より気
になっていた。

　中線定理を次のように拡張した定理があることを知り、ようやく安堵した次第である。

定理（Stewart）

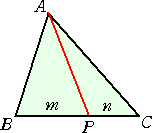
△ＡＢＣにおいて、辺ＢＣを ｍ ： ｎ に内分する点を Ｐ とする。 このとき、 　　 が成り立つ。

　上記の公式で、 ｍ＝ｎ の場合が中線定理である。


　通常、スチュアートの定理は、

　　　　ｎ・ＡＢ²＋ｍ・ＡＣ²＝（ｍ＋ｎ）・ＡＰ²＋ｎ・ＢＰ²＋ｍ・ＣＰ²

の形で世に知られているようだ。上記の式では覚えにくいので、分点の公式になぞらえて
定理のような形に変形した。

（証明）　Ａ（ａ，ｂ）、Ｂ（−ｍｋ，０）、Ｃ（ｎｋ，０）、Ｐ（０，０）　と座標を定める。（ ｋ は比例定数）

　このとき、　ＡＢ²＝（ａ＋ｍｋ）²＋ｂ²　、　ＡＣ²＝（ａ−ｎｋ）²＋ｂ²

　　　　　　　　ＢＰ²＝ｍ²ｋ²　、　ＣＰ²＝ｎ²ｋ²

なので、　　ｎ・ＡＢ²＋ｍ・ＡＣ²−ｎ・ＢＰ²−ｍ・ＣＰ²

　　　　　　＝ｎ・｛（ａ＋ｍｋ）²＋ｂ²｝＋ｍ｛（ａ−ｎｋ）²＋ｂ²｝−ｎ・ｍ²ｋ²−ｍ・ｎ²ｋ²

　　　　　　＝（ｍ＋ｎ）（ａ²＋ｂ²）

　　　　　　＝（ｍ＋ｎ）ＡＰ²

　よって、　ｎ・ＡＢ²＋ｍ・ＡＣ²＝（ｍ＋ｎ）ＡＰ²＋ｎ・ＢＰ²＋ｍ・ＣＰ²　が成り立つ。　（証終）

　上記では座標幾何により証明したが、余弦定理を用いても証明される。

（別証）　△ＡＢＰと△ＡＣＰにおいて、余弦定理より、 　　　　　　　ＡＢ2＝ＡＰ2＋ＢＰ2−２ＡＰ・ＢＰ・cos∠ＡＰＢ 　　　　　　　ＡＣ2＝ＡＰ2＋ＣＰ2−２ＡＰ・ＣＰ・cos∠ＡＰＣ 　　　　　cos∠ＡＰＢ＝−cos∠ＡＰＣ　で、ｎ・ＢＰ＝ｍ・ＣＰ　より

ｎ・ＡＢ²＋ｍ・ＡＣ²＝ｎ・（ＡＰ²＋ＢＰ²−２ＡＰ・ＢＰ・cos∠ＡＰＢ）
　　　　　　　　　　　　　　　　　　　　　　　＋ｍ・（ＡＰ²＋ＣＰ²−２ＡＰ・ＣＰ・cos∠ＡＰＣ）

　　　　　　　　　　　＝ｎ・（ＡＰ²＋ＢＰ²）＋２ＡＰ・ｎ・ＢＰ・cos∠ＡＰＣ）
　　　　　　　　　　　　　　　　　　　　　　　＋ｍ・（ＡＰ²＋ＣＰ²）−２ＡＰ・ｍ・ＣＰ・cos∠ＡＰＣ）

　　　　　　　　　　　＝ｎ・（ＡＰ²＋ＢＰ²）＋２ＡＰ・ｍ・ＣＰ・cos∠ＡＰＣ）
　　　　　　　　　　　　　　　　　　　　　　　＋ｍ・（ＡＰ²＋ＣＰ²）−２ＡＰ・ｍ・ＣＰ・cos∠ＡＰＣ）

　　　　　　　　　　　＝ｎ・（ＡＰ²＋ＢＰ²）＋ｍ・（ＡＰ²＋ＣＰ²）

　　　　　　　　　　　＝（ｍ＋ｎ）ＡＰ²＋ｎ・ＢＰ²＋ｍ・ＣＰ²　　（別証終）

（コメント）　どちらの証明がより簡単か、いろいろ意見の分かれるところだろう．．．。