
仭丂惓幩塭偵偮偄偰
丂嬻娫恾宍偼幚暔偦偺傕偺傪巻柺偵昤偗側偄偙偲傕偁偭偰丄堦斒揑偵棟夝偟偯傜偄偙偲偑懡
偄丅偦偙偱丄惓幩塭傪峫偊傞偙偲偵傛偭偰丄嬻娫恾宍傪攃埇偟偰傒傛偆丅惓幩塭偼奣擮偲偟偰
偼扨弮偱偁傞偑丄惓幩塭屌桳偺惈幙偑柺敀偄丅
惓幩塭丒嬻娫偺昁恵庤朄丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
仭丂惓幩塭偵偮偄偰
丂嬻娫恾宍偼幚暔偦偺傕偺傪巻柺偵昤偗側偄偙偲傕偁偭偰丄堦斒揑偵棟夝偟偯傜偄偙偲偑懡
偄丅偦偙偱丄惓幩塭傪峫偊傞偙偲偵傛偭偰丄嬻娫恾宍傪攃埇偟偰傒傛偆丅惓幩塭偼奣擮偲偟偰
偼扨弮偱偁傞偑丄惓幩塭屌桳偺惈幙偑柺敀偄丅
| 惓幩塭偺掕媊 | |
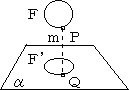 |
丂恾宍俥偺擟堄偺揰傪俹偲偡傞丅揰俹傪捠傝丄暯柺兛偵悅捈側捈慄倣傪 堷偒丄倣偲兛偲偺岎揰傪俻偲偡傞丅揰俹偑恾宍俥慡懱傪摦偔偲偒偵揰俻偑 摦偄偰弌棃傞暯柺兛忋偺恾宍傪俥乫偲偡傞丅 丂丂偙偺偲偒丄乽恾宍俥傪暯柺兛偵惓幩塭偟偨恾宍偑俥乫偱偁傞乿偲偄偆丅 |
楙廗侾乮揰偺惓幩塭乯丂揰俹乮俁丆俈丆亅侾乯偺暯柺兛丗倶亅俀倷亄倸亖侽 忋傊偺惓幩塭傪媮傔傛丅
乮摎乯丂乮俆丆俁丆侾乯
楙廗俀乮捈慄偺惓幩塭乯丂捈慄倣丗倶亖倷亅侾亖俀亅俀倸 偺暯柺兛丗倶亅俀倷亄倸亖侽 忋傊偺惓幩
丂丂丂塭傪媮傔傛丅
乮摎乯丂乮倶亅俇乯/俆亖乮倷亅俁乯/俀亖亅倸
楙廗俁乮儀僋僩儖偺惓幩塭乯丂倎偺倐忋傊偺惓幩塭傪媮傔傛丅
乮摎乯丂乮倎丒倐乯倐/乥倐乥2
丂楙廗俁偺墳梡偲偟偰丄師偺栤偼懄摎偱偒傞偩傠偆丅
楙廗係丂媴柺俽丗乮倶亅侾乯2亄倷2亄乮倸亄侾乯2亖俁俇 偺拞怱傪俠偲偡傞丅揰俙傪俽忋偺侾揰偲偡傞
丂丂丂偲偒丄俙偵偍偗傞俽偺愙暯柺忋偵擟堄偺揰俹傪偲傞丅偙偺偲偒丄撪愊俠俹丒俠俙傪媮傔傛丅
乮摎乯丂俁俇
楙廗俆丂摨堦捈慄忋偵側偄俁揰俙丄俛丄俠偵偮偄偰丄捈慄俙俠偵娭偟偰儀僋僩儖俙俛偲懳徧側儀
丂丂丂僋僩儖傪丄俙俛丄俙俠傪梡偄偰昞偣丅
乮摎乯丂俀乮俙俛丒俙俠/乥俙俠乥乯俙俠/乥俙俠乥亅俙俛
惓幩塭偲柺愊
丂柺愊俽偺恾宍俥傪娷傓暯柺傪兛偲偟丄俥傪暯柺兝傊惓幩塭偟偨恾宍俥乫偺柺愊傪俽乫偲偡傞偲丄
丂俽乫亖俽丒們倧倱兤丂乮偨偩偟丄兤偼兛偲兝偺側偡妏乯
偙偙偱偼丄摿暿側応崌偵偮偄偰峫偊偰擺摼偟偰傕傜偆偙偲偵偟傛偆丅
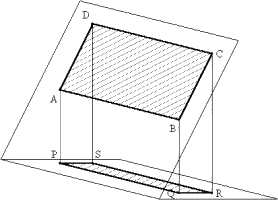 |
丂嵍恾偵偍偄偰丄挿曽宍俙俛俠俢偺柺愊俽偼丄 俽亖俙俛丒俠俢偱偁傞丅俙丄俛丄俠丄俢偺兝忋傊偺惓 幩塭傪俹丄俻丄俼丄俽偲偡傞偲偒丄俙俛偼俀暯柺兛丄 兝偺岎傢傝偲暯峴偲壖掕偟偰丄 丂丂俹俻亖俙俛丂丄丂俹俽亖俙俢丒cos兤 丂傛偭偰丄 丂丂俽乫亖俹俻丒俹俽亖俙俛丒俙俢丒們倧倱兤亖俽丒們倧倱兤 |
乮拲堄乯丂堦斒偺暯柺恾宍俥偱偼丄俥傪岎慄偵偵暯峴側曈傪帩偮挿曽宍偵嵶暘偟偰忋偲摨條
丂丂丂丂偵峫偊傟偽丄傗偼傝忋偺岞幃偼惉傝棫偮丅傕偆彮偟尩枾側徹柧偼撉幰偵擟偣傞丅
丂偙偺岞幃偵娭楢偟偨栤戣偼悢懡偄丅桳柤側栤戣傪偄偔偮偐徯夘偟傛偆丅
侾丏俷俙佦俷俛丄俷俛佦俷俠丄俷俠佦俷俙偲側偭偰偄傞巐柺懱俷俙俛俠偺係偮偺柺仮俙俛俠丄仮俷俛俠丄
丂仮俷俠俙丄仮俷俙俛偺柺愊傪偦傟偧傟俽丄俙丄俛丄俠偲偡傞偲丄俽2亖俙2亄俛2亄俠2丂偑惉傝棫偮
丂偙偲傪帵偣丅
乮摎乯丂仮俙俛俠偺朄慄儀僋僩儖傪乮倎丆倐丆們乯偲偡傞丅仮俷俛俠偺朄慄儀僋僩儖偼丄乮侾丆侽丆侽乯傛傝丄
丂們倧倱兤亖倎/併乮倎2亄倐2亄們2乯丂偱丄俙亖俽丒倎/併乮倎2亄倐2亄們2乯
摨條偵偟偰丄丂俛亖俽丒倐/併乮倎2亄倐2亄們2乯丂丄俠亖俽丒們/併乮倎2亄倐2亄們2乯
偟偨偑偭偰丄
俙2亄俛2亄俠2亖俽2乮倎2/乮倎2亄倐2亄們2乯亄倐2/乮倎2亄倐2亄們2乯亄們2/乮倎2亄倐2亄們2乯乯亖俽2
俀丏媴柺俽 丗 倶2亄倷2亄倸2亖侾 偲暯柺兛 丗 倶亄倷亄倸亖侾 偲偺岎慄傪俠偲偡傞丅俠偺 倶倷 暯柺傊
丂偺惓幩塭傪俥偲偡傞偲偒丄俥偺曽掱幃丄俥偺埻傓恾宍偺柺愊傪偦傟偧傟媮傔傛丅
乮摎乯丂倶2亄倶倷亄倷2亅倶亅倷亖侽丄倸亖侽丂丂俀兾/乮俁![]() 乯
乯
俁丏嬻娫撪偵柺愊侾偺惓嶰妏宍俙俛俠傪峫偊傞丅仮俙俛俠傪 倶倷 暯柺丄倷倸 暯柺丄倸倶 暯柺偵偦傟
丂偧傟惓幩塭偟偰弌棃傞恾宍偺柺愊傪倀丄倁丄倂偲偡傞丅嬻娫撪偱仮俙俛俠傪娷傓暯柺傪摦偐
丂偡偲偒丄倀亄倁亄倂偺嵟戝抣傪媮傔傛丅
乮摎乯丂![]()
係丏嬻娫偵壓恾偺傛偆側棫曽懱俙俛俠俢-俹俻俼俽偲偦偺懳妏慄俙俼偵悅捈側暯柺兛偑偁傞丅偙
丂偺棫曽懱偺兛傊偺惓幩塭偼惓榋妏宍偵側傞丅偙偺惓榋妏宍偺柺愊傪媮傔傛丅
乮摎乯丂俋![]()
丂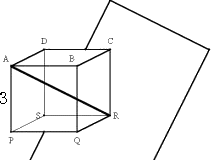
仭丂嬻娫偺昁恵庤朄偵偮偄偰
丂乽嬻娫偼偳偆傕嬯庤偩乿丄乽嬻娫偺栤戣偼恾偑昤偒偵偔偄偐傜寵偄偩乿側偳偲偄偆惡傪傛偔帹偵
偡傞偑丄乽嬻娫乿偲偼変乆偑擔忢姷傟恊偟傫偱偄傞偼偢偺乭俁師尦偺悽奅乭偵懠側傜側偄偺偩
偐傜乭姶妎偑偮偐傒偵偔偄乭偲偄偆偙偲偼側偄偼偢側偺偱偁傞丅
丂埲壓偱偼丄嬻娫摿桳偺昁恵庤朄傪惍棟偟丄墘廗偟偰偄偙偆丅
乮侾乯丂悅慄偺懌傪媮傔傞偙偲乮暯柺丒捈慄乯
乮俀乯丂揰偲暯柺乮捈慄乯偺嫍棧
乮俁乯丂暯柺乮捈慄乯偵娭偡傞懳徧揰
乮係乯丂暯柺偲暯柺丄捈慄偲捈慄丄捈慄偲暯柺偺側偡妏
乮俆乯丂捈慄傪娷傓暯柺丄暯柺偲暯柺偺岎慄
乮俇乯丂媴偲捈慄丄暯柺偲捈慄丄媴偲暯柺丄捈慄偲捈慄偺嫟桳揰
乮俈乯丂墌丄媴丄愙暯柺偺儀僋僩儖曽掱幃
楙廗侾丂丂嬻娫撪偵俀捈慄偑偁傞丅
丂丂倣 丗 倶亅侾亖乮倷亅係乯/俁亖乮倸亄侾乯/俀丂丄値 丗 倶亅倎2亖乮倷亅俀倎乯/俀亖倸亄俀丂乮倎偼幚悢乯
偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂倣偲値偼忢偵摨堦暯柺忋偵側偄偙偲傪帵偣丅
乮俀乯丂値傪娷傒丄倣偲暯峴側暯柺兾偺曽掱幃傪媮傔傛丅
乮俁乯丂尨揰偲暯柺兾偺嫍棧偑侾/![]() 偲側傞傛偆側倎偺抣傪媮傔傛丅
偲側傞傛偆側倎偺抣傪媮傔傛丅
乮摎乯乮侾乯丂棯丂乮俀乯丂倶亅倷亄倸亅倎2亄俀倎亄俀亖侽丂乮俁乯丂侾亇![]() 丄亅侾丄俁
丄亅侾丄俁
楙廗俀丂丂嬻娫偵偍偄偰丄係揰俷乮侽丆侽丆侽乯丄俙乮侾丆俀丆俁乯丄俛乮亅俀丆亅侾丆俁乯丄俠乮亅俁丆侾丆亅俀乯
丂丂丂偑偁傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂仮俙俛俠偺柺愊傪媮傔傛丅
乮俀乯丂巐柺懱俷俙俛俠偺懱愊傪媮傔傛丅
乮摎乯乮侾乯丂俁併59/俀丂乮俀乯丂俈併59/併134
楙廗俁丂丂嬻娫撪偵揰俙乮俁丆亅係丆俀![]() 乯傪拞怱偲偡傞敿宎係偺媴柺俽偲俽忋偺揰俹乮侾丆亅俀丆侽乯
乯傪拞怱偲偡傞敿宎係偺媴柺俽偲俽忋偺揰俹乮侾丆亅俀丆侽乯
丂丂丂丂偑偁傞丅俹偵偍偗傞俽偺愙暯柺傪兛偲偡傞偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂兛偺曽掱幃傪媮傔傛丅
乮俀乯丂尨揰俷偲俙偼兛偵娭偟偰摨偠懁偵偁傞偐丄斀懳懁偵偁傞偐丅
乮摎乯乮侾乯丂倶亅倷亄![]() 倸亖俁丂乮俀乯丂斀懳懁
倸亖俁丂乮俀乯丂斀懳懁
楙廗係丂丂嬻娫偺俀揰俙乮侾丆俀丆俁乯丄俛乮俆丆俇丆俈乯傪捈宎偲偡傞媴傪俽偲偡傞丅揰俻乮亅俈丆俀丆俁乯
丂丂丂偐傜俽傊偺嵟抁嫍棧倓偲偦傟傪梌偊傞俽忋偺揰偺嵗昗傪媮傔傛丅
乮摎乯丂係![]() 丂丂乮亅侾/俁丆侾侽/俁丆侾俁/俁乯
丂丂乮亅侾/俁丆侾侽/俁丆侾俁/俁乯
楙廗俆丂丂嬻娫偵係揰俙乮侾丆侽丆侽乯丄俛乮侽丆俀丆侽乯丄俠乮侽丆侽丆俀乯丄俢乮俀丆俁丆係乯偑偁傞丅師偺栤
丂丂丂偄偵摎偊傛丅
乮侾乯丂俢偐傜俁揰俙丄俛丄俠傪捠傞暯柺傊壓偟偨悅慄偺懌傪俫偲偡傞偲偒丄俫偺嵗昗傪媮傔傛丅
乮俀乯丂俫偐傜俀揰俛丄俠傪捠傞捈慄偵壓偟偨悅慄偺懌傪俲偲偡傞偲偒丄俲偺嵗昗傪媮傔傛丅
乮俁乯丂揰俹偑仮俙俛俠偺撪晹媦傃曈忋傪摦偔偲偒偺俹偲俢偺嫍棧偺嵟彫抣傪媮傔傛丅
乮摎乯乮侾乯丂乮亅侾丆俁/俀丆俆/俀乯丂乮俀乯丂乮侽丆侾/俀丆俁/俀乯丂乮俁乯丂併66/俀
楙廗俇丂丂捈慄 倣 丗 侾亅倶亖倷亄侾亖乮倸亅侾乯/係 傪娷傒丄暯柺兛 丗 係倶亅倷亅倸亖俇 偲偺側偡妏
丂丂丂丂偑係俆亱偲側傞暯柺偺曽掱幃傪媮傔傛丅
乮摎乯丂俉倶亄係倷亄倸亖俇丄俀倶亅俀倷亄倸亖俇
楙廗俈丂師偺栤偄偵摎偊傛丅
乮侾乯丂暯柺忋偺挿偝 倰 偺俀偮偺儀僋僩儖俷俙丄俷俛偼捈岎偟偰偄傞偲偡傞丅偙偺偲偒丄
丂丂俷俹亖俷俙們倧倱兤亄俷俛倱倝値兤丂乮侽亝兤亝俀兾乯丂偺揰俹偼丄偳傫側恾宍傪昤偔偐丅
乮俀乯丂嬻娫偺儀僋僩儖俷俵亖乮![]() 丆
丆![]() 丆侽乯丄俷俶亖乮侾丆亅侾丆俀乯偵懳偟偰丄
丆侽乯丄俷俶亖乮侾丆亅侾丆俀乯偵懳偟偰丄
丂俷俹亖俷俵們倧倱兤亄俷俶倱倝値兤丂乮侽亝兤亝俀兾乯丂偺揰俹偼丄偳傫側恾宍傪昤偔偐丅傑偨丄
丂俷俻亖乮俀丆侾丆侾乯偺揰俻偼偙偺恾宍忋偺揰偱偁傞偙偲傪帵偟丄偦偺偲偒偺兤偺抣傪媮傔傛丅
乮俁乯丂忋偱媮傔偨恾宍傪倶倷暯柺傊惓幩塭偟偰偱偒傞恾宍偺曽掱幃傪媮傔丄偦偺僌儔僼傪昤偗丅
乮摎乯乮侾乯丂暯柺俷俙俛忋偱俷傪拞怱偲偡傞敿宎 倰 偺墌丂乮俀乯丂慜敿偼棯丂兤亖兾/俇
丂乮俁乯丂倶2亅倶倷亄倷2亖俁
乮捛婰乯丂椷榓俇擭俉寧侾俀擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俈俉乯偺栤戣偼丄庤崰側嬻娫嵗昗偺栤戣偲尵偊傞丅
戞俁栤丂丂嬻娫偱俀偮偺暯柺 兛 丗 俀倶亄倷亄俆倸亖亅俇丄兝 丗 倸亖俀 傪峫偊傞丅兝忋偵丄
丂丂拞怱Q(俀丆侾丆俀)丄敿宎![]() 偺墌偑偁傝丄偦偺廃忋偵揰C偑偁傞丅偨偩偟丄C偼兛偵娭偟
偺墌偑偁傝丄偦偺廃忋偵揰C偑偁傞丅偨偩偟丄C偼兛偵娭偟
丂丂偰Q偲摨偠懁偵偁傞傕偺偲偡傞丅偙偺偲偒丄師偺栤偵摎偊傛丅
乮侾乯丂俠偐傜兛偵壓傠偟偨悅慄偺懌傪T偲偡傞丅CT偺挿偝偑![]() 偱偁傞偲偒丄CT傪媮傔傛丅
偱偁傞偲偒丄CT傪媮傔傛丅
乮俀乯丂俠偍傛傃俿偺嵗昗傪媮傔傛丅
乮夝乯乮侾乯丂(俀丆侾丆俆)佦兛丂傛傝丄丂俠俿亖倠(俀丆侾丆俆)丂乮倠偼幚悢乯丂偲偍偗傞丅
丂俠俿亖![]() 丂傛傝丄倠2乮係亄侾亄俀俆乯亖俁侽丂偐傜丄倠2亖侾丂偡側傢偪丄倠亖亇侾
丂傛傝丄倠2乮係亄侾亄俀俆乯亖俁侽丂偐傜丄倠2亖侾丂偡側傢偪丄倠亖亇侾
俥乮倶丆倷丆倸乯亖俀倶亄倷亄俆倸亄俇丂偲偍偔偲丄丂俥乮俀丆侾丆俀乯亖係亄侾亄侾侽亄俇亖俀侾亜侽丂側偺偱丄
俠乮倫丆倯丆俀乯偵懳偟偰丄丂俥乮倫丆倯丆俀乯亖俀倫亄倯亄侾俇亜侽丂偱偁傞丅
偙偺偲偒丄丂俿乮倫亄俀倠丆倯亄倠丆俀亄俆倠乯丂偑兛忋偵偁傞偺偱丄
丂俀乮倫亄俀倠乯亄乮倯亄倠乯亄俆乮俀亄俆倠乯亖亅俇丂偡側傢偪丄丂俀倫亄倯亄侾俇亄俁侽倠亖侽
俀倫亄倯亄侾俇亜侽丂傛傝丄倠亙侽丂偱偁傞偙偲偑暘偐傞丅丂傛偭偰丄倠亖亅侾丂偱偁傞丅
丂傛偭偰丄俠俿亖(亅俀丆亅侾丆亅俆)
乮俀乯丂乮侾乯傛傝丄丂俀倫亄倯亖侾係丂偱偁傞丅
偙偙偱丄丂俠俻亖![]() 丂傛傝丄丂乮倫亅俀乯2亄乮倯亅侾乯2亖俀俋
丂傛傝丄丂乮倫亅俀乯2亄乮倯亅侾乯2亖俀俋
倯亖侾係亅俀倫丂傪戙擖偟偰惍棟偡傞偲丄丂俆倫2亅俆俇倫亄侾係係亖侽
偡側傢偪丄丂乮俆倫亅俁俇乯乮倫亅係乯亖侽丂傛傝丄丂倫亖俁俇/俆丂丄係
倫亖俁俇/俆丂偺偲偒丄丂倯亖侾係亅俀倫亖亅俀/俆
倫亖係丂偺偲偒丄丂倯亖俇
埲忋偐傜丄丂俠乮俁俇/俆丆亅俀/俆丆俀乯丂傑偨偼丄丂俠乮係丆俇丆俀乯
俠乮俁俇/俆丆亅俀/俆丆俀乯丂偺偲偒丄丂俿乮俀俇/俆丆亅俈/俆丆亅俁乯
俠乮係丆俇丆俀乯丂偺偲偒丄丂俿乮俀丆俆丆亅俁乯丂丂乮廔乯
乮捛婰乯丂椷榓俇擭俉寧俀係擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俈俋乯偺栤戣傕丄嬻娫偵偍偗傞昁恵媄朄偲尵偊傞偩傠偆丅
戞侾栤丂丂乮侾乯丂俁揰俙(俀丆侽丆俀)丄俛(俀丆俀丆侾)丄俠(侽丆侽丆俁)傪捠傞暯柺偺曽掱幃傪媮傔傛丅
丂丂乮俀乯丂尨揰俷偐傜偙偺暯柺偵壓傠偟偨悅慄偺懌傪俢偲偡傞丅俢偺嵗昗傪媮傔丄俷俙偲俷俢
丂丂丂偺側偡妏傪媮傔傛丅
乮夝乯乮侾乯丂媮傔傞暯柺偺曽掱幃傪丄丂倎倶亄倐倷亄們倸亖倓丂偲偍偔偲丄俁揰俙丄俛丄俠傪捠傞偙偲偐傜丄
丂俀倎亄俀們亖倓丂丄俀倎亄俀倐亄們亖倓丂丄俁們亖倓丂偑惉傝棫偮丅
偡側傢偪丄丂俀倎亖們丂丄俀倐亖們丂側偺偱丄丂乮侾/俀乯們倶亄乮侾/俀乯們倷亄們倸亖俁們
們亗侽丂偲偟偰丄媮傔傞暯柺偺曽掱幃偼丄丂倶亄倷亄俀倸亖俇
乮俀乯丂乮侾丆侾丆俀乯佦倶亄倷亄俀倸亖俇丂側偺偱丄俢乮倲丆倲丆俀倲乯丂偲偍偗傞丅
丂偙偺揰偑暯柺忋偵偁傞偺偱丄丂倲亄倲亄係倲亖俇丂偐傜丄倲亖侾丂傛偭偰丄俢乮侾丆侾丆俀乯
丂俷俙亖(俀丆侽丆俀)丄俷俢亖(侾丆侾丆俀)丂偐傜丄丂俷俙亖俀![]() 丄俷俢亖
丄俷俢亖![]() 丂偱丄俷俙丒俷俢亖俇
丂偱丄俷俙丒俷俢亖俇
傛偭偰丄俷俙偲俷俢偺側偡妏傪兤偲偍偔偲丄丂們倧倱兤亖俇/乮俀![]() 丒
丒![]() 乯亖
乯亖![]() /俀丂偐傜丄
/俀丂偐傜丄
兤亖俁侽亱丂丂乮廔乯
乮捛婰乯丂椷榓俇擭俋寧侾俇擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉侽乯偺栤戣傕丄嬻娫偵偍偗傞昁恵媄朄偲尵偊傞偩傠偆丅
栤戣丂丂尨揰俷偐傜捈慄 乮倶亅俀乯/俁亖乮倷亅侾乯/係亖乮侾亅倸乯/俆 偵壓傠偟偨悅慄偺挿偝傪媮傔傛丅
乮夝乯丂乮倶亅俀乯/俁亖乮倷亅侾乯/係亖乮侾亅倸乯/俆亖倲丂偲偍偔偲丄倶亖俁倲亄俀丄倷亖係倲亄侾丄倸亖侾亅俆倲
傛偭偰丄丂倶2亄倷2亄倸2亖俆侽倲2亄侾侽倲亄俇亖俆侽乮倲亄侾/侾侽乯2亄侾侾/俀丂傛傝丄
倲亖亅侾/侾侽丂偺偲偒嵟彫偱丄嵟彫抣偼丄併乮侾侾/俀乯亖乮侾/俀乯併俀俀丂丂乮廔乯
乮暿夝乯丂乮俁倲亄俀丆係倲亄侾丆侾亅俆倲乯佦乮俁丆係丆亅俆乯丂傛傝丄
丂俁乮俁倲亄俀乯亄係乮係倲亄侾乯亅俆乮侾亅俆倲乯亖俆侽倲亄俆亖侽丂傛偭偰丄丂倲亖亅侾/侾侽
偙偺偲偒丄悅慄偺懌偺嵗昗偼丄乮侾俈/侾侽丆俁/俆丆俁/俀乯丂偱丄悅慄偺挿偝偼丄
丂併乮俀俉俋/侾侽侽亄俋/俀俆亄俋/係乯亖併乮侾侾/俀乯亖乮侾/俀乯併俀俀丂丂乮廔乯
乮捛婰乯丂椷榓俇擭俋寧俀俈擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉侾乯偺栤戣傕丄嬻娫偵偍偗傞昁恵媄朄偲尵偊傞偩傠偆丅
栤戣侾丂丂師偺俀暯柺偑梌偊傜傟偰偄傞丅丂兛丗係倶亄侾俀倷亅俁倸亖侾俀丂丄兝丗俉倶亅俋倷亄俆倸亖亅俋
丂丂偙偺偲偒丄暯柺兛偲兝偺岎傢傝偺捈慄曽岦偺扨埵儀僋僩儖 倳 傪媮傔傛丅傑偨丄暯柺兛偵
丂丂暯峴偱 倳 偵悅捈側扨埵儀僋僩儖 倴 傪媮傔傛丅偨偩偟丄倳丄倴 偺 倶 惉暘偼偄偢傟傕惓偲偡傞丅
乮夝乯丂暯柺兛偲兝偺岎傢傝偺捈慄曽岦偺儀僋僩儖傪 倓亖乮倎丆倐丆們乯 偲偍偔偲丄戣堄傛傝丄
丂乮倎丆倐丆們乯佦乮係丆侾俀丆亅俁乯丂丄乮倎丆倐丆們乯佦乮俉丆亅俋丆俆乯丂側偺偱丄
丂係倎亄侾俀倐亅俁們亖侽丂丄丂俉倎亅俋倐亄俆們亖侽丂傛傝丄們亖俁倐丂丄倎亖亅乮俁/係乯倐
傛偭偰丄丂倓亖乮亅俁/係丆侾丆俁乯倐丂偱丄乮亅俁/係丆侾丆俁乯偺戝偒偝偼丄侾俁/係
埲忋偐傜丄媮傔傞扨埵儀僋僩儖 倳 偼丄丂乮俁/侾俁丆亅係/侾俁丆亅侾俀/侾俁乯
丂暯柺兛偵暯峴偱 倳 偵悅捈側儀僋僩儖傪丄倴乫亖乮倱丆倲丆倳乯 偲偍偔偲丄
戣堄傛傝丄丂係倱亄侾俀倲亅俁倳亖侽丂丄俁倱亅係倲亅侾俀倳亖侽丂側偺偱丄
丂倱亖俁倳丂丄倲亖亅乮俁/係乯倳丂傛傝丄丂倴乫亖乮俁丆亅俁/係丆侾乯倳
丂乮俁丆亅俁/係丆侾乯偺戝偒偝偼丄侾俁/係丂側偺偱丄媮傔傞扨埵儀僋僩儖倴 偼丄
丂倴亖乮侾俀/侾俁丆亅俁/侾俁丆係/侾俁乯丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侽寧俀俆擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉俁乯偺栤戣傕丄嬻娫偵偍偗傞昁恵媄朄偲尵偊傞偩傠偆丅
栤戣丂丂嬻娫撪偺係揰俷(侽丆侽丆侽)丄俙(侽丆侾丆亅侾)丄俹(亅俀倲丆侽丆侽)丄俻(倲丆倲亄侾丆倲亅侾) (倲亗侽)
丂丂傪峫偊傞丅俁揰俷丄俹丄俻傪捠傞暯柺偑俁揰俙丄俹丄俻傪捠傞暯柺偵悅捈偵側傞傛偆偵 倲 傪掕
丂丂傔傛丅
乮夝乯丂仮俷俹俻偺朄慄儀僋僩儖傪乮倎丆倐丆們乯丄仮俙俹俻偺朄慄儀僋僩儖傪乮倠丆倣丆値乯丂偲偡傞偲丄
亅俀倲倎亖侽丄倎倲亄倐乮倲亄侾乯亄們乮倲亅侾乯亖侽丂偐傜丄倎亖侽丂偱丄乮倎丆倐丆們乯亖乮侽丆倲亅侾丆亅倲亅侾乯
傑偨丄亅俀倲倠亅倣亄値亖侽丂丄倠亄倣亄値亖侽丂偐傜丄乮倠丆倣丆値乯亖乮俀丆亅俀倲亅侾丆俀倲亅侾乯
乮倎丆倐丆們乯佦乮倠丆倣丆値乯丂偐傜丄丂亅乮俀倲亄侾乯乮倲亅侾乯亅乮俀倲亅侾乯乮倲亄侾乯亖侽
傛偭偰丄丂俀倲2亖侾丂偐傜丄丂倲亖亇侾/![]() 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侾寧係擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉係乯偺栤戣傕丄嬻娫偵偍偗傞昁恵媄朄偲尵偊傞偩傠偆丅
栤戣丂丂嬻娫偵俁揰俙(亅俀丆俀丆亅侾/俀乯丄俛乮侾丆侽丆侾/俀乯丄俹(俀倫丆倫丆俁倫乯偑偁傞丅
乮侾乯丂俷傪尨揰偲偡傞偲偒丄俀偮偺儀僋僩儖AB丄OP偺側偡妏傪媮傔傛丅偨偩偟丄倫亗侽 偲偡傞丅
乮俀乯丂揰俹傛傝捈慄AB偵壓傠偟偨悅慄偺挿偝偑![]() /俀偵側傞傛偆偵倫偺抣傪媮傔傛丅
/俀偵側傞傛偆偵倫偺抣傪媮傔傛丅
乮夝乯乮侾乯丂AB亖乮俁丆亅俀丆侾乯丄OP亖乮俀倫丆倫丆俁倫乯丂傛傝丄AB丄OP偺側偡妏兤偼丄
丂們倧倱兤亖倫/乮俀乥倫乥乯亖亇侾/俀丂傛傝丄丂兤亖兾/俁丂傑偨偼丂俀兾/俁
乮俀乯丂揰俹傛傝捈慄AB偵壓傠偟偨悅慄偺懌傪俫偲偍偔偲丄丂俙俫亖倠俙俛亖乮俁倠丆亅俀倠丆倠乯
偙偺偲偒丄丂俹俫亖乮俁倠亅俀倫亅俀丆亅俀倠亅倫亄俀丆倠亅俁倫亅侾/俀乯
俹俫亖![]() /俀丂傛傝丄丂乮俁倠亅俀倫亅俀乯2亄乮亅俀倠亅倫亄俀乯2亄乮倠亅俁倫亅侾/俀乯2亖俆/係
/俀丂傛傝丄丂乮俁倠亅俀倫亅俀乯2亄乮亅俀倠亅倫亄俀乯2亄乮倠亅俁倫亅侾/俀乯2亖俆/係
俙俛佦俹俫丂傛傝丄丂俁乮俁倠亅俀倫亅俀乯亅俀乮亅俀倠亅倫亄俀乯亄倠亅俁倫亅侾/俀亖侽
偡側傢偪丄丂倫亖俀倠亅俁/俀
傛偭偰丄丂乮亅倠亄侾乯2亄乮亅係倠亄俈/俀乯2亄乮亅俆倠亄係乯2亖俆/係丂傛傝丄
丂係俀倠2亅俈侽倠亄俀俉亖侽丂偐傜丄丂俁倠2亅俆倠亄俀亖侽
偡側傢偪丄丂乮俁倠亅俀乯乮倠亅侾乯亖侽丂傛傝丄丂倠亖俀/俁丂丄侾
偙偺偲偒丄丂倫亖亅侾/俇丂丄侾/俀丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侾寧係擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俆乯偺栤戣偼丄嬻娫攃埇偑弌棃偰偄傟偽堈栤偩傠偆丅
栤戣俇丂丂暯柺 倶亄俀倷亄俀倸亖俋 忋偵揰俙(俆丆亅侾丆俁)傪拞怱偲偡傞敿宎俀偺墌傪昤偔丅揰俹偑
丂丂偙偺墌廃忋傪摦偔偲偒丄O俹偺暯曽偺嵟彫抣傪媮傔傛丅偨偩偟丄俷偼尨揰偲偡傞丅
乮夝乯丂俷傛傝暯柺偵壓偟偨悅慄偺懌俫偺嵗昗偼丄乮倲丆俀倲丆俀倲乯丂偲偍偗傞丅偙偺揰偑暯柺忋偵
偁傞偺偱丄丂倲亄係倲亄係倲亖俋丂傛傝丄丂倲亖侾丂傛偭偰丄俫乮侾丆俀丆俀乯
偙偺偲偒丄丂俙俫2亖侾俇亄俋亄侾亖俀俇亜係丂偐傜丄俫偼墌奜偺揰偱偁傞丅
傛偭偰丄丂俷俹2亖俷俫2亄俹俫2亖俹俫2亄俋丂偵偍偄偰丄俹俫亖![]() 亅俀丂偺偲偒嵟彫偲側傞丅
亅俀丂偺偲偒嵟彫偲側傞丅
偟偨偑偭偰丄俷俹2偺嵟彫抣偼丄丂乮![]() 亅俀乯2亄俋亖俁俋亅係
亅俀乯2亄俋亖俁俋亅係![]() 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侾寧侾俈擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉俆乯偺栤戣傕揟宆揑側嬻娫恾宍偺栤戣偱偁傞丅
栤戣丂丂嬻娫撪偺俁捈慄 俴0丗倷亖倸亖侽丂丄俴1丗倶/俀亖倷亖倸亅侾丂丄俴2丗亅倶亖倷亖倸亄侾丂傪峫偊
丂丂傞丅俴0忋偺揰俹(倲丆侽丆侽) 偵懳偟丄俹傪捠傝丄俴1丄俴2 偲岎傢傞捈慄傪俧偲偡傞丅
乮侾乯丂俧偺曽掱幃傪媮傔傛丅
乮俀乯丂俧偲俴1丄俴2 偲偺岎揰傪偦傟偧傟俻丄俼偲偡傞丅俹偑俴0忋傪摦偔偲偒丄俻俼偺嵟彫抣傪媮傔
丂傛丅
乮夝乯乮侾乯丂俧偲俴1丄俴2 偲偺岎揰俻丄俼偵偮偄偰丄俻乮俀倣丆倣丆倣亄侾乯丄俼乮亅値丆値丆値亅侾乯偲偡傞丅
偙偺偲偒丄俻俼亖乮俀倣亄値丆倣亅値丆倣亅値亄俀乯亖倠俹俼亖倠乮亅値亅倲丆値丆値亅侾乯丂偱偁傞丅
丂俀倣亄値亖亅倠値亅倠倲丂丄倣亅値亖倠値丂丄倣亅値亄俀亖倠値亅倠
戞俀丄俁幃傛傝丄丂倠亖亅俀丂側偺偱丄丂俀倣亅値亖俀倲丂丄丂倣亄値亖侽
傛偭偰丄丂値亖亅倣丂傛傝丄丂倣亖乮俀/俁乯倲丂丄値亖亅乮俀/俁乯倲丂側偺偱丄
俻俼亖乮俀倣亄値丆倣亅値丆倣亅値亄俀乯亖乮乮俀/俁乯倲丆乮係/俁乯倲丆乮係/俁乯倲亄俀乯
亖乮俀/俁乯乮倲丆俀倲丆俀倲亄俁乯
偟偨偑偭偰丄捈慄俧偺曽掱幃偼丄丂乮倶亅倲乯/倲亖倷/乮俀倲乯亖倸/乮俀倲亄俁乯丂偲側傞丅
乮俀乯丂俻俼亖乮俀/俁乯乮倲丆俀倲丆俀倲亄俁乯丂傛傝丄
俻俼2亖乮係/俋乯乮倲2亄係倲2亄乮俀倲亄俁乯2乯
亖乮係/俋乯乮俋倲2亄侾俀倲亄俋乯亖乮係/俋乯乮俋乮倲亄俀/俁乯2亄俆乯丂偐傜丄倲亖亅俀/俁丂偺偲偒丄嵟彫
傛偭偰丄俻俼偺嵟彫抣偼丄丂乮俀/俁乯![]() 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侾寧侾俉擔晅偗
丂師偺搶杒戝妛丂暥棟嫟捠乮侾俋俉俇乯偺栤戣偼丄婎杮儀僋僩儖偑榖戣偵側偭偰偍傝丄怴慛側姶
偠偑偡傞丅
栤戣丂丂嬻娫偵偍偗傞婎杮儀僋僩儖 倕亖乮侾丆侽丆侽乯丄倖亖乮侽丆侾丆侽乯丄倞亖乮侽丆侽丆侾乯 傪巊偭偰丄
丂丂俁偮偺儀僋僩儖 倎丄倐丄們 傪丄倎亖倕亄倖丄倐亖倕亅倖丄們亖亅倕亄倞 偲掕傔傞丅
乮侾乯丂倎 偲 倐丄倐 偲 們丄們 偲 倎 偺側偡妏傪偦傟偧傟媮傔傛丅
乮俀乯丂俀偮偺儀僋僩儖 倐丄們 偵捈岎偟丄儀僋僩儖 倎 偲偺撪愊偑侾偱偁傞傛偆側傋僋僩儖傪 倫 偲
丂丂偡傞丅倫 傪婎杮儀僋僩儖 倕丄倖丄倞 偱昞偣丅
乮夝乯乮侾乯丂倎亖乮侾丆侾丆侽乯丄倐亖乮侾丆亅侾丆侽乯丄們亖乮亅侾丆侽丆侾乯丂傛傝丄
丂們倧倱乮倎丆倐乯亖侽丂偐傜丄乮倎丆倐乯亖兾/俀
丂們倧倱乮倐丆們乯亖亅侾/俀丂偐傜丄乮倐丆們乯亖俀兾/俁
丂們倧倱乮們丆倎乯亖亅侾/俀丂偐傜丄乮們丆倎乯亖俀兾/俁
乮俀乯丂倫亖乮倶丆倷丆倸乯丂偲偍偔偲丄倫丒倐亖倶亅倷亖侽丂丄倫丒們亖亅倶亄倸亖侽丂傛傝丄倶亖倷亖倸
丂傑偨丄倫丒倎亖倶亄倷亖侾丂偐傜丄丂倶亖倷亖倸亖侾/俀
丂傛偭偰丄丂倫亖乮侾/俀丆侾/俀丆侾/俀乯亖乮侾/俀乯倕亄乮侾/俀乯倖亄乮侾/俀乯倞丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾俀寧俁擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俈乯偺栤戣偼丄揰偲暯柺偲偺嫍棧偺岞幃偑妶桇偡傞丅
栤戣俆丂丂倶倷 暯柺偲偺岎傢傝偑墌 乮倶亄侾乯2亄倷2亖俀 偲側傝丄暯柺 係倶亄俀![]() 倷亅倸亖係 偵愙
倷亅倸亖係 偵愙
丂丂偡傞媴偺曽掱幃傪媮傔傛丅
乮夝乯丂戣堄傛傝丄媴偺拞怱偺嵗昗偼丄乮亅侾丆侽丆倎乯丂乮倎偼幚悢乯丂偲偍偗傞丅
偙偺揰乮亅侾丆侽丆倎乯偲暯柺 係倶亄俀![]() 倷亅倸亖係 偺嫍棧偼丄丂乥倎亄俉乥/俆丂偱丄
倷亅倸亖係 偺嫍棧偼丄丂乥倎亄俉乥/俆丂偱丄
媴偺敿宎丂併乮倎2亄俀乯丂偵摍偟偄丅偡側傢偪丄丂乥倎亄俉乥/俆亖併乮倎2亄俀乯
椉曈傪暯曽偟偰惍棟偡傞偲丄丂侾俀倎2亅俉倎亅俈亖侽丂偡側傢偪丄丂乮俀倎亄侾乯乮俇倎亅俈乯亖侽
傛偭偰丄丂倎亖亅侾/俀丂丄俈/俇
倎亖亅侾/俀丂偺偲偒丄媴偺敿宎偼丄併乮俋/係乯亖俁/俀
倎亖俈/俇丂偺偲偒丄媴偺敿宎偼丄併乮侾俀侾/俁俇乯亖侾侾/俇
偟偨偑偭偰丄媮傔傞媴偺曽掱幃偼丄
丂乮倶亄侾乯2亄倷2亄乮倸亄侾/俀乯2亖俋/係丂丄乮倶亄侾乯2亄倷2亄乮倸亅俈/俇乯2亖侾俀侾/俁俇丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾寧俇擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉俉乯偺栤戣偼丄嶰妏宍丄巐柺懱偺廳怱偵娭傢傞栤戣偱偁傞丅
栤戣丂丂巐柺懱OABC偵偍偄偰丄OA亖倎丄OB亖倐丄OC亖們 偲偟丄G傪仮ABC偺廳怱丄懄偪丄
丂丂俷俧亖乮倎亄倐亄們乯/俁 偲偡傞丅
乮侾乯丂俷俧亖倗 偲偍偄偰丄俙俧2傪 倎丄倗 偍傛傃撪愊傪梡偄偰昞偣丅
乮俀乯丂俷俙2亄俷俛2亄俷俠2亖AG2亄BG2亄CG2亄俁OG2 傪帵偣丅
乮俁乯丂仮OAB偺廳怱傪俤偲偡傞丅俷俥亖乮俁/係乯俷俧偵傛偭偰丄揰俥傪掕傔傞偲偒丄俥偼捈慄CE忋
丂丂偵偁傞偙偲傪帵偣丅
乮夝乯乮侾乯丂俙俧亖倗亅倎丂傛傝丄丂俙俧2亖乮倗亅倎乯丒乮倗亅倎乯亖乥倗乥2亅俀倗丒倎亄乥倎乥2
乮俀乯丂乮侾乯偲摨條偵偟偰丄丂BG2亖乥倗乥2亅俀倗丒倐亄乥倐乥2丄CG2亖乥倗乥2亅俀倗丒們亄乥們乥2
傛偭偰丄AG2亄BG2亄CG2亄俁OG2
亖乥倎乥2亄乥倐乥2亄乥們乥2亅俀倗丒乮倎亄倐亄們乯亄俁乥倗乥2亄俁乥倗乥2
亖乥倎乥2亄乥倐乥2亄乥們乥2亅俇乥倗乥2亄俇乥倗乥2
亖乥倎乥2亄乥倐乥2亄乥們乥2
亖俷俙2亄俷俛2亄俷俠2
傛偭偰丄丂俷俙2亄俷俛2亄俷俠2亖AG2亄BG2亄CG2亄俁OG2 偑惉傝棫偮丅
乮俁乯丂俷俤亖乮倎亄倐乯/俁丂丄俷俥亖乮俁/係乯俷俧亖乮倎亄倐亄們乯/係丂側偺偱丄
俠俥亖乮倎亄倐亄們乯/係亅們亖乮倎亄倐亅俁們乯/係丂丄俠俤亖乮倎亄倐乯/俁亅們亖乮倎亄倐亅俁們乯/俁
傛偭偰丄丂俠俥亖乮俁/係乯俠俤丂傛傝丄俥偼捈慄CE忋偵偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾寧侾侽擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俋乯偺栤戣偼丄嬻娫攃埇傪偟偰峫偊傞偲妝偟偄丅
栤戣侾丂丂倶倷倸嬻栤偵偍偄偰丄揰(侽丆侽丆俆)傪俹丄暯柺 倶亄俀倷亄俀倸亖侽 傪兛偲偟丄倶倷暯柺忋偺
丂丂墌 倶2亄倷2亖係 傪俠偲偡傞丅
乮侾乯丂暯柺兛偲倶倷暯柺偲偺岎慄偺曽岦儀僋僩儖 倎亖乮俀丆倎2丆倎3乯 偲丄倎偵悅捈偱暯柺兛偵暯
丂峴側儀僋僩儖倐亖乮俀丆倐2丆倐3乯 傪媮傔傛丅
乮俀乯丂尨揰俷偲兛忋偺揰Q偵懳偟 OQ亖倱倎亄t倐 偲偍偔丅捈慄PQ偑墌俠偲岎傢傞偨傔偺 倱丄倲
丂偺枮偨偡傋偒忦審傪媮傔傛丅
乮夝乯乮侾乯丂乮侾丆俀丆俀乯佦乮俀丆倎2丆倎3乯 偐傜丄丂倎2亄倎3亖亅侾
丂倎偼丄暯柺兛偲 倶倷 暯柺偲偺岎慄偺曽岦儀僋僩儖側偺偱丄丂倎3亖侽丂傛偭偰丄丂倎2亖亅侾
丂傛偭偰丄丂倎亖乮俀丆亅侾丆侽乯
傑偨丄倐偼丄倎偵悅捈側偺偱丄丂係亅倐2亖侽丂偐傜丄丂倐2亖係
偝傜偵丄倐佦乮侾丆俀丆俀乯丂傛傝丄丂俀亄俉亄俀倐3亖侽丂偐傜丄丂倐3亖亅俆
丂傛偭偰丄丂倐亖乮俀丆係丆亅俆乯
乮俀乯丂OQ亖倱倎亄t倐亖乮俀倱亄俀倲丆亅倱亄係倲丆亅俆倲乯 側偺偱丄
丂俹俻亖乮俀倱亄俀倲丆亅倱亄係倲丆亅俆倲亅俆乯
傛偭偰丄捈慄俹俻偺曽掱幃偼丄丂倶/乮俀倱亄俀倲乯亖倷/乮亅倱亄係倲乯亖乮倸亅俆乯/乮亅俆倲亅俆乯
偙偺偲偒丄倶倷暯柺偲偺岎揰偼丄倸亖侽 偲偟偰丄倶亖乮俀倱亄俀倲乯/乮倲亄侾乯丄倷亖乮亅倱亄係倲乯/乮倲亄侾乯
偙偺揰偑俠忋偵偁傞偨傔偺忦審偼丄丂乮俀倱亄俀倲乯2/乮倲亄侾乯2亄乮亅倱亄係倲乯2/乮倲亄侾乯2亖係
偡側傢偪丄丂乮俀倱亄俀倲乯2亄乮亅倱亄係倲乯2亖係乮倲亄侾乯2丂傛傝丄
丂俆倱2亄侾俇倲2亅俉倲亅係亖侽丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾寧侾俋擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉俋乯偺栤戣偼丄奊偑昤偗傟偽夝偒傗偡偄偐側丠
栤戣丂丂乮侾乯丂媴 倶2亄倷2亄倸2亄俀倶亅係倷亄係倸亖侾俇 偺暯柺 俇倶亅俀倷亄俁倸亖俆 偵傛傞愗傝岥
丂丂偱偁傞墌俠偺拞怱偲敿宎傪媮傔傛丅
乮俀乯丂墌俠忋偺偡傋偰偺揰偐傜偺嫍棧偑併俁俀偱偁傞揰傪媮傔傛丅
乮夝乯乮侾乯丂倶2亄倷2亄倸2亄俀倶亅係倷亄係倸亖侾俇 傛傝丄丂乮倶亄侾乯2亄乮倷亅俀乯2亄乮倸亄俀乯2亖俀俆
傛偭偰丄媴偺拞怱偼丄乮亅侾丆俀丆亅俀乯丂偱丄敿宎偼丄俆
丂揰乮亅侾丆俀丆亅俀乯偲暯柺 俇倶亅俀倷亄俁倸亖俆 偺嫍棧偼丄
丂乥亅俇亅係亅俇亅俆乥/併乮俁俇亄係亄俋乯亖俀侾/俈亖俁
傛偭偰丄墌俠偺敿宎偼丄丂併乮俀俆亅俋乯亖係
傑偨丄捈慄丂乮倶亄侾乯/俇亖乮倷亅俀乯/乮亅俀乯亖乮倸亄俀乯/俁丂偲暯柺 俇倶亅俀倷亄俁倸亖俆 偺岎揰偼丄
丂俇乮俇倲亅侾乯亅俀乮亅俀倲亄俀乯亄俁乮俁倲亅俀乯亖俆丂偐傜丄丂倲亖俁/俈丂側偺偱丄
墌俠偺拞怱偼丄乮侾侾/俈丆俉/俈丆亅俆/俈乯乯
乮俀乯丂媮傔傞揰偺嵗昗偼丄乮俇倲亅侾丆亅俀倲亄俀丆俁倲亅俀乯丂偲偍偗傞丅
偙偺偲偒丄丂乮俇倲亅侾俉/俈乯2亄乮亅俀倲亄俇/俈乯2亄乮俁倲亅俋/俈乯2亖俁俀亅侾俇亖侾俇
揥奐偟偰惍棟偡傞偲丄丂俈倲2亅俇倲亅侾亖侽丂偐傜丄丂倲亖侾丄亅侾/俈
倲亖侾丂偺偲偒丄媮傔傞揰偼丄丂乮俆丆侽丆侾乯
倲亖亅侾/俈丂偺偲偒丄媮傔傞揰偼丄丂乮亅侾俁/俈丆侾俇/俈丆亅侾俈/俈乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俁寧係擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋侽乯偺栤戣偼丄傛偔楙傜傟偨栤戣偱偁傞丅
栤戣丂丂倶倷倸 嬻娫偵偍偗傞媴柺 俛丗乮倶亅俁乯2亄乮倷亅係乯2亄乮倸亅侾俀乯2亖侾俁2 偵偮偄偰峫偊傞丅
乮侾乯丂媴柺俛忋偺揰俷乮侽丆侽丆侽乯傪捠傝丄媴柺俛偵愙偡傞暯柺俫偺曽掱幃傪媮傔傛丅
乮俀乯丂暯柺俫忋偺揰俹傪丄俹傪拞怱偲偡傞敿宎侾偺媴柺偑俛偲岎傢傞傛偆偵摦偐偡丅
丂丂揰俿乮俋丆侾俀丆俁俇乯偲揰俹偲傪寢傫偱偱偒傞慄暘慡懱偑嶌傞棫懱乮俿傪捀揰偲偡傞悕懱乯傪俤
丂丂偲偡傞丅俤偺懱愊倁傪媮傔傛丅
丂丂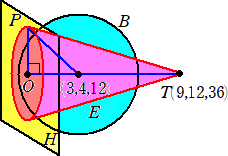
乮夝乯乮侾乯丂俫 丗 俁倶亄係倷亄侾俀倸亖侽
乮俀乯丂俷俹2亖侾係2亅侾俁2亖俀俈丂側偺偱丄俤偺掙柺偼丄敿宎俁![]() 偺墌
偺墌
丂俿乮俋丆侾俀丆俁俇乯偲暯柺俫偺嫍棧偼丄
丂乮俁丒俋亄係丒侾俀亄侾俀丒俁俇乯/併乮俁2亄係2亄侾俀2乯亖俆侽俈/侾俁亖俁俋
傛偭偰丄媮傔傞懱愊倁偼丄丂倁亖俀俈兾丒俁俋丒乮侾/俁乯亖俁俆侾兾丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俁寧俀侽擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋侽乯偺栤戣偼丄媮愊偺婎杮宍偩傠偆丅
栤戣丂丂xyz嬻娫偺拞偺俀揰俙(侾丆侽丆侾)丄俛(-1丆侽丆侾)傪寢傇捈慄傪L偲偟丄xy暯柺偵偍偗傞墌
丂丂x2亄y2亖侾傪俢偲偡傞丅揰俹偑俴忋傪摦偒丄揰俻偑D忋傪摦偔偲偒丄慄暘PQ偑摦偄偰偱偒傞
丂丂棫懱傪俫偲偡傞丅暯柺z亖t (侽亝倲亝侾)偵傛傞棫懱H偺愗傝岥Ht偺柺愊俽t偲俫偺懱愊V傪媮
丂丂傔傛丅
乮夝乯丂戣堄傛傝丄捈慄俴忋偺揰俹乮倫丆侽丆侾乯丂乮亅侾亝倫亝侾乯丂偲偍偗傞丅
丂傑偨丄俢忋偺揰俻乮倰們倧倱兤丆倰倱倝値兤丆侽乯丂乮侽亝倰亝侾丄侽亝兤亝俀兾乯丂偲偍偗傞丅
偙偺偲偒丄捈慄俹俻偺曽掱幃偼丄丂乮倶亅倫乯/乮倰們倧倱兤亅倫乯亖倷/乮倰倱倝値兤乯亖乮倸亅侾乯/乮亅侾乯
偙偺捈慄偲暯柺 倸亖倲 偲偺岎揰偼丄
丂倶亖倫亄乮侾亅倲乯丒乮倰們倧倱兤亅倫乯亖倫倲亄乮侾亅倲乯丒倰們倧倱兤丂丄倷亖乮侾亅倲乯丒乮倰倱倝値兤乯
傛傝丄丂乮倶亅倫倲乯2亄倷2亖乮侾亅倲乯2丒倰2
偡側傢偪丄丂乮倶亅倫倲乯2亄倷2亝乮侾亅倲乯2丂偨偩偟丄亅侾亝倫亝侾丄侽亝倲亝侾
偙傟偼丄倶倷暯柺偱丄乮倫倲丆侽乯傪拞怱偲偟丄敿宎 侾亅倲 偺墌偺撪晹偍傛傃廃偱偁傞丅
丂摿偵丄丂倫亖亅侾 偺偲偒丄丂乮倶亄倲乯2亄倷2亝乮侾亅倲乯2
丂倫亖侽 偺偲偒丄丂倶2亄倷2亝乮侾亅倲乯2
丂倫亖侾 偺偲偒丄丂乮倶亅倲乯2亄倷2亝乮侾亅倲乯2
偟偨偑偭偰丄丂俽t亖兾乮侾亅倲乯2亄俀倲丒俀乮侾亅倲乯亖兾乮侾亅倲乯2亄係倲乮侾亅倲乯
傑偨丄倁亖佺01 乮兾乮侾亅倲乯2亄係倲乮侾亅倲乯乯倓倲亖[亅兾乮侾亅倲乯3/俁亄俀倲2亅乮係/俁乯倲3]01
丂亖俀亅係/俁亄兾/俁亖乮兾亄俀乯/俁丂丂乮廔乯
乮捛婰乯丂椷榓俈擭係寧係擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋侾乯偺栤戣偼丄慺杙側愙暯柺偺寁嶼偱偁傞丅
栤戣丂丂乮侾乯丂媴柺 倶2亄倷2亄倸2亅俀倸亖侽 偵愙偟丄捈慄 倶亄倷亅倠亖倸亖侽 乮倠亜侽乯 傪娷傓俀
丂丂偮偺暯柺偺曽掱幃傪媮傔傛丅傑偨丄偙偺偲偒偺愙揰偺嵗昗傪媮傔傛丅
乮俀乯丂倠偑 ![]() 亝倠亝
亝倠亝![]() 傪枮偨偟偰摦偔偲偒丄乮侾乯偱媮傔偨俀偮偺暯柺偺側偡妏兤偑偲傞抣
傪枮偨偟偰摦偔偲偒丄乮侾乯偱媮傔偨俀偮偺暯柺偺側偡妏兤偑偲傞抣
丂丂偺斖埻傪媮傔傛丅偨偩偟丄侽亝兤亝兾/俀 偲偡傞丅
乮夝乯乮侾乯丂倶2亄倷2亄乮倸亅侾乯2亖侾 傛傝丄拞怱偼丄乮侽丆侽丆侾乯偱丄敿宎偼侾偺媴偱偁傞丅
丂暯柺 倸亖侽 偼丄柧傜偐偵丄媮傔傞暯柺偺堦偮偱偁傞丅愙揰偼丄乮侽丆侽丆侽乯
丂傕偆堦偮偺愙暯柺 倎倶亄倐倷亄們倸亖倓 傪媮傔傛偆丅
丂捈慄 倶亄倷亅倠亖倸亖侽 偺曽岦儀僋僩儖偼丄乮侾丆亅侾丆侽乯偱丄乮倠丆侽丆侽乯丄乮侽丆倠丆侽乯傪捠傞丅
傛偭偰丄丂倎倠亖倐倠亖倓丂傛傝丄丂倎亖倐亖倓/倠
倎倶亄倐倷亄們倸亖倓 偵戙擖偟偰丄丂乮倓/倠乯倶亄乮倓/倠乯倷亄們倸亖倓丂懄偪丄丂倶亄倷亄乮倠們/倓乯倸亖倠
媴偺拞怱偐傜偺嫍棧偑敿宎侾偵摍偟偄偺偱丄乥乮倠們/倓乯亅倠乥/併乮侾亄侾亄乮倠們/倓乯2乯亖侾
偡側傢偪丄丂乥乮倠們/倓乯亅倠乥亖併乮侾亄侾亄乮倠們/倓乯2乯
椉曈傪暯曽偟偰丄丂乮倠們/倓乯2亅俀倠2乮們/倓乯亄倠2亖俀亄乮倠們/倓乯2丂傛傝丄俀倠2乮們/倓乯亖倠2亅俀
傛偭偰丄丂倠們/倓亖乮倠2亅俀乯/乮俀倠乯丂偲側傞偺偱丄媮傔傞愙暯柺偺曽掱幃偼丄
丂倶亄倷亄乮倠2亅俀乯/乮俀倠乯丒倸亖倠丂偡側傢偪丄丂俀倠倶亄俀倠倷亄乮倠2亅俀乯倸亖俀倠2
愙揰傪乮倶丆倷丆倸乯偲偍偔偲丄丂乮倶丆倷丆倸亅侾乯乤乮俀倠丆俀倠丆倠2亅俀乯丂傛傝丄倲 傪幚悢偲偟偰丄
丂倶亖俀倠倲丂丄倷亖俀倠倲丂丄倸亖侾亄乮倠2亅俀乯倲丂偲彂偗傞丅
丂倶2亄倷2亄乮倸亅侾乯2亖侾 側偺偱丄丂係倠2倲2亄係倠2倲2亄乮倠2亅俀乯2倲2亖侾
傛偭偰丄丂倲2亖侾/乮倠2亄俀乯2
偙偙偱丄倠亜侽丂傛傝丄丂倲亜侽丂偲偟偰傛偄偺偱丄丂倲亖侾/乮倠2亄俀乯
傛偭偰丄愙揰偺嵗昗偼丄丂乮俀倠/乮倠2亄俀乯丆俀倠/乮倠2亄俀乯丆侾亄乮倠2亅俀乯/乮倠2亄俀乯乯
偡側傢偪丄丂乮俀倠/乮倠2亄俀乯丆俀倠/乮倠2亄俀乯丆俀倠2/乮倠2亄俀乯乯
乮俀乯丂儀僋僩儖乮侽丆侽丆侾乯丄乮俀倠丆俀倠丆倠2亅俀乯偺側偡妏偑兤側偺偱丄
丂們倧倱兤亖乮倠2亅俀乯/乮倠2亄俀乯亖侾亅係/乮倠2亄俀乯
![]() 亝倠亝
亝倠亝![]() 傛傝丄丂係亝倠2亄俀亝俉丂側偺偱丄丂侽亝們倧倱兤亝侾/俀
傛傝丄丂係亝倠2亄俀亝俉丂側偺偱丄丂侽亝們倧倱兤亝侾/俀
侽亝兤亝兾/俀 傛傝丄丂兾/俁亝兤亝兾/俀丂丂乮廔乯
乮捛婰乯丂椷榓俈擭係寧侾係擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋侾乯偺栤戣偼丄慺杙側嬻娫恾宍偺栤戣偱偡偹丅
栤戣丂丂幚悢 倰 偵懳偟偰丄嬻娫偺揰(倰丆倰2丆倰3) 傪俹乮倰乯偱昞偡丅偝傜偵丄揰俹乮倰乯傪捠傝丄曽岦
丂丂儀僋僩儖偑(侾丆俀倰丆俁倰2)丄(侽丆俀丆俇倰)偱偁傞俀杮偺捈慄傪娷傓暯柺傪兾乮倰乯偱昞偡丅
丂丂倎倐們亗侽丄倎亗倐丄倎亗們 偱偁傞偲偒丄師偺栤偵摎偊傛丅
乮侾乯丂俁揰俹(侽)丄俹(倎)丄俹(倐乯傪捠傞暯柺兛偺曽掱幃傪媮傔傛丅
乮俀乯丂俁偮偺暯柺兾(侽)丄兾(倎)丄兾(們乯偺嫟桳揰俻偺嵗昗傪媮傔傛丅
乮俁乯丂兛偑俻傪捠傞偨傔偺昁梫廫暘忦審傪媮傔傛丅
乮夝乯乮侾乯丂俁揰俹(侽)丄俹(倎)丄俹(倐乯傪捠傞暯柺兛偺曽掱幃偼丄俙倶亄俛倷亄俠倸亖侽丂偲偍偗傞丅
偙偺偲偒丄丂俙倎亄俛倎2亄俠倎3亖侽丂丄俙倐亄俛倐2亄俠倐3亖侽丂偵偍偄偰丄倎亗侽丄倐亗侽丂傛傝丄
丂俙亄俛倎亄俠倎2亖侽丂丄俙亄俛倐亄俠倐2亖侽 傪曈乆堷偄偰丄丂俛乮倎亅倐乯亄俠乮倎2亅倐2乯亖侽
倎亗倐 傛傝丄丂俛亄俠乮倎亄倐乯亖侽丂側偺偱丄丂俛亖亅俠乮倎亄倐乯
偙偺偲偒丄丂俙亅俠倎乮倎亄倐乯亄俠倎2亖侽丂偐傜丄丂俙亖俠倎倐
傛偭偰丄暯柺兛偺曽掱幃偼丄俠倎倐倶亅俠乮倎亄倐乯倷亄俠倸亖侽丂懄偪丄倎倐倶亅乮倎亄倐乯倷亄倸亖侽
乮俀乯丂暯柺兾(侽) 偺曽掱幃偼丄乮侽丆侽丆侽乯傪捠傝丄曽岦儀僋僩儖偑(侾丆侽丆侽)丄(侽丆俀丆侽)偱偁
丂傞俀杮偺捈慄傪娷傓暯柺側偺偱丄丂倸亖侽丂偲側傞丅
丂暯柺兾(倎) 偺曽掱幃偼丄(倎丆倎2丆倎3)傪捠傝丄曽岦儀僋僩儖偑(侾丆俀倎丆俁倎2)丄(侽丆俀丆俇倎)偱偁
丂傞俀杮偺捈慄傪娷傓暯柺偱偁傞丅暯柺偺曽掱幃傪丂俙倶亄俛倷亄俠倸亖俢丂偲偍偔丅
偙偺偲偒丄丂俙倎亄俛倎2亄俠倎3亖俢丂丄俙亄俀倎俛亄俁倎2俠亖侽丂丄俀俛亄俇倎俠亖侽
俛亖亅俁倎俠丂傛傝丄丂俙亖俁倎2俠丂偲側傞丅偝傜偵丄丂俁倎3俠亅俁倎3俠亄俠倎3亖俢丂傛傝丄俢亖俠倎3
傛偭偰丄暯柺兾(倎) 偺曽掱幃偼丄俁倎2俠倶亅俁倎俠倷亄俠倸亖俠倎3丂懄偪丄俁倎2倶亅俁倎倷亄倸亖倎3
丂暯柺兾(們) 偺曽掱幃偼丄(們丆們2丆們3)傪捠傝丄曽岦儀僋僩儖偑(侾丆俀們丆俁們2)丄(侽丆俀丆俇們)偱偁
丂傞俀杮偺捈慄傪娷傓暯柺偱偁傞丅暯柺偺曽掱幃傪丂俙倶亄俛倷亄俠倸亖俢丂偲偍偔丅
偙偺偲偒丄丂俙們亄俛們2亄俠們3亖俢丂丄俙亄俀們俛亄俁們2俠亖侽丂丄俀俛亄俇們俠亖侽
俛亖亅俁們俠丂傛傝丄丂俙亖俁們2俠丂偲側傞丅偝傜偵丄丂俁們3俠亅俁們3俠亄俠們3亖俢丂傛傝丄俢亖俠們3
傛偭偰丄暯柺兾(們) 偺曽掱幃偼丄俁們2俠倶亅俁們俠倷亄俠倸亖俠們3丂懄偪丄俁們2倶亅俁們倷亄倸亖們3
俁偮偺暯柺兾(侽)丄兾(倎)丄兾(們乯偺嫟桳揰俻傪媮傔傞偨傔偵丄
丂倸亖侽丂傪戙擖偟偰丄丂俁倎2倶亅俁倎倷亖倎3丂偡側傢偪丄丂俁倎倶亅俁倷亖倎2
丂摨條偵丄俁們倶亅俁倷亖們2丂側偺偱丄倶亖乮倎亄們乯/俁丄倷亖倎們/俁丂傛傝丄俻乮乮倎亄們乯/俁丆倎們/俁丆侽乯
乮俁乯丂倎倐倶亅乮倎亄倐乯倷亄倸亖侽丂偑丄俻乮乮倎亄們乯/俁丆倎們/俁丆侽乯傪捠傞偺偱丄
丂倎倐乮倎亄們乯/俁亅乮倎亄倐乯倎們/俁亖侽丂偡側傢偪丄丂倎乮倐亅們乯亖侽丂傛傝丄丂倐亖們
傛偭偰丄兛偑俻傪捠傞偨傔偺昁梫廫暘忦審偼丄丂倐亖們丂丂乮廔乯
乮捛婰乯丂椷榓俈擭係寧侾俈擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋侾乯偺栤戣偼丄恀婾偺敾掕栤戣偱偁傞丅恀側傜偽徹柧丄婾
側傜偽斀椺傪偁偘傟偽傛偄丅
栤戣丂丂師偺俁偮偺柦戣偑惓偟偄偐偳偆偐傪挷傋傛丅
乮侾乯丂揰(倱倝値俀兤丆們倧倱俀兤丆俀們倧倱兤乯偼兤偺抣偵傛傜偢摨堦暯柺忋偵偁傞丅
乮俀乯丂揰(倱倝値俀兤丆們倧倱俀兤丆俀們倧倱兤乯偼兤偺抣偵傛傜偢摨堦媴柺忋偵偁傞丅
乮俁乯丂揰(倲丆倢倧倗2乮侾亄係倲乯丆倢倧倗2乮俀倲亄俀-倲乯乯偼 倲 偺抣偵傛傜偢摨堦暯柺忋偵偁傞丅
乮夝乯乮侾乯丂揰(倱倝値俀兤丆們倧倱俀兤丆俀們倧倱兤乯偑兤偺抣偵傛傜偢摨堦暯柺忋偵偁傞偲壖掕偟偰丄
偦偺暯柺偺曽掱幃傪丄丂倎倶亄倐倷亄們倸亖倓丂乮倎丄倐丄們 偺彮側偔偲傕侾偮偼侽偱側偄乯丂偲偍偔丅
丂偡側傢偪丄倎丒倱倝値俀兤亄倐丒們倧倱俀兤亄們丒俀們倧倱兤亖倓
兤亖侽丂偺偲偒丄丂倐亄俀們亖倓
兤亖兾/俀丂偺偲偒丄丂亅倐亖倓
兤亖兾丂偺偲偒丄丂倐亅俀們亖倓
兤亖兾/係丂偺偲偒丄丂倎亄![]() 們亖倓
們亖倓
傛偭偰丄丂倐亖亅倓丂丄們亖倓丂丄們亖亅倓丂偐傜丄丂倐亖們亖倓亖侽丂側偺偱丄丂倎亖侽
偙傟偼柕弬側偺偱丄摨堦暯柺忋偵偁傞偲偼尵偊側偄丅
乮俀乯丂兤亖侽丂偺偲偒丄(倱倝値俀兤丆們倧倱俀兤丆俀們倧倱兤乯亖乮侽丆侾丆俀乯
丂兤亖兾/俀丂偺偲偒丄(倱倝値俀兤丆們倧倱俀兤丆俀們倧倱兤乯亖乮侽丆亅侾丆侽乯
丂兤亖兾丂偺偲偒丄(倱倝値俀兤丆們倧倱俀兤丆俀們倧倱兤乯亖乮侽丆侾丆俀乯
偙偺俁揰偼丄乮侽丆侾丆侽乯傪拞怱偲偡傞敿宎俀偺墌廃忋偵偁傞丅
偦偙偱丄
丂乮倱倝値俀兤乯2亄乮們倧倱俀兤亅侾乯2亄乮俀們倧倱兤乯2
傪寁嶼偟偰傒傞丅揥奐偟偰丄
丂乮倱倝値俀兤乯2亄乮們倧倱俀兤亅侾乯2亄乮俀們倧倱兤乯2
亖係倱倝値2兤們倧倱2兤亄係倱倝値4兤亄係們倧倱2兤
亖係倱倝値2兤乮們倧倱2兤亄倱倝値2兤乯亄係們倧倱2兤亖係倱倝値2兤亄係們倧倱2兤亖係
傛偭偰丄揰(倱倝値俀兤丆們倧倱俀兤丆俀們倧倱兤乯偼兤偺抣偵傛傜偢丄拞怱乮侽丆侾丆侽乯偱敿宎俀偺媴柺
忋偵偁傞丅
乮俁乯丂倢倧倗2乮俀倲亄俀-倲乯亖倢倧倗2乮侾亄係倲乯亅倲丂側偺偱丄揰(倲丆倢倧倗2乮侾亄係倲乯丆倢倧倗2乮俀倲亄俀-倲乯乯偼
倲 偺抣偵傛傜偢暯柺 倸亖倷亅倶 偡側傢偪丄倶亅倷亄倸亖侽丂偺忋偵偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭係寧俀俉擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俀乯偺栤戣偼丄慺杙側嫍棧偺寁嶼偱偁傞丅
栤戣丂丂倶倷倸嬻娫偵偍偄偰丄倶倷暯柺偵揰(侽丆侾丆侽)傪拞怱偲偡傞敿宎侾偺墌俠1偲丄倷倸暯柺偵
丂丂揰(侽丆侽丆侽)傪拞怱偲偡傞敿宎侾偺墌俠2偑偁傞丅俠1忋偺揰俹偲俠2忋偺揰俻偑丄偦傟偧傟
丂丂揰(侽丆俀丆侽)丄(侽丆侽丆侾)傪弌敪揰偲偟偰俠1丄俠2忋傪惓偺岦偒偵摦偔丅揰俹偑揰俻偺俀攞偺
丂丂懍偝偱摦偔偲偒丄揰俹丄俻娫偺嫍棧偺嵟戝抣傪媮傔傛丅
丂丂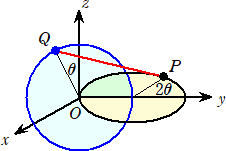
乮夝乯丂戣堄傛傝丄丂俹乮亅倱倝値俀兤丆侾亄們倧倱俀兤丆侽乯丄俻乮侽丆亅倱倝値兤丆們倧倱兤乯丂偲偍偗傞丅
傛偭偰丄
俹俻2亖倱倝値2俀兤亄乮侾亄們倧倱俀兤亄倱倝値兤乯2亄們倧倱2兤
亖係倱倝値2兤乮侾亅倱倝値2兤乯亄乮俀們倧倱2兤亄倱倝値兤乯2亄侾亅倱倝値2兤
亖俁倱倝値2兤亅係倱倝値4兤亄乮俀亅俀倱倝値2兤亄倱倝値兤乯2亄侾
亖俁倱倝値2兤亅係倱倝値4兤亄係亄係倱倝値4兤亄倱倝値2兤亅俉倱倝値2兤亅係倱倝値3兤亄係倱倝値兤亄侾
亖亅係倱倝値3兤亅係倱倝値2兤亄係倱倝値兤亄俆
丂倱倝値兤亖倶丂偲偍偔偲丄丂亅侾亝倶亝侾丂偱丄丂倷亖亅係倶3亅係倶2亄係倶亄俆丂偲偍偔丅
偙偺偲偒丄丂倷乫亖亅侾俀倶2亅俉倶亄係亖亅係乮倶亄侾乯乮俁倶亅侾乯亖侽丂傛傝丄丂倶亖亅侾丄侾/俁
丂倶亖侾/俁丂偺偲偒丄嬌戝偐偮嵟戝偱丄嵟戝抣丂侾俆俆/俀俈丂偲側傞丅
傛偭偰丄揰俹丄俻娫偺嫍棧偺嵟戝抣偼丄丂併乮侾俆俆/俀俈乯亖乮併係俇俆乯/俋丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俆寧俀俈擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋係乯偺栤戣偼丄戣堄偑偔傒庢傟傟偽暯堈側栤戣偱偁傞丅
栤戣丂丂尨揰傪俷偲偡傞嬻娫偵俁揰俙(倎丆侽丆侽)丄俛(侽丆倐丆侽)丄俠(侽丆侽丆們)傪偲傝丄巐柺懱俷俙俛俠
丂丂傪峫偊傞丅偨偩偟丄倎亜侽丄倐亜侽丄們亜侽 偲偡傞丅
乮侾乯丂俁揰俙丄俛丄俠傪捠傞暯柺偺曽掱幃丄偍傛傃丄尨揰偲偙偺暯柺偲偺嫍棧倛傪倎丄倐丄們偱昞偣丅
乮俀乯丂仮俙俛俠偺柺愊傪倎丄倐丄們偱昞偣丅
乮俁乯丂仮俙俛俠丄仮俷俙俛丄仮俷俛俠丄仮俷俠俙偺柺愊傪偦傟偧傟俽0丄俽1丄俽2丄俽3偲偟丄奺嶰妏宍
丂偺扨埵朄慄儀僋僩儖偱巐柺懱俷俙俛俠偺撪晹偐傜奜偵岦偐偆傕偺傪丄倳0丄倳1丄倳2丄倳3偲偡傞丅
丂儀僋僩儖俽0倳0亄俽2倳2亄俽3倳3 傪媮傔傛丅
乮夝乯乮侾乯丂俁揰俙丄俛丄俠傪捠傞暯柺偺曽掱幃偼丄丂倶/倎亄倷/倐亄倸/們亖侾丂側偺偱丄
丂倛亖侾/併乮侾/倎2亄侾/倐2亄侾/們2乯亖倎倐們/併乮倎2倐2亄倐2們2亄們2倎2乯
乮俀乯丂仮俙俛俠丒倛/俁亖倎倐/俀丒們/俁丂傛傝丄丂仮俙俛俠亖乮侾/俀乯併乮倎2倐2亄倐2們2亄們2倎2乯
乮俁乯丂倶/倎亄倷/倐亄倸/們亖侾丂傛傝丄倐們倶亄們倎倷亄倎倐倸亖倎倐們丂側偺偱丄
丂倳0亖乮倐們丆們倎丆倎倐乯/併乮倎2倐2亄倐2們2亄們2倎2乯
傛偭偰丄丂俽0倳0亖乮侾/俀乯乮倐們丆們倎丆倎倐乯
俽1亖倎倐/俀丂偱丄倳1亖乮侽丆侽丆亅侾乯丂傛傝丄丂俽1倳1亖乮侾/俀乯乮侽丆侽丆亅倎倐乯
俽2亖倐們/俀丂偱丄倳2亖乮亅侾丆侽丆侽乯丂傛傝丄丂俽2倳2亖乮侾/俀乯乮亅倐們丆侽丆侽乯
俽3亖們倎/俀丂偱丄倳3亖乮侽丆亅侾丆侽乯丂傛傝丄丂俽3倳3亖乮侾/俀乯乮侽丆亅們倎丆侽乯
傛偭偰丄丂俽0倳0亄俽2倳2亄俽3倳3亖乮侽丆侽丆侽乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧俈擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋係乯偺栤戣偼丄婎杮揑側栤戣偩傠偆丅
栤戣丂丂倶倷倸嬻娫偵偍偄偰丄
丂丂媴柺俽丗倶2亅俀倎倶亄倷2亄倸2亄倎2亅係亖侽偲暯柺兛丗倶亄俀倷亄倎倸亅侾亖侽
傪峫偊傞丅俽偲兛偑岎傢偭偰偱偒傞墌偺柺愊偑嵟彫偲側傞傛偆偵幚悢倎傪掕傔傛丅傑偨丄偦偺
偲偒偺墌偺拞怱偺嵗昗傪媮傔傛丅
乮夝乯丂媴柺俽丗乮倶亅倎乯2亄倷2亄倸2亖係 偺拞怱俠乮倎丆侽丆侽乯丄敿宎俀 偱偁傞丅
俠乮倎丆侽丆侽乯偲暯柺兛丗倶亄俀倷亄倎倸亅侾亖侽 偺嫍棧偼丄乥倎亅侾乥/併乮倎2亄俆乯 側偺偱丄
墌偺敿宎傪 倰 偲偡傞偲丄
丂倰2亖係亅乮倎亅侾乯2/乮倎2亄俆乯亖乮俁倎2亄俀倎亄侾俋乯/乮倎2亄俆乯亖俁亄乮俀倎亄係乯/乮倎2亄俆乯
丂倷亖乮俀倎亄係乯/乮倎2亄俆乯 偑嵟彫偲側傞 倎 傪媮傔傞丅
丂倷乫亖亅俀乮倎亄俆乯乮倎亅侾乯/乮倎2亄俆乯2
丂倎仺亇亣丂偺偲偒丄倷仺侽丂側偺偱丄倷偼丄倎亖亅俆偺偲偒丄嬌彫偐偮嵟彫偲側傞丅
偙偺偲偒丄俠乮亅俆丆侽丆侽乯偐傜暯柺兛丗倶亄俀倷亅俆倸亅侾亖侽偵壓傠偟偨悅慄偺懌偑媮傔傞墌偺
拞怱偲側傞丅乮亅俆丆侽丆侽乯傪捠傝丄儀僋僩儖乮侾丆俀丆亅俆乯偵暯峴側捈慄偺曽掱幃偼丄
丂倶亄俆亖倷/俀亖倸/亅俆丂偲彂偗傞丅偡側傢偪丄幚悢傪 倲 偲偟偰丄丂倶亖倲亅俆丄倷亖俀倲丄倸亖亅俆倲
暯柺偺曽掱幃偵戙擖偟偰丄丂倲亅俆亄俀乮俀倲乯亅俆乮亅俆倲乯亅侾亖侽丂偡側傢偪丄丂倲亖侾/俆
丂媮傔傞墌偺拞怱偺嵗昗偼丄丂乮亅俀係/俆丆俀/俆丆亅侾乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧侾俈擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俆乯偺栤戣傕丄婎杮揑側栤戣偩傠偆丅
栤戣丂丂俽傪曽掱幃 倶2亄倷2亄倸2亖俆 偺掕傔傞媴柺偲偡傞丅
乮侾乯丂俽忋偺侾揰俹偵偍偗傞愙暯柺傪峫偊傞丅尨揰俷丄愙暯柺忋偺揰俻偵懳偟丄撪愊俷俹丒俷俻
丂丂傪媮傔傛丅
乮俀乯丂俽忋偺俀揰俹1乮俀丆侽丆侾乯丄俹2乮侽丆俀丆侾乯偺偦傟偧傟偵偍偗傞愙暯柺傪峫偊傞丅椉曽偺愙
丂丂暯柺偵娷傑傟傞揰偺偆偪丄尨揰俷偐傜偺嫍棧偑嵟彫偱偁傞揰俼傪媮傔傛丅
乮夝乯乮侾乯丂俷俹丒俷俻亖俷俹丒乮俷俹亄俹俻乯亖俷俹丒俷俹亄俷俹丒俹俻乯亖乥俷俹乥2亖俆
乮俀乯丂俀揰俹1乮俀丆侽丆侾乯丄俹2乮侽丆俀丆侾乯偺偦傟偧傟偵偍偗傞愙暯柺偺曽掱幃偼丄乮侾乯傛傝丄
丂俀乮倶亅俀乯亄侽乮倷亅侽乯亄倸亅侾亖侽丂偡側傢偪丄丂俀倶亄倸亖俆
丂侽乮倶亅侽乯亄俀乮倷亅俀乯亄倸亅侾亖侽丂偡側傢偪丄丂俀倷亄倸亖俆丂傛傝丄丂倶亖倷丂丄倸亖俆亅倶
丂傛偭偰丄俀偮偺愙暯柺偺岎慄忋偺揰俼偺嵗昗偼丄俼乮倲丆倲丆俆亅倲乯丂偲彂偗傞丅
偙偺偲偒丄丂乥俷俼乥2亖倲2亄倲2亄乮俆亅倲乯2亖俁倲2亅侾侽倲亄俀俆丂偐傜丄
丂俇倲亅侾侽亖丂偡側傢偪丄丂倲亖俆/俁丂偺偲偒丄乥俷俼乥偼嵟彫偲側傞丅
丂傛偭偰丄丂俼乮俆/俁丆俆/俁丆俆/俁乯丂偱偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧俀侾擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俆乯偺栤戣偼丄暯柺偵傛傞媴柺偺愗傝岥偺栤戣偱偁傞丅
栤戣丂丂嬻娫偵俁揰俙乮![]() 丆
丆![]() 丆侽乯丄俛乮侾丆亅侾丆
丆侽乯丄俛乮侾丆亅侾丆![]() 乯丄俠乮亅侾丆侾丆
乯丄俠乮亅侾丆侾丆![]() 乯偑梌偊傜傟偰偄傞丅
乯偑梌偊傜傟偰偄傞丅
乮侾乯丂儀僋僩儖俙俛偲俙俠偺側偡妏傪媮傔傛丅
乮俀乯丂俁揰俙丄俛丄俠傪捠傞暯柺俽偺曽掱幃傪媮傔傛丅
乮俁乯丂尨揰俷傪捠傞媴柺偱丄暯柺俽偵傛傞愗傝岥偑仮俙俛俠偺撪愙墌偲側傞傕偺偺曽掱幃傪媮
丂丂傔傛丅
乮夝乯乮侾乯丂俙俛亖乮侾亅![]() 丆亅侾亅
丆亅侾亅![]() 丆
丆![]() 乯丄俙俠亖乮亅侾亅
乯丄俙俠亖乮亅侾亅![]() 丆侾亅
丆侾亅![]() 丆
丆![]() 乯傛傝丄
乯傛傝丄
丂俙俛亖併乷乮侾亅![]() 乯2亄乮侾亄
乯2亄乮侾亄![]() 乯2亄俀乸亖俀
乯2亄俀乸亖俀![]()
丂俙俠亖併乷乮侾亄![]() 乯2亄乮侾亅
乯2亄乮侾亅![]() 乯2亄俀乸亖俀
乯2亄俀乸亖俀![]()
丂俙俛丒俙俠亖亅侾亄俀亅侾亄俀亄俀亖係丂側偺偱丄儀僋僩儖俙俛偲俙俠偺側偡妏傪兤偲偡傞偲丄
丂們倧倱兤亖係/乮俀![]() 丒俀
丒俀![]() 乯亖侾/俀丂傛傝丄丂兤亖兾/俁
乯亖侾/俀丂傛傝丄丂兤亖兾/俁
乮俀乯丂暯柺俽偺朄慄儀僋僩儖傪 値亖乮倎丆倐丆們乯偲偍偔偲丄値佦俙俛丄値佦俙俠丂偐傜丄
丂倎乮侾亅![]() 乯亅倐乮侾亄
乯亅倐乮侾亄![]() 乯亄們
乯亄們![]() 亖侽丂丄亅倎乮侾亄
亖侽丂丄亅倎乮侾亄![]() 乯亄倐乮侾亅
乯亄倐乮侾亅![]() 乯亄們
乯亄們![]() 亖侽
亖侽
曈乆堷偄偰丄丂俀倎亅俀倐亖侽丂偡側傢偪丄丂倎亖倐丂偱丄偙偺偲偒丄丂們亖俀倎
傛偭偰丄暯柺偺曽掱幃偼丄丂倎乮倶亅![]() 乯亄倎乮倷亅
乯亄倎乮倷亅![]() 乯亄俀倎倸亖侽丂偐傜丄
乯亄俀倎倸亖侽丂偐傜丄
丂倶亄倷亄俀倸亖俀![]() 丂偲側傞丅
丂偲側傞丅
乮俁乯丂乮侾乯傛傝丄仮俙俛俠偼惓嶰妏宍偱丄偦偺撪愙墌偺拞怱偼丄仮俙俛俠偺廳怱偵摍偟偄丅
丂傛偭偰丄拞怱偺嵗昗偼丄丂乮![]() /俁丆
/俁丆![]() /俁丆俀
/俁丆俀![]() /俁乯丂偲側傞丅
/俁乯丂偲側傞丅
媮傔傞媴柺偺拞怱傪 乮倱丆倲丆倳乯 偲偍偔偲丄
丂乮倱亅![]() /俁丆倲亅
/俁丆倲亅![]() /俁丆倳亅俀
/俁丆倳亅俀![]() /俁乯亖倠乮侾丆侾丆俀乯
/俁乯亖倠乮侾丆侾丆俀乯
偐傜丄丂倱亖倠亄![]() /俁丂丄倲亖倠亄
/俁丂丄倲亖倠亄![]() /俁丂丄倳亖俀倠亄俀
/俁丂丄倳亖俀倠亄俀![]() /俁
/俁
偙偙偱丄曈俛俠偺拞揰偼丄乮侽丆侽丆![]() 乯丂偱丄戣堄傛傝丄
乯丂偱丄戣堄傛傝丄
乮倠亄![]() /俁乯2亄乮倠亄
/俁乯2亄乮倠亄![]() /俁乯2亄乮俀倠亅
/俁乯2亄乮俀倠亅![]() /俁乯2亖乮倠亄
/俁乯2亖乮倠亄![]() /俁乯2亄乮倠亄
/俁乯2亄乮倠亄![]() /俁乯2亄乮俀倠亄俀
/俁乯2亄乮俀倠亄俀![]() /俁乯2
/俁乯2
偑惉傝棫偮偺偱丄丂係倠2亅係乮![]() /俁乯倠亄俀/俋亖係倠2亄俉乮
/俁乯倠亄俀/俋亖係倠2亄俉乮![]() /俁乯倠亄俉/俋丂傛傝丄
/俁乯倠亄俉/俋丂傛傝丄
丂倠亖亅![]() /侾俀丂偲側傞丅傛偭偰丄媴柺偺拞怱偺嵗昗偼丄乮
/侾俀丂偲側傞丅傛偭偰丄媴柺偺拞怱偺嵗昗偼丄乮![]() /係丆
/係丆![]() /係丆
/係丆![]() /俀乯丂偲側傝丄
/俀乯丂偲側傝丄
媴柺偺敿宎偼丄丂併乷乮![]() /係乯2亄乮
/係乯2亄乮![]() /係乯2亄乮
/係乯2亄乮![]() /俀乯2乸亖
/俀乯2乸亖![]() /俀丂偱偁傞丅
/俀丂偱偁傞丅
埲忋偐傜丄媮傔傞媴柺偺曽掱幃偼丄
丂乮倶亅![]() /係乯2亄乮倷亅
/係乯2亄乮倷亅![]() /係乯2亄乮倸亅
/係乯2亄乮倸亅![]() /俀乯2亖俁/係丂丂乮廔乯
/俀乯2亖俁/係丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧俀俈擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俆乯偺栤戣偼丄嬻娫偵偍偗傞婎杮栤戣偱偁傞丅
栤戣丂丂嬻娫偵係揰俙乮係丆侽丆侽乯丄俛乮侽丆侽丆俀乯丄俠乮侽丆侾丆係乯丄俢乮俁丆俉丆俁乯偑偁傞丅
乮侾乯丂仮俙俛俠偺柺愊傪媮傔傛丅
乮俀乯丂俁揰俙丄俛丄俠傪捠傞暯柺偺曽掱幃傪媮傔傛丅
乮俁乯丂巐柺懱俙俛俠俢偺懱愊傪媮傔傛丅
乮夝乯乮侾乯丂俙俛亖乮亅係丆侽丆俀乯丄俙俠亖乮亅係丆侾丆係乯丂偐傜丄俙俛2亖俀侽丂丄俙俠2亖俁俁
丂俙俛丒俙俠亖俀係丂側偺偱丄丂仮俙俛俠亖乮侾/俀乯併乮俀侽亊俁俁亅俀係2乯亖併俀侾
乮俀乯丂倎倶亄倐倷亄們倸亖倓丂偵偍偄偰丄丂係倎亖倓丄俀們亖倓丄倐亄係們亖倓丂傛傝丄
丂倎亖倓/係丄們亖倓/俀丄倐亖亅倓丂側偺偱丄媮傔傞暯柺偺曽掱幃偼丄
丂乮侾/係乯倶亅倷亄乮侾/俀乯倸亖侾丂偡側傢偪丄丂倶亅係倷亄俀倸亖係
乮俁乯丂俢傛傝丄暯柺 倶亅係倷亄俀倸亖係 偵壓傠偟偨悅慄偺挿偝偼丄
丂乥俁亅俁俀亄俇亅係乥/併俀侾亖俀俈/併俀侾
傛偭偰丄巐柺懱俙俛俠俢偺懱愊偼丄丂併俀侾亊乮俀俈/併俀侾乯亊乮侾/俁乯亖俋丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俈寧俆擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋俇乯偺栤戣偼丄夝偄偰偄偰妝偟偄栤戣偱偁傞丅
栤戣丂丂揰乮俈丆俇丆係乯傪拞怱偲偡傞敿宎俁偺媴偑偁傝丄偦偺昞柺偼嬀偱偱偒偰偄傞傕偺偲偡傞丅
丂丂偄傑丄曽岦儀僋僩儖乮俁丆俀丆侾乯傪傕偮岝偑尨揰偐傜敪幩偝傟偨偲偡傞丅偙偺岝偼媴柺偺偳偺
丂丂揰偱斀幩偟丄倶倷 暯柺偲偳偺揰偱岎傢傞偐丅偨偩偟丄媴柺偱偺岝偺斀幩偼丄偦偺揰偱偺朄慄
丂丂偲擖幩岝慄傪娷傓暯柺撪偱婲偙傝丄擖幩妏偲斀幩妏偼摍偟偄偲偡傞丅
乮夝乯丂尨揰偼丄揰乮俈丆俇丆係乯傪拞怱偲偡傞敿宎俁偺媴偺奜懁偵偁傞丅曽岦儀僋僩儖乮俁丆俀丆侾乯
傪傕偮岝偑尨揰偐傜敪幩偝傟偨偲偒丄偦偺岝慄忋偺揰偼丄倠乮俁丆俀丆侾乯偲昞偝傟傞丅
偙偺岝慄偲丄揰乮俈丆俇丆係乯傪拞怱偲偡傞敿宎俁偺媴柺偲偺岎揰偼丄
丂乮俁倠亅俈乯2亄乮俀倠亅俇乯2亄乮倠亅係乯2亖俋丂偐傜丄倠亖俀丄俀俁/俈
丂俀俁/俈亜俀丂傛傝岝慄偑媴柺偲嵟弶偵岎傢傞偺偼丄丂倠亖俀丂偺応崌偱偁傞丅
丂偟偨偑偭偰丄岝慄偼丄媴柺偲丄丂揰乮俇丆係丆俀乯丂偱斀幩偡傞丅
丂偙偺偲偒丄媴柺偺拞怱乮俈丆俇丆係乯偐傜斀幩揰乮俇丆係丆俀乯偵岦偐偆儀僋僩儖偼丄
乮亅侾丆亅俀丆亅俀乯丂偱丄戝偒偝偑俁偱偁傞偙偲偐傜丄摨偠岦偒偺扨埵儀僋僩儖偼丄
乮亅侾/俁丆亅俀/俁丆亅俀/俁乯丂偲側傞丅
傛偭偰丄乮亅俇丆亅係丆亅俀乯傪乮亅侾/俁丆亅俀/俁丆亅俀/俁乯偵娭偟偰嬀塮曄姺偝偣傞偲丄
乮亅俇丆亅係丆亅俀乯亅乷乮亅俇丆亅係丆亅俀乯丒乮亅侾/俁丆亅俀/俁丆亅俀/俁乯乸乮亅侾/俁丆亅俀/俁丆亅俀/俁乯
亖乮亅係丆侽丆俀乯丂偐傜丄
乮亅俇丆亅係丆亅俀乯亅俀乮亅係丆侽丆俀乯亖乮俀丆亅係丆亅俇乯
傛偭偰丄乮俇丆係丆俀乯傪捠傝丄曽岦儀僋僩儖偑乮俀丆亅係丆亅俇乯偺捈慄偺曽掱幃偼丄
丂乮倶亅俇乯/俀亖乮倷亅係乯/乮亅係乯亖乮倸亅俀乯/乮亅俇乯
偙偺偲偒丄倶倷暯柺偲偺岎揰偼丄倸亖侽丂傪戙擖偟偰丄倶亖俀侽/俁丂丄倷亖俉/俁
埲忋偐傜丄媮傔傞揰偺嵗昗偼丄丂乮俀侽/俁丆俉/俁丆侽乯
乮捛婰乯丂椷榓俈擭俈寧俉擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俇乯偺栤戣偼丄婎杮栤戣偩傠偆丅
栤戣丂丂媴柺俽丗乮倶亅俁乯2亄(倷亅俀乯2亄乮倸亅侾乯2亖侾 偲揰俹乮亅侾丆俇丆俁乯偑梌偊傜傟偰偄傞丅
丂丂揰俹傪捠傝媴柺俽偵愙偡傞偡傋偰偺捈慄偐傜側傞恾宍偲俽偲偺嫟捠晹暘偲偟偰掕傑傞墌傪
丂丂俠偲偡傞丅墌俠偺拞怱俙偺嵗昗偍傛傃敿宎 倰 傪媮傔傛丅傑偨丄墌俠傪娷傓暯柺兛偺曽掱幃
丂丂傪媮傔傛丅
乮夝乯丂愙揰傪乮倶丆倷丆倸乯偲偍偔偲丄丂乮倶亅俁丆倷亅俀丆倸亅侾乯丒乮倶亄侾丆倷亅俇丆倸亅俁乯亖侽丂偐傜丄
丂乮倶亅俁乯乮倶亄侾乯亄乮倷亅俀乯乮倷亅俇乯亄乮倸亅侾乯乮倸亅俁乯亖侽
偡側傢偪丄丂倶2亄倷2亄倸2亅俀倶亅俉倷亅係倸亄侾俀亖侽
媴柺俽丗倶2亄倷2亄倸2亅俇倶亅係倷亅俀倸亄侾俁亖侽丂偲楢棫偟偰丄丂係倶亅係倷亅俀倸亅侾亖侽
偙傟偑丄暯柺兛偺曽掱幃偱偁傞丅
揰俹偲媴偺拞怱偲偺嫍棧偼丄丂併乷乮亅係乯2亄係2亄俀2乸亖俇丂偱丄媴偺敿宎 侾 偱偁傞偙偲偐傜丄
愙慄偺挿偝偼丄丂併乮俇2亅侾乯亖併俁俆丂偲側傞丅
揰俹偲暯柺兛偺嫍棧偼丄丂乥亅係亅俀係亅俇亅侾乥/俇亖俁俆/俇丂側偺偱丄墌俠偺敿宎 倰 偼丄
丂 倰 亖併乮俁俆亅乮俁俆/俇乯2乯亖乮併俁俆乯/俇
墌俠偺拞怱俙偺嵗昗傪乮倶丆倷丆倸乯偲偍偔偲丄捈慄俙俹偺曽掱幃偼丄
丂乮倶亄侾乯/俀亖乮倷亅俇乯/乮亅俀乯亖乮倸亅俁乯/乮亅侾乯
傛偭偰丄丂倶亖俀倲亅侾丄倷亖亅俀倲亄俇丄倸亖亅倲亄俁丂偲彂偗傞丅
傛偭偰丄丂係乮俀倲亅侾乯亅係乮亅俀倲亄俇乯亅俀乮亅倲亄俁乯亅侾亖侽丂傛傝丄倲亖俁俆/侾俉丂側偺偱丄
墌俠偺拞怱俙偺嵗昗偼丄丂乮俀俇/俋丆侾俋/俋丆侾俋/侾俉乯丂偲側傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俈寧侾俁擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俇乯偺栤戣偼丄嵟屻偺傑偲傔曽偑擄偟偄丅
栤戣丂丂揰俷(侽丆侽丆侽)丄俙(俀丆侽丆侽)丄俛(侽丆係丆侽)丄俠(侽丆侽丆係)傪捀揰偲偡傞巐柺懱V偲
丂丂暯柺兛丗倶亄俀倷亄俀倸亖俀倠 偑偁傞丄倁偼丄兛偲岎傢傝丄偦偺愗傝岥偼巐妏宍偱偁傞偲偡傞丅
丂丂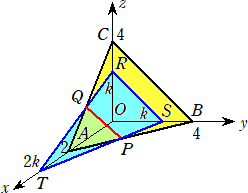
乮侾乯丂倠偺斖埻傪媮傔傛丅
乮俀乯丂愗傝岥偺巐妏宍偺柺愊傪倠偱昞偣丅
乮俁乯丂倁傪兛偵傛傝俀偮偺晹暘偵愗抐偟丄捀揰俷傪娷傓晹暘傪倂偲偡傞丅俁偮偺嵗昗暯柺偵愙
丂丂偟丄倂偵娷傑傟傞媴偺敿宎偺嵟戝抣傪媮傔傛丅
乮夝乯乮侾乯丂暯柺兛丗倶亄俀倷亄俀倸亖俀倠 偼丄奺幉偲丄乮俀倠丆侽丆侽乯丄乮侽丆倠丆侽乯丄乮侽丆侽丆倠乯 偱
丂岎傢傞丅
丂傑偨丄暯柺俙俛俠偺曽掱幃偼丄丂倶/俀亄倷/係亄倸/係亖侾丂偡側傢偪丄丂俀倶亄倷亄倸亖係
丂乮俀倠丆侽丆侽乯偲乮侽丆倠丆侽乯傪寢傇捈慄偲捈慄俙俛偺岎揰偼丄倶亄俀倷亖俀倠丂丄俀倶亄倷亖係丂傪
楢棫偟偰丄丂倶亖乮俉亅俀倠乯/俁丂丄倷亖係乮倠亅侾乯/俁
戣堄傛傝丄丂侽亙乮俉亅俀倠乯/俁亙俀丂側偺偱丄丂侾亙倠亙係
乮俀乯丂俿俽亖![]() 倠丂偱丄俿俹亖係
倠丂偱丄俿俹亖係![]() 乮倠亅侾乯/俁丂傛傝丄丂俿俽 丗 俿俹亖俁倠 丗 係乮倠亅侾乯
乮倠亅侾乯/俁丂傛傝丄丂俿俽 丗 俿俹亖俁倠 丗 係乮倠亅侾乯
丂仮俿俼俽偼俀摍曈嶰妏宍偱丄偦偺崅偝偼丄丂併乮俆倠2亅倠2/俀乯亖俁倠/![]() 丂傛傝丄
丂傛傝丄
丂仮俿俼俽亖![]() 倠丒乮俁倠/
倠丒乮俁倠/![]() 乯丒乮侾/俀乯亖俁倠2/俀
乯丒乮侾/俀乯亖俁倠2/俀
丂仮俿俼俽佷仮俿俻俹丂傛傝丄丂仮俿俼俽 丗 仮俿俻俹亖俋倠2 丗 侾俇乮倠亅侾乯2丂側偺偱丄
丂俋倠2丒仮俿俻俹亖侾俇乮倠亅侾乯2丒仮俿俼俽亖俀係倠2乮倠亅侾乯2
傛偭偰丄丂仮俿俻俹亖俉乮倠亅侾乯2/俁丂偲側傝丄
巐妏宍俹俻俼俽亖俁倠2/俀亅俉乮倠亅侾乯2/俁亖乮亅俈倠2亄俁俀倠亅侾俇乯/俇
乮俁乯丂倂偵娷傑傟傞媴偺拞怱偼丄戣堄傛傝丄乮倰丆倰丆倰乯偲偍偗傞丅
丂拞怱偼丄暯柺兛偲暯柺俙俛俠偵娭偟偰丄尨揰偲摨偠懁偵偁傞偺偱丄
丂俀倶亄倷亄倸亙係丂偐傜丄丂係倰亙係丂偡側傢偪丄丂倰亙侾
丂傛偭偰丄丂倶亄俀倷亄俀倸亙俀倠丂偐傜丄丂俆倰亙俀倠丂偡側傢偪丄丂倰亙乮俀/俆乯倠
媴柺偑暯柺兛偵愙偡傞偲偒丄丂乮亅俆倰亄俀倠乯/俁亖倰丂偐傜丄丂倰亖倠/係
媴柺偑暯柺俙俛俠偵愙偡傞偲偒丄丂乮亅係倰亄係乯/![]() 亖倰丂偐傜丄丂倰亖俀乮係亅
亖倰丂偐傜丄丂倰亖俀乮係亅![]() 乯/俆丂丂乮廔乯
乯/俆丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俈寧侾俉擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋俈乯偺栤戣偼丄婎杮栤戣偱偁傞丅
栤戣丂丂嬻娫偺俀掕揰俷乮侽丆侽丆侽乯丄俙乮亅侾丆侾丆侾乯偵懳偟丄揰俹乮倶丆倷丆倸乯偼師偺俀忦審乮鶣乯丄
丂丂乮鶤乯傪枮偨偟側偑傜摦偔偲偡傞丅
乮鶣乯丂揰俹偼丄曽掱幃 倷亖俀倶 偱梌偊傜傟傞暯柺忋偵偁傞丅
乮鶤乯丂儀僋僩儖俷俙偲儀僋僩儖俙俹偼悅捈偱偁傞丅
丂偙偺偲偒丄儀僋僩儖俙俹偺挿偝偺嵟彫抣偲丄偦偺嵟彫抣傪梌偊傞俹偺嵗昗乮倶丆倷丆倸乯傪媮傔傛丅
乮夝乯丂戣堄傛傝丄俹乮倶丆俀倶丆倸乯偲偍偗傞丅偙偺偲偒丄丂俙俹亖乮倶亄侾丆俀倶亅侾丆倸亅侾乯丂偱偁傞丅
丂俷俙佦俙俹丂傛傝丄丂俷俙丒俙俹亖亅乮倶亄侾乯亄俀倶亅侾亄倸亅侾亖倶亅俁亄倸亖侽丂側偺偱丄
丂倸亖俁亅倶丂偲側傞丅偡側傢偪丄丂俙俹亖乮倶亄侾丆俀倶亅侾丆俀亅倶乯
偙偺偲偒丄
丂乥俙俹乥2亖乮倶亄侾乯2亄乮俀倶亅侾乯2亄乮俀亅倶乯2亖俇倶2亅俇倶亄俇亖俇乮倶亅侾/俀乯2亄俋/俀
偐傜丄儀僋僩儖俙俹偺挿偝偼丄倶亖侾/俀 偺偲偒嵟彫偱丄嵟彫抣偼丄丂併乮俋/俀乯亖乮俁/俀乯![]()
偙偺偲偒偺俹偺嵗昗偼丄丂乮侾/俀丆侾丆俆/俀乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俈寧俁侽擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俈乯偺栤戣偼丄婎杮栤戣偱偁傞丅
栤戣丂丂嬻娫撪偺揰俙乮侾丆侾丆侽乯偲俛乮亅侾丆亅俀丆侾乯傪捠傞捈慄傪俴偲偡傞丅俹偑俴忋傪摦偔偲
丂丂偒丄俹偲 倶 幉偺嫍棧偺嵟彫抣倓傪媮傔傛丅
乮夝乯丂捈慄俴偺曽掱幃偼丄丂乮倶亅侾乯/俀亖乮倷亅侾乯/俁亖亅倸丂側偺偱丄俴忋偺揰俹偺嵗昗偼丄
丂俹乮俀倲亄侾丆俁倲亄侾丆亅倲乯丂偲偍偗傞丅倶 幉忋偺揰俻偺嵗昗偼丄丂俻乮倱丆侽丆侽乯丂偲偍偗傞丅
偙偺偲偒丄俻俹亖乮俀倲亄侾亅倱丆俁倲亄侾丆亅倲乯丂偱丄俻俹佦乮俀丆俁丆亅侾乯丄俻俹佦乮侾丆侽丆侽乯丂傛傝丄
丂俀乮俀倲亄侾亅倱乯亄俁乮俁倲亄侾乯亄倲亖侽丂丄俀倲亄侾亅倱亖侽
偡側傢偪丄丂侾係倲亅俀倱亄俆亖侽丂丄俀倲亄侾亅倱亖侽丂偐傜丄丂侾侽倲亖亅俁丂傛傝丄丂倲亖亅俁/侾侽
偙偺偲偒丄丂倱亖俀/俆丂側偺偱丄丂俻俹亖乮侽丆侾/侾侽丆俁/侾侽乯
傛偭偰丄丂倓亖併乮侾/侾侽侽亄俋/侾侽侽乯亖侾/![]() 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧1擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俉乯偺栤戣偼丄摢偺拞偱恾宍傪僀儊乕僕偟側偑傜峫偊傞栤戣
偱偁傞丅
栤戣丂丂嬻娫偵偍偄偰丄俀揰俹乮亅倲丆亅侾丆倲2亅侾乯丄俻乮倲丆侾丆乮倕倲亄倕-倲乯/俀亅乮倕亄倕-1乯/俀乯傪
丂丂峫偊傞丅偨偩偟丄乥倲乥亝侾偲偡傞丅侽亙倳亙侾偱偁傞倳偵懳偟偰慄暘俹俻偲暯柺 倷亖倳 偲偺岎
丂丂揰傪俼乮倶丆倷丆倸乯偲偡傞丅
乮侾乯丂倲 傪亅侾偐傜侾傑偱摦偐偡偲偒丄倶 偺摦偔斖埻傪倳偱昞偣丅
乮俀乯丂俼偺倸嵗昗傪 倶 偲 倳 偺幃偱昞偣丅
乮俁乯丂倲 傪亅侾偐傜侾傑偱摦偐偡偲偒丄慄暘俹俻偑摦偄偰偱偒傞恾宍偲俀暯柺 倷亖侾丄倸亖侽 偲偱
丂丂埻傑傟傞晹暘偺懱愊傪媮傔傛丅
乮夝乯乮侾乯丂戣堄傛傝丄嶲峫恾傪恾帵偡傞偲丄
丂丂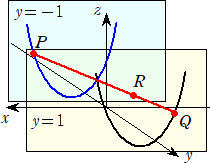
丂慄暘俹俻偵偍偄偰丄揰俼偼丄値丗侾亅値 偵撪暘偡傞揰側偺偱丄俷傪嵗昗幉偺尨揰偲偟偰丄
丂俷俼亖乮侾亅値乯俷俹亄値俷俻丂偵偍偄偰丄倷亖値亅侾亄値亖俀値亅侾亖倳丂傛傝丄値亖乮倳亄侾乯/俀
偙偺偲偒丄丂倶亖乮値亅侾乯倲亄値倲亖乮俀値亅侾乯倲亖倳倲丂偱丄丂亅侾亝倲亝侾丂傛傝丄丂亅倳亝倶亝倳
乮俀乯丂倸亖乮侾亅値乯乮倲2亅侾乯亄値乮乮倕倲亄倕-倲乯/俀亅乮倕亄倕-1乯/俀乯
丂亖乮乮侾亅倳乯/俀乯乮倲2亅侾乯亄乮乮倳亄侾乯/俀乯乮乮倕倲亄倕-倲乯/俀亅乮倕亄倕-1乯/俀乯
偝傜偵丄丂倲亖倶/倳 傪戙擖偟偰丄
丂倸亖乮乮侾亅倳乯/俀乯乮乮倶/倳乯2亅侾乯亄乮乮倳亄侾乯/係乯乮倕x/u亄倕-x/u亅倕亅倕-1乯
乮俁乯丂乮俀乯傛傝丄丂倶亖亇倳丂偺偲偒丄丂倸亖侽丂偱丄亅倳亙倶亙倳丂偺偲偒丄丂倸亙侽丂偱偁傞丅
丂嬋柺傪 倷亖倳 偱愗偭偨愗傝岥偱丄倸亝侽 偱偁傞晹暘偺柺愊偼丄
佺-uu 乮亅倸乯倓倶亖俀佺0u 乮乮乮倳亅侾乯/俀乯乮乮倶/倳乯2亅侾乯亅乮乮倳亄侾乯/係乯乮倕x/u亄倕-x/u亅倕亅倕-1乯乯倓倶
亖俀[乮乮倳亅侾乯/俀乯乮乮倶3/乮俁倳2乯亅倶乯亅乮乮倳亄侾乯/係乯乮倳倕x/u亅倳倕-x/u亅乮倕亄倕-1乯倶乯]0u
亖乮倳亅侾乯乮倳/俁亅倳乯亄乮倳亄侾乯倳倕-1
亖俀倳乮侾亅倳乯/俁亄乮倳亄侾乯倳倕-1
偟偨偑偭偰丄媮傔傞懱愊偼丄
丂佺01 乮俀倳乮侾亅倳乯/俁亄乮倳亄侾乯倳倕-1乯倓倳
亖[倳2/俁亅俀倳3/俋亄乮倳3/俁亄倳2/俀乯倕-1乯]01
亖侾/俁亅俀/俋亄乮侾/俁亄侾/俀乯倕-1亖侾/俋亄乮俆/俇乯倕-1丂丂乮廔乯
乮僐儊儞僩乯丂僴乕僪側寁嶼偱偟偨丅杮斣偱帪娫撪偵夝偒偒傞帺怣偼慡偔偁傝傑偣傫丅
乮捛婰乯丂椷榓俈擭俋寧係擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俉乯偺栤戣偼丄婎杮栤戣偩傠偆丅
栤戣丂丂嬻娫偵係揰俷丄俙丄俛丄俠 偑偁傝丄俷俙亖乮俀丆俀丆俀乯丄俷俛亖乮倎丆亅俀丆侾乯丄
丂丂俷俠亖乮倶丆倷丆倸乯偲偡傞丅 俷俠偼俷俙偍傛傃俷俛偲捈岎偟丄俷俠偺戝偒偝偼俴偱偁傞丅傑偨丄
丂丂俙俠偲俛俠偼捈岎偡傞丅
乮侾乯丂俴傪 倎 偱昞偣丅
乮俀乯丂俴亖侾偑惉傝棫偮偲偒偺俷俠傪媮傔傛丅
乮夝乯乮侾乯丂俙俠偲俛俠偼捈岎偡傞偺偱丄丂俙俠丒俛俠亖侽丂懄偪丄乮俷俠亅俷俙乯丒乮俷俠亅俷俛乯亖侽
丂俷俠偼俷俙偍傛傃俷俛偲捈岎偡傞偺偱丄丂俷俠丒俷俙亖侽丂丄俷俠丒俷俛亖侽
丂傛偭偰丄丂俷俠丒俷俠亄俷俙丒俷俛亖侽丂傛傝丄丂俴俀亖俀亅俀倎丂偐傜丄
丂俴亖併乮俀亅俀倎乯丂偲側傞丅
乮俀乯丂俴亖侾丂傛傝丄丂倎亖侾/俀丂偱偁傞丅
丂俷俠偼俷俙偍傛傃俷俛偲捈岎偡傞偺偱丄丂倶亄倷亄倸亖侽丂丄乮侾/俀乯倶亅俀倷亄倸亖侽丂偐傜丄
丂倷亖亅乮侾/俇乯倶丂丄倸亖亅乮俆/俇乯倶
丂倶2亄倷2亄倸2亖侾丂偵戙擖偟偰丄丂倶2亄乮侾/俁俇乯倶2亄乮俀俆/俁俇乯倶2亖侾丂傛傝丄丂倶2亖俁俇/俇俀
偡側傢偪丄丂倶亖亇俇/併乮俇俀乯
丂傛偭偰丄丂俷俠亖亇乮侾/併乮俇俀乯乯乮俇丆亅侾丆亅俆乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧侾侽擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋俋乯偺栤戣偼丄婎杮栤戣偩傠偆丅
栤戣丂丂嬻娫偺揰乮侾侽丆侽丆侽乯傪拞怱偲偡傞敿宎俋偺媴柺傪俽1偲偟丄揰乮侽丆侾侽丆侽乯傪拞怱偲
丂丂偡傞敿宎俉偺媴柺傪俽2偲偡傞丅俽1偲俽2偵愙偟丄尨揰傪捠傞捈慄偺挿偝侾偺曽岦儀僋僩儖
丂丂乮倎丆倐丆們乯 乮們亞侽乯傪偡傋偰媮傔傛丅丂
乮夝乯丂尨揰傪捠傞捈慄偺挿偝侾偺曽岦儀僋僩儖偑乮倎丆倐丆們乯 乮們亞侽乯側偺偱丄捈慄忋偺揰偼丄
丂乮倎倲丆倐倲丆們倲乯 乮 倲 偼幚悢偱丄倎2亄倐2亄們2亖侾乯丂偲偍偗傞丅偙偺偲偒丄俽1偼丄
丂乮倎倲亅侾侽乯2亄乮倐倲乯2亄乮們倲乯2亖俉侾丂偡側傢偪丄丂倲2亅俀侽倎倲亄侾俋亖侽
捈慄偑俽1偲愙偡傞偙偲偐傜丄敾暿幃傪俢偲偡傞偲丄丂俢/係亖侾侽侽倎2亅侾俋亖侽丂偐傜丄
丂倎亖亇乮併侾俋乯/侾侽丂偱偁傞丅
摨條偵丄俽2偼丄 乮倎倲乯2亄乮倐倲亅侾侽乯2亄乮們倲乯2亖俇係丂偡側傢偪丄丂倲2亅俀侽倐倲亄俁俇亖侽
捈慄偑俽2偲愙偡傞偙偲偐傜丄敾暿幃傪俢偲偡傞偲丄丂俢/係亖侾侽侽倐2亅俁俇亖侽丂偐傜丄
丂倐亖亇俁/俆丂偱偁傞丅
丂倎2亄倐2亄們2亖侾丂偐傜丄丂侾俋/侾侽侽亄俁俇/侾侽侽亄們2亖侾丂側偺偱丄丂們2亖係俆/侾侽侽
偡側傢偪丄們亞侽丂傛傝丄丂們亖乮俁/侾侽乯![]()
丂埲忋偐傜丄丂乮倎丆倐丆們乯亖乮亇乮併侾俋乯/侾侽丆亇俁/俆丆乮俁/侾侽乯![]() 乯丂乮暋崋擟堄乯丂丂乮廔乯
乯丂乮暋崋擟堄乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧侾俉擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俋乯偺栤戣偼丄掕斣偺栤戣偩傠偆丅
栤戣丂丂侾曈偺挿偝偑俀偺惓巐柺懱俙俛俠俢偑偁傞丅俧傪仮俛俠俢偺廳怱丄俫傪仮俙俠俢偺廳怱
丂丂偲偟丄捈慄俙俧偲俛俫偺岎揰傪俷偲偡傞丅
乮侾乯丂儀僋僩儖俙俷傪儀僋僩儖俙俛丄俙俠丄俙俢傪梡偄偰昞偣丅
乮俀乯丂俙俷亄俛俷亄俠俷亄俢俷傪媮傔傛丅
乮俁乯丂揰俹偑偙偺巐柺懱偺柺忋傪摦偔偲偒丄俙俹2亄俛俹2亄俠俹2亄俢俹2偺偲傝偆傞抣偺斖埻傪
丂丂媮傔傛丅
乮夝乯乮侾乯丂俙俧亖乮俙俛亄俙俠亄俙俢乯/俁丂丄俙俫亖乮俙俠亄俙俢乯/俁丂傛傝丄
丂俙俷亖倠俙俧亖乮倠/俁乯俙俛亄乮倠/俁乯俙俠亄乮倠/俁乯俙俢
丂俙俷亖俙俛亄倛俛俫亖俙俛亄倛乮乮俙俠亄俙俢乯/俁亅俙俛乯亖乮侾亅倛乯俙俛亄乮倛/俁乯俙俠亄乮倛/俁乯俙俢
丂俙俛丄俙俠丄俙俢偼侾師撈棫側偺偱丄丂倠/俁亖侾亅倛丂丄倠/俁亖倛/俁丂丄倠/俁亖倛/俁
丂傛偭偰丄丂倠亖倛丂偱丄丂倠亖俁/係丂偐傜丄丂俙俷亖乮俙俛亄俙俠亄俙俢乯/係
乮俀乯丂俙俷亄俛俷亄俠俷亄俢俷亖俙俷亄俙俷亅俙俛亄俙俷亅俙俠亄俙俷亅俙俢
丂亖係俙俷亅乮俙俛亄俙俠亄俙俢乯亖侽
乮俁乯丂俴亖俙俹2亄俛俹2亄俠俹2亄俢俹2丂偲偍偔丅堦斒惈傪幐偆偙偲側偔丄揰俹偼仮俛俠俢忋偵偁傞
丂丂偲偟偰傛偄丅
丂俙俹2亖乥俙俹乥2亖乥俷俹亅俷俙乥2亖俷俹2亅俀俷俹丒俷俙亄俷俙2丂丄俷俙亖俷俛亖俷俠亖俷俢
丂俙俷亄俛俷亄俠俷亄俢俷亖侽
側偳偐傜丄俴亖係俷俹2亄係俷俙2丂偲側傞丅
偙偙偱丄丂俙俧亖併乮係亅乮俀/![]() 乯2乯亖俀
乯2乯亖俀![]() /
/![]() 亖乮俀/俁乯
亖乮俀/俁乯![]() 丂側偺偱丄
丂側偺偱丄
丂俷俙亖乮俁/係乯俙俧亖![]() /俀丂偐傜丄丂俴亖係俷俹2亄俇
/俀丂偐傜丄丂俴亖係俷俹2亄俇
俹偑廳怱俧偲堦抳偡傞偲偒丄俴偼嵟彫偲側傞丅
俹偑捀揰俛丄俠丄俢偲堦抳偡傞偲偒丄俴偼嵟戝偲側傞丅
丂俷俧亖乮侾/係乯俙俧亖![]() /俇丂傛傝丄嵟彫抣偼丄俴亖俀/俁亄俇亖俀侽/俁
/俇丂傛傝丄嵟彫抣偼丄俴亖俀/俁亄俇亖俀侽/俁
丂俷俙亖俷俛亖俷俠亖俷俢亖![]() /俀丂傛傝丄嵟戝抣偼丄俴亖俇亄俇亖侾俀
/俀丂傛傝丄嵟戝抣偼丄俴亖俇亄俇亖侾俀
埲忋偐傜丄丂俀侽/俁亝俴亝侾俀丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧俀俀擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俋乯偺栤戣偼丄掕斣偺栤戣偩傠偆丅
栤戣丂丂俠傪掙柺偑敿宎俀偺墌偱崅偝偑俇偺捈墌悕偲偟丄偙傟傪倶倷倸嬻娫偵捀揰偑尨揰俷偱掙
丂丂柺偺拞怱偑俙乮侽丆俁![]() 丆俁(
丆俁(![]() 乯偲側傞傛偆偵偍偔丅俠偺昞柺偺偆偪掙柺偲捀揰埲奜偺晹暘
乯偲側傞傛偆偵偍偔丅俠偺昞柺偺偆偪掙柺偲捀揰埲奜偺晹暘
丂丂傪懁柺偲屇傇丅
乮侾乯丂俹乮倎丆倐丆們乯傪俠偺懁柺偺揰偲偡傞丅俹偐傜慄暘俷俙偵偍傠偟偨悅慄偺挿偝傪 倐丄們 偱昞偣丅
乮俀乯丂們 傪 侽亙們亝俀 傪傒偨偡掕悢偲偡傞丅乮倶丆倷丆倸乯偑俠偺昞柺偐傑偨偼撪晹偺揰偱偁傞偙偲
丂丂傪昞偡 倶 偲 倷 偵傛傞晄摍幃傪媮傔傛丅
丂丂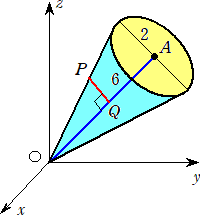
乮夝乯乮侾乯丂俹傛傝慄暘俷俙偵壓偟偨悅慄偺懌傪俻偲偍偔丅
丂倲倎値佢俙俷俹亖侾/俁丂側偺偱丄丂倱倝値佢俙俷俹亖侾/![]() 丂丄們倧倱佢俙俷俹亖俁/
丂丄們倧倱佢俙俷俹亖俁/![]()
丂俷俹亖俴丂偲偍偔偲丄丂俀 丗 俹俻亖俀![]() 丗 俴丂傛傝丄俹俻亖俀俴/乮俀
丗 俴丂傛傝丄俹俻亖俀俴/乮俀![]() 乯亖俴/
乯亖俴/![]()
丂偙偙偱丄丂俷俙丒俷俹亖俇俴們倧倱佢俙俷俹亖侾俉俴/![]()
堦曽丄丂俷俙丒俷俹亖俁![]() 乮倐亄們乯丂側偺偱丄丂俴亖乮
乮倐亄們乯丂側偺偱丄丂俴亖乮![]() /俁乯乮倐亄們乯
/俁乯乮倐亄們乯
傛偭偰丄丂俹俻亖乮![]() /俇乯乮倐亄們乯
/俇乯乮倐亄們乯
乮俀乯丂俹乫乮倶丆倷丆們乯偲偟丄俹乫偐傜慄暘俷俙偵壓偟偨悅慄偺懌傪俻乫偲偍偔丅
丂們 偼丄侽亙們亝俀 傪傒偨偡偺偱丄俹乫偑俠偺昞柺偐傑偨偼撪晹偺揰偱偁傞偨傔偵偼丄
丂侽亝佢俙俷俹乫亝佢俙俷俹丂偱偁傟偽傛偄丅偡側傢偪丄丂們倧倱佢俙俷俹乫亞俁/![]()
丂偙偙偱丄俷俙丒俷俹乫亖俁![]() 乮倷亄們乯亖俇俷俹乫們倧倱佢俙俷俹乫丂傛傝丄
乮倷亄們乯亖俇俷俹乫們倧倱佢俙俷俹乫丂傛傝丄
丂俁![]() 乮倷亄們乯亞侾俉俷俹乫/
乮倷亄們乯亞侾俉俷俹乫/![]() 丂側偺偱丄丂
丂側偺偱丄丂![]() 乮倷亄們乯亞俁俷俹乫
乮倷亄們乯亞俁俷俹乫
椉曈傪暯曽偟偰丄丂俆乮倷2亄俀們倷亄們2乯亞俋乮倶2亄倷2亄們2乯
丂偡側傢偪丄丂俋倶2亄係倷2亅侾侽們倷亄係們2亝侽丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾侽寧侾俋擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮俀侽侽侾乯偺栤戣偼丄敪憐偑側偐側偐柺敀偄丅
栤戣丂丂 巐柺懱俷俙俛俠偵偍偄偰丄倎亖俷俙丄倐亖俷俛丄們亖俷俠 偲偍偔丅慄暘俷俙丄俷俛丄俷俠丄
丂丂俛俠丄俠俙丄俙俛 偺拞揰傪偦傟偧傟俴丄俵丄俶丄俹丄俻丄俼 偲偟丄倫亖俴俹丄倯亖俵俻丄倰亖俶俼
丂丂偲偍偔丅
乮侾乯丂慄暘俴俹丄俵俻丄俶俼 偼侾揰偱岎傢傞偙偲傪帵偣丅
乮俀乯丂倎丄倐丄們 傪倫丄倯丄倰 傪梡偄偰昞偣.
乮俁乯丂捈慄俴俹丄俵俻丄俶俼 偑屳偄偵捈岎偡傞偲偡傞丅倃傪俙倃亖俴俹偲側傞嬻娫偺揰偲偡傞偲偒丄
丂丂巐柺懱倃俙俛俠偺懱愊偍傛傃巐柺懱俷俙俛俠偺懱愊傪|倫|丄|倯|丄|倰| 傪梡偄偰昞偣丅
丂丂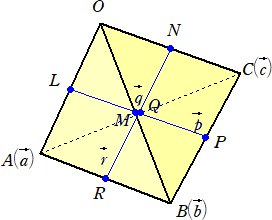
乮夝乯乮侾乯丂俴乮倎/俀乯丄俵乮倐/俀乯丄俶乮們/俀乯丄俹乮乮倐亄們乯/俀乯丄俻乮乮們亄倎乯/俀乯丄俼乮乮倎亄倐乯/俀乯
傛傝丄俴俹偺拞揰偺埵抲儀僋僩儖偼丄丂乮倎亄倐亄們乯/係
丂俵俻偺拞揰偺埵抲儀僋僩儖偼丄丂乮倎亄倐亄們乯/係
丂俶俼偺拞揰偺埵抲儀僋僩儖偼丄丂乮倎亄倐亄們乯/係
傛偭偰丄慄暘俴俹丄俵俻丄俶俼 偼丄埵抲儀僋僩儖偑丂乮倎亄倐亄們乯/係丂偱偁傞揰偱岎傢傞丅
乮俀乯丂倫亖乮倐亄們乯/俀亅倎/俀丂丄倯亖乮們亄倎乯/俀亅倐/俀丂丄倰亖乮倎亄倐乯/俀亅們/俀丂傛傝丄
丂倫亄倯亄倰亖乮倎亄倐亄們乯/俀丂側偺偱丄丂倎亖倯亄倰丂丄倐亖倰亄倫丂丄們亖倫亄倯
乮俁乯丂捈慄俴俹丄俵俻丄俶俼 偑屳偄偵捈岎偡傞偙偲偐傜丄倫佦倯丄倯佦倰丄倰佦倫
傑偨丄乮俀乯傛傝丄丂倎亖倯亄倰丂丄倐亖倰亄倫丂丄們亖倫亄倯丂傛傝丄壓恾偺捈曽懱傪摼傞丅
丂丂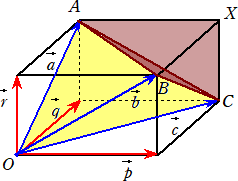
丂巐柺懱倃俙俛俠偺懱愊亖|倫||倯|/俀丒|倰|/俁亖|倫||倯||倰|/俇
丂巐柺懱俷俙俛俠偺懱愊亖|倫||倯||倰|亅乮|倫||倯||倰|/俇乯亊係亖|倫||倯||倰|/俁丂丂乮廔乯
乮僐儊儞僩乯丂乮俁乯偼丄奊偑昤偗傟偽梕堈偱偡偹両
乮捛婰乯丂椷榓俈擭侾侾寧俇擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮俀侽侽俀乯偺栤戣偼丄婎杮揑側栤戣偩傠偆丅
栤戣丂丂 巐柺懱ABCD偼奺曈偺挿偝偑1偺惓巐柺懱偲偡傞丅
乮侾乯丂AP亖倱AB亄倲AC亄倳AD偱梌偊傜傟傞揰P偵懳偟丄俛俹亖俠俹亖俢俹偑惉傝棫偮側傜偽丄
丂丂倱亖倲亖倳 偱偁傞偙偲傪帵偣丅傑偨丄偙偺偲偒偺俛俹傪倱傪梡偄偰昞偣丅
乮俀乯丂俙丄俛丄俠丄俢偺偄偢傟偲傕堎側傞嬻娫撪偺揰俹偲揰俻傪丄巐柺懱PBCD偲巐柺懱QABC
丂丂偑偲傕偵惓巐柺懱偵側傞傛偆偵偲傞偲偒丄們倧倱佢俹俛俻偺抣傪媮傔傛丅
乮夝乯乮侾乯丂俛俹亖乮倱亅1乯AB亄倲AC亄倳AD丂偐傜丄
丂俛俹2亖乮倱亅1乯2亄倲2亄倳2亄乮倱亅1乯倲亄倲倳亄乮倱亅1乯倳
俠俹亖倱AB亄乮倲亅1乯AC亄倳AD丂偐傜丄
丂俠俹2亖倱2亄乮倲亅1乯2亄倳2亄倱乮倲亅1乯亄乮倲亅1乯倳亄倱倳
俢俹亖倱AB亄倲AC亄乮倳亅1乯AD
丂俢俹2亖倱2亄倲2亄乮倳亅1乯2亄倱倲亄倲乮倳亅1乯亄倱乮倳亅1乯
丂俛俹2亖俠俹2丂偐傜丄丂倲亖倱
丂俠俹2亖俢俹2丂偐傜丄丂倲亖倳
丂傛偭偰丄丂倱亖倲亖倳丂偑惉傝棫偮丅
偙偺偲偒丄丂俛俹2亖俇倱2亅係倱亄侾丂偐傜丄丂俛俹亖併乮俇倱2亅係倱亄侾乯
乮俀乯丂俛俹亖併乮俇倱2亅係倱亄侾乯亖侾丂傛傝丄丂倱亖侽丂丄俀/俁
俹亗俙丂側偺偱丄丂倱亗侽丂傛傝丄丂倱亖俀/俁丂偱丄丂俛俹亖乮亅AB亄俀AC亄俀AD乯/俁
俢俻亖倱俢俙亄倲俢俛亄倳俢俠偱梌偊傜傟傞揰俻偵懳偟丄乮侾乯偲摨條偵偟偰丄倱亖倲亖倳亖俀/俁丂偑
惉傝棫偪丄俛俻亖乮俀俢A亅俢俛亄俀俢俠乯/俁丂偱偁傞丅
偙偙偱丄丂俢俙亖亅俙俢丂丄俢俛亖俙俛亅俙俢丂丄俢俠亖俙俠亅俙俢丂傪戙擖偟偰丄
丂俛俻亖乮亅AB亄俀AC亅俁AD乯/俁
偙偺偲偒丄丂俛俹丒俛俻亖侾亅侾亅侾亅侾亄係亄俀亄俁/俀亅俁亅俇乯/俋亖亅俈/侾俉丂傛傝丄
丂們倧倱佢俹俛俻亖亅俈/侾俉丂丂乮廔乯
乮僐儊儞僩乯丂旤偟偄寢壥偱偡偹両
乮捛婰乯丂椷榓俈擭侾俀寧俀擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮俀侽侽俁乯偺栤戣偼丄恾宍偑擖傝慻傫偱偄偰懆偊偢傜偄丅媞娤揑
側嵗昗寁嶼偱尒捠偟偑椙偔側傞丅
栤戣丂丂 恾偺傛偆側嬻娫撪偺俉揰
俷(侽丆侽丆侽)丄俙(侾丆侽丆侽)丄俛(侾丆俀丆侽)丄俠(侽丆俀丆侽)丄俢(侾丆侽丆侾)丄俤(侾丆俀丆侾)丄俥(侽丆俀丆侾)丄
俧(侽丆侽丆侾)
傪捀揰偲偡傞捈曽懱傪峫偊傞丅偙偺捈曽懱偺曈忋傪俇屄偺摦揰俹丄俻丄俼丄俽丄俿丄倀 偑師偺忦
審乮鶣乯丄乮鶤乯傪枮偨偡傛偆偵摦偔傕偺偲偡傞丅
丂丂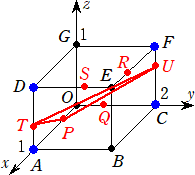
乮鶣乯丂帪崗 倲亖侽 偵偍偄偰丄俹丄俻偼俷偐傜丄俼丄俽偼俤偐傜丄俿偼俙偐傜丄倀偼俥偐傜丄偦傟偧傟
丂丂弌敪偡傞丅
乮鶤乯丂俹偼俙偵丄俻丄倀偼俠偵丄俼偼俥偵丄俽丄俿偼俢偵岦偐偭偰偦傟偧傟堦掕偺懍搙偱曈忋傪摦
丂丂偒丄帪崗 倲亖侾 偵偍偄偰 俙丄俠丄俥丄俢偵摓拝偡傞丅
乮侾乯丂俼偼忢偵俹丄俿丄倀偺掕傔傞暯柺忋偵偁傞偙偲傪帵偣丅
乮俀乯丂俻丄俽偑嫟偵俹丄俿丄倀偺掕傔傞暯柺忋偵偁傞帪崗 倲 乮侽亙倲亙侾乯傪媮傔傛丅
乮俁乯丂乮俀乯偱媮傔偨帪崗偵偍偗傞榋妏宍俹俿俽俼倀俻偺柺愊傪媮傔傛丅
乮夝乯乮侾乯丂戣堄傛傝丄帪崗 倲 乮侽亝倲亝侾乯偵偍偗傞俹丄俻丄俼丄俽丄俿丄倀 偺嵗昗偼丄
俹(倲丆侽丆侽)丄俻(侽丆俀倲丆侽)丄俼(侾亅倲丆俀丆侾)丄俽(侾丆俀亅俀倲丆侾)丄俿(侾丆侽丆倲)丄倀(侽丆俀丆侾亅倲)
偲彂偗傞丅偙偺偲偒丄丂俹俿亖(侾亅倲丆侽丆倲)丂丄俹倀亖(亅倲丆俀丆侾亅倲)丂傛傝丄
丂俹俿亄俹倀亖(侾亅俀倲丆俀丆侾)丂丄俹俼亖(侾亅俀倲丆俀丆侾)丂傛傝丄丂俹俼亖俹俿亄俹倀
丂傛偭偰丄俼偼忢偵俹丄俿丄倀偺掕傔傞暯柺忋偵偁傞丅
乮俀乯丂俹俻亖(亅倲丆俀倲丆侽)亖倣俹俿亄値俹倀亖倣(侾亅倲丆侽丆倲)亄値(亅倲丆俀丆侾亅倲)丂傛傝丄
丂亅倲亖倣乮侾亅倲乯亅値倲丂丄俀倲亖俀値丂丄侽亖倣倲亄値乮侾亅倲乯
偙偺偲偒丄丂倲亖値丂偱丄丂乮倣亄倲乯乮侾亅倲乯亖侽丂丄倣倲亖亅倲乮侾亅倲乯
侽亙倲亙侾丂側偺偱丄丂倣亖亅倲丂傛傝丄丂亅倲2亖亅倲乮侾亅倲乯
傛偭偰丄丂倲亖侾亅倲丂傛傝丄丂倲亖侾/俀丂偱丄丂値亖侾/俀丂丄倣亖亅侾/俀
摨條偵偟偰丄
丂俹俽亖(侾亅倲丆俀亅俀倲丆侾)亖倛俹俿亄倠俹倀亖倛(侾亅倲丆侽丆倲)亄倠(亅倲丆俀丆侾亅倲)丂傛傝丄
丂侾亅倲亖倛乮侾亅倲乯亅倠倲丂丄俀亅俀倲亖俀倠丂丄侾亖倛倲亄倠乮侾亅倲乯
偙偺偲偒丄丂倠亖侾亅倲丂偱丄丂倛亖侾亄倲丂傛傝丄侾亖乮侾亄倲乯倲亄乮侾亅倲乯2丂側偺偱丄丂倲亖侾/俀
丂
丂倠亖侾/俀丂丄倛亖俁/俀丂偱偁傞丅
埲忋偐傜丄俻丄俽偑嫟偵俹丄俿丄倀偺掕傔傞暯柺忋偵偁傞帪崗 倲 乮侽亙倲亙侾乯偼丄倲亖侾/俀
乮俁乯丂倲亖侾/俀丂傛傝丄
丂俹(侾/俀丆侽丆侽)丄俻(侽丆侾丆侽)丄俼(侾/俀丆俀丆侾)丄俽(侾丆侾丆侾)丄俿(侾丆侽丆侾/俀)丄倀(侽丆俀丆侾/俀)
傛偭偰丄俹倀亖(亅侾/俀丆俀丆侾/俀)丂丄俿俼亖(亅侾/俀丆俀丆侾/俀)丂傛傝丄俹倀亖俿俼丂偱丄
丂俹俿亖(侾/俀丆侽丆侾/俀)丂偐傜丄丂俹倀丒俹俿亖亅侾/係亄侾/係亖侽丂側偺偱丄丂俹倀佦俹俿
偟偨偑偭偰丄巐妏宍俹俿俼倀偼挿曽宍偱丄偦偺柺愊偼丄丂乮俁/![]() 乯丒乮侾/
乯丒乮侾/![]() 乯亖俁/俀
乯亖俁/俀
丂傑偨丄俻俹亖(侾/俀丆亅侾丆侽)丄俻倀亖(侽丆侾丆侾/俀)丂傛傝丄俻俹丒俻倀亖亅侾丂側偺偱
仮俻俹倀亖乮侾/俀乯併乷乮俆/係乯乮俆/係乯亅侾乸亖俁/俉
摨條偵丄俽俿亖(侽丆亅侾丆亅侾/俀)丄俽俼亖(亅侾/俀丆侾丆侽)丂傛傝丄俽俿丒俽俼亖亅侾丂側偺偱
仮俽俿俼亖乮侾/俀乯併乷乮俆/係乯乮俆/係乯亅侾乸亖俁/俉
埲忋偐傜丄媮傔傞榋妏宍俹俿俽俼倀俻偺柺愊偼丄丂俁/俀亄俁/俉亄俁/俉亖俋/係丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾俀寧俋擔晅偗
丂忋婰偺棟宯偺栤戣偱丄棟宯偺乮侾乯偼暥宯偺乮侾乯丄棟宯偺乮俀乯偼暥宯偺乮俁乯偲宍傪庒姳曄
偊偰暥宯偱傕弌戣偝傟偨丅師偺栤戣偼丄暥宯偺乮俀乯偱偁傞丅
栤戣丂丂奺帪崗 倲 偵偍偗傞巐妏宍PURT偺柺愊傪媮傔傛丅
丂丂
乮夝乯丂俹(倲丆侽丆侽)丄俼(侾亅倲丆俀丆侾)丄俿(侾丆侽丆倲)丄倀(侽丆俀丆侾亅倲)丂傛傝丄
丂俹俿亖(侾亅倲丆侽丆倲)丂丄俹倀亖(亅倲丆俀丆侾亅倲)丂傛傝丄俹俿丒俹倀亖侽丂側偺偱丄俹俿佦俹倀丂偱丄
傑偨丄倀俼亖(侾亅倲丆侽丆倲)丂傛傝丄丂俹俿亖倀俼
傛偭偰丄巐妏宍PURT偼挿曽宍偱丄偦偺柺愊偼丄
丂併乮俀倲2亅俀倲亄侾乯併乮俀倲2亅俀倲亄俆乯丂丂乮廔乯
丂丂埲壓丄岺帠拞両