ペル方程式 
次の形の不定方程式は、数学のいろいろなところで現れる。
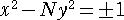
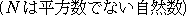
この方程式は、ペル方程式 といわれる。
もっとも、ペル自身は、この方程式とは無関係らしいが、オイラーによって誤解された後、
そう呼ばれ続けているそうだ。
フェルマー(1601〜1665)が出した次の問題(1657年):
X2−61Y2=1 の自然数解を求めよ。
が、そもそもの発端である。 ( (1766319049,226153980) が解になる!)
ペル方程式が必ず解を持つことは、ラグランジュ(1766年頃)により示されている。また、
解を能率よく計算する方法も、ブラウンカー、ウォリス(1657年)、オイラー(1753年)に
より、既に見出されている。(具体例はこちらを参照)
ペル方程式に関連して、基本事項を整理しておこう。
(1)  は無理数である。
は無理数である。
(2) 集合 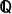 (
( )={ x+y
)={ x+y | x∈
| x∈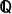 、y∈
、y∈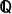 、
、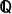 は有理数全体の集合}
は有理数全体の集合}
は、四則演算(+、−、×、÷)について閉じている。
(詳しくは、実2次体となる。)
(3) α = x+y の共役を、α’ = x−y
の共役を、α’ = x−y とするとき、
とするとき、
( x , y ) が、ペル方程式の解 ⇔ α・α’=±1
(4) ( x1 , y1 )、 ( x2 , y2 ) を、ペル方程式の自明でない自然数解とする。
このとき、次の関係が成り立つ。
x1 < x2 ⇔ y1 < y2 ⇔ x1+y1 < x2+y2
< x2+y2
実際に、x12− Ny12 = x22− Ny22 のとき、x12− x22 = N(y12− y22)
よって、 x1 < x2 ⇔ y1 < y2 ⇔ x1+y1 < x2+y2
< x2+y2 は明らか。
は明らか。
次に、x12− Ny12 =−1、 x22− Ny22 =1 のときを考える。
x1 < x2 とする。このとき、
Ny12 = x12+1=(x1+1)2−2x1<(x1+1)2−1≦ x22−1= Ny22
よって、 y1 < y2 となる。逆に、 y1 < y2 とする。このとき、
x12= Ny12 −1<Ny12 +1<N(y1+1)2 +1≦Ny22 +1=x22
よって、 x1 < x2 となる。
したがって、 x1 < x2 ⇔ y1 < y2 ⇔ x1+y1 < x2+y2
< x2+y2
同様にして、x12− Ny12 =1、 x22− Ny22 =−1 のときも成り立つことが分
かる。
このことから、ペル方程式の最小の解を求めるには、x (または y ) が最小の解を求め
ればよい。
(5) ( x , y ) を、ペル方程式の自明でない解とする。 α = x+y に対して、
に対して、
αn = xn+yn で定まる ( xn , yn ) もペル方程式の解となる。
で定まる ( xn , yn ) もペル方程式の解となる。
実際に、xn2− Nyn2=αn・(α’)n=(α・α’)n=(±1)n=±1 より、明らか。
ペル方程式において、( ±1 , 0 ) は自明な解といわれる。 (5)から、ペル方程式は、
1つでも自明でない解があれば、無限に解がある。
さらに、次も成り立ち、ペル方程式の解の構造が明らかとなる。
(6) ペル方程式
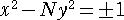
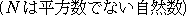
の解 ( X , Y ) (ただし、X + Y >0 で、X、Yは整数)の集合を P とおく。
>0 で、X、Yは整数)の集合を P とおく。
( a ,b )∈ P を、α = a + b >1 を満たす P の要素のうちで、最小な
>1 を満たす P の要素のうちで、最小な
ものとする。(格子点の理論を用いて、その存在は保証される。)
このとき、ペル方程式の全ての解は、αn (n は整数)により与えられる。
いま、整数 n に対して、αn = xn+yn で定まる ( xn , yn )の集合を Q とおく。
で定まる ( xn , yn )の集合を Q とおく。
(5)より、 Q ⊂ P であるので、 P ⊂ Q であることを示せば十分である。
任意の ( X , Y )∈ P をとる。まず、 X+Y >1 の場合について考える。
>1 の場合について考える。
このとき、適当な自然数 n が存在して、
( a + b )n≦ X + Y
)n≦ X + Y < ( a + b
< ( a + b )n+1
)n+1
が成り立つ。 よって、
1 ≦ ( X + Y )( a + b
)( a + b )−n < a + b
)−n < a + b
ところで、( x , y )、( u , v )∈ P に対して、
( x + y )( u + v
)( u + v )m = w + z
)m = w + z ( m は、任意の整数)
( m は、任意の整数)
とおくと、 ( w , z )∈ P であることが、数学的帰納法により示すことができる。
このことから、
( X + Y )( a + b
)( a + b )−n =c + d
)−n =c + d
となる ( c , d )は P の要素である。しかるに、a + b が最小の解であることか
が最小の解であることか
ら、 c + d = 1 でなければならない。
= 1 でなければならない。
よって、このとき、 X + Y = ( a + b
= ( a + b )n = αn となり、( X , Y )∈ Q
)n = αn となり、( X , Y )∈ Q
すなわち、 P ⊂ Q である。
次に、 X+Y <1 の場合について考える。 このとき、(X+Y
<1 の場合について考える。 このとき、(X+Y )-1 >1 なの
)-1 >1 なの
で、上記の結果より、(X+Y )-1= αn と書ける。 よって、この場合も、
)-1= αn と書ける。 よって、この場合も、
X+Y = α−n となり、 ( X , Y )∈ Q すなわち、 P ⊂ Q である。
= α−n となり、 ( X , Y )∈ Q すなわち、 P ⊂ Q である。
以上から、 P = Q であることが示された。
(参考文献:ホームページ「青空学園数学科」 の中の 『ペル方程式の解の構造』 )
ペル方程式の応用例 (こんなにいろいろ応用例があるとは、正直驚きである!)
◎ 平方根2を求める数列 ・・・ ペル方程式 X2−2Y2=1 の解の比 X/Y の考察
◎ 平方数となる和 ・・・・・・・・・ 自然数の和が平方数となる場合の項数とペル方程
式の解との関係
◎ ある2項係数の関係 ・・・・・ 判別式が平方数になるとき、ペル方程式との接点が
生まれる
(参考文献:和田秀男 著 数の世界 整数論への道 (岩波書店)
北村泰一 著 数論入門 (槙書店))
(追記) ペル方程式において、Nの値が一桁の自然数ならば、最小の解を見出すことは、
比較的易しい。しかし、Nの値がある程度大きくなると、最小の解を見出すために
いくつかの値を代入して検算する方法では、甚だ困難であるといわねばならない。
この問題に対して、最小の解は必ず存在すること(ラグランジュ)、最小の解を求めるアル
ゴリズム(オイラー等)については、先人たちによって既に解決済みである。
ここでは、具体例を通して、最小の解の求め方を整理しておきたい。
例 ペル方程式 X2−29Y2=±1 の最小の解を求めよ。
最小の解を求めるために、次の漸化式が用いられる。
an+1 = an-1+knan (n=0、1、2、・・・) ただし、a-1= 、a0=1
、a0=1
ここで、kn = [bn] (bn を超えない最大の整数)で、bn=−a’n-1/a’n
ただし、a = x+y に対して、a’は、a の共役で、a’= x−y
に対して、a’は、a の共役で、a’= x−y
このとき、
このような漸化式に対して、bn の分母が 1 になる n の値が必ず存在する(ラグランジュ)。
そのときの n に対して、an が最小の解を与える(オイラー)。
ということが知られている。
上の漸化式に従って、順次求めてもよいが、計算が煩雑になるので、通常次の式を用い
て、bn は計算される。
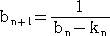 |
・・・・・・・・・・(*) |
実際に、
bn+1=−a’n/a’n+1 =−a’n/(a’n-1+kna’n)=1/(−(a’n-1/a’n)−kn)=1/(bn−kn)
より成り立つことが分かる。
それでは、計算を実行してみよう。
b0=−a’-1/a’0 =−(− )/1=
)/1= より、k0=[
より、k0=[ ]=5
]=5
よって、a1=a-1+k0a0= +5
+5
b1=1/( b0−k0)=1/( −5)=(5+
−5)=(5+ )/4 より、k1=[ b1]=2
)/4 より、k1=[ b1]=2
よって、a2=a0+k1a1=1+2( +5)=11+2
+5)=11+2
b2=1/( b1−k1)=4/( −3)=(3+
−3)=(3+ )/5 より、k2=[ b2]=1
)/5 より、k2=[ b2]=1
よって、a3=a1+k2a2= +5+(11+2
+5+(11+2 )=16+3
)=16+3
b3=1/( b2−k2)=5/( −2)=(2+
−2)=(2+ )/5 より、k3=[ b3]=1
)/5 より、k3=[ b3]=1
よって、a4=a2+k3a3=11+2 +(16+3
+(16+3 )=27+5
)=27+5
b4=1/( b3−k3)=5/( −3)=(3+
−3)=(3+ )/4 より、k4=[ b4]=2
)/4 より、k4=[ b4]=2
よって、a5=a3+k4a4=16+3 +2(27+5
+2(27+5 )=70+13
)=70+13
b5=1/( b4−k4)=4/( −5)=(5+
−5)=(5+ )/1
)/1
したがって、b5 の分母が1になったので、a5 が最小の解を与える。
実際に、702−29・132=4900−4901=−1 となっている。(念のため、確認!)
(このような解を発見するのは、コンピュータの得意分野だろう。しかし、手計算でも確実に
求められることに、数学本来の美しさを感じる。オイラー、ラグランジュに感謝したい!)
また、X2−29Y2=1 の最小の解を求めるには、
(70+13 )2=9801+1820
)2=9801+1820 より、(X,Y)=(9801,1820)
より、(X,Y)=(9801,1820)
実際に、98012−29・18202=96059601−29・3312400
=96059601−96059600=1
が成り立つ。
(追々記) 上記の計算は、多少整理されているとはいえ、まだまだ煩雑という感じは拭え
ない。
次のような、アルゴリズムが確立している。
オイラー(1765年)によれば、
ana’n-1=(−1)n-1( +gn) となる整数 gn が存在して、hn=| ana’n| とおくとき、 +gn) となる整数 gn が存在して、hn=| ana’n| とおくとき、 |
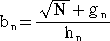 |
・・・・・・・・・・(**) |
が成り立つ。
| この性質に着目すれば、 |
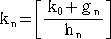 |
が成り立つ。 |
実際に、
kn = [bn] = [( +gn)/hn] =[([
+gn)/hn] =[([ ]+gn)/hn]=[(k0+gn)/hn] から明らか。
]+gn)/hn]=[(k0+gn)/hn] から明らか。
したがって、kn を効率的に求めるためには、gn、hn を効率的に求めればよいことになる。
ところで、(*)に(**)を代入すると、
bn+1=1/(bn−kn)=( −gn+knhn)/((N−(gn−knhn)2)/hn) なので、
−gn+knhn)/((N−(gn−knhn)2)/hn) なので、
gn+1=−gn+knhn 、 hn+1=(N−g2n+1)/hn
が成り立てばよい。このとき、
hn+1=(N−g2n+1)/hn=(N−g2n+2gnknhn−k2nh2n)/hn
=(N−g2n)/hn+kn(2gn−knhn)
=hn-1+kn(gn−gn+1)
となり、g0=0、h0=1 から、上記漸化式により、順次 gn、hn、kn が求められる。
このとき、ある n に対して、hn=1 となることが知られている(ラグランジュ 1766年頃)。
ところで、次の定理(Moir 1874年)によれば、hn は、hn=1 となるまで計算しなくてもよ
いことが分かる。(実は、hn は対称性を有している!)
定理(Moir 1874年)
n=1、2、・・・ に対して、初めて hn=1 になるものとする。
初めて gm=gm+1 または hm=hm+1 となるとき、n と m には、次の関係式が
成り立つ。 gm=gm+1 ⇔ n = 2m
hm=hm+1 ⇔ n = 2m+1
次に、an= xn+yn として、xn、yn の漸化式を求めてみよう。
として、xn、yn の漸化式を求めてみよう。
an+1 = an-1+knan に代入して、 an+1=xn-1+yn-1 +kn(xn+yn
+kn(xn+yn )
)
=xn-1+knxn+(yn-1+knyn)
よって、 xn+1=xn-1+knxn 、 yn+1=yn-1+knyn となる。
ところで、yn が分かると、実は、xn は、次式により、求められる。
xn=gnyn+hnyn-1
実際に、( +gn)/hn=bn=−a’n-1/a’n=−(xn-1−yn-1
+gn)/hn=bn=−a’n-1/a’n=−(xn-1−yn-1 )/(xn−yn
)/(xn−yn ) より
) より
分母を払って、 hn(−xn-1+yn-1 )=(
)=( +gn)(xn−yn
+gn)(xn−yn )
)
両辺の の係数を比較して、 hnyn-1=xn−gnyn より成り立つ。
の係数を比較して、 hnyn-1=xn−gnyn より成り立つ。
上記で、hn がそうであったように、an もすべて計算する必要がないことが知られている。
定理 n = 2m ならば、an=am2/hm
n = 2m+1 ならば、an=amam+1/hm
以上のアルゴリズムは、和田秀男 著 数の世界(岩波書店)を、参考にさせていただいた。
詳しい証明等は、上記書籍にあたられたい。
それでは、上記の例について、再度計算を実行してみよう。
| n |
0 |
1 |
2 |
3 |
| gn |
0 |
5 |
3 |
2 |
| hn |
1 |
4 |
5 |
5 |
| kn |
5 |
2 |
1 |
1 |
|
g0=0、h0=1 |
b0= より、k0=[b0]=5 より、k0=[b0]=5 |
| gn+1=−gn+knhn |
| hn+1=(N−g2n+1)/hn |
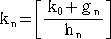 |
上記の計算から、h2=h3 が成り立つので、Moirの定理により、h5=1 となる。
このとき、定理より、 a5=a2a3/h2 =a2a3/5 となる。
条件より、a-1= 、a0=1 なので、y-1=1、y0=0 である。
、a0=1 なので、y-1=1、y0=0 である。
yn+1=yn-1+knyn 、xn=gnyn+hnyn-1 なので、次の表を埋めることができる。
| n |
0 |
1 |
2 |
3 |
| gn |
0 |
5 |
3 |
2 |
| hn |
1 |
4 |
5 |
5 |
| kn |
5 |
2 |
1 |
1 |
| yn |
0 |
1 |
2 |
3 |
| xn |
1 |
5 |
11 |
16 |
|
左の表により、 a2=11+2 、a3=16+3 、a3=16+3
よって、 a2a3=(11+2 )(16+3 )(16+3 ) )
=350+65
したがって、a5=70+13 |
(これらの計算は、先の計算結果と一致する。)
(コメント) あんなに煩雑だった計算が、ほぼ暗算で、全く機械的に表にまとめられること
に、感動しています!...!(^^)!
(追記) 平成24年3月4日付け
当HPの掲示板「出会いの泉」に、当HPがいつもお世話になっているHN「GAI」さんが「情
報を求む」ということで、ペル方程式の問題を書き込まれた。
x2−94y2=1 を満たす整数解の組(x,y)を5組ほど知りたいのですが・・・。
らすかるさんが解を5組求められた。(平成24年3月4日付け)
(x,y)=(1,0)、(2143295,221064)、(9187426914049,947610731760)、
(39382732335491159615,4062018686654877336)、
(168817626601983862467148801,17412208682026983028992480)
(コメント) らすかるさんは、多分プログラムを書いて求められたのだろう。
(掲示板に解を書き込もうとしたら、らすかるさんの方がより詳しい解を求められ先を越されてしまった。)
ここでは、手計算で示したいと思う。
漸化式 an+1 = an-1+knan (n=0、1、2、・・・) ただし、a-1=√94、a0=1
ここで、kn = [bn] (bn を超えない最大の整数)で、bn=−a’n-1/a’n
ただし、a = x+y√94 に対して、a’は、a の共役で、a’= x−y√94
を考えるとき、bn の分母が 1 になる n の値が必ず存在する(ラグランジュ)。そのときの
n に対して、an が最小の解を与える(オイラー)
ということが知られている。ただし、bn は次式で計算される。
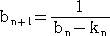
bn の分母が 1 になるまで結構手数が伸びたので結果だけ明記します。
b0=√94 なので、k0=9 このとき、 a1=9+√94
b1=(9+√94)/13 なので、k1=1 このとき、 a2=10+√94
b2=(4+√94)/6 なので、k2=2 このとき、 a3=29+3√94
b3=(8+√94)/5 なので、k3=3 このとき、 a4=97+10√94
b4=(7+√94)/9 なので、k4=1 このとき、 a5=126+13√94
b5=(2+√94)/10 なので、k5=1 このとき、 a6=223+23√94
b6=(8+√94)/3 なので、k6=5 このとき、 a7=1241+128√94
b7=(7+√94)/15 なので、k7=1 このとき、 a8=1464+151√94
b8=(8+√94)/2 なので、k8=8 このとき、 a9=12953+1336√94
b9=(8+√94)/15 なので、k9=1 このとき、 a10=14417+1487√94
b10=(7+√94)/3 なので、k10=5 このとき、 a11=85038+8771√94
b11=(8+√94)/10 なので、k11=1 このとき、 a12=99455+10258√94
b12=(2+√94)/9 なので、k12=1 このとき、 a13=184493+19029√94
b13=(7+√94)/5 なので、k13=3 このとき、 a14=652934+67345√94
b14=(8+√94)/6 なので、k14=2 このとき、 a15=1490361+153719√94
b15=(4+√94)/13 なので、k15=1 このとき、 a16=2143295+221064√94
b16=(9+√94)/1 なので、 a16=2143295+221064√94 が最小の解を与える。
らすかるさんの解を得るには、順次 a16n (n=2、3、4、5、6、・・・)を計算すればよい。
和田秀男 著 数の世界(岩波書店)にあるアルゴリズムに従って計算してみよう。
g0=0、h0=1 で、b0=√94 より、k0=[b0]=9
gn+1=−gn+knhn 、hn+1=(N−g2n+1)/hn 、
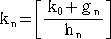 なる漸化式を用いて、順次計算し、表を埋めると、
なる漸化式を用いて、順次計算し、表を埋めると、
| n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| gn |
0 |
9 |
4 |
8 |
7 |
2 |
8 |
7 |
8 |
8 |
| hn |
1 |
13 |
6 |
5 |
9 |
10 |
3 |
15 |
2 |
15 |
| kn |
9 |
1 |
2 |
3 |
1 |
1 |
5 |
1 |
8 |
1 |
|
上記の計算から、g8=g9 が成り立つので、Moirの定理により、h16=1 となる。
このとき、定理より、 a16=a82/h8 =a82/2 となる。
条件より、a-1=√94、a0=1 なので、y-1=1、y0=0 である。
yn+1=yn-1+knyn 、xn=gnyn+hnyn-1 なので、次の表を埋めることができる。
| n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| gn |
0 |
9 |
4 |
8 |
7 |
2 |
8 |
7 |
8 |
| hn |
1 |
13 |
6 |
5 |
9 |
10 |
3 |
15 |
2 |
| kn |
9 |
1 |
2 |
3 |
1 |
1 |
5 |
1 |
8 |
| yn |
0 |
1 |
1 |
3 |
10 |
13 |
23 |
128 |
151 |
| xn |
1 |
9 |
10 |
29 |
97 |
126 |
223 |
1241 |
1464 |
|
上の表により、 a8=1464+151√94 なので、
よって、 a16=a82/h8 =(1464+151√94)2/2
=2143295+221064√94
これらの計算は、先の計算結果と一致する。
(コメント) 決まり切ったアルゴリズムとはいえ、随分昔にやった計算なので、思い出すのに
時間がかかりました...f(^^;)。
S(H)さんからのコメントです。(平成24年3月4日付け)
らすかる様の助言から多数なので、11組。
11111111111111111111111111111111111111111組も叶う。(→ 参考 、参考2)
S(H)さんが考察されました。(平成24年3月5日付け)
先ず、真ん中の問題を眺めて下さい。
たった2回 f・f では侘しく本質を失うので、大いに反復 fn (n∈N) しました。
(8x + 21)/(3x + 8) 、(127x + 336)/(48x + 127) 、(2024x + 5355)/(765x + 2024)
(32257x + 85344)/(12192x + 32257) 、(514088x + 1360149)/ (194307x
+ 514088)
(8193151x + 21677040)/(3096720x + 8193151)
(130576328x + 345472491)/(49353213x + 130576328)
(2081028097x + 5505882816)/(786554688x + 2081028097)
(33165873224x + 87748652565)/(12535521795x + 33165873224)
そして、これから続々産まれる
82 - 7・32 、1272 - 7・482 、20242 - 7・7652 、・・・ は、全て、不定方程式 _______=1 の
解です。高校生に教えて學費を稼ぎ親の負担を軽減するように飯高先生に促された學生が
高校生に質問された。
(0) 上の広大の問題のf(x)は、どのようにして誕生したのか?丁寧に教えてください。
(1) √7 のとき、あの f(x) なら、√94 のとき、丁寧に f(x) を導出して下さい。
(2) そして、下の各無理数について、f(x) を丁寧に導出して下さい。
{√7,√569,√1249,√2003,√2777,√3607,√4447,√5309,√6173,√7027,√7949,√8861,
√9767,√10691,√11699,√12589,√13553,√14549,√15443,√16427,√17419}
高校生に上問を質問された學生は、即答できず次回に説明するよとお暇した。そして、研
究室で此の問題について、喧々諤々していたら、飯高先生が入室され、瞬時に、その問題
の背景は____だっ!顔をされた。自分達で考えなさいと暗黙のうちにおっしゃたようなので、考
える価値が在ると自らに課す課題とした。
こんどは、真ん中以外も観て下さい。殆ど全て、背景を激白したと同じですが、(0)(1)(2)を
高校生や大學生に是非丁寧に解説して下さい。
空舟さんからのコメントです。(平成24年3月5日付け)
2次体の単数という見方もでき、Webサイト「2次体の単数と類数(その1)」がかなり詳し
く述べておられます。
ペル方程式は√mの連分数展開を用いると非常に簡単に求められるのですが,最小解
がmと較べて非常に大きい例としては、
m ε ノルム
46 24335+3588√46 +1
94 2143295+221064√94 +1
・・・
94は、大きい例の1つだったようですね。
GAI さんが、「x2−Dy2=1 の自然数解」について、探索されました。
(平成24年3月6日付け)
ほんの一週間前までは、数学計算ソフトには無縁であった私に、皆さんのおかげで、ペル
方程式の解をなんの苦も無く思う存分見つけ出す技を与えてくれました。その道に詳しい方
は下記の数字の羅列をなんとも思われないでしょうが、私にはうれしくてたまりません。こん
な力を誰にでも使えるように理論が整備されており、それを実行させるプログラムが開発さ
れており、疑問に思ったことに誠意を持って答えて頂く皆さんがおられて始めて私には自分
の意思で手にできる結果なのです。
ネットで知れば知るほど、いろいろな方がそれぞれ得意分野を持っておられ、日常では決
して得られない情報を提示して頂いていることに気付かされます。私も、なにか人に喜んで
もらえる情報を提供できるよう精進していきたいです。
D:
小さいほうから5組の解
2:{{3, 2}, {17, 12}, {99, 70}, {577, 408}, {3363, 2378}}
3:{{2, 1}, {7, 4}, {26, 15}, {97, 56}, {362, 209}}
5:{{9, 4}, {161, 72}, {2889, 1292}, {51841, 23184}, {930249, 416020}}
6:{{5, 2}, {49, 20}, {485, 198}, {4801, 1960}, {47525, 19402}}
7:{{8, 3}, {127, 48}, {2024, 765}, {32257, 12192}, {514088, 194307}}
8:{{3, 1}, {17, 6}, {99, 35}, {577, 204}, {3363, 1189}}
10:{{19, 6}, {721, 228}, {27379, 8658}, {1039681, 328776}, {39480499,
12484830}}
11:{{10, 3}, {199, 60}, {3970, 1197}, {79201, 23880}, {1580050, 476403}}
12:{{7, 2}, {97, 28}, {1351, 390}, {18817, 5432}, {262087, 75658}}
13:{{649, 180}, {842401, 233640}, {1093435849, 303264540}, {1419278889601, 393637139280},
{1842222905266249, 510940703520900}}
14:{{15, 4}, {449, 120}, {13455, 3596}, {403201, 107760}, {12082575, 3229204}}
15:{{4, 1}, {31, 8}, {244, 63}, {1921, 496}, {15124, 3905}}
17:{{33, 8}, {2177, 528}, {143649, 34840}, {9478657, 2298912}, {625447713,
151693352}}
18:{{17, 4}, {577, 136}, {19601, 4620}, {665857, 156944}, {22619537, 5331476}}
19:{{170, 39}, {57799, 13260}, {19651490, 4508361}, {6681448801, 1532829480}}
20:{{9, 2}, {161, 36}, {2889, 646}, {51841, 11592}, {930249, 208010}}
21:{{55, 12}, {6049, 1320}, {665335, 145188}, {73180801, 15969360}, {8049222775,
1756484412}}
22:{{197, 42}, {77617, 16548}, {30580901, 6519870}, {12048797377, 2568812232},
{4747195585637, 1012105499538}}
23:{{24, 5}, {1151, 240}, {55224, 11515}, {2649601, 552480}, {127125624,
26507525}}
24:{{5, 1}, {49, 10}, {485, 99}, {4801, 980}, {47525, 9701}}
26:{{51, 10}, {5201, 1020}, {530451, 104030}, {54100801, 10610040}, {5517751251,
1082120050}}
27:{{26, 5}, {1351, 260}, {70226, 13515}, {3650401, 702520}, {189750626,
36517525}}
28:{{127, 24}, {32257, 6096}, {8193151, 1548360}, {2081028097, 393277344},
{528572943487,
99890897016}}
29:{{9801, 1820}, {192119201, 35675640}, {3765920568201, 699313893460},
{73819574785756801,
13707950903927280}, {1447011301184484245001, 268703252919468649100}}
30:{{11, 2}, {241, 44}, {5291, 966}, {116161, 21208}, {2550251, 465610}}
31:{{1520, 273}, {4620799, 455910}, {10881980810, 1329864627}, {27795255169501,
3170260455180}, {69078702089829860, 8063643729550773}}
32:{{17, 3}, {577, 102}, {19601, 3465}, {665857, 117708}, {22619537, 3998607}}
33:{{23, 4}, {1057, 184}, {48599, 8460}, {2234497, 388976}, {102738263,
17884436}}
34:{{35, 6}, {2449, 420}, {171395, 29394}, {11995201, 2057160}, {839492675,
143971806}}
35:{{6, 1}, {71, 12}, {846, 143}, {10081, 1704}, {120126, 20305}}
37:{{73, 12}, {10657, 1752}, {1555849, 255780}, {227143297, 37342128},
{33161365513,
5451694908}}
38:{{37, 6}, {2737, 444}, {202501, 32850}, {14982337, 2430456}, {1108490437,
179820894}}
39:{{25, 4}, {1249, 200}, {62425, 9996}, {3120001, 499600}, {155937625,
24970004}}
40:{{19, 3}, {721, 114}, {27379, 4329}, {1039681, 164388}, {39480499,
6242415}}
41:{{2049, 320}, {8396801, 1311360}, {34410088449, 5373952960}, {141012534067201,
22022457918720}, {577869330197301249, 90248027176961600}}
42:{{13, 2}, {337, 52}, {8749, 1350}, {227137, 35048}, {5896813, 909898}}
43:{{3482, 531}, {24248647, 3697884}, {168867574226, 25752063645}, {1175993762661217,
179337367525896}, {8189620394305140962, 1248905401698276099}}
44:{{199, 30}, {79201, 11940}, {31521799, 4752090}, {12545596801, 1891319880},
{4993116004999, 752740560150}}
45:{{161, 24}, {51841, 7728}, {16692641, 2488392}, {5374978561, 801254496},
{1730726404001,
258001459320}}
46:{{24335, 3588}, {1184384449, 174627960}, {57643991108495, 8499142809612},
{2805533046066067201, 413653280369188080}, {136545293294391499564175,
20132505147069241043988}}
47:{{48, 7}, {4607, 672}, {442224, 64505}, {42448897, 6191808}, {4074651888,
594349063}}
48:{{7, 1}, {97, 14}, {1351, 195}, {18817, 2716}, {262087, 37829}}
50:{{99, 14}, {19601, 2772}, {3880899, 548842}, {768398401, 108667944}, {152139002499,
21515704070}}
S(H)さんからのコメントです。(平成24年3月7日付け)
「2章 Pell方程式と連分数展開 」において、
連分数展開 √94=9 [1, 2, 3, 1, 1, 5, 1, 8, 1, 5, 1, 1, 3, 2, 1, 18] から、Pell方程式の初期解
x=2143295 、y=221064
となるまでしか在りません....。
203586164707 のとき、√203586164707 の連分数展開を求め、Pell方程式の初期解を求
めてください。(→ 参考:「ルートの整数部分,小数部分」)
GAI さんが、ペル方程式から、少し拡張した「変形ペル方程式」について考察された。
(平成24年4月4日付け)
x2 - Dy2 = L を満たす自然数(x,y)の変化を調査してみました。
| L=1 |
|
L=2 |
|
L=3 |
|
L=4 |
|
L=5 |
x y D
3 2 2
17 12 2
7 4 3
26 15 3
9 4 5
5 2 6
49 20 6
8 3 7
17 6 8
99 35 8
19 6 10
10 3 11
7 2 12
97 28 12
15 4 14
31 8 15
33 8 17
17 4 18
9 2 20
55 12 21
24 5 23
49 10 24
51 10 26
26 5 27
11 2 30
17 3 32
23 4 33
|
|
x y D
35 6 34
71 12 35
73 12 37
37 6 38
25 4 39
19 3 40
13 2 42
48 7 47
97 14 48
99 14 50
50 7 51
89 12 55
15 2 56
31 4 60
63 8 62
65 8 66
33 4 68
17 2 72
26 3 75
53 6 78
80 9 79
82 9 83
55 6 84
28 3 87
19 2 90
39 4 95
49 5 96
99 10 98 |
|
x y D
10 7 2
58 41 2
45 17 7
39 7 31
59 7 71
88 7 158 |
|
x y D
27 11 6
61 13 22
94 11 73 |
|
x y D
6 4 2
34 24 2
14 8 3
52 30 3
7 3 5
18 8 5
47 21 5
10 4 6
98 40 6
16 6 7
34 12 8
38 12 10
20 6 11
14 4 12
52 15 12
11 3 13
30 8 14
62 16 15
66 16 17
34 8 18
18 4 20
23 5 21
48 10 23
98 20 24
52 10 27
16 3 28 |
|
x y D
27 5 29
22 4 30
34 6 32
46 8 33
70 12 34
74 12 38
50 8 39
38 6 40
26 4 42
20 3 44
47 7 45
96 14 47
100 14 51
51 7 53
30 4 56
62 8 60
66 8 68
25 3 69
34 4 72
52 6 75
79 9 77
83 9 85
56 6 87
38 4 90
48 5 92
29 3 93
78 8 95
98 10 96 |
|
x y D
85 38 5
73 22 11
48 11 19
85 19 20
73 11 44 |
| L=6 |
|
L=7 |
|
L=8 |
|
L=9 |
|
L=10 |
x y D
9 5 3
33 19 3
16 5 10
34 5 46
41 5 67 |
|
x y D
4 3 1
5 3 2
13 9 2
27 19 2
13 3 18
14 3 21
22 3 53
68 9 57
23 3 58 |
|
x y D
20 14 2
90 34 7
20 7 8
29 7 17
90 17 28
78 14 31
69 7 97 |
|
x y D
5 4 1
9 6 2
51 36 2
21 12 3
78 45 3
27 12 5
15 6 6
11 4 7
24 9 7
53 20 7
51 18 8
13 4 10
57 18 10
30 9 11
21 6 12
29 8 13
45 12 14
93 24 15
99 24 17
51 12 18
22 5 19
35 8 19
27 6 20
19 4 22
47 10 22
72 15 23 |
|
x y D
21 4 27
78 15 27
53 10 28
33 6 30
28 5 31
51 9 32
69 12 33
75 12 39
57 9 40
39 6 42
46 7 43
27 4 45
95 14 46
29 4 52
52 7 55
45 6 56
61 8 58
93 12 60
99 12 68
67 8 70
51 6 72
78 9 75
35 4 76
37 4 85
84 9 87
47 5 88
57 6 90
97 10 94 |
|
x y D
32 13 6
76 31 6
35 9 15
46 9 26 |
当HP読者のHN「k.nika」さんからの質問です。(平成24年10月11日付け)
ペル方程式 x2−Dy2=1 において、Dの値が100桁であっても多項式時間内で答えを
出す事は可能でしょうか?また、x2−Dy=1 において、Dの値のみから x、y を求める事
は可能でしょうか?
当HPがいつもお世話になっているHN「らすかる」さんからのコメントです。
(平成24年10月12日付け)
「国立情報学研究所ニュース 第19号」に、「特に、素因数分解、離散対数、ペルの方程式
については、古典の best-known のアルゴリズムはいずれも sub exponential time かかる
が、量子計算だと多項式時間で答えをだすことができる。」と書かれていますので、今のとこ
ろ無理っぽいです。
また、x2−Dy=1 について、y=D+2、x=D+1 が解の一つですね。
k.nika さんからのコメントです。(平成24年10月12日付け)
多項式時間内で可能であれば素因数分解に使えそうだったのですが、残念です。ありがと
うございした。
(追記) 令和3年4月25日付け
直角三角形の直角を挟む2辺の長さが1の場合を考える。
このような性質を持つ場合で、斜辺の長さが最も短いのは、(3,4,5)の直角三角形であ
る。
2番目に短いのは、 (20,21,29)の直角三角形
3番目に短いのは、 (119,120,169)の直角三角形
である。
4番目に短いのは、どんな直角三角形のときであろうか?
この問題の解決のために、ペル方程式の理論が活躍することを最近知ることが出来た。
任意の自然数 α>β に対して、ピタゴラス数は、次の3つの数の組で与えられる。
c=α2+β2 、 a=α2−β2 、 b=2αβ
このとき、 c2=a2+b2 が成り立つ。(→ 参考:「ヘロン数とピタゴラス数」)
整数 x、y に対して、 α=x+y 、β=y とおくと、
a=x2+2xy 、b=2y(x+y) 、c=x2+2xy+y2
と書ける。この整数 x、y は、次のペル方程式の解となる。
x2−2y2=±1
実際に、 a−b=x2+2xy−2y(x+y)=x2−2y2=±1 から明らかだろう。
ピタゴラス数が、ペル方程式により機械的に求められることに感動を覚える。
ペル方程式の理論によれば、方程式 x2−2y2=±1 のk番目の正の整数解(xk,yk)は、
(1+ )k=xk+yk
)k=xk+yk
により、求められる。
実際に、
k=1 のとき、 1+ =x1+y1
=x1+y1 より、 x1=1、y1=1
より、 x1=1、y1=1
このとき、 α=x1+y1=2 、β=y1=1 から、
c=α2+β2=5 、 a=α2−β2=3 、 b=2αβ=4
を得る。
k=2 のとき、 (1+ )2=3+2
)2=3+2 =x2+y2
=x2+y2 より、 x2=3、y2=2
より、 x2=3、y2=2
このとき、 α=x2+y2=5 、β=y2=2 から、
c=α2+β2=29 、 a=α2−β2=21 、 b=2αβ=20
を得る。
k=3 のとき、 (1+ )3=7+5
)3=7+5 =x3+y3
=x3+y3 より、 x3=7、y3=5
より、 x3=7、y3=5
このとき、 α=x3+y3=12、、β=y3=5 から、
c=α2+β2=169 、 a=α2−β2=119 、 b=2αβ=120
を得る。
k=4 のとき、 (1+ )4=17+12
)4=17+12 =x4+y4
=x4+y4 より、 x4=17、y4=12
より、 x4=17、y4=12
このとき、 α=x4+y4=29、、β=y4=12 から、
c=α2+β2=985 、 a=α2−β2=697 、 b=2αβ=696
を得る。
以下、工事中!
