微分方程式を解く方法として、いくつかの手法が知られている。
(1)
求積法
求積法により解ける微分方程式は数少ないが、微分方程式の概要をつかむには十分であ
ろう。その解法は、アクロバット的なところもあり、計算大好き人間にとってはたまらない魅力
があるといってもよく、「解けた!」という実感を存分に味わうことができる。
(2)
級数展開法
級数展開法は、解が整級数に展開されたものとして、その係数を未定係数法により決定し
て解を求める方法である。求積法で解ける微分方程式は、ごくまれで、ほとんどの場合解け
ない。そのようなとき、この級数展開法は有力な武器となる。
(3)
演算子法
演算子法は、ヘヴィサイドという電気工学の人が開発した方法で、主に電気工学関係の人
によく使われている。微分するということは微分演算子Dを掛けること、積分するということは
Dで割ることというように、数学の立場から言えば無茶苦茶な理論で、19世紀の終わり頃に
提唱された演算子法は、あまり顧みられなかった。しかし、その後、演算子法があまりに便
利だったため、数学的基礎付けをしようと多くの人が挑戦し、遂に1916年ブロムウィッチが
成功した。それため、また脚光を浴びることとなった。1929年ウィツタッカーによれば、
「19世紀最後の四半世紀における3つの最も重要な数学上の進歩として、
ポアンカレの保型関数の発見 リッチのテンソル解析の発見 ヘヴィサイドの演算子法の発見
をあげるべき」と述べている。
(4)
数値解析法
数値解析法は、解の関数値の表を、初期値から始めて次々と作っていく方法である。ただ、
この場合は誤差が入り込む余地があり、どの程度本当の解として信用できるかを考慮しな
ければならない。
(5)
線形微分方程式における常識的手段
線形微分方程式を解くうえで、必ず知っていなければいけないものがある。それは、
重ね合わせの原理・定数変化法・階数低下法
の3つである。
微分方程式を解く方法は、それぞれの特性に従って種々開発されていて枚挙にいとまが
ない。上で紹介した解法は、基本中の基本の解法であり、高校レベル〜大学初年級レベル
としては十分であろう。微分方程式の解のおおよそをつかむ方法として、次の「方向場」の
考えが、よく知られている。
1階の微分方程式 Y’=F(X、Y) の一つの解を Y=G(X) とする。XY平面上で、Y=G(X)
が表す曲線 C を、微分方程式の解曲線という。C上の任意の点P(X,Y) における接線の傾
きは、F(X、Y) に等しい。即ち、C上の任意の点 (X,Y) において、Cは、傾き m=F(X、Y)
の直線に接している。この性質を利用して、直線のかわりに微小線分を用いれば、平面上に
解曲線の方向を表す微小線分の分布が得られる。この分布を、微分方程式の
方向場という。
この方向場の様子を分析することにより、平面上の1点Pを指定すれば、解曲線で点Pを通
るものの存在が推察され、解曲線の全体像が浮かび上がってくる。
例1.微分方程式 Y’=Y/X の場合
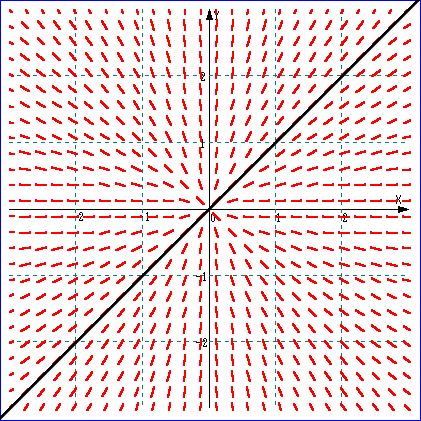 |
一般解は、Y=CX
(Cは任意定数)
左図においては、特殊解
直線 Y=X が、黒太実線
で示されている。
何とはなしに、この方向場
を眺めていると、
直線群 Y=CX が浮かび
上がってくると思う。 |
例2.微分方程式 Y’=Y の場合
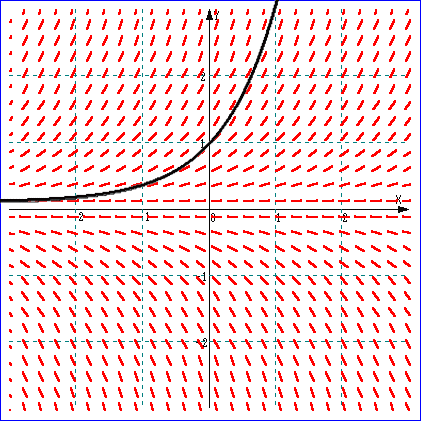 |
一般解は、Y=CeX
(Cは任意定数)
左図においては、特殊解
直線 Y=eX が、黒太
実線で示されている。
何とはなしに、この方向場
を眺めていると、
曲線群 Y=CeX が浮
かび上がってくると思う。 |
例3.微分方程式 Y’=1/X の場合
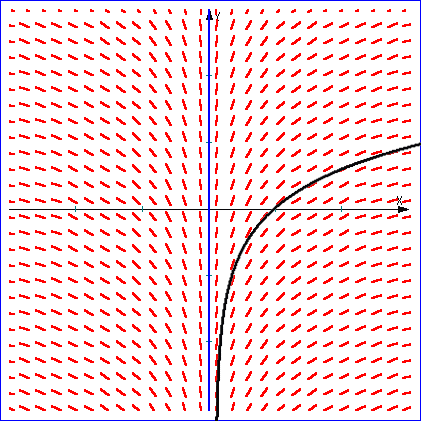 |
一般解は、Y=log CX
(Cは任意定数)
左図においては、特殊解
直線 Y=log X が、黒
太実線で示されている。
何とはなしに、この方向場
を眺めていると、
曲線群 Y=ClogCX が
浮かび上がってくると思う。 |



