(3)
演算子法・・・微分演算子を利用して、一般解を求める方法
関数 Y に対して、その導関数 Y’ を対応させる作用素Dを、微分演算子という。
(例1) 斉次線形1階微分方程式 Y’+αY=0 (αは定数) 即ち、(D+α)Y=0
の一般解は、

ただし、e は自然対数の底で、Cは任意定数
(例2) 線形1階微分方程式 Y’+αY=P (αは定数、PはXの関数) 即ち、
(D+α)Y=P の一般解は、
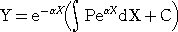
ただし、e は自然対数の底で、Cは任意定数
例2において、初期条件 Y=Y(0) のとき、次のように書き直すことができる。
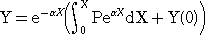
例題1 斉次線形2階微分方程式 Y’’’−4Y’=0 を、
初期条件 Y(0)=0、Y’(0)=1、Y”(0)=0 のもとで、求めよ。
(解) (D
3−4D)Y=0 より、D(D−2)(D+2)Y=0
このとき、解 Y は、DY=0、(D−2)Y=0、(D+2)Y=0 の解の一次結合
となる。例1 により、
Y=a+b
e2X+c
e-2X (a、b、c は任意定数)
と書ける。
初期条件から、 a+b+c=0、2b−2c=1、4b+4c=0 が成り立つので、
a=0、b=1/4、c=−1/4
したがって、求める解は、
Y=(1/4)
e2X−(1/4)
e-2X より、
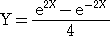
となる。
上記は、微分方程式の解の計算としては標準的である。これに対して、ヘヴィサイドは、
演算子法なるものを考え、次のように計算した。
積分演算子 L : F(X) →

の逆演算として、新しく微分演算子 B を、
B :

→ F(X) により、定める。このとき、L・B=B・L=1である。
Bの定義から分かるように、G(0)=0 となる関数に対しては、BG=G’=DG なので、
BとDは一致する。一般の関数G(X)に対しては、
G(X)=(G(X)−G(0))+G(0)
と考えることにより、
BG=G’(X)+BG(0)
となる。
(例3) 線形1階微分方程式 Y’+αY=P (αは定数、PはXの関数) において、
初期条件を Y(0)=0 とすれば、例2より、
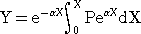
ここで、Y’+αY=P は、Y(0)=0 なので、(B+α)Y=P と書ける。
このとき、強引に、
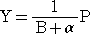
としてしまうのが、ヘヴィサイドの演算子法である。
先の計算結果により、次が成り立つ。
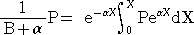
したがって、基本的な関数Pについて、右辺の計算結果の表を作っておけば、いちいち
積分しなくても、その表を用いれば、微分方程式が、単なる代数方程式として解けてしま
うというところが、ヘヴィサイドの演算子法のおいしいところである。
このヘヴィサイドの演算子法を用いて、例2を再度考えてみよう。
(例4) 線形1階微分方程式 Y’+αY=P (αは定数、PはXの関数) は、
BY−BY(0)+αY=P より、(B+α)Y=BY(0)+P と書き直せる。

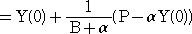
より、
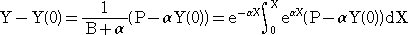
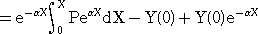
このことから、例2の式が導かれる。
例題2 斉次線形2階微分方程式 Y’’’−4Y’=0 を、
初期条件 Y(0)=0、Y’(0)=1、Y’’(0)=0 のもとで、求めよ。
(解) 演算子法により、求める。
Y’=BY−BY(0)=BY
Y”=BY’−BY’(0)=BY’−B=B
2Y−B
Y’’’=BY”−BY”(0)=BY”=B
3Y−B
2 なので、
与えられた微分方程式は、
B
3Y−B
2−4BY=0 すなわち、(B
3−4B)Y=B
2
よって、
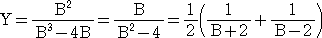
ここで、
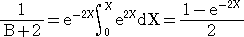
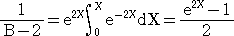
であるので、
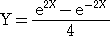
が、求める解となる。
例題1と例題2は、同じ問題であるが、解き方が違う。例題2の解き方の方が、スッキリして
いて、電気工学関係の人がヘヴィサイドの演算子法を好んだ理由が分かるような気がする。
しかし、この演算子法は、数学的裏付けがなく、19世紀の終わり頃に提唱された演算子法
は、数学の立場から、あまり顧みられなかった。しかし、演算子法があまりに便利だったため、
数学的基礎付けをしようと多くの人が挑戦し、遂に1916年ブロムウィッチが成功した。
ヘヴィサイドの演算子法は、ラプラス変換を用いて、その数学的な基礎付けがなされた。
これについては、ページをかえて、
7.ラプラス変換 で言及しようと思う。
