７．ラプラス変換　　　　　　　　　　　　　　　　　　　　

　大学初年級の数学の必修科目は、微分積分学と線形代数学であると、私は思う。そこで
学ぶ考え方は、実際に、それを使う使わないに関わらず、将来どんな方面に進むにせよ、
物事に対処する潜在能力になるものと信じる。

　今、大学では教養学部が解体され、早期に各自の専門学科を学ぶのが主流になってい
る。それは、いい面もあるのかもしれないが、視野の狭い教育になっていないか危惧する
所である。いろいろな雑学の中からこそ、新しい発想が生まれるのではないかと私は考え
る。

　物理学の方面では、既に「飛び級」制度が始まっているが、日本数学会では、「飛び級」
制度に反対していると聞く。私は、それに同調するものである。

　小学校入学以来学んできた算数・数学は、ただひたすらに微分・積分を目標としている。
それまで学んできたいろいろな事柄が、微分・積分の中で、互いに連関しあい、それまで
バラバラだった知識が一気に集約される。しかし、微分・積分までの険しい道の中で、多く
の人が美しい景色を見ることなく、ただ、「数学なんて〜」という恨み節を残して途中下車し
てしまっているのが現状だ。

　私自身、解析的代数幾何学を専攻としてきたが、未だに微分・積分の全貌をつかんで
はいない。そんな中で、私が美しい景色とうつったものが、このラプラス変換であり、関数
論における留数定理である。（実は、ラプラス逆変換の計算で、留数定理が利用される。）

　一般に、定積分計算は、原始関数を求める必要性から、微分に比べて、計算はしんど
い。しかし、関数論で留数定理を学ぶと、なぜか、「これって、ズルじゃない？」と思わずに
はいられない。積分することなく積分値が求まってしまうからだ。（詳しくは、こちらを参照）

　この留数定理で受けたショック以上のものを感じたのが、このページで紹介するラプラス
変換である。正直に告白すると、このラプラス変換の存在を知ったのは、実は、知り合いの
情報制御が専門の電気関係の方から、電気回路の微分方程式を解いて欲しいと頼まれ、
定数変化法などを用いて解いたのだが、「解き方として、こういう方法もあるよ！」というこ
とで紹介されたのが、このラプラス変換である。

　ラプラス変換対表というものがあって、この表を使えば、微分方程式の解は、難しい積分
計算をしなくても求まってしまうのだ！！

　この話を聞いて、留数定理で感じた以上に、「それって、ズルじゃない？」と思ったものだ。

　以下で、ラプラス変換について述べるが、このホームページの性格上、厳密性はある程
度無視して話を進めるつもりである。ラプラス変換の雰囲気を伝えることに徹したいと思う。

　ラプラス変換の定義

　　　関数　ｆ(ｔ) に対して、自然対数の底 ｅ と複素数 ｓ （ただし、ｓ の実部＞０）を用いて、

　　　　　

　　　　　（蛇足ながら、積分が収束するように、適切な　ｆ(ｔ)　を考える！）

　　で定まる Ｆ(ｓ) を、ｆ(ｔ) のラプラス変換といい、

　　　　　　　　Ｌ ：　ｆ(ｔ)　→　Ｆ(ｓ)

　　すなわち、　Ｌ（ｆ）＝Ｆ　と表す。

　　　ｓ のことを、ラプラス演算子（ラプラス変数）という。

（例）　ｆ(ｔ) ＝１　とする。このとき、

　　　　　　　

　　　　なので、１ のラプラス変換は、
　　　　　　　　　　　　　　　　　　　　　　　　

（例）　ｆ(ｔ) ＝ｔ　とする。このとき、

　　　　　　

　　　　なので、ｔ のラプラス変換は、
　　　　　　　　　　　　　　　　　　　　　　　　

　このことから、次のような対応表が考えられる。

	ｔ	→	１		１	→	ｔ		（実数の世界）
		微分				積分			（　ｓ　の世界）

　この対応表から、ラプラス変換の意味するところが、ぼんやりと分かる。

（１）　ｔ を微分すれば、１ だが、ｓ の世界では微分とは、どうも ｓ 倍のことらしい。


（２）　１を積分すれば、ｔ だが、ｓ の世界では積分とは、どうも ｓ で割ることらしい。

　以上の視点により、ヘヴィサイドの演算子法の数学的基礎付けとして、ラプラス変換が使
われたのだろう。

　今、 Ｆ(ｓ) を、ｆ(ｔ) のラプラス変換とする。部分積分の公式を用いて、ｆ(ｔ) の導関数 ｆ’(ｔ)
のラプラス変換　Ｌ（ｆ’）は、

　　　　　　　　　　　Ｌ（ｆ’）＝ｓＬ（ｆ）−ｆ（０）＝ｓＦ(ｓ)−ｆ(０)

となることが、直ぐ分かる。。

　（これは、演算子法で紹介した公式　Ｇ’（Ｘ）＝ＢＧ−ＢＧ（０）　と似ている！）

　さて、ラプラス変換は、ラプラス変換が一致したら、元の関数も一致するという重要な性質
を持つ。この性質を、ラプラス変換の単一性という。また、ラプラス変換は、線形性もあわ
せ持つ。これらの性質を利用して、微分方程式が、代数方程式を解くかのように鮮やかに
解かれる。

　例題に入る前に、基本的な関数に対して、ラプラス変換対表を掲げておこう。

　ラプラス変換を用いた解法　（演算子法で与えた解法と比較してみて下さい。）をいくつか
見ておこう。

例　題　　斉次線形１階微分方程式　Ｙ’−４Ｙ＝０　を、初期条件　Ｙ（０）＝１　のもとで求
　　　　　めよ。

　（解）　関数 Y　のラプラス変換を、Ｆ(ｓ) とする。

　　　このとき、Ｙ’ のラプラス変換は、ｓＦ(ｓ)−Ｙ(０)＝ｓＦ(ｓ)−１

　　　なので、与えられた微分方程式のラプラス変換は、

　　　　　　　　ｓＦ(ｓ)−１−４Ｆ(ｓ)＝０　すなわち、　（ｓ−４）Ｆ(ｓ)＝１

　　　よって、　Ｆ(ｓ)＝１/（ｓ−４）　となる。

　　　ラプラス変換の単一性とラプラス変換対表より、求める解は、

　　　　　　　　　　　Ｙ＝ｅ^4ｔ

　　　となる。　　（終）

例　題　　斉次線形２階微分方程式　Ｙ”＋４Ｙ＝０　を、初期条件　Ｙ（０）＝１ 、Ｙ’（０）＝０
　　　　　のもとで求めよ。

　（解）　関数 Y　のラプラス変換を、Ｆ(ｓ) とする。

　　　このとき、Ｙ’ のラプラス変換は、ｓＦ(ｓ)−Ｙ(０)＝ｓＦ(ｓ)−１　で、

　　　　　　　　Ｙ” のラプラス変換は、ｓ（ｓＦ(ｓ)−１）−Ｙ’（０）＝ｓ²Ｆ(ｓ)−ｓ

　　　なので、与えられた微分方程式のラプラス変換は、

　　　　　　　　ｓ²Ｆ(ｓ)＋４Ｆ(ｓ)＝ｓ　すなわち、　（ｓ²＋４）Ｆ(ｓ)＝ｓ

　　　よって、　Ｆ(ｓ)＝ｓ/（ｓ²＋４）　となる。

　　　ラプラス変換の単一性とラプラス変換対表より、求める解は、

　　　　　　　　　　　Ｙ＝ｃｏｓ２ｔ

　　　となる。　　（終）

例　題　　斉次線形３階微分方程式　Ｙ⁽³⁾−４Ｙ’＝０　を、
　　　　　初期条件　Ｙ（０）＝０ 、Ｙ’（０）＝１ 、Ｙ”（０）＝０　のもとで、求めよ。

　（解）　関数 Y　のラプラス変換を、Ｆ(ｓ) とする。

　　　このとき、Ｙ’ のラプラス変換は、ｓＦ(ｓ)−Ｙ(０)＝ｓＦ(ｓ)

　　　　　　　　　Ｙ” のラプラス変換は、ｓ（ｓＦ(ｓ)）−Ｙ’（０）＝ｓ²Ｆ(ｓ)−１

　　　　　　　　　Ｙ⁽³⁾ のラプラス変換は、ｓ（ｓ²Ｆ(ｓ)−１）−Ｙ”（０）＝ｓ³Ｆ(ｓ)−ｓ

　　　なので、与えられた微分方程式のラプラス変換は、

　　　　　　　　ｓ³Ｆ(ｓ)−ｓ−４（ｓＦ(ｓ)）＝０　すなわち、　（ｓ³−４ｓ）Ｆ(ｓ)＝ｓ

　　　よって、
　　　　　　　　　　　　　　


　　　ラプラス変換の単一性とラプラス変換対表より、求める解は、

　　　　　　　　　　　　　　

　　　となる。　　（終）

　この解答をみて、あなたも、「これって、ズルじゃない？」と思っていただけたら、私の安心
するところである。

　読者のために、練習問題を残しておこう。

練習問題　　斉次線形２階微分方程式　３Ｙ”−２Ｙ’−Ｙ＝０　を、
　　　　　　　初期条件　Ｙ（０）＝１ 、Ｙ’（０）＝０　のもとで求めよ。

　（Ｈｉｎｔ）　関数 Y　のラプラス変換を　Ｆ(ｓ) とすると、

　　　　　　　　　Ｆ(ｓ)＝（３ｓ−２）/（３ｓ²−２ｓ−１）

　　　　　となる。このとき、　Ｆ(ｓ)＝［３・｛１/（ｓ＋（1/3））｝＋１/（ｓ−１）］/４　なので、

　　　　　　　　　Ｙ＝｛３ｅ^(-1/3)ｔ＋ｅ^ｔ｝/２　・・・・　（出来たかな？）

（追記）　上記の例題では、ラプラス変換対表を用いて、一般解を求めたが、私的には、あ
　　　　　まり好ましい解法とはいえない。そのような場合、実は、計算によって求める方法
　　　　　が確立している。それが、ラプラス逆変換である。

　ラプラス変換では、関数 ｆ(ｔ) として、ｔ＜０ では、０ とし、ｔ＞０ でのみ考える。以下では、
すべて、ｔ＞０ として話を進める。

今、ラプラス変換 　　　　　　　 　　　　　に対して、 　　　　　　　 　　　　　を求めることを、ラプラス逆変換という。 　　　　　　右辺の積分は、複素積分で、その値 　　　　　の計算には、留数定理が用いられる。

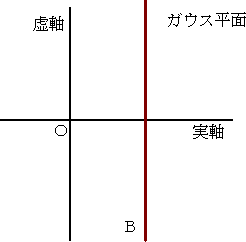　上記で、ｉ は虚数単位、Ｂ は、右上図のような虚軸に平行な積分路で、ブロムウィッチ‐
ワグナーの積分路といわれる。
　
　右辺の積分計算で、留数定理を使った計算に単純化するため、次の定理が利用される。

Ｊｏｒｄａｎ の補助定理

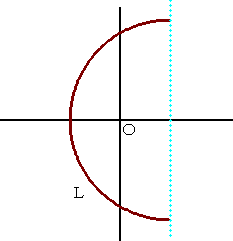
　　Ｆ(ｓ) は、｜ｓ｜→ ∞ で連続で、 ｓ → ∞ のとき、Ｆ(ｓ) → ０ とする。このとき、下図の
ような、半径Ｒの半円弧の積分路 Ｌ について、

が成り立つ。 　　（証明は、このホームページのレベル 　　　を超えるので　略） 　　このＪｏｒｄａｎ の補助定理により、 　ラプラス逆変換における積分路とし 　て、閉曲線が選択できることになり、 　その結果として、留数定理が使える 　ようになった、ということである。

　　　　　それでは、いくつかの場合について、ラプラス逆変換を計算してみよう。

　　　　（例） 以下の計算で、Ｃは、被積分関数の特異点をすべて含む閉曲線とする。

　　　　　　　　

　　　　　　　　　　　

　　　　　　　となる。

　　　　　　　　
　　　　　　　　　　　
　　　　　　　　　　　　　
　　　　　　　　　　　　　
　　　　　　　　　　　　　
　　　　　　　　　　　　　
　　　　　　　となる。

　　　　何れも、この計算結果は、前に示したラプラス変換対表のものと一致する。