（２）　級数展開法・・・微分方程式を級数を用いて解く方法
　　　微分方程式を級数を用いて解くといっても、ただ闇雲に級数を微分方程式に代入して解け
　　ば済むというほど、生易しい問題ではない。級数には、収束半径というものがあり、せっかく
　　求めた級数が解として意味を持たないということもありえる。
　　　したがって、ここではいくらか予備知識を確認しなければならない。
　　
　　ΣＣ_ｎ(Ｘ−ａ)^ｎ　（ｎ＝０，１，・・・） の形の級数を、整級数という。

　　整級数　ΣＣ_ｎ(Ｘ−ａ)^ｎ　（ｎ＝０，１，・・・）　が、あるＸの値で有限確定値になるとき、
　そのＸの値で、整級数は収束するという。収束しないとき、発散するという。

　　整級数　ΣＣ_ｎ(Ｘ−ａ)^ｎ　（ｎ＝０，１，・・・） において、
　　　　｜Ｘ−ａ｜＜Ｒ　の範囲で収束、｜Ｘ−ａ｜＞Ｒの範囲で発散
　であるとき、整級数の収束半径は、Ｒであるという。

　　収束半径の計算については、次の Cauchy-Hadamard の定理が知られている。

　定理　　整級数　ΣＣ_ｎ(Ｘ−ａ)^ｎ　（ｎ＝０，１，・・・）　において、その収束半径Ｒは、次の式で
　　　　　与えられる。

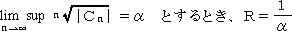または

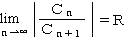　　　（注意）　上記の計算で、lim sup　を上極限という。
　　　　　上極限の計算については、次の例題で感覚を理解してください。

（例題）　ａ_ｎ＝(−１）^ｎ(１＋１/ｎ)　について、上極限、下極限を求めよ。

　　　　　　　　　　　（答）　lim sup ａ_ｎ＝１、lim inf ａ_ｎ＝−１

　練習　次の整級数の収束半径を求めよ。
　　　　（１）　ΣＸ^ｎ　（ｎ＝０，１，・・・）
　　　　（２）　Σ(１/ｎ)Ｘ^ｎ　（ｎ＝０，１，・・・）
　　　　（３）　Σ(１/ｎ！)Ｘ^ｎ　（ｎ＝０，１，・・・）
　　　　　　　　　　　　　　　　　　　　　　　　　　　（答）（１）　Ｒ＝１　（２）　Ｒ＝１　（３）　Ｒ＝＋∞

　　関数が正則（または解析的）ということ
　　　関数 Ｆ(Ｘ) が、Ｘ＝ａ の近くで、
　　　　　　　　　　　　Ｆ(Ｘ)＝ΣＣ_ｎ(Ｘ−ａ)^ｎ　（ｎ＝０，１，・・・）
　　と表され、その収束半径が０ではないとき、関数 Ｆ(Ｘ) は、Ｘ＝ａ の近くで正則であるという。

　　微分方程式　Ｙ”＋ＰＹ’＋ＱＹ＝Ｒ　において、
　　　　Ｐ、Ｑ、Ｒ　が正則であるような点　Ｘ＝ａ　を、微分方程式の通常点といい、
　　　その他の点を、特異点という。

　　通常点、特異点では利用する級数の形が異なる。特異点については、さらなる分類があり、
　非常に難しい議論が待っている。したがって、このページでは、通常点のみを考えることにする。

　　このとき、次の定理は有名である。

　定理（コーシーの定理）
　　　微分方程式　Ｙ”＋ＰＹ’＋ＱＹ＝Ｒ　において、
　　Ｐ、Ｑ、Ｒが、Ｘ＝ａ の近くで正則ならば、微分方程式の解もＸ＝ａ の近くで正則である。

　通常点においては、この定理のおかげで、安心して微分方程式を級数展開して求めることが
できる。

　例題　微分方程式　Ｙ’＝Ｘ＋２ＸＹ　を解け。

　　　関数　Ｘ、２Ｘ　は、Ｘ＝０　の近くで正則なので、コーシーの定理により、微分方程式の解も
　　Ｘ＝０　の近くで、正則である。
　　　今、Ｙ＝Ｃ_０＋Ｃ_１Ｘ＋Ｃ_２Ｘ^２＋Ｃ_３Ｘ^３＋・・・＋Ｃ_ｎＸ^ｎ＋・・・　とおくと、
　　　　　　　 Ｙ’＝Ｃ_１　　＋２Ｃ_２Ｘ＋３Ｃ_３Ｘ^２＋・・・＋ｎＣ_ｎＸ^ｎ−１＋・・・　で、
　　　　Ｘ＋２ＸＹ＝　　(１＋２Ｃ_０)Ｘ＋２Ｃ_１Ｘ^２＋・・・＋２Ｃ_ｎＸ^ｎ＋１＋・・・　なので、
　　係数を比較して、
　　　　Ｃ_１＝０、２Ｃ_２＝１＋２Ｃ_０、３Ｃ_３＝２Ｃ_１、・・・、ｎＣ_ｎ＝２Ｃ_ｎ−２　が成り立つ。
　　よって、
　　　　Ｃ_０＝Ｃ_２−１/２、Ｃ_３＝０、Ｃ_４＝(１/２)Ｃ_２、Ｃ_５＝０、Ｃ_６＝(１/３)Ｃ_４＝(１/３！)Ｃ_２、・・・
　　したがって、求める解は、
　　　　　　Ｙ＝Ｃ_２(１＋Ｘ^２＋(１/２！)Ｘ^４＋(１/３！)Ｘ^６＋・・・　）　　　（ただし、Ｃ_２は任意定数）
　　この整級数の収束半径は、明らかに、＋∞　である。

　（注意）　指数関数　Ｆ(Ｘ)＝ｅ^Ｘ　のマクローリン展開：
　　　　　　　ｅ^Ｘ＝１＋Ｘ＋(１/２！)Ｘ^２＋(１/３！)Ｘ^３＋・・・
　　を知っていれば、上記の解は、簡単に、
　　　　　　　　　　
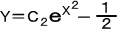
　　と書ける。