（１）
求積法・・・不定積分を有限回行うことによって一般解を求める方法
与えられた１階微分方程式のタイプにより、解法には３つのパターンがある。
（イ） 変数分離形・・・Ｙ’＝Ｆ(Ｘ)Ｇ(Ｙ)のタイプ
例 Ｙ’＝Ｙ/Ｘ
(１/Ｙ)Ｙ’＝１/Ｘ の形に変形し、両辺の不定積分を求めればよい。
一般解は、Ｙ＝ＣＸ （Ｃは任意定数）
（ロ） 同次形・・・Ｙ’＝Ｆ(Ｙ/Ｘ)のタイプ
例 Ｙ’＝Ｙ/Ｘ
Ｙ/Ｘ＝Ｚとおくと、Ｙ＝ＸＺ 両辺をＸで微分して、Ｙ’＝Ｚ＋ＸＺ’
よって、Ｚ＋ＸＺ’＝Ｚより、ＸＺ’＝０ ゆえに、Ｚ’＝０
したがって、Ｚ＝Ｃ （Ｃは任意定数）より、一般解は、Ｙ＝ＣＸ
（ハ） 線形・・・Ｙ’＋ＰＹ＝Ｑ （Ｐ、ＱはＸの関数）のタイプ
一般解は、
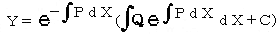
ただし、ｅ は自然対数の底で、Ｃは任意定数
（略証） Ｑ＝０ として微分方程式を解き、そのときの任意定数をＸの関数とみなして、与え
られた微分方程式に代入する。任意定数に関する微分方程式を解き、その解を求めれば、
公式を得ることができる。（このような解法を、定数変化法といい、最初に応用した人は、
Jacques Bernoulli である。）
例 Ｙ’＋Ｙ＝Ｘ
一般解は、Ｙ＝Ｘ−１＋Ｃ
ｅ−Ｘ （Ｃは任意定数）
上記のパターン以外に、求積法により解くことができる微分方程式としては、Jean Bernoulli
の微分方程式（（ハ）におけるＱがＱＹ
ｎの形で、Ｚ＝Ｙ
１−ｎとおけばよい）、Riccati の微分方程
式（求積法では解けないが、一つの特殊解が求まれば、求積法により解くことができる）、
Clairaut の微分方程式およびその一般化されたLagrange の微分方程式 等々あるが、興味
をもたれた方は、是非専門書にあたられたい。
高階の微分方程式については、次の例をあげるにとどめる。ニュートンの運動方程式を解
くには十分であろう。
例 Ｙ”＝Ｙ
両辺に、２Ｙ’を掛けることが、定石である。２Ｙ’Ｙ”＝２ＹＹ’ より （Ｙ’
２）’＝（Ｙ
２）’から、
Ｙ’
２＝Ｙ
２＋Ｃ
両辺の平方根を求め、後は１階の微分方程式の解法に従えばよい。
（以下の解答は省略するが、Ｙ＋√(Ｙ
２＋Ｃ)＝ｔ と置くタイプの置換積分を駆使するなど相当
な計算力を要する。）
上記の例のような微分方程式では上のように解くということを学んで以来、それ以外の解
答については、あまり深く考えることはなかったが、下記のような驚くべき別解があるので、
紹介したい。非常に技巧的で、惚れ惚れしてしまう（と思う）！
例 Ｙ”＝Ｙ
Ｖ＝−Ｙ’(
ｅｘ−
ｅ-ｘ)＋Ｙ(
ｅｘ＋
ｅ-ｘ) 、Ｗ＝Ｙ’(
ｅｘ＋
ｅ-ｘ)−Ｙ(
ｅｘ−
ｅ-ｘ) とおく。
このとき、Ｖ’＝−Ｙ”(
ｅｘ−
ｅ-ｘ)−Ｙ’(
ｅｘ＋
ｅ-ｘ)＋Ｙ’(
ｅｘ＋
ｅ-ｘ)＋Ｙ(
ｅｘ−
ｅ-ｘ)＝０
Ｗ’＝Ｙ”(
ｅｘ＋
ｅ-ｘ)＋Ｙ’(
ｅｘ−
ｅ-ｘ)−Ｙ’(
ｅｘ−
ｅ-ｘ)−Ｙ(
ｅｘ＋
ｅ-ｘ)＝０
よって、Ｖ、Ｗは定数である。ところで、
Ｖ(
ｅｘ＋
ｅ-ｘ)＋Ｗ(
ｅｘ−
ｅ-ｘ)＝Ｙ(
ｅｘ＋
ｅ-ｘ)
２−Ｙ(
ｅｘ−
ｅ-ｘ)
２＝４Ｙ
ここで、（Ｖ＋Ｗ）/４＝Ａ、（Ｖ−Ｗ）/４＝Ｂ とおくと、
Ｙ＝Ａ
ｅｘ＋Ｂｅ-ｘ （Ａ、Ｂは任意定数）
となる。（俣野 博 氏（東京大学）による解答）
（注意） 微分方程式を求積法で解くにあたり、気になる点がある。例えば、微分方程式
Ｙ’＝Ｙ において、両辺をＹで割るときである。
小学校以来、０で割ってはいけないと繰り返し言われてきた人なら、なおさらであろう。Ｘの
ある瞬間 Ｙが０になって、そのとき割っていいものか、悩む人は多い。
これに関して、その悩みを打破するような有名な解答が存在する。
まず、微分方程式 Ｙ’＝Ｙ は、通常、次のように解かれる。
Ｙ≡０ は解である。
Ｙ≠０ のときは、求積法により、Ｙ＝Ｃ
ｅｘ （Ｃは、０と異なる任意定数） である。
ここで、Ｙ≡０ は、Ｃ＝０ とすればよいから、求める一般解は、
Ｙ＝Ｃ
ｅｘ （Ｃは任意定数） となる。
ここで、あるＸに対して、Ｙ＝０ という場合が起こらないことは、次のようにして納得される。
微分方程式 Ｙ’＝Ｙ の一つの解を Ｙ
１ とし、ｕ＝
ｅ-ｘＹ
１ とおく。
このとき、明らかに ｕ’＝０ なので、ｕ＝Ｃ （Ｃは任意定数） となる。
よって、 Ｙ
１＝Ｃ
ｅｘ （Ｃは任意定数）
ゆえに、Ｃ＝０ ならば、Ｙ
１≡０ であり、Ｃ≠０ ならば、あるＸで Ｙ
１＝０ ということは起
こりえない。
ここら辺の議論は、実は解の一意性の議論とも関係していて、難しい面がある。高等学校
程度の、ごく初歩的な段階では、あまり神経質にならないほうが得策かもしれない。
（追記） 令和６年８月８日付け
実際の大学入試問題で、微分方程式を解く問題を考察しておこう。
（１９９６年までの学習指導要領にあった「微分方程式」が、１９９７年〜２００５年の学習指導
要領で消滅したが、２００６年〜の学習指導要領では若干復活した。ただ、変数分離形程度
に止まり、往年の微分方程式とはほど遠い。理工系にとっては重要な概念なので、学校で教
わらなくても身に付けておきたいところだ。）
東北大学 理系（１９７７）で、次の問題が出題された。
第５問 ４００Ｌの水が入っている水槽がある。はじめに排水口を閉じたまま、この水槽に
１Ｌにつき０．２ｋｇの塩を含む塩水を、毎分１０Ｌの割合で注ぐ。このように塩水を注ぎ続
けながら、１０分後からは排水口をあけて毎分１０Ｌの割合で混合液を流出させる。
ただし、水槽内の塩水の濃度はつねに一様に保たれており、混合液は水槽からあふれな
いものとする。
（１） 塩水を注ぎはじめてから ｔ 分後の水槽内の塩の量を ｘ ｋｇとする。そのとき塩水の濃
度(ｋｇ/Ｌ)を ｔ と ｘ を用いて表せ。
（２） 塩水を注ぎはじめてから１時間後の水槽内の塩の量はいくらか。
（解）（１） ０≦ｔ≦１０ のとき、濃度は、 １００ｘ/（４００＋１０ｔ） （％）
ｔ≧１０ のとき、濃度は、 １００ｘ/５００＝ｘ/５ （％）
（２） １時間後の水槽内の塩の量が問題なので、 ｔ≧１０ としてよい。
入ってくる塩の量は、１分あたり、 ０．２×１０＝２（ｋｇ）
出ていく塩の量は、１分当たり、 １０×（ｘ/５）÷１００＝ｘ/５０（ｋｇ）
このとき、ｄｘ/ｄｔ＝２−ｘ/５０＝−（ｘ−１００）/５０ より、 ｄｘ/（ｘ−１００）＝−ｄｔ/５０ より、
ｌｏｇ｜ｘ−１００｜＝−（１/５０）ｔ＋Ｃ
よって、 ｘ−１００＝±ｅ＾Ｃ・ｅ＾（−（１/５０）ｔ）
ここで、 ±ｅ＾Ｃ を改めてＣとおくと、 ｘ＝１００＋Ｃｅ＾（−（１/５０）ｔ）
ｔ＝１０ のとき、ｘ＝２０ なので、 ２０＝１００＋Ｃｅ＾（−１/５） より、Ｃ＝−８０ｅ＾（１/５）
したがって、 ｘ＝１００−８０ｅ＾（１/５−（１/５０）ｔ） となる。
このとき、１時間後の水槽内の塩の量は、ｔ＝６０ を代入して、
ｘ＝１００−８０ｅ＾（−１）＝１００−８０/ｅ （終）
（コメント） 排水しなければ、１時間後の塩の量は１２０ｋｇになるのだが、排水したせいで、
塩の量は７０ｋｇ程度に収まるんですね！
（追記） 令和６年９月２日付け
東北大学 理系（１９７９）で、次の問題が出題された。
第６問 底面の半径 ｒ の直円柱のタンクに、高さ ｈ まで水が入っているとする。今タンク
の底に亀裂が生じ、水もれが起こったとする。流出する水量の速さは水面の高さに比例
し、１時間後には全体のα％が流出したとする。ｔ 時間後にタンクに残っている水量はい
くらか。
（解） ｔ 時間後の水の高さを ｘ とすると、そのときの水量は、 πｒ
2ｘ
このとき、流出する水量の速さは、πｒ
2・ｄｘ/ｄｔ で、題意より、
πｒ
2・ｄｘ/ｄｔ＝ｋｘ （ｋは定数） とおける。
よって、 πｒ
2・ｌｏｇ ｘ ＝ｋｔ＋Ｃ （Ｃは任意定数） となる。
ｔ＝０ のとき、ｘ＝ｈ より、 Ｃ＝πｒ
2・ｌｏｇ ｈ と書けるので、 πｒ
2・ｌｏｇ ｘ/ｈ ＝ｋｔ
ｔ＝１ のときの水の高さを ｘ
0 とすると、題意より、 πｒ
2（ｈ−ｘ
0）＝πｒ
2ｈ（α/１００）
よって、 ｘ
0＝（１−α/１００）ｈ と書けるので、 ｋ＝πｒ
2・ｌｏｇ（１−α/１００）
以上から、 ｌｏｇ ｘ/ｈ ＝ｔ・ｌｏｇ（１−α/１００） より、
ｘ/ｈ＝（１−α/１００）
ｔ すなわち、 ｘ＝ｈ・（１−α/１００）
ｔ
したがって、ｔ 時間後にタンクに残っている水量は、
πｒ
2ｈ・（１−α/１００）
ｔ （終）
（コメント） １時間後には全体のα％が流出することから、
１時間後のタンクに残っている水量は、 πｒ
2ｈ・（１−α/１００）
２時間後のタンクに残っている水量は、
πｒ
2ｈ・（１−α/１００）・（１−α/１００）＝πｒ
2ｈ・（１−α/１００）
2
・・・・・・・・・・・・・・・・・
ｔ 時間後のタンクに残っている水量は、 πｒ
2ｈ・（１−α/１００）
ｔ
と考えた方が素直かな？
（追記） 令和６年９月１２日付け
東北大学 理系（１９８０）で、次の問題が出題された。
第６問 Ｆ（ｘ）は、ｘ≧０ で定義された連続関数で、条件
Ｆ（１）＝Ｆ’（１）＝０、Ｆ”（ｘ）＞０ （ｘ＞０）
を満たすとする。曲線 C ： ｙ＝Ｆ（ｘ） 上の点(ｘ ，Ｆ（ｘ）) (ｘ＞０) におけるCの接線と曲線Cお
よび ｙ 軸とで囲まれる部分の面積が ｘ
3ｅ
ｘ になるという。関数Ｆ（ｘ）を求めよ。
（解） 曲線 C ： Ｙ＝Ｆ（Ｘ） 上の点(ｘ ，Ｆ（ｘ）) におけるCの接線の方程式は、
Ｙ＝Ｆ’（ｘ）（Ｘ−ｘ）＋Ｆ（ｘ） である。
Ｆ”（ｘ）＞０ （ｘ＞０）より、ｘ＞０ において、Ｆ（ｘ）は下に凸である。
題意より、 ｘ
3ｅ
ｘ＝∫
0x （Ｆ（Ｘ）−Ｆ’（ｘ）（Ｘ−ｘ）−Ｆ（ｘ））ｄＸ
すなわち、 ｘ
3ｅ
ｘ＝∫
0x Ｆ（Ｘ）ｄＸ−Ｆ’（ｘ）（ｘ
2/２）＋ｘ
2Ｆ’（ｘ）−ｘＦ（ｘ）
両辺を ｘ で微分して、
（ｘ
3＋３ｘ
2）ｅ
ｘ＝Ｆ（ｘ）−Ｆ”（ｘ）（ｘ
2/２）−ｘＦ’（ｘ）＋２ｘＦ’（ｘ）＋ｘ
2Ｆ”（ｘ）−Ｆ（ｘ）−ｘＦ’（ｘ）
すなわち、 （ｘ
3＋３ｘ
2）ｅ
ｘ＝Ｆ”（ｘ）（ｘ
2/２） より、 Ｆ”（ｘ）＝（２ｘ＋６）ｅ
ｘ
よって、 Ｆ’（ｘ）＝（２ｘ＋４）ｅ
ｘ＋Ｃ （Ｃは積分定数） において、
Ｆ’（１）＝６ｅ＋Ｃ＝０ より、 Ｃ＝−６ｅ
よって、 Ｆ’（ｘ）＝（２ｘ＋４）ｅ
ｘ−６ｅ より、
Ｆ（ｘ）＝（２ｘ＋２）ｅ
ｘ−６ｘｅ＋Ｄ （Ｄは積分定数） において、
Ｆ（１）＝−２ｅ＋Ｄ＝０ より、 Ｄ＝２ｅ
以上から、 Ｆ（ｘ）＝（２ｘ＋２）ｅ
ｘ−６ｘｅ＋２ｅ＝２（ｘ＋１）ｅ
ｘ−２（３ｘ−１）ｅ （終）
（追記） 令和６年９月２２日付け
次の東北大学 理系（１９８１）の問題は、まず微分方程式を作って解くというタイプの問題
である。
問題３ 放物線 ｙ＝ｘ
2 上を動く点Ｐがあって、時刻 ｔ＝０ のときの位置は原点である。また、
時刻 t のとき、Ｐの速度ベクトルの ｘ 成分は、ｓｉｎ ｔ である。速度ベクトルの ｙ 成分が最
大となるときのPの位置を求めよ。また、そのときにおけるPの速度ベクトルおよび加速度
ベクトルを求めよ。
（解） Ｐ（ｘ，ｘ
2）において、題意より、 ｄｘ/ｄｔ＝ｓｉｎ ｔ より、 ｘ＝−ｃｏｓ ｔ ＋Ｃ
ｔ＝０ のとき、ｘ＝０ より、 Ｃ＝１ なので、 ｘ＝１−ｃｏｓ ｔ
このとき、速度ベクトルの ｙ 成分は、 ２ｘ・ｄｘ/ｄｔ＝２ｓｉｎ ｔ （１−ｃｏｓ ｔ ）
よって、 ｖ＝２ｓｉｎ ｔ （１−ｃｏｓ ｔ ） とおくと、
ｖ’＝２ｃｏｓ ｔ （１−ｃｏｓ ｔ ）＋２ｓｉｎ
2 ｔ ＝２ｃｏｓ ｔ −２ｃｏｓ
2 ｔ ＋２−２ｃｏｓ
2 ｔ
＝−４ｃｏｓ
2 ｔ ＋２ｃｏｓ ｔ ＋２＝−２（２ｃｏｓ ｔ ＋１）（ｃｏｓ ｔ −１）＝０ を解くと、
０≦ｔ≦２π において、 ｔ ＝２π/３ 、４π/３ 、０ 、２π
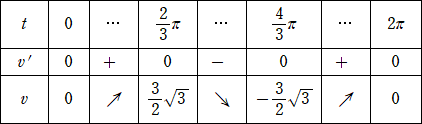
増減表より、ｔ＝２π/３ で、ｖ は極大かつ最大となる。
このとき、ｘ＝３/２ より、Ｐ（３/２，９/４） である。
Pの速度ベクトルは、（−
/２，３
/２） で、
（ｓｉｎ ｔ ）’＝ｃｏｓ ｔ ＝−１/２ 、ｖ’＝０
から、Pの加速度ベクトルは、（−１/２，０） となる。 （終）
（追記） 令和６年１０月１日付け
次の東北大学 理系（１９８１）の問題も微分方程式を解く問題である。
問題６ 平面上を運動する点Pの座標(ｘ，ｙ)が時刻 ｔ のとき、ｘ＝Ｆ(ｔ)sin ｔ、ｙ＝Ｆ(ｔ)cos ｔ で
表されている。Ｐは t＝０ のとき、(０，１)にあり、ｔ が限りなく大きくなるとき原点 (０，０)に
近づき、時刻 ｔ における速さは、２Ｆ(ｔ)に等しいという。
（１） 関数Ｆ(ｔ)を求めよ。
（２） 時刻 ０ から時刻 ａ までの間に、点Ｐが動く道のりを求めよ。ただし、ａ＞０ とする。
（解）（１） ｘ’＝Ｆ’(ｔ)sin ｔ＋Ｆ(ｔ)cos ｔ 、ｙ’＝Ｆ’(ｔ)cos ｔ−Ｆ(ｔ)sin ｔ より、
（ｘ’）
2＋（ｙ’）
2＝（Ｆ’(ｔ)sin ｔ＋Ｆ(ｔ)cos ｔ）
2＋（Ｆ’(ｔ)cos ｔ−Ｆ(ｔ)sin ｔ）
2＝（Ｆ’(ｔ)）
2＋（Ｆ(ｔ)）
2
よって、条件より、 （Ｆ’(ｔ)）
2＋（Ｆ(ｔ)）
2＝４（Ｆ(ｔ)）
2 すなわち、 （Ｆ’(ｔ)）
2＝３（Ｆ(ｔ)）
2
Ｆ’(ｔ)＝±
Ｆ(ｔ) から、 Ｆ’(ｔ)/Ｆ(ｔ)＝±
なので、 ｌｏｇ｜Ｆ(ｔ)｜＝±
ｔ
すなわち、 Ｆ(ｔ)＝Ｃ・ｅ＾（±
ｔ） となる。
ここで、Ｆ(０)＝１ なので、 Ｃ＝１ より、 Ｆ(ｔ)＝ｅ＾（±
ｔ）
ｔ が限りなく大きくなるとき原点 (０，０)に近づくので、Ｆ(ｔ)＝ｅ＾（
ｔ）は不適。
以上から、 Ｆ(ｔ)＝ｅ＾（−
ｔ）
（２） （ｘ’）
2＋（ｙ’）
2＝４ｅ＾（−２
ｔ） なので、求める道のりは、
∫
0a ２ｅ＾（−
ｔ）ｄｔ＝[−（２/
）ｅ＾（−
ｔ）]
0a＝（２/
）（１−ｅ＾（−
ａ）） （終）
（追記） 令和６年１０月２４日付け
次の東北大学 理系（１９８３）の問題は、解法のヒントが与えられている。
問題６ P(ｘ，ｙ)は第１象限を ｙ 座標が増加する方向に動く点で、時刻 ｔ のとき、その位置
は、 ｘ＝４−２Ｆ（ｔ） 、ｙ＝Ｆ（ｔ） で与えられ、その速さは ｘｙ に等しいという。
（１） Ｆ（ｔ）の満たす微分方程式を求めよ。また、Ｇ（ｔ）＝１/Ｆ（ｔ） とおいたとき、Ｇ（ｔ）の満た
す微分方程式を求めよ。
（２） 時刻 ｔ＝０ におけるPの座標が(２，１)であるとして、Ｆ（ｔ）を求めよ。
（３） （２）において、ｔ → ∞ のとき、Pはどのような点に近づくか。
（解）（１） ｘ’＝−２Ｆ’（ｔ） 、ｙ’＝Ｆ’（ｔ） より、 （ｘ’）
2＋（ｙ’）
2＝５（Ｆ’（ｔ））
2
よって、速さは、
Ｆ’（ｔ）＝（４−２Ｆ（ｔ））Ｆ（ｔ） となる。
Ｇ（ｔ）＝１/Ｆ（ｔ） より、 Ｇ’（ｔ）＝−Ｆ’（ｔ）/Ｆ
2（ｔ） なので、 −
Ｇ’（ｔ）＝４Ｇ（ｔ）−２
（２） Ｇ’（ｔ）/（４Ｇ（ｔ）−２）＝−１/
より、 （１/４）ｌｏｇ｜４Ｇ（ｔ）−２｜＝−ｔ/
＋Ｃ
ｔ＝０ のとき、 Ｆ（０）＝１ なので、 Ｇ（０）＝１ より、 Ｃ＝（１/４）ｌｏｇ２
よって、 ｌｏｇ｜２Ｇ（ｔ）−１｜＝−４ｔ/
より、 ２Ｇ（ｔ）−１＝±ｅ＾（−４ｔ/
）
Ｇ（０）＝１ より、２Ｇ（ｔ）−１＝ｅ＾（−４ｔ/
） すなわち、 Ｇ（ｔ）＝（１＋ｅ＾（−４ｔ/
））/２
以上から、 Ｆ（ｔ）＝２/（１＋ｅ＾（−４ｔ/
））
（３） ｔ → ∞ のとき、ｅ＾（−４ｔ/
） → ０ なので、 Ｆ（ｔ） → ２
よって、 Ｐ → （０，２） に近づく。 （終）
以下、工事中！