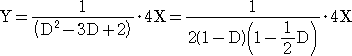(5)
線形微分方程式における常識的手段
以下では、簡単のため、定数係数2階線形常微分方程式について、話を進める。
微分方程式 aY”+bY’+cY=P において、微分演算子Dを用いれば、
(aD2+bD+c)Y=P
と書ける。このとき、微分作用素 L=aD
2+bD+c のことを、
微分多項式という。
今、LY=0 を満たす解の全体を、Vとおくと、Vは、2次元のベクトル空間となる。すな
わち、一次独立な解として、2つの関数 Y、Z を適当にとると、Vに属する任意の関数
は、その一次結合(aY+bZの形)で表せる。
(例) Y”+5Y’+6Y=0 において、L=D
2+5D+6 とおくと、 LY=0
このとき、
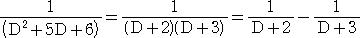
が成り立つ(部分分数分解)ので、分母を払って、 1 = (D+3)−(D+2)
LY=0 を満たす解を、Y とすると、
Y = 1・Y = ((D+3)−(D+2))Y = (D+3)Y−(D+2)Y
そこで、Y
1=(D+3)Y、Y
2=−(D+2)Y とおくと、Y=Y
1+Y
2 と書ける。
このとき、(D+2)Y
1=LY=0 より、Y
1 は、微分方程式 (D+2)Y=0 の解となる。
同様にして、Y
2 は、微分方程式 (D+3)Y=0 の解となる。
(D+2)Y=0 の解は、a
e-2x 、 (D+3)Y=0 の解は、b
e-3x
以上から、 LY=0 の一般解は、
Y=a
e-2x+b
e-3x (a、b は定数)
と書ける。
上の例について、面白い解法がある。
LY=0 の解として、Y=
eλx の形の関数を考える。このとき、λは、
λ
2+5λ+6=0
を満たす。(この方程式を、
特性方程式という。)
(
この特性方程式の左辺は、ちょうど、D=λ のときのLの値になっている。)
2次方程式を解くと、λ=−2、−3 なので、L(Y)=0 は、特殊解
e-2x 、
e-3x を持
つことが直ぐ分かる。
このとき、次の定理を用いて、一般解 Y=a
e-2x+b
e-3x が得られる。
定理A 微分方程式 LY=0 の特性方程式の2つの解を、α、β とおく。
このとき、一般解は、次の形で与えられる。(但し、a、b は定数)
実数α、β に対して、α≠β のとき、Y=aeαx+beβx
実数α、β に対して、α=β のとき、Y=aeαx+bXeαx
虚数解α、β(=m±ni) に対して、Y=emx(a・cos nx+b・sin nx)
(例題) 微分方程式 Y”+Y=0 を解け。
積分因子を用いる解法では次のように解かれるだろう。
(解) Y”+Y=0 の両辺に積分因子 2Y’ を掛けて、 2Y’Y”=−2YY’
(Y’
2)’=−(Y
2)’ なので、 Y’
2=−Y
2+C (Cは任意定数)
すなわち、
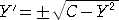
より、Dを任意定数として、

ここで、
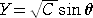
と置換すると、
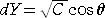
なので、
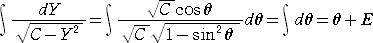
ただし、Eは任意定数で、 F=D−E とおくと、
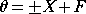
よって、
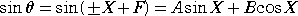
より、
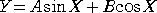
(A、Bは任意定数)
と書ける。(終)
このことから、特性解を用いた解法で解が次のように解かれることも理解できるだろう。
(解) Y”+Y=0 の特性方程式は、 λ
2+1=0 で、 虚数解 λ=±i を持つ。
よって、求める一般解は、 Y=a・cos X+b・sin X (
a 、 b は任意定数)
上記の積分因子による計算で、積分計算をしないで一般解を求める方法も知られている。
( →
こちらを参照)
さらに、次の定理が成り立つ。
定理B LY=P の特殊解を、Y1 、LY=0 の一般解を、Y2 とすると、
LY=P の一般解は、Y1+Y2 で与えられる。
定理Bによれば、何らかの手段で、LY=P の特殊解を求めれば、上の定理Aを用いて、
LY=P の一般解が求められることになる。
LY=P の特殊解を求める方法
L=aD
2+bD+c において、F(D)=aD
2+bD+c とする。LY=P の特殊解を求める
場合、次の公式が用いられる。
定理
定理 LY=P (P:多項式)の特性方程式 F(X)=0 の解 0 の重複度を、n とす
る。このとき、LY=P は、XnQ (Qは、Pと同じ次数の多項式)の形の特殊解を
持つ。
(例題1) 微分方程式 Y”−3Y’+2Y=4X の特殊解を求めよ。
(解) 特性方程式 X
2−3X+2=0 は、0 を解に持たないから、重複度は、0
よって、定理より、特殊解として、AX+B の形の特殊解をもつ。
これを微分方程式に代入して、 0−3・A+2(AX+B)=2AX+2B−3A=4X
係数比較して、 2A=4 、 2B−3A=0
これを解いて、A=2 、B=3 より、特殊解は、2X+3 となる。
(注意) さらに、一般解を求めるには、特性方程式の解が、1
と 2 なので、
微分方程式 Y”−3Y’+2Y=0 の一般解は、定理Aより、
a
ex+b
e2x (但し、a、b は定数)
したがって、微分方程式 Y”−3Y’+2Y=4X の一般解は、定理Bより、
a
ex+b
e2x+2X+3 (但し、a、b は定数)
となる。
(別解) 微分演算子Dに関する公式を用いると、次のように鮮やかに特殊解が求めら
れる。
(D
2−3D+2)Y=4X より、
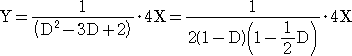
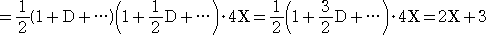
(例題2) 微分方程式 Y”−3Y’+2Y=
e3x の特殊解を求めよ。
(解) F(D)=D
2−3D+2 において、F(3)=2≠0 なので、特殊解は、(1/2)
e3x
(例題3) 微分方程式 Y”−3Y’+2Y=
Xex の特殊解を求めよ。
(解) F(D)=D
2−3D+2 において、F(D+1)=D(D−1)
よって、

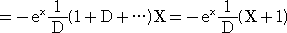

微分方程式の計算で、次の公式がよく使われる。
○重ね合わせの原理
LY=P の解を、Y
1 、LY=Q の解を、Y
2 とするとき、Y
1+Y
2 は、LY=P+Q
の解となる。
この重ね合わせの原理から、 LY=P の一般解を求めるには、その一つの特殊解
に、LY=0 の一般解を加えればよいことになる。
○定数変化法
LY=0 の2つの特殊解 Y
1と Y
2 が分かっている場合、Y=βY
1+γY
2 において
β、γを X の関数として、 LY=P に代入し、一般解を求める方法のことをいう。
○階数低下法(ダランベール)
LY=0 の1つの特殊解 Y
1 が分かっている場合
、 Y=uY
1 として、LY=P に代入
して、u’に関する1階の線形微分方程式をつくる方法のことをいう。
1階線形の場合、求積法でその一般解を求めることができる。
(参考文献: 柴岡泰光 著 線形空間 (裳華房))
(追記) 平成21年7月5日付け
当HPがいつもお世話になっているS(H)さんから次の問題が紹介された。
例題 微分方程式 Y”+Y=secX を定数変化法により解け。
(解) Y”+Y=0 の2つの特殊解 Y
1、 Y
2 を、Y
1=cos X 、Y
2=sin X とする。
これらについて、 Y
1”+Y
1=0 、 Y
2”+Y
2=0 が成り立つことは明らかだろう。
そこで、 Y=a・cos X+b・sin X ( a、b は、X の関数) とおく。
このとき、この解が、微分方程式 Y”+Y=secX の特殊解になるように、a、b
を定
めればよい。 Y=a・cos X+b・sin X の両辺を微分して、
Y’=a’・cos X−a・sin X+b’・sin X+b・cos
X
=(a’・cos X+b’・sin X)+(−a・sin
X+b・cos X)
特殊解を求めるために、
a’・cos X+b’・sin X=0 と考える。
このとき、 Y’=−a・sin X+b・cos X となる。
さらに、両辺を微分して、
Y”=−a’・sin X−a・cos X+b’・cos X−b・sin
X
=(−a’・sin X+b’・cos X)+(−a・cos
X−b・sin X)
=(−a’・sin X+b’・cos X)−Y
Y”+Y=secX が成り立つためには、
−a’・sin X+b’・cos X=secX
が成り立てばよい。
よって、
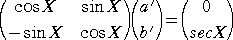
(左辺の係数行列の行列式は、 Y
1、 Y
2 のWronskianとなる!)
これを解いて、 a’=−tan X 、 b’=1 より、 a=log|cos
X| 、 b=X から、
Y=log|cos X|・cos X+X・sin X
が、Y”+Y=secX の特殊解となる。
よって、重ね合わせの原理により、微分方程式 Y”+Y=secX の一般解は、
Y=(a+log|cos X|)・cos X+(b+X)・sin
X
となる。(終)