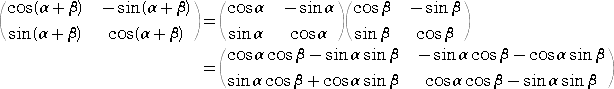壛朄掕棟丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂娭悢 俥乮倶亄倷乯 傪丄 俥乮倶乯丄 俥乮倷乯 偱昞偡掕棟偼丄壛朄掕棟偲尵傢傟傞丅妋棪偺壛朄掕棟
傕崅峑偱偺妛廗帠崁偩偑丄嶰妏娭悢偺壛朄掕棟偑嵟傕塭嬁椡偑戝偒偄丅
丂嶰妏娭悢偺壛朄掕棟
丂兛丄兝 傪擟堄偺妏偲偟偰丄師偺摍幃偑惉傝棫偮丅
乮侾乯丂倱倝値乮兛亄兝乯亖倱倝値兛們倧倱兝亄們倧倱兛倱倝値兝
乮俀乯丂倱倝値乮兛亅兝乯亖倱倝値兛們倧倱兝亅們倧倱兛倱倝値兝
乮俁乯丂們倧倱乮兛亄兝乯亖們倧倱兛們倧倱兝亅倱倝値兛倱倝値兝
乮係乯丂們倧倱乮兛亅兝乯亖們倧倱兛們倧倱兝亄倱倝値兛倱倝値兝
乮俆乯丂倲倎値乮兛亄兝乯亖乮倲倎値兛亄倲倎値兝乯/乮侾亅倲倎値兛倲倎値兝乯
乮俇乯丂倲倎値乮兛亅兝乯亖乮倲倎値兛亅倲倎値兝乯/乮侾亄倲倎値兛倲倎値兝乯
丂偙偺掕棟傪徹柧偡傞曽朄偼偄傠偄傠抦傜傟偰偄傞丅
丂堦斒揑側応崌傪徹柧偡傞偵偼丄乽堦師曄姺偺峫偊乿傗乽梋尫掕棟乿傪棙梡偟偰帵偝傟傞偑丄
庤偭庢傝憗偔塻妏偺斖埻偱擺摼偝偣傞曽朄偲偟偰偼丄乽婔壗揑側曽朄乿傗乽嶰妏宍偺柺愊乿傪
棙梡偡傞傕偺偑桳柤偩傠偆丅
丂偙偺儁乕僕偱偼丄偙傟傜偺徹柧曽朄傪傑偲傔丄偝傜偵丄偙傟傜偲偼傂偲枴傕傆偨枴傕堘偆巃
怴側徹柧曽朄偵偮偄偰尋媶偟傛偆偲巚偆丅
丂壛朄掕棟傪偁傑傝摢傪巊傢偢庤偭庢傝憗偔徯夘偟偨偄偺偱丄巹偼丄偄偮傕柺愊傪梡偄偨徹
柧乮棯徹丠乯傪嵦梡偟偰偄傞丅偨偩丄堦斒揑偱偼側偄偺偑怱巆傝偩偑丄弶怱幰傪擺摼偝偣偰
偲傝偁偊偢偼壛朄掕棟傪巊偄偙側偟偰傕傜偆偺偵偼廫暘偩丅
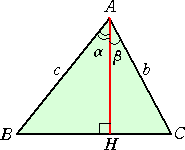 |
丂丂丂嵍恾偵偍偄偰丄丂俛俫亖們丒倱倝値兛丂丄丂俠俫亖倐丒倱倝値兝丂偱丄
丂丂俙俫亖們丒們倧倱兛亖倐丒們倧倱兝丂偱偁傞丅偙偺偲偒丄
丂丂丂丂仮俙俛俠亖乮1/2乯倐們丒倱倝値乮兛亄兝乯
丂丂丂丂仮ABH亄仮俙俠俫
丂丂丂亖乮1/2乯們丒倱倝値兛丒倐丒們倧倱兝亄乮1/2乯倐丒倱倝値兝丒們丒們倧倱兛
|
丂仮俙俛俠亖仮ABH亄仮俙俠俫丂側偺偱丄
丂丂乮1/2乯倐們丒倱倝値乮兛亄兝乯亖乮1/2乯們丒倱倝値兛丒倐丒們倧倱兝亄乮1/2乯倐丒倱倝値兝丒們丒們倧倱兛
偡側傢偪丄丂丂倱倝値乮兛亄兝乯亖倱倝値兛丒們倧倱兝亄們倧倱兛丒倱倝値兝丂丂偑惉傝棫偮丅
丂偙偺徹柧偲摨掱搙偺棯徹偲偟偰丄恾宍傪棙梡偡傞曽朄傕抦傜傟偰偄傞丅
乮徹柧偵棙梡偡傞恾偑偲偰傕媄岻揑偱丄傛偔愄偺嫵壢彂偵嵹偭偰偄偨偑巹帺恎偁傑傝岲偒側曽朄偱偼
側偄丏丏丏偲偢偭偲巚偭偰偒偨偑丄嵟嬤傛偆傗偔偦偺徹柧偺枴傢偄偑棟夝偱偒傞傛偆偵側偭偨両乯
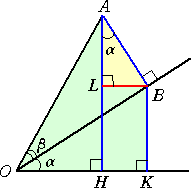 |
丂嵍恾偵偍偄偰丄丂俷俙亖侾丂偲偡傞丅丂偙偺偲偒丄
丂丂丂俴俫亖俛俲亖們倧倱兝丒倱倝値兛丂側偺偱丄
丂丂丂俙俫亖俙俴亄俴俫亖倱倝値兝丒們倧倱兛亄們倧倱兝丒倱倝値兛
丂丂傑偨丄丂俙俫亖倱倝値乮兛亄兝乯丂偱傕偁傞偺偱丄
丂丂丂倱倝値乮兛亄兝乯亖倱倝値兛丒們倧倱兝亄們倧倱兛丒倱倝値兝 |
丂摨條偵偟偰丄丂俷俲亖們倧倱兝丒們倧倱兛丂丄丂俫俲亖俛俴亖倱倝値兝丒倱倝値兛丂側偺偱丄
丂丂俷俫亖們倧倱乮兛亄兝乯亖俷俲亅俫俲亖們倧倱兝丒們倧倱兛亅倱倝値兝丒倱倝値兛
丂偡側傢偪丄丂丂們倧倱乮兛亄兝乯亖們倧倱兛丒們倧倱兝亅倱倝値兛丒倱倝値兝丂丂偑惉傝棫偮丅
乮僐儊儞僩乯丂恾宍傪棙梡偡傞偲丄倱倝値乮兛亄兝乯丄們倧倱乮兛亄兝乯偑堦婥偵愢柧偱偒傞偲偄偆棙揰
丂丂丂丂丂丂偑偁傞丅
丂偙傟傜偺壛朄掕棟偺妎偊曽偲偟偰偼丄師偺傛偆側傕偺偑抦傜傟偰偄傞丅
丂倱倝値乮兛亄兝乯 亖 倱倝値兛丒們倧倱兝丂亄丂們倧倱兛丒倱倝値兝
丂丂丂丂嶇偄偨偼丄丂嶇偄偨航咏丄 航咏嶇偄偨
丂們倧倱乮兛亄兝乯 亖 們倧倱兛丒們倧倱兝丂丂亅丂丂倱倝値兛丒倱倝値兝
丂丂丂丂僐僗儌僗偼丄丂航咏丄航咏丂偍乣丂嶇偄偨丄嶇偄偨
丂偙偺妎偊曽傪崱偺庒幰偵帵偟偰傕丄偁傑傝斀墳偑曉偭偰偙側偄丅乮椻傔偰偄傞偺偐丄抪偢
偐偟偄偺偐丄曫傟偰偄傞偺偐丏丏丏偳偭偪偐側丠乯埲慜偼丄偙偺妎偊曽傪徯夘偡傞偲丄偟偽傜
偔偼悢妛埲奜偺帪娫偱傕乽僐僗儌僗嶇偄偨丄丒丒丒丅僐僗儌僗丄僐僗儌僗丄丒丒丒丅乿偲丄曈傝峔傢偢
暦偙偊偨傕偺偩偑丏丏丏丅
丂巹偑崅峑惗偺崰丄偙偺壛朄掕棟傪丄偳偺傛偆偵偟偰妎偊偨偐丄幚偼丄偁傑傝婰壇偑掕偐
偱偼側偄丅忋婰偱弎傋偨乽嶇偄偨僐僗儌僗丄丒丒丒乿偱側偄偙偲偩偗偼妋偐偩偑丏丏丏丅傕偟偐
偟偰壗偺堘榓姶傕側偔庴偗擖傟傜傟偨偺偐傕丏丏丏丠
丂忋婰偺徹柧偱偼丄兛 丄兝 偑塻妏偱丄兛亄兝 傕侾俉侽搙傑偨偼俋侽搙偺斖埻撪偲偄偆偙偲偱丄尩
偟偔捛媶偡傟偽丄偲偰傕徹柧偲嫻傪偼偭偰尵偊傞戙暔偱偼側偄丅
丂兛丄兝 傪擟堄偺妏偲偟偰丄堦斒揑偵徹柧偡傞曽朄偲偟偰偼丄乽堦師曄姺乿傪棙梡偡傞曽朄偑
傛偔抦傜傟偰偄傞丅
丂尨揰拞怱偺妏兤傪昞偡堦師曄姺偼丄
丂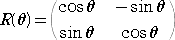
偱昞偝傟傞丅偙偺峴楍偼丄暋慺悢偺悽奅偱偼丄丂們倧倱兤亄倝丒倱倝値兤丂偵憡摉偡傞丅
丂尨揰拞怱偵丄妏 兝 偩偗夞揮偟偨屻丄偝傜偵丄妏 兛 偩偗夞揮偝偣傞偙偲偼丄尨揰拞怱偵丄妏
兛亄兝 偩偗夞揮偝偣傞偙偲偵摍偟偄偺偱丄師偺摍幃偑惉傝棫偮丅
丂丂俼乮 兛 亄 兝 乯 亖 俼乮 兛 乯丒 俼乮 兝 乯
偟偨偑偭偰丄
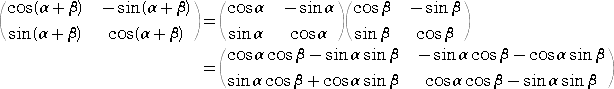
忋幃偐傜丄倱倝値乮兛亄兝乯亖倱倝値兛丒們倧倱兝亄們倧倱兛丒倱倝値兝
丂丂們倧倱乮兛亄兝乯亖們倧倱兛丒們倧倱兝亅倱倝値兛丒倱倝値兝
偑惉傝棫偮偙偲偼帺柧偩傠偆丅
乮僐儊儞僩乯丂忋婰偺徹柧偼懡偔偺嫵壢彂偱嵦梡偝傟偰偄傞傕偺偩偑壗偲側偔弞娐榑朄偱偼丠
丂丂丂丂丂丂偲偄偆塡傕偁傝拲堄偑昁梫偱偁傞丅
丂傗偼傝梋尫掕棟傪棙梡偡傞徹柧偑堦斣怣棅偝傟傞曽朄偩傠偆偐丠
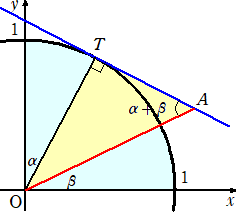
丂兛丄兝 傪擟堄偺妏偲偡傞丅揰 俤乮 侾 丆 侽 乯傪尨揰拞怱偵妏 兛 偩偗夞揮偟丄憡帡斾
倎 偺憡帡
奼戝偱摼傜傟傞揰傪 俙 偲偟丄摨條偵丄揰 俤乮 侾 丆 侽 乯傪尨揰拞怱偵妏 兝
偩偗夞揮偟丄憡帡
斾 倐 偺憡帡奼戝偱摼傜傟傞揰傪 俛 偲偡傞丅
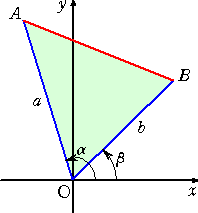 |
丂丂偙偺偲偒丄俙乮 倎們倧倱兛 丆 倎倱倝値兛 乯 丄俛乮 倐們倧倱兝 丆 倐倱倝値兝
乯
丂側偺偱丄俀揰俙俛娫偺嫍棧偺暯曽偼丄
丂丂丂丂乮倎們倧倱兛亅倐們倧倱兝乯2亄乮倎倱倝値兛亅倐倱倝値兝乯2
丂丂丂亖倎2亄倐2亅俀倎倐乮們倧倱兛丒們倧倱兝亄倱倝値兛丒倱倝値兝乯
丂侽 乣 兾 偺斖埻偱丄佢俙俷俛偺戝偒偝偼丄値 傪惍悢偲偟偰
丂丂丂丂丂兛亅兝 亇 俀値兾丂乮傑偨偼丄丂兝亅兛 亇 俀値兾丂乯
丂偲昞偝傟傞丅 |
丂壗傟偵偟偰傕丄仮俷俙俛偵偍偄偰丄梋尫掕棟偵傛傝丄丂俙俛2亖倎2亄倐2亅俀倎倐們倧倱乮兛亅兝乯
丂偟偨偑偭偰丄丂們倧倱乮兛亅兝乯亖們倧倱兛丒們倧倱兝亄倱倝値兛丒倱倝値兝丂丂偑惉傝棫偮丅
丂忋幃偺 兝 偵丄亅兝 傪戙擖偡傟偽丄丂們倧倱乮兛亄兝乯亖們倧倱兛丒們倧倱兝亅倱倝値兛丒倱倝値兝
傑偨丄 兛 偵丄兾/俀亅兛丂傪戙擖偡傟偽丄丂
丂丂們倧倱乮兾/俀亅兛亅兝乯亖們倧倱乮兾/俀亅兛乯丒們倧倱兝亄倱倝値乮兾/俀亅兛乯丒倱倝値兝
偡側傢偪丄倱倝値乮兛亄兝乯亖倱倝値兛丒們倧倱兝亄們倧倱兛丒倱倝値兝
丂偙偺幃偺 兝 偵丄亅兝 傪戙擖偡傟偽丄丂丂倱倝値乮兛亅兝乯亖倱倝値兛丒們倧倱兝亅們倧倱兛丒倱倝値兝
偑摼傜傟傞丅
丂傑偨丄忋恾偱 倎亖倐亖侾 偲偟偰丄仮俷俙俛偺柺愊偺寁嶼偐傜傕壛朄掕棟偼帵偝傟傞丅
丂丂俙乮 們倧倱兛 丆 倱倝値兛 乯 丄俛乮 們倧倱兝 丆 倱倝値兝 乯丂傛傝丄
丂仮俷俙俛亖乮侾/俀乯乥們倧倱兛倱倝値兝亅倱倝値兛們倧倱兝乥
丂丂偙偙偱丄丂兾/俀亙兛亙兾丂丄丂侽亙兝亙兾/俀丂偲偡傞偲丄
丂仮俷俙俛亖乮侾/俀乯乮倱倝値兛們倧倱兝亅們倧倱兛倱倝値兝乯
丂堦曽丄仮俷俙俛亖乮侾/俀乯倱倝値乮兛亅兝乯丂側偺偱丄倱倝値乮兛亅兝乯亖倱倝値兛們倧倱兝亅們倧倱兛倱倝値兝
偑惉傝棫偮丅偙偺幃傪梡偄傟偽丄懠偺壛朄掕棟傕摫偐傟傞丅
丂嵟嬤丄偙偺嶰妏娭悢偺壛朄掕棟偵娭偟偰師偺傛偆側巃怴側徹柧偵愙偡傞婡夛偑偁偭偨丅
丂俀奒慄宍旝暘曽掱幃偺夝傪棙梡偡傞曽朄偱偁傞丅
丂旝暘曽掱幃丂倷乭亄倷亖侽丂偺堦斒夝偼丄倷亖俙倱倝値倶亄俛們倧倱倶丂乮俙丄俛偼掕悢乯
偱梌偊傜傟傞丅乮仺嶲峫丗乽慄宍旝暘曽掱幃偵偍偗傞忢幆揑庤抜乿乯
丂偦偙偱丄丂俥乮倶乯亖倱倝値乮倶亄倷乯丂偲偍偔偲丄俥乮倶乯偼丄旝暘曽掱幃丂倷乭亄倷亖侽丂偺夝側偺偱丄
丂倱倝値乮倶亄倷乯亖俙倱倝値 倶亄俛們倧倱 倶丂乮俙丄俛偼掕悢乯
偲彂偗傞丅忋幃偱丄倶亖侽丂偲偍偔偲丄丂倱倝値 倷亖俛丂偱丄倶亖兾/俀丂偲偍偔偲丄
丂倱倝値乮兾/俀亄倷乯亖俙倱倝値 兾/俀亄俛們倧倱 兾/俀丂丂偡側傢偪丄丂們倧倱
倷亖俙
丂傛偭偰丄丂倱倝値乮倶亄倷乯亖倱倝値 倶丒們倧倱 倷亄們倧倱 倶丒倱倝値 倷
摨條偵丄丂俧乮倶乯亖們倧倱乮倶亄倷乯丂偲偍偔偲丄俧乮倶乯偼丄旝暘曽掱幃丂倷乭亄倷亖侽丂偺夝側偺偱丄
丂們倧倱乮倶亄倷乯亖俠倱倝値 倶亄俢們倧倱 倶丂乮俠丄俢偼掕悢乯
偲彂偗傞丅忋幃偱丄倶亖侽丂偲偍偔偲丄丂們倧倱 倷亖俢丂偱丄倶亖兾/俀丂偲偍偔偲丄
丂們倧倱乮兾/俀亄倷乯亖俠倱倝値 兾/俀亄俢們倧倱 兾/俀丂丂偡側傢偪丄丂亅倱倝値
倷亖俠
丂傛偭偰丄丂們倧倱乮倶亄倷乯亖們倧倱 倶丒們倧倱 倷亅倱倝値 倶丒倱倝値 倷
乮僐儊儞僩乯丂嶰妏娭悢偺旝暘偺徹柧偵丄壛朄掕棟偑巊傢傟傞偺偱丄弞娐榑朄偵側傞傛偆側
丂丂丂丂丂丂丏丏丏梊姶丅偱傕丄岞幃偺摫偒曽偲偟偰偼丄偲偰傕僄儗僈儞僩偵姶偠傞丅
乮捛婰乯丂暯惉俀侽擭俆寧俋擔晅偗
丂忋婰偱丄旝暘曽掱幃丂倷乭亄倷亖侽丂偺堦斒夝偼丄丂倷亖俙倱倝値倶亄俛們倧倱倶丂乮俙丄俛偼掕悢乯
偱梌偊傜傟傞偙偲傪梡偄偨丅
丂捠忢丄偙偺徹柧偼忋婰偺嶲峫儁乕僕偵偁傞傛偆偵側偝傟傞偑丄師偺傛偆側慛傗偐側徹柧
傕抦傜傟偰偄傞丅偙偺徹柧傪嵟弶偵尒偄偩偟偨曽偵宧暈偡傞偽偐傝偱偁傞丅
丂傑偢丄丂倷亖俥乮倶乯 傪丄旝暘曽掱幃丂倷乭亄倷亖侽丂偺夝偲偡傞偲丄丂俥乮倶乯2亄俥乫乮倶乯2丂偼掕
悢娭悢偵側傞偲偄偆惈幙偵拲栚偟側偗傟偽側傜側偄丅
乮偙偺帠幚偼丄愊暘場巕傪梡偄偨夝朄偵廃抦偟偰偄傟偽丄傎偲傫偳帺柧偩傠偆両乯
丂幚嵺偵丄丂倄亖俥乮倶乯2亄俥乫乮倶乯2丂偲偍偔偲丄
丂倄乫亖俀俥乮倶乯俥乫乮倶乯亄俀俥乫乮倶乯俥乭乮倶乯亖俀俥乫乮倶乯乮俥乭乮倶乯亄俥乮倶乯乯亖侽
丂傛偭偰丄丂倄亖俥乮倶乯2亄俥乫乮倶乯2丂偼掕悢娭悢偲側傞丅
丂偙偺帠幚傪梡偄傞偲丄師偺傛偆側暿徹偑摼傜傟傞丅
乮暿徹乯丂倷亖俥乮倶乯
傪丄旝暘曽掱幃丂倷乭亄倷亖侽丂偺夝偲偡傞丅
丂偄傑丄幚悢抣娭悢丂俧乮倶乯亖俥乮倶乯亅俥乫乮侽乯倱倝値 倶 亅俥乮侽乯們倧倱倶丂傪掕傔傞丅
丂偙偺偲偒丄丂俧乫乮倶乯亖俥乫乮倶乯亅俥乫乮侽乯們倧倱 倶 亄俥乮侽乯倱倝値倶
丂丂俧乭乮倶乯亖俥乭乮倶乯亄俥乫乮侽乯倱倝値 倶 亄俥乮侽乯們倧倱倶
側偺偱丄丂俧乭乮倶乯亄俧乮倶乯亖俥乭乮倶乯亄俥乮倶乯亖侽
丂傛偭偰丄丂俧乮倶乯偼丄旝暘曽掱幃丂倷乭亄倷亖侽丂偺夝偲側傞丅
丂偙偺偲偒丄丂俧乮倶乯2亄俧乫乮倶乯2丂偼掕悢娭悢偲側傞丅
丂偙偙偱丄丂俧乮侽乯亖俥乮侽乯亅俥乮侽乯亖侽丂丄丂俧乫乮侽乯亖俥乫乮侽乯亅俥乫乮侽乯亖侽丂側偺偱丄
丂俧乮倶乯2亄俧乫乮倶乯2亖侽丂偑惉傝棫偮丅
丂俧乮倶乯丄俧乫乮倶乯偼幚悢抣娭悢側偺偱丄丂俧乮倶乯亖侽丂偐偮丂俧乫乮倶乯亖侽
丂傛偭偰丄丂俥乮倶乯亅俥乫乮侽乯倱倝値 倶 亅俥乮侽乯們倧倱 倶 亖侽丂傛傝丄
丂俥乮倶乯亖俥乫乮侽乯倱倝値 倶 亄俥乮侽乯們倧倱 倶丂偑惉傝棫偮丅偡側傢偪丄
丂俥乫乮侽乯亖俙丂丄俥乮侽乯亖俛丂偲偍偔偲丄俥乮倶乯亖俙倱倝値 倶 亄俛們倧倱 倶丂偲彂偗傞丅乮徹廔乯
乮僐儊儞僩乯丂偙偺暿徹偩偲丄愊暘寁嶼傪偟側偔偰傕旝暘曽掱幃偑夝偗偨傢偗偱丄偲偭偰傕妝偱
丂丂丂丂丂丂偡偹両
乮捛婰乯丂暯惉俀俀擭俋寧俀俉擔晅偗
丂摉俫俹偺乽惓尫掕棟偲梋尫掕棟乿偺儁乕僕傪惍棟偟偰偄傞拞偱丄惓尫掕棟偲戞堦梋尫掕棟
傪梡偄傞偲丄壛朄掕棟偑帵偝傟傞偙偲偵婥偯偐偝傟偨丅
 |
丂丂丂嵍恾偵偍偄偰丄戞堦梋尫掕棟偑惉傝棫偮丅
丂丂
丂丂
丂丂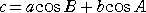 |
丂傑偨丄惓尫掕棟
丂丂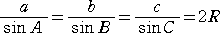 丂乮偨偩偟丄俼 偼仮俙俛俠 偺奜愙墌偺敿宎乯
丂乮偨偩偟丄俼 偼仮俙俛俠 偺奜愙墌偺敿宎乯
傛傝丄丂倎亖俀俼倱倝値俙丂丄倐亖俀俼倱倝値俛丂丄們亖俀俼倱倝値俠丂偑惉傝棫偮丅
丂偙傟傜傪丄丂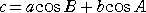 丂偵戙擖偡傞偲丄
丂偵戙擖偡傞偲丄
丂俀俼倱倝値俠亖俀俼倱倝値俙們倧倱俛亄俀俼倱倝値俛們倧倱俙
偡側傢偪丄丂倱倝値俠亖倱倝値俙們倧倱俛亄們倧倱俙倱倝値俛丂偑惉傝棫偮丅
丂偙偙偱丄丂倱倝値俠亖倱倝値乮兾亅俙亅俛乯亖倱倝値乮俙亄俛乯丂側偺偱丄
丂倱倝値乮俙亄俛乯亖倱倝値俙們倧倱俛亄們倧倱俙倱倝値俛
偑惉傝棫偮丅偙傟偼丄惓尫偺壛朄掕棟偱偁傞丅偙偺偲偒丄忋幃偵偮偄偰丄
丂俛偵亅俛傪戙擖偡傞偙偲偵傛傝丄丂倱倝値乮俙亅俛乯亖倱倝値俙們倧倱俛亅們倧倱俙倱倝値俛
丂俙偵兾/俀亅俙傪戙擖偡傟偽丄丂們倧倱乮俙亅俛乯亖們倧倱俙們倧倱俛亄倱倝値俙倱倝値俛
丂丂偝傜偵丄俛偵亅俛傪戙擖偡傞偙偲偵傛傝丄丂們倧倱乮俙亄俛乯亖們倧倱俙們倧倱俛亅倱倝値俙倱倝値俛
偑摼傜傟傞偙偲偼丄捠忢嫵壢彂摍偱弎傋傜傟傞偙偲偲摨條偱偁傞丅
乮僐儊儞僩乯丂偙偺庤朄偺庛揰偼丄妏俙丄俛丄俠偑嶰妏宍偺撪妏偲偄偆惂尷偑晅偄偰偄傞偙偲偩
丂丂丂丂丂丂傠偆丅偨偩丄恖傪愢摼偡傞偵偼廫暘偩傠偆偑丄倱倝値乮兾亅俙亅俛乯亖倱倝値乮俙亄俛乯偲偄
丂丂丂丂丂丂偆岞幃偑庒姳晘嫃偑崅偄偐傕抦傟側偄丅
乮捛婰乯丂暯惉俀俇擭係寧俀俈擔晅偗
丂忋婰偱弎傋偨傛偆偵丄尨揰拞怱偺妏兤傪昞偡堦師曄姺
丂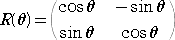
偼丄暋慺悢偺悽奅偱偼丄丂們倧倱兤亄倝丒倱倝値兤丂偵憡摉偡傞丅偟偐傕丄摍幃
丂俼乮 兛 亄 兝 乯 亖 俼乮 兛 乯丒 俼乮 兝 乯
偐傜丄兛亖兝偲偟偰丄丂俼乮 兛 乯2亖俼乮 俀兛 乯丂偑惉傝棫偮丅堦斒偵丄
丂俼乮 兛 乯値亖俼乮 値兛 乯
丂偙傟偼丄暋慺悢偺悽奅偱丄丂乮們倧倱兤亄倝丒倱倝値兤乯値亖們倧倱(値兤)亄倝丒倱倝値(値兤)丂傪堄枴偟丄
僪丒儌傾僽儖偺掕棟偲偟偰抦傜傟傞丅
丂摉俫俹撉幰偺俫俶乽CEGIPO乿偝傫偐傜丄僪丒儌傾僽儖偺掕棟傪梡偄偨嶰妏娭悢偺値攞妏偺岞
幃偺忋庤偄昞尰曽朄偵偮偄偰偛嫵帵捀偄偨丅乮暯惉俀俇擭係寧俀俇擔晅偗乯
丂忋幃偱丄値偵亅値傪戙擖偟偰丄丂乮們倧倱兤亄倝丒倱倝値兤乯-値亖們倧倱(亅値兤)亄倝丒倱倝値(亅値兤)
傛傝丄
丂丂丂丂cos(n兤)亅i丒sin(n兤)亖(cos兤亅i丒sin兤)値丂丒丒丒丂(*)
丂傑偨丄丂cos(n兤)亄i丒sin(n兤)亖(cos兤亄i丒sin兤)値丂丒丒丒丂(**)丂偲偡傞丅
丂偙偺偲偒丄(*)丄(**)傪曈乆壛偊偰丄椉曈傪俀偱妱傞偲丄
丂丂cos(n兤)亖{(cos兤亄i丒sin兤)値亄(cos兤亅i丒sin兤)値}/俀丂丒丒丒(#)
丂摨條偵丄(*)丄(**)傪曈乆堷偄偰丄椉曈傪俀偱妱傞偲丄
丂丂i丒sin(n兤)亖{(cos兤亄i丒sin兤)値亅(cos兤亅i丒sin兤)値}/俀
丂偡側傢偪丄丂sin(n兤)亖亅i丒{(cos兤亄i丒sin兤)値亅(cos兤亅i丒sin兤)値}/俀丂丒丒丒(##)
丂偝傜偵丄cos兤亗0偺帪偼丄(##)/(#)傛傝丄
丂tan(n兤)亖亅i丒{(cos兤亄i丒sin兤)値亅(cos兤亅i丒sin兤)値}/{(cos兤亄i丒sin兤)値亄(cos兤亅i丒sin兤)値}
丂丂丂丂丂丂亖亅倝丒{(侾亄i丒tan兤)n亅(侾亅i丒tan兤)n}/{(侾亄i丒tan兤)n亄(侾亅i丒tan兤)n}丂丒丒丒(###)
偲側傝傑偡丅(^_^)v
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭係寧俀俇擔晅偗乯
丂(*)偼丄(**)偺兤偵-兤傪戙擖偟偰傕摼傜傟傑偡偹丅
乮捛婰乯丂壛朄掕棟偺徹柧偵偮偄偰丄俫俶乽憪栞乿偝傫偐傜偺搳峞偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俈擭侾侽寧俀侾擔晅偗乯
丂杮斣偺庴尡偱偼丄乽岞幃傪徹柧偣傛乿偲偄偆栤戣偑懡偔尒傜傟傞偲偄偆榖傪傛偔暦偒傑偡丅
(2013擭戝嶃戝妛慜婰側偳)傑偨丄1999擭搶嫗戝妛慜婜偺栤戣偱偼丄壛朄掕棟傪徹柧偝偣
傞栤戣偑弌戣偝傟傑偟偨丅
丂偙偺栤戣偵偮偄偰丄嫵壢彂偵嵹偭偰偄傞傛偆側壛朄掕棟偺徹柧偱偼側偔丄暿夝偑峫偊傜傟
側偄偐偲偄偆偙偲偱丄暋慺悢傪梡偄傞曽朄偱峫偊偰傒傑偟偨丅埲壓偵偦偺奣棯傪帵偟傑偡丅
丂揰A(cos兛丆sin兛)傪兝偩偗夞揮偝偣偨揰傪B偲偡傟偽丄B偺嵗昗偼丄
(cos(兛+兝)丆sin(兛+兝))偲側傞丅乧(1)
丂埲壓丄暋慺悢暯柺忋偱峫偊傞丅揰A偺嬌宍幃 cos兛+i丒sin兛 偵傛傝丄夞揮屻偺揰B偺嬌宍
幃偼丄(cos兛+i丒sin兛)(cos兝+i丒sin兝)丂偵傛偭偰昞偝傟丄揥奐偡傞偙偲偱丄B偺嵗昗偼丄
丂(cos兛cos兝-sin兛sin兝丆sin兛cos兝+cos兛sin兝)
偲媮傑傞丅偙傟偼丄(1)偲憡摍偟偄偐傜壛朄掕棟偑摫偗傞丅
丂媈栤揰偲偟偰丄暋慺悢偺夞揮堏摦偵偮偄偰丄偁傞暋慺悢傪 倸 偲偟偨嵺偵丄倸 傪尨揰拞怱偵
兛偩偗夞揮偟丄暋慺悢w偵堏偡偙偲傪丄倵亖倸(cos兛+i丒sin兛)偲彂偄偰偄傑偡偑丄偙傟偼丄柍忦
審偵巊梡偟偰傛偄傕偺側偺偱偟傚偆偐丅
丂杮栤偱偼丄壛朄掕棟傪徹柧偡傞栤戣偱偡偐傜丄暋慺悢偺夞揮偺張棟帺懱偵壛朄掕棟偑棈
傫偱偄傞偺偱偁傟偽丄偙偺徹柧偼弞娐榑朄偵娮偭偰偟傑偄傑偡丅
壛朄掕棟偑棈傫偱偄偨偲偟偰傕丄偦傟傪夞旔偱偒傞曽朄偑偁傟偽傛偄偺偱偡偑丒丒丒
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俈擭侾侽寧俀侾擔晅偗乯
丂戝妛庴尡偱偼丄彫妛峑偐傜崅峑傑偱偺嫵壢彂偵愢柧側偄偟徹柧偑偁傞傕偺偼偦傟偵弨偠
傞偼偢偱偡丅偱偡偐傜丄悢妛III偺嫵壢彂偵暋慺悢偺夞揮傪壛朄掕棟傪梡偄偰愢柧偟偰偁傟
偽乮偁傞偄偼壛朄掕棟傪梡偄偰愢柧偟偨傕偺傪梡偄偰愢柧偟偰偁傟偽乯傾僂僩偱偡丅
丂崱丄庤尦偵悢妛III偺嫵壢彂偑側偄偺偱抐尵偼偱偒傑偣傫偑丄偨偟偐暋慺悢偺愊偱曃妏偑
榓偵側傞偙偲乮壛朄掕棟傪梡偄偰偄傞乯偱丄嶰妏宍偺崌摨乮偲偄偆偐奼戝弅彫娷傔偰憡帡乯傪
徹柧偟偰傑偣傫偱偟偨偭偗丠
丂柍榑丄暋慺悢偺愊偑夞揮偵側傞偙偲傪壛朄掕棟傪巊傢偢偵帵偡徹柧傪暪婰偡傟偽戝忎晇
偱偟傚偆偑丄媝偭偰庤娫偱偡丅
丂壛朄掕棟偑棈傓偺傪夞旔偡傞曽朄傕側偔偼側偄偲巚偄傑偡偑丄傗偭傁傝庤娫偼憹偊傞偩偗
偐偲乧乧丅
乮僐儊儞僩乯丂庤尦偵偁傞悢妛嘨偺嫵壢彂乮悢尋弌斉乯偱偼丄巜摫偺棳傟偼師偺傛偆偵側偭偰偄
丂丂丂丂丂丂傞傛偆偱偡丅
乮侾乯丂暋慺悢偺嬌宍幃昞帵丂倸亖倎亄倐丒倝丂偐傜丂倸亖倰乮們倧倱兤亄倝丒倱倝値兤乯丂傊偺摫擖
乮俀乯丂嬌宍幃昞帵偺暋慺悢偺愊偲彜
丂丂倸亖cos兛+i丒sin兛丂丄倵亖cos兝+i丒sin兝丂偵懳偟偰丄
丂倸倵亖乮cos兛+i丒sin兛乯乮cos兝+i丒sin兝乯
丂丂丂亖cos兛cos兝-sin兛sin兝亄倝乮sin兛cos兝+cos兛sin兝乯
丂偙偙偱丄壛朄掕棟偵傛傝丄丂倸倵亖cos乮兛亄兝乯+i丒sin乮兛亄兝乯
丂偙偺偙偲偐傜丄暋慺悢 倸 偵暋慺悢 倵 傪妡偗傞偙偲偼丄乽夞揮乿偵側傞偙偲傪妛傇丅
乮俁乯丂僪丒儌傾僽儖偺掕棟
丂丂乮俀乯偱妛傫偩偙偲傪妶梡偟丄倸亖cos兛+i丒sin兛丂偺値忔偑丄曃妏兤偺値攞偵側傞偙偲傪妛傇丅
乮係乯丂暋慺悢偺値忔崻傪丄乮俁乯偺媡偺宍偱媮傔傞
丂偙偺傛偆側棳傟偱妛傫偱偄傞偺偱丄暋慺悢偺夞揮傪梡偄偰壛朄掕棟傪帵偡偺偼弞娐榑朄
偵側偭偰偟傑偄傑偡偹両
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偐傜栤戣傪偄偨偩偒傑偟偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俋擭俇寧俁侽擔晅偗乯
丂挿曽宍ABCD偺巻偑偁傞丅佢BCD傪曈DA偵愙偡傞傛偆偵愜傝丄偦偺偲偒偵偱偒偨愜傝栚偺
挿偝傪1偲偡傞丅偙偺巻傪巊偭偰丄sin(兛+兝)丄cos(兛+兝) 偺揥奐幃傪摫偗丅
乮僐儊儞僩乯丂壛朄掕棟偺暿徹柧偲偟偰柺敀偦偆偩偭偨偺偱峫偊偰傒傑偟偨丅壓偺恾偲嵘傔偭偙
丂丂丂丂丂丂偡傟偽柧傜偐偱偟傚偆丅偨偩丄兛亄俀兝亖俋侽亱側偺偑彮偟婥偑偐傝偐側丠
丂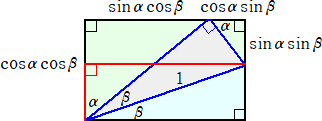
乮捛婰乯丂椷榓俀擭俁寧侾俀擔晅偗
丂忋婰偺壛朄掕棟偺徹柧偲偼堦枴傕擇枴傕堎側傞巃怴側徹柧傪嵟嬤抦傞偙偲偑偱偒偨丅
 |
丂嵍恾偺傛偆偵丄敿宎侾偺墌廃忋偵揰俿傪偲傞丅
丂俿乮倱倝値兛丆們倧倱兛乯偱偁傞丅揰俿偵偍偗傞愙慄偺曽掱幃
偼丄丂倶丒倱倝値兛亄倷丒們倧倱兛亖侾丂偱丄
丂揰俙乮俷俙們倧倱兝丆俷俙倱倝値兝乯偼愙慄忋偺揰側偺偱丄
丂丂俷俙們倧倱兝丒倱倝値兛亄俷俙倱倝値兝丒們倧倱兛亖侾
丂傛偭偰丄壛朄掕棟
丂丂倱倝値兛們倧倱兝亄們倧倱兛倱倝値兝亖侾/俷俙亖倱倝値乮兛亄兝乯
丂偑帵偝傟偨丅 |
丂傛偍偡偗偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俁寧侾俇擔晅偗乯
丂嵗昗暯柺忋偱丄揰(1丆0)丄(0丆1)傪尨揰偺傑傢傝偵兤偩偗夞揮偝偣傞偲丄嶰妏娭悢偺掕媊偲
梋妏偺岞幃丄晧妏偺岞幃傛傝
(1丆0)丂仺丂(cos兤丆sin兤)丂丄(0丆1)丂仺丂(cos(兤+兾/2)丆sin(兤+兾/2))亖(-sin兤丆cos兤)
偲堏傞丅師偵丄係揰(0丆0)丄(cos兛丆0)丄(cos兛丆sin兛)丄(0丆sin兛)傪捀揰偲偡傞挿曽宍傪尨揰
偺傑傢傝偵兝偩偗夞揮偝偣傞偲丄挿曽宍偼曄宍偟側偄偐傜丄
(cos兛丆sin兛)亖(cos兛)(1丆0)亄(sin兛)(0丆1)丂仺丂(cos兛)(cos兝丆sin兝)亄(sin兛)(-sin兝丆cos兝)
丂揰(cos兛丆sin兛)偼丄偙偺夞揮偵傛傝丄揰(cos(兛+兝)丆sin(兛+兝))偵堏偝傟傞偐傜
cos(兛+兝)=cos兛cos兝-sin兝sin兝丂丄sin(兛+兝)=sin兛cos兝+cos兛sin兝
乮弌揟尦乯丂憗堫揷悢妛僼僅乕儔儉-崅峑惗丒庴尡惗偺偨傔偺悢妛墘廗-婎杮夝朄妋擣墘廗-嶰妏娭悢
丂丂丂丂丂丂偺栤戣8(1)偺夝摎偺堦晹
乮捛婰乯丂椷榓俆擭俇寧侾侽擔晅偗
丂偙偺儁乕僕偱偼丄嶰妏娭悢偺婎杮揑側掕棟偱偁傞壛朄掕棟偺徹柧偵偮偄偰丄偄傠偄傠挷
傋偰偒偨偑丄壛朄掕棟傪尦偵丄攞妏偺岞幃丄敿妏偺岞幃丄榓愊偺岞幃丄愊榓偺岞幃傕娙扨
偵帵偝傟傞丅
乮攞妏偺岞幃乯丂倱倝値俀兤亖俀倱倝値兤們倧倱兤
丂丂們倧倱俀兤亖們倧倱2兤亅倱倝値2兤亖俀們倧倱2兤亅侾亖侾亅俀倱倝値2兤
丂丂倲倎値俀兤亖俀倲倎値兤/乮侾亅倲倎値2兤乯
丂丂倱倝値俁兤亖俁倱倝値兤亅係倱倝値3兤丂丄們倧倱俁兤亖係們倧倱3兤亅俁們倧倱兤
乮敿妏偺岞幃乯丂倱倝値2乮兤/俀乯亖乮侾亅們倧倱兤乯/俀丂丄們倧倱2乮兤/俀乯亖乮侾亄們倧倱兤乯/俀
乮榓愊偺岞幃乯丒丒丒嶰妏娭悢偵偍偗傞場悢暘夝偺岞幃偵憡摉
丂丂倱倝値俙亄倱倝値俛亖俀倱倝値乮乮俙亄俛乯/俀乯們倧倱乮乮俙亅俛乯/俀乯
丂丂倱倝値俙亅倱倝値俛亖俀們倧倱乮乮俙亄俛乯/俀乯倱倝値乮乮俙亅俛乯/俀乯
丂丂們倧倱俙亄們倧倱俛亖俀們倧倱乮乮俙亄俛乯/俀乯們倧倱乮乮俙亅俛乯/俀乯
丂丂們倧倱俙亅們倧倱俛亖亅俀倱倝値乮乮俙亄俛乯/俀乯倱倝値乮乮俙亅俛乯/俀乯
乮愊榓偺岞幃乯丒丒丒嶰妏娭悢偵偍偗傞揥奐偺岞幃偵憡摉
丂丂倱倝値兛們倧倱兝亖乮侾/俀乯乮倱倝値乮兛亄兝乯亄倱倝値乮兛亅兝乯乯
丂丂們倧倱兛倱倝値兝亖乮侾/俀乯乮倱倝値乮兛亄兝乯亅倱倝値乮兛亅兝乯乯
丂丂們倧倱兛們倧倱兝亖乮侾/俀乯乮們倧倱乮兛亄兝乯亄們倧倱乮兛亅兝乯乯
丂丂倱倝値兛倱倝値兝亖亅乮侾/俀乯乮們倧倱乮兛亄兝乯亅們倧倱乮兛亅兝乯乯
丂偙傟傜偺嬶懱揑側墳梡椺傪丄嬨廈戝妛慜婜棟宯乮俀侽侾俇乯偺栤戣傪戣嵽偵峫嶡偟偰傒傛偆丅
栤戣丂丂倱倝値2俀侽亱亄倱倝値2係侽亱亄倱倝値2俇侽亱亄倱倝値2俉侽亱亖俋/係丂傪帵偣丅
乮夝乯丂梌幃
亖乮侾亅們倧倱係侽亱乯/俀亄乮侾亅們倧倱俉侽亱乯/俀亄乮侾亅們倧倱侾俀侽亱乯/俀亄乮侾亅們倧倱侾俇侽亱乯/俀
亖俀亅乮們倧倱係侽亱亄們倧倱俉侽亱亄們倧倱侾俀侽亱亄們倧倱侾俇侽亱乯/俀
亖俋/係亅乮們倧倱係侽亱亄們倧倱俉侽亱亄們倧倱侾俇侽亱乯/俀
偙偙偱丄們倧倱係侽亱亄們倧倱俉侽亱亄們倧倱侾俇侽亱
丂丂亖俀們倧倱俇侽亱們倧倱俀侽亱亅們倧倱俀侽亱亖們倧倱俀侽亱亅們倧倱俀侽亱亖侽
側偺偱丄丂梌幃亖俋/係丂丂乮廔乯
丂師偺栤戣傕壛朄掕棟偺揔愗側墳梡椺偲側傞偩傠偆丅
栤戣丂丂倶倷 暯柺偵偍偄偰丄壓恾偺傛偆偵戜宍OABC偑偁傞丅
丂丂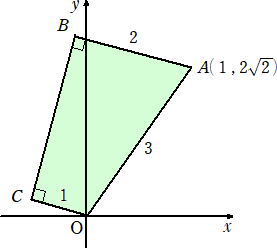
丂俙乮侾丆俀 乯偺偲偒丄俠偺嵗昗傪媮傔傛丅
乯偺偲偒丄俠偺嵗昗傪媮傔傛丅
乮夝乯丂壓恾偵偍偄偰丄尨揰俷傛傝曈俙俛偵悅慄傪壓傠偟丄偦偺懌傪俫偲偍偔丅
丂丂
丂偙偺偲偒丄俷俫亖俀 丂偱丄俫乮倶丆倷乯偲偍偔偲丄
丂偱丄俫乮倶丆倷乯偲偍偔偲丄
倶亖俀 們倧倱乮兛亄兝乯亖俀
們倧倱乮兛亄兝乯亖俀 乮們倧倱兛們倧倱兝亅倱倝値兛倱倝値兝乯
乮們倧倱兛們倧倱兝亅倱倝値兛倱倝値兝乯
丂亖俀 乮乮侾/俁乯乮俀
乮乮侾/俁乯乮俀 /俁乯亅乮俀
/俁乯亅乮俀 /俁乯乮侾/俁乯乯亖侽
/俁乯乮侾/俁乯乯亖侽
倷亖俀 倱倝値乮兛亄兝乯亖俀
倱倝値乮兛亄兝乯亖俀 乮倱倝値兛們倧倱兝亄們倧倱兛倱倝値兝乯
乮倱倝値兛們倧倱兝亄們倧倱兛倱倝値兝乯
丂亖俀 乮乮俀
乮乮俀 /俁乯乮俀
/俁乯乮俀 /俁乯亄乮侾/俁乯乮侾/俁乯乯亖俀
/俁乯亄乮侾/俁乯乮侾/俁乯乯亖俀
傛偭偰丄俷俠亖俙俫亖乮亅侾丆侽乯丂傛傝丄丂俠乮亅侾丆侽乯丂偱偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俉寧侾侽擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俈乯偺栤戣偼丄婎杮栤戣偱偁傞丅
栤戣丂丂乮侾乯丂兤傪 侽亱亙兤亙俋侽亱傪枮偨偡妏偲偟丄倱倝値兤偼俀師曽掱幃
丂丂乮倢倧倗2俁俀乯倶2亄乮倢倧倗3俋乯倶亅倢倧倗4俇係亖侽丂偺夝偱偁傞偲偡傞丅
丂丂偙偺偲偒丄們倧倱兤偺抣傪媮傔傛丅
乮俀乯丂兤傪乮侾乯偺傛偆偵掕傔傞偲偒丄們倧倱乮俀兤亄俇侽亱乯偺抣傪媮傔傛丅
乮夝乯乮侾乯丂倢倧倗2俁俀亖俆丂丄倢倧倗3俋亖俀丂丄倢倧倗4俇係亖俁丂側偺偱丄丂俆倶2亄俀倶亅俁亖侽
丂乮俆倶亅俁乯乮倶亄侾乯亖侽丂傛傝丄丂倶亖俁/俆丂丄亅侾
丂侽亱亙兤亙俋侽亱傛傝丄丂倱倝値兤亜侽丂側偺偱丄丂倱倝値兤亖俁/俆丂偙偺偲偒丄丂們倧倱兤亖係/俆
乮俀乯丂們倧倱乮俀兤亄俇侽亱乯亖乮侾/俀乯們倧倱俀兤亅乮 /俀乯倱倝値俀兤
/俀乯倱倝値俀兤
丂偙偙偱丄丂們倧倱俀兤亖們倧倱2兤亅倱倝値2兤亖侾俇/俀俆亅俋/俀俆亖俈/俀俆
丂倱倝値俀兤亖俀倱倝値兤們倧倱兤亖俀係/俀俆丂側偺偱丄
丂們倧倱乮俀兤亄俇侽亱乯亖俈/俆侽亅俀係 /俆侽亖乮俈亅俀係
/俆侽亖乮俈亅俀係 乯/俆侽丂丂乮廔乯
乯/俆侽丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧侾係擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俋乯偺栤戣偼丄婎杮栤戣偱偁傞丅
栤戣丂丂俁偮偺妏兛丄兝丄兞乮亅俋侽亱亙兛丄兝丄兞亙俋侽亱乯偑
丂倲倎値兛亄倲倎値兝亄倲倎値兞亖倲倎値兛倲倎値兝倲倎値兞
傪傒偨偡偲偒丄兛亄兝亄兞偺抣傪偡傋偰媮傔傛丅
乮夝乯丂倲倎値乮兛亄兝亄兞乯亖乮倲倎値乮兛亄兝乯亄倲倎値兞乯/乮侾亅倲倎値乮兛亄兝乯倲倎値兞乯
偙偙偱丄倲倎値乮兛亄兝乯亄倲倎値兞亖乮倲倎値兛亄倲倎値兝乯/乮侾亅倲倎値兛倲倎値兝乯亄倲倎値兞
丂丂亖乮倲倎値兛亄倲倎値兝亄倲倎値兞亅倲倎値兛倲倎値兝倲倎値兞乯亖侽丂偐傜丄
丂倲倎値乮兛亄兝亄兞乯亖侽
丂亅俀俈侽亱亙兛亄兝亄兞亙俀俈侽亱丂傛傝丄丂兛亄兝亄兞亖侽亱丄亇侾俉侽亱丂丂乮廔乯
丂丂埲壓丄岺帠拞両