(4)
数値解析法・・・解の関数値の表を、初期値から始めて次々と作っていく方法
求積法などにより、具体的に、微分方程式の解が求められなくても、実用上は、数値とし
て、その解の近似値が求まれば十分ということが多い。
このページでは、その初等的な方法を紹介する。
今、微分方程式 Y’=F(X,Y) を、初期条件 X=a のとき、Y=b のもとで解く。この
解が求積法で求めにくいとき、次の
Euler−Cauchy の解法が知られている。
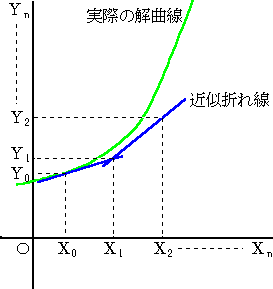
a より若干大きい値を A とし、区間[a,A]
を n 等分する。このとき、
X
0=a 、X
1、X
2、・・・X
n-1、X
n=A
さらに、
h=(A−a)/n
とおく。
点(X
0,Y
0)において、傾きF(X
0,Y
0)の
直線を引き、直線 X=X
1 との交点のY座標
を Y
1 とする。ただし、Y
0=b とする。
点(X
1,Y
1)において、傾きF(X
1,Y
1)の
直線を引き、直線 X=X
2 との交点のY座標
を Y
2 とする。
以下同様にして、左図のように、
Y
2 ,Y
3 ,・・・,Y
n を定める。
この Y
n をもって、与えられた初期条件のもとでの、微分方程式の解の X=A における
近似値とする。
以上により、その計算式をまとめれば、次のようになる。
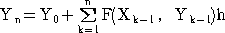
(例1) 微分方程式 Y’=X/Y (初期条件 X=0 のとき、Y=1)を考える。
この微分方程式は、求積法により解かれて、X
2−Y
2=−1 となるので、X=1 の
ときのYの値は、√2 (≒1.4142135・・・)となる。
この微分方程式に対して、実際に Euler−Cauchy の解法を適用してみよう。
手計算では大変なので、Excel のVBA を利用して求める。
Function Y(n)
X=0
Y=1
h=1/n
For i=1 To n
Y=Y+(X/Y)*h
X=X+h
Next i
End Function
Excel を起動し、[ツール]−[マクロ]−[Visual Basic Editor] とクリックして
Editor を起動し、[挿入]−[標準モジュール] を選択して、上記を記述すればよい。
後は、Excelの任意のセルに、例えば、 =Y(100) と打ち込むと、瞬時に、区間
[0 ,1]を100等分して得られた、X=1 における近似値が得られる。
計算によれば、1.4142135 の近似値を得るには、247万999等分する必
要があるようである。したがって、手計算でできる範囲(例えば、5等分、10等
分など)では、誤差が大きすぎて、使いものにならない。因みに、5等分して得ら
れる近似値は、1.4・・・が精一杯であった。
(例2) 微分方程式 Y’=Y (初期条件 X=0 のとき、Y=1)を考える。
この微分方程式は、求積法により解かれて、Y=
ex となるので、X=1 のときの
Yの値は、
e (≒2.718281・・・)となる。
この微分方程式に対して、実際に Euler−Cauchy の解法を適用してみよう。
手計算では大変なので、Excel のVBA を利用して求める。
Function Y(n)
Y=1
h=1/n
For i=1 To n
Y=Y+Y*h
Next i
End Function
Excel を起動し、[ツール]−[マクロ]−[Visual Basic Editor] とクリックして
Editor を起動し、[挿入]−[標準モジュール] を選択して、上記を記述すればよい。
後は、Excelの任意のセルに、例えば、 =Y(100) と打ち込むと、瞬時に、区間
[0 ,1]を100等分して得られた、X=1 における近似値が得られる。
計算によれば、2.718281 の近似値を得るには、123万954等分する必
要があるようである。したがって、手計算でできる範囲(例えば、5等分、10等
分など)では、誤差が大きすぎて、使いものにならない。因みに、10等分して得
られる近似値は、2.5・・・で、真の値からは程遠い。2.71828
の近似値を得
るには、少し楽になって、58万3708等分で十分のようである。
以上の2つの例からも分かるように、Euler−Cauchy の解法は基本的で分かりや
すいが、近似の程度が非常に悪い。この方法を改良したものとして、
ルンゲ・クッタ法(Runge-Kutta法)・・・積分における
シンプソンの公式のような方法
この方法をコンピュータで利用できるように改良された
ルンゲ・クッタ・ギル法
などが知られている。

