モンテカルロ法　　　　　　　　　　　　　　　　　　　　　　　

　近年コンピュータの発達により、コンピュータを用いて数学の問題を解くという時代になった。
四色問題がコンピュータの活躍により解決されたことは、四半世紀経った今でも鮮烈な記憶と
して残っている。このページでアプローチするモンテカルロ法は、解析的には解けない問題に
対して、ランダムな実験を多数回繰り返し、その結果をもとに近似的に答を求めようとする方
法である。

　定積分の計算で、被積分関数の不定積分が容易に分からないとき、近似計算により、定積
分の値を求めることになるが、次の２つの公式が知られている。

台形公式　 　　関数Ｆ(Ｘ)は、区間[ａ，ｂ] で連続とする。この区間を ｎ 等分して、 　分点を小さい方から順に、ａ＝Ｘ０，Ｘ１，Ｘ２，・・・，Ｘｎ−１，Ｘｎ＝ｂ 　とし、ＹＫ＝Ｆ(ＸＫ)、ｈ＝(ｂ−ａ)/ｎ　とする。このとき、 　 　この公式は、曲線の一部をその両端を結ぶ線分によって 置き換え、曲線の下の面積をいくつかの台形の面積の和で 近似するものである。

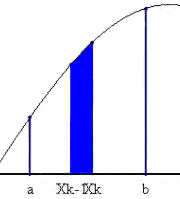シンプソン（Ｓｉｍｐｓｏｎ）の公式

　　　関数Ｆ(Ｘ)は、区間[ａ，ｂ] で連続とする。この区間を ２ｎ 等分して、分点を小さい方から

順に、ａ＝Ｘ０，Ｘ１，Ｘ２，・・・，Ｘ２ｎ−１，Ｘ２ｎ＝ｂ とし、ＹＫ＝Ｆ(ＸＫ)、ｈ＝(ｂ−ａ)/２ｎ　とする。

このとき、

　　　

　この公式は、Ｘ軸上の等間隔ｈの３点Ｘ２Ｋ−２、Ｘ２Ｋ−１、Ｘ２Ｋ をとり、これに対応する曲線上

の３点を通る放物線を考え、曲線の下の面積をいくつかの放物線の面積の和で近似するも

のである。

例

の値を、台形公式、シンプソンの公式を用いて求めてみよう。

　区間[０，１] を１０等分すると、ｈ＝０．１

このとき、Ｙ０＝１、Ｙ１＝０．９９００９９０、Ｙ２＝０．９６１５３８５

　　　　　　　　　　　Ｙ３＝０．９１７４３１２、Ｙ４＝０．８６２０６９０

　　　　　　　　　　　Ｙ５＝０．８００００００、Ｙ６＝０．７３５２９４１

　　　　　　　　　　　Ｙ７＝０．６７１１４０９、Ｙ８＝０．６０９７５６１

　　　　　　　　　　　Ｙ９＝０．５５２４８６２　　　　　　　　　　　　　　、Ｙ１０＝０．５　

従って、台形公式を用いれば、　　Ａ≒０．７８４９８１５

　　　　　シンプソンの公式を用いれば、　　Ａ≒０．７８５３９８２

因みに、正しく定積分の計算をすれば、Ａ＝π/４≒０．７８５３９８２　である。

　この定積分近似計算の第３の方法として、モンテカルロ・シミュレーションという方法がある。

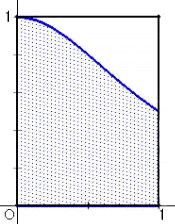上記例の関数を用いて説明することにする。 　　左図は、区間[０，１] における関数Ｆ(Ｘ)のグラフを表す。定積 　　分の値Ａを求めることは、左図の網目状の部分の面積を求め 　　ることである。今一組の乱数（α，β）を発生させ、Ｆ(α)≧β 　　となるかどうかを判定する。何組かの乱数をとり、その総数を 　　Ｎとする。このうち、上記不等式を満たすものの個数を ｒ とす 　　れば、全体の面積が１なので、比の値　ｒ/Ｎ は定積分の近似 　　値を与える。Ｎの値を十分大きくとれば、よりよい近似値となる 　　はずである。

　　乱数を発生させるには、乱数表を用いたり、乱数さいころを用いればよい。乱数さいころは、

正２０面体で、各面に０〜９の数字が２つずつ書かれ、均等に数字が出るように作られている

ものである。

　ここでは、表計算ソフトＥｘｃｅｌ のＲＡＮＤ関数を用いて乱数を発生させ、実験してみよう。

セルＡ１に　＝ＲＡＮＤ()、セルＢ１に　＝１/(１＋Ａ１＊Ａ１)、セルＣ１に　＝ＲＡＮＤ()　を入力し、

不等式を満たすかどうかの判定として、セルＤ１に　＝ＩＦ(＋Ｂ１−Ｃ１＞＝０，１，０）　を入力す

る。セルＡ１、Ｂ１、Ｃ１、Ｄ１を１〜１００００行までコピーする。

不等式を満たすものの個数計算用として、セルＥ１に　＝ＳＵＭ（Ｄ１：Ｄ１００００）　を入力する。

　１０回試行を行ったところ、次の結果を得た。

７７９０、７９４３、７８４０、７８２８、７９２５、７８７１、７８４４、７８５５、７７８７、７８３９

この標本平均は、７８５２．２ となる。

　従って、７８５２．２/１００００＝０．７８５２２　が求める定積分の近似値となる。

　上記のシミュレーションでは、１００００行までに留めたが、これをもうすこし大きくとれば、実際

値に、より近づくものと期待される。

（参考文献：木下栄蔵　著　好奇心の数学（電気書院）
　　　　　　　大槻富之助　著　数�Vの研究（旺文社））