円順列 
最近、「円順列の確率」で円順列の計算に触れる機会があった。ふと気が付くと、当HPに
適当な円順列をまとめたページがないということで、これをまとめてみようと思い立った。
当HPには、群論の知識を用いた、バーンサイドの定理による円順列の数え上げのページ
「円順列の数え上げ」もあるのだが、専門的すぎて実際の受験で活用が難しいと思い、バー
ンサイドの定理によらない、「周期」の概念を用いた解法を中心に整理したいと思う。
円順列と順列の違い
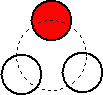
赤玉1個と白玉2個がある。
順列とは、これらを横一列に並べた場合の数で、3!/(2!1!)=3通り ある。



円順列とは、順列で得られた場合を円形に並べた場合の数で、回転して重なるものは同
じものとみなされ、この場合は、1通りしかない。
円順列の求め方
次の2つがよく知られた方法である。
(1) 1つを固定して回転を止め、固定されたもの以外の順列を数える方法
赤玉1個を固定して考えると、他は白玉2個。この白玉2個の順列の数は、1通り
(2) 回転は止めないで、回転して重なるものを数える方法



において、赤玉の位置を1個ずつずらしていくと、丁度3回目の操作で元に戻る。これを
周期といい、この場合、周期は3である。
これらを円形に並べると、回転して重なるものは同じと見なして、

の1通りが出来るが、これを軌道といい、円順列の個数は、この軌道の数のことである。
すなわち、赤玉1個と白玉2個の円順列の個数は、
(軌道の数)=(順列の数)/(周期)
から、 3÷3=1(通り) で求められる。
教科書的には、次の公式が知られている。
異なるn個の円順列の個数は、 (n-1)!通り
(証明) 方法(1)を用いれば、1個を固定して、残りのn-1個の順列を考えればいいので、
求める円順列の個数は、(n-1)!通り
方法(2)を用いれば、周期nの順列がn!個できるので、軌道の個数は、
n!/n=(n-1)!(通り) (証終)
異なるものの円順列に比べて、円形に並べるものに同じものが含まれている場合は、単
純に計算できない場合が多い。そこで、基本的な問題パターンを通して、同じものを含む円
順列の求め方を把握し、その理解を深めよう。
問題 赤玉、白玉、青玉、黒玉各1個ずつの円順列の個数を求めよ。
この場合は、方法(1)、方法(2)の両方が使える。
(解) 方法(1) → 赤玉を固定して、他の3個の順列は、3!=6(通り)
方法(2) → 赤玉、白玉、青玉、黒玉各1個ずつの順列の個数は、4!=24(通り)
赤玉、白玉、青玉、黒玉各1個ずつの順列の周期は、4なので、
求める円順列の個数は、 24/4=6(通り) (終)
問題 赤玉1個、白玉2個、青玉2個の円順列の個数を求めよ。
この場合は、方法(1)の方が有効だろう。
(解) 赤玉1個を固定して考えると、求める場合の数は、白玉2個、青玉2個の順列の個数
に等しいので、 4!/(2!2!)=6(通り) (終)
以下の問題では、方法(1)は無力で、方法(2)の方が有効である。
問題 赤玉2個、白玉2個の円順列の個数を求めよ。
(解) 赤玉2個、白玉2個の順列の個数は、 4!/(2!2!)=6(通り)
赤玉2個、白玉2個の順列には、周期が4のものと、周期が2のものがある。
周期が2の順列の個数は、赤玉1個、白玉1個の順列の個数なので、2!=2(個) あり、
それ以外の順列は、周期4である。
したがって、求める円順列の個数は、 2/2+(6-2)/4=1+1=2(通り) (終)
問題 赤玉3個、白玉3個の円順列の個数を求めよ。
(解) 赤玉3個、白玉3個の順列の個数は、 6!/(3!3!)=20(通り)
赤玉3個、白玉3個の順列には、周期が6のものと、周期が2のものがある。
周期が2の順列の個数は、赤玉1個、白玉1個の順列の個数なので、2!=2(個) あり、
それ以外の順列は、周期6である。
したがって、求める円順列の個数は、 2/2+(20-2)/6=1+3=4(通り) (終)
問題 赤玉4個、白玉4個の円順列の個数を求めよ。
(解) 赤玉4個、白玉4個の順列の個数は、 8!/(4!4!)=70(通り)
赤玉4個、白玉4個の順列には、周期が8のものと周期が2のものがある。
周期が2の順列の個数は、赤玉1個、白玉1個の順列の個数なので、2!=2(個) あり、
周期が4の順列の個数は、赤玉2個、白玉2個の順列の個数なので、
4!/(2!2!)=6(個) あるが、この中には周期2のものも含まれているので、実質4通り、
それ以外の順列は、周期8である。したがって、求める円順列の個数は、
2/2+4/4+(70-6)/8=1+1+8=10(通り) (終)
(コメント) 周期4の順列の中に周期2の順列が潜り込んでいるところが難しいですね!
問題 赤玉2個、白玉2個、青玉2個の円順列の個数を求めよ。
(解) 赤玉2個、白玉2個、青玉2個の順列の個数は、 6!/(2!2!2!)=90(通り)
赤玉2個、白玉2個、青玉2個の順列には、周期が6のものと、周期が3のものがある。
周期が3の順列の個数は、赤玉1個、白玉1個、青玉1個の順列の個数なので、
3!=6(個) あり、それ以外の順列は、周期6である。
したがって、求める円順列の個数は、 6/3+(90-6)/6=2+14=16(通り) (終)
問題 赤玉4個、白玉2個、青玉2個の円順列の個数を求めよ。
この問題は、ずっと昔の東京大学の入試問題らしい。
(解) 赤玉4個、白玉2個、青玉2個の順列の個数は、 8!/(4!2!2!)=420(通り)
赤玉4個、白玉2個、青玉2個の順列には、周期が8、周期が4のものがある。
周期が4の順列の個数は、赤玉2個、白玉1個、青玉1個の順列の個数なので、
4!/2!=12(個) あり、それ以外の順列は、周期8である。
したがって、求める円順列の個数は、12/4+(420-12)/8=3+51=54(通り) (終)
これまでの計算から、周期から軌道を求める方法は、万能な...予感!高校生の時は、
あまりこのような計算はしたことがないというか、避けていたので、すべてが新鮮ですね。
一般に、赤玉m個、白玉n個の円順列の個数は、mとnが互いに素のとき、
(m+n)!/(m!n!) 通り
で求められる。mとnが互いに素でないとき、方法(2)が有効で、万能である。
読者のために、練習問題を残しておこう。
練習問題 赤玉6個、白玉3個の円順列の個数を求めよ。
(解) 赤玉6個、白玉3個の順列の個数は、 9!/(6!3!)=84(通り)
赤玉6個、白玉3個の順列には、周期が9のものと周期が3のものがある。
周期が3の順列の個数は、赤玉2個、白玉1個の順列の個数なので、3!/2!=3(個)
あり、それ以外の順列は、周期9である。したがって、求める円順列の個数は、
3/3+(84-3)/9=1+9=10(通り) (終)
慶應義塾大学医学部(2018)で、次のような問題が出題されている。
問題 k を自然数とする。赤玉と白玉がそれぞれ2k個ずつある。これらをすべて円周上
に等間隔に並べる並べ方の総数をNk とおく。このとき、N1、N2、N3 の値を求めよ。
ただし、回転して並びが同じになるものは同じ並べ方と考える。
(解) k=1のとき、赤玉2個、白玉2個の順列の個数は、4!/(2!2!)=6(通り)
赤玉2個、白玉2個の順列には、周期が4のものと、周期が2のものがある。
周期が2の順列の個数は、赤玉1個、白玉1個の順列の個数なので、2!=2(個) あり、
それ以外の順列は、周期4である。
したがって、求める円順列の個数は、 2/2+(6-2)/4=1+1=2(通り)
k=2のとき、赤玉4個、白玉4個の順列の個数は、8!/(4!4!)=70(通り)
赤玉4個、白玉4個の順列には、周期が8のものと周期が2のものがある。
周期が2の順列の個数は、赤玉1個、白玉1個の順列の個数なので、2!=2(個) あり、
周期が4の順列の個数は、赤玉2個、白玉2個の順列の個数なので、
4!/(2!2!)=6(個) あるが、この中には周期2のものも含まれているので、実質4通り、
それ以外の順列は、周期8である。したがって、求める円順列の個数は、
2/2+4/4+(70-6)/8=1+1+8=10(通り) (終)
k=3のとき、赤玉6個、白玉6個の順列の個数は、12!/(6!6!)=924(通り)
赤玉6個、白玉6個の順列には、周期が12のもの、周期が6のもの、周期が4のもの、
周期が2のものがある。
周期が2の順列の個数は、赤玉1個、白玉1個の順列の個数なので、2!=2(個) あり、
周期が4の順列の個数は、赤玉2個、白玉2個の順列の個数なので、
4!/(2!2!)=6(個) あるが、この中には周期2のものも含まれているので、実質4通り、
周期が6の順列の個数は、赤玉3個、白玉3個の順列の個数なので、
6!/(3!3!)=20(個) あるが、この中には周期2のものも含まれているので、
実質18通り、それ以外の順列は、周期12である。したがって、求める円順列の個数は、
2/2+4/4+18/6+(924-6-18)/12=1+1+3+75=80(通り) (終)
問題 赤玉3個、白玉3個、青玉3個の円順列の個数を求めよ。
この問題は、数学オリンピック予選(2003)で出題されている。
(解) 赤玉3個、白玉3個、青玉3個の順列の個数は、9!/(3!3!3!)=1680(通り)
赤玉3個、白玉3個、青玉3個の順列には、周期が9、周期が3のものがある。
周期が3の順列の個数は、赤玉1個、白玉1個、青玉1個の順列の個数なので、
3!=6(個) あり、それ以外の順列は、周期9である。
したがって、求める円順列の個数は、6/3+(1680-6)/9=2+186=188(通り) (終)
問題 赤玉4個、白玉2個の円順列の個数を求めよ。
(解) 赤玉4個、白玉2個の順列の個数は、6!/(4!2!)=15(通り)
赤玉4個、白玉2個の順列には、周期が6、周期が3のものがある。
周期が3の順列の個数は、赤玉2個、白玉1個の順列の個数なので、3!/(2!)=3(個)
あり、それ以外の順列は、周期6である。
したがって、求める円順列の個数は、3/3+(15-3)/6=1+2=3(通り) (終)
(別解) 白玉の状態で場合分けすれば、
(1) 白玉2個が隣り合う場合
(2) 白玉2個の間に赤玉1個が入る場合
(3) 白玉2個の間に赤玉2個が入る場合(すなわち、白玉2個が向かい合う場合)
の3通りしかないので、求める円順列の個数は、3通り (終)
問題 赤玉4個、白玉8個の円順列の個数を求めよ。
(解) 赤玉4個、白玉8個の順列の個数は、12!/(4!8!)=495(通り)
赤玉4個、白玉8個の順列には、周期が12、周期が6、周期が3のものがある。
周期が3の順列の個数は、赤玉1個、白玉2個の順列の個数なので、3!/(2!)=3(個)
あり、周期が6の順列の個数は、赤玉2個、白玉4個の順列の個数なので、
6!/(2!4!)=15(個)あるが、この中には周期3のものも含まれているので、
実質12通りあり、それ以外の順列は、周期12である。
したがって、求める円順列の個数は、
3/3+12/6+(495-15)/12=1+2+40=43(通り) (終)
#43通りの中には、線対称なものが 6C2=15(通り) あり、残りの28通りが非線対称で
ある。したがって、数珠順列の個数は、 15+28/2=29(通り) となる。
ところで、「赤玉4個、白玉8個の順列には、周期が12、周期が6、周期が3のものがある」
は、次のようにして求められる。
4と8の公約数を求めて、1、2、4 から、周期は、 12/1、12/2、12/4 すなわち、
周期 12、6、3 となる。
裏返しが可能な場合は、裏返して同じになるものが出てくる。それらを同一のものと考える
考え方が、数珠順列である。(上記の問題の#を参照)
異なるn個の円順列の個数は、(n-1)!(個)であったが、3以上のnについて、異なるn
個の数珠順列の個数は、(n-1)!/2 (個) で求められる。
#n=1の場合に円順列を考えることは、まずない。
n=2の場合、円順列の個数は、1通りで、数珠順列も1通りとなる。
(すなわち、(n-1)!/2という公式は適用できない。)
DD++ さんからのコメントです。(令和5年11月12日付け)
意外と難しいのが数珠順列で、簡単そうに見えて非常に間違えやすい。円順列で考えたと
きに、線対称なものが 2 個 1 組になるのは n≧3 のときだけなのを忘れがち。
(コメント) DD++さん、ご指摘ありがとうございます。2個以下の場合は全く想定外でした!
上記は、修正済みです。
同じものを含む数珠順列では、線対称なものと、非線対称なものに分けて考えるのが基本
である。(上記の問題の#を参照)
問題 赤玉1個、白玉2個、青玉2個を円形に並べる。
(1) 円順列の個数を求めよ。
(2) 数珠順列の個数を求めよ。
(解)(1) 赤玉1個を固定して、白玉2個、青玉2個の順列の数に等しいので、
4!/(2!2!)=6(通り)
(2) 赤玉を基準に、左右に白玉、青玉が並ぶ場合の2通りは、線対称である。
それ以外の 6-2=4(通り) は非線対称である。
したがって、求める数珠順列の数は、 2+4/2=4(通り) (終)
問題 赤玉1個、白玉2個、青玉6個の数珠順列の個数を求めよ。
(解) 赤玉1個を固定して、白玉2個、青玉6個の順列の数は、8!/(2!6!)=28(通り)
赤玉を基準に、左右に白玉1個、青玉3個が並ぶ場合の4通りは、線対称である。
それ以外の 28-4=24(通り) は非線対称である。
したがって、求める数珠順列の数は、 4+24/2=16(通り) (終)
問題 赤玉1個、白玉4個、青玉8個の数珠順列の個数を求めよ。
(解) 赤玉1個を固定して、白玉4個、青玉8個の順列の数は、
12!/(4!8!)=495(通り)
赤玉を基準に、左右に白玉2個、青玉4個が並ぶ場合の6!/(2!4!)=15(通り)は、
線対称である。それ以外の 495-15=480(通り) は非線対称である。
したがって、求める数珠順列の数は、 15+480/2=255(通り) (終)
問題 赤玉3個、白玉2個、青玉2個の数珠順列の個数を求めよ。
(解) 赤玉3個、白玉2個、青玉2個の順列は、7!/(3!2!2!)=210(通り)
3、2、2 は互いに素なので、周期7のもののみ。
よって、求める円順列は、 210/7=30(通り)
赤玉の1個を固定して、左右に、赤玉1個、白玉1個、青玉1が並ぶ場合の数は、
3!=6(通り)
よって、求める数珠順列の個数は、 6+(30-6)/2=6+12=18(通り) (終)
問題 赤玉2個、白玉2個、青玉2個、黄玉2個の数珠順列の個数を求めよ。
(解) 赤玉2個、白玉2個、青玉2個、黄玉2個の順列は、
8!/(2!2!2!2!)=2520(通り)
周期8のものと周期が4のものがある。
周期が4の順列の個数は、赤玉1個、白玉1個、青玉1個、黄玉1個の順列の個数なので、
4!=24(個)あり、それ以外の順列は、周期8である。
よって、求める円順列の個数は、 24/4+(2520-24)/8=6+312=318(通り)
このうち、左右対称な円順列の個数は、赤玉1個、白玉1個、青玉1個、黄玉1個の順列の
個数に等しく、4!=24(通り)ある。
よって、求める数珠順列の個数は、24+(318-24)/2=24+147=171(通り) (終)
問題 赤玉2個、白玉3個、青玉4個がある。次の問いに答えよ。
(1) 円順列の個数を求めよ。
(2) 青玉が隣り合わない円順列の個数を求めよ。
(3) 9個から4個選んで円形に並べる場合の数を求めよ。
(解)(1) 赤玉2個、白玉3個、青玉4個の順列の個数は、
9!/(2!3!4!)=1260(通り)
2、3、4は、互いに素なので、周期は9のみ。
よって、求める円順列の個数は、 1260/9=140(通り)
(2) 赤玉2個、白玉3個の順列の個数は、5!/(2!3!)=10(通り)
2、3は互いに素なので、周期は5のみ。
よって、赤玉2個、白玉3個の円順列の個数は、10/5=2(通り)
そのうちの1通りに対して、5個の隙間から4個選んで青玉を入れる場合の数は、5通り
よって、求める円順列の個数は、 2×5=10(通り)
(3) 青玉4個の円順列は、1通り
青玉3個+赤玉1個 または 青玉3個+白玉1個 の円順列は、 1×2=2(通り)
青玉2個+赤玉2個 または 青玉2個+白玉2個 の円順列は、
(2/2+(6-2)/4)×2=4(通り)
青玉2個+赤玉1個+白玉1個 の円順列は、3通り
青玉1個+赤玉2個+白玉1個 または 青玉1個+赤玉1個+白玉2個 または
青玉1個+白玉3個の円順列は、
3×2+1=7(通り)
赤玉2個+白玉2個の円順列は、 2通り
赤玉1個+白玉3個の円順列は、 1通り
以上から、求める円順列の個数は、 1+2+4+3+7+2+1=20(通り) (終)
ここで、典型的で、ちょっと変わった円順列の問題をまとめておこう。
問題 男子3人、女子3人の円順列を考える。
(1) 円順列の総数を求めよ。
(2) 男女が交互に並ぶ円順列の個数を求めよ。
(解)(1) (6-1)!=5!=120(通り)
(2) まず、男子3人を円形に並べる場合の数は、 (3-1)!=2!=2(通り)
そのうちの1通りに対して、女子3人を男子の間に入れる場合の数は、3!=6(通り)
よって、求める場合の数は、 2×6=12(通り) (終)
問題 男子4人、女子2人の円順列を考える。
(1) 女子が隣り合う場合の数を求めよ。
(2) 女子2人が向かい合う場合の数を求めよ。
(3) 女子2人の間に男子1人が入る場合の数を求めよ。
(解)(1) 女子2人を1人と見て、5人の円順列の個数は、(5-1)!=4!=24(通り)
その1通りに対して、女子の順番を考えて、求める場合の数は、
24×2!=48(通り)
(2) 女子2人を円形に並べる場合の数は、(2-1)!=1(通り)
その1通りに対して、男子4人の順列の総数は、4!=24(通り)
よって、求める場合の数は、 1×24=24(通り)
(3) 女子2人の間に入る男子の選び方は、4通り
その1通りに対して、女子2人と男子1人を1人と見て、(3+1)人の円順列の総数は、
(4-1)!=3!=6(通り)
その1通りに対して、女子の順番を考えて、求める場合の数は、
4×6×2!=48(通り) (終)
問題 男子5人、女子2人が円形に並ぶとき、女子2人が隣り合わない円順列の個数を求
めよ。
(解) 男子5人、女子2人の円順列の個数は、 (7-1)!=720(通り)
このうち、女子2人が隣り合う場合の数は、 (6-1)!×2=240(通り)
よって、求める場合の数は、 720-240=480(通り) (終)
(別解) 男子5人の円順列の個数は、(5-1)!=24(通り)
そのうちの1通りに対して、女子2人を1人ずつ男子の隙間に入れる場合の数は、
5P2=20(通り)
よって、求める場合の数は、 24×20=480(通り) (終)
問題 正三角形のテーブルに9人が着席する方法は何通りあるか。ただし、テーブルの各
辺には3人ずつ着席するものとする。
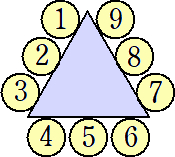
(解) 9人の円順列は、(9-1)!=8!=40320(通り)
そのうちの1通りに対して、正三角形のテーブルに着席する方法は、3通りある。
よって、求める場合の数は、 40320×3=120960(通り) (終)
問題 正方形のテーブルに8人が着席する方法は何通りあるか。ただし、テーブルの各
辺には2人ずつ着席するものとする。
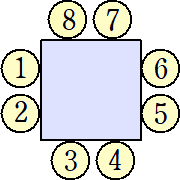
(解) 8人の円順列は、(8-1)!=7!=5040(通り)
そのうちの1通りに対して、正方形のテーブルに着席する方法は、2通りある。
よって、求める場合の数は、 5040×2=10080(通り) (終)
問題 長方形のテーブルに6人が着席する方法は何通りあるか。ただし、テーブルに対し
て、3人と3人が対面するものとする。
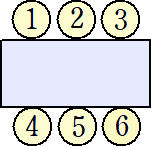
(解) 6人の円順列は、(6-1)!=5!=120(通り)
そのうちの1通りに対して、長方形のテーブルに着席する方法は、3通りある。
よって、求める場合の数は、 120×3=360(通り) (終)
(別解) 6人の順列は、6!=720(通り)
このとき、3人ずつ対面で着席するとき、123456 と 654321 は同じ場合の数になる。
よって、求める場合の数は、 720÷2=360(通り) (終)
問題 立方体について、次の問いに答えよ。ただし、回転により一致するものは、同じもの
とみなすものとする。
(1) 立方体の各面に、1~6の番号を記入するとき、何通りの方法があるか。ただし、異な
る面には異なる数字を記入するものとする。
(2) 立方体の各頂点に、1~8の番号を記入するとき、何通りの方法があるか。ただし、異
なる頂点には異なる数字を記入するものとする。
(解)(1) 立方体の上面に数字1を記入し固定するとき、下面の数字の記入方法は、5通
りあり、そのうちの1通りに対して、側面に番号を記入する方法は、4個の円順列に等しく、
(4-1)!=3!=6(通り)
よって、求める場合の数は、 5×6=30(通り)
(2) 立方体の上面を固定し、その頂点に記入された4個の数字の順列は、
(4-1)!=3!=6(通り) で、そのうちの1通りに対して、残りの4個の数字を下面の4
頂点に記入する方法は、4!=24(通り) ある。
よって、求める場合の数は、 6×24=144(通り) (終)
大学入試センター試験(1997)の追試験で、次のような問題が出題(改題)された。
問題 大小2つの円卓がある。大の円卓には4つの席があり、小の円卓には3つの席が
ある。この円卓に、A、B、C、D、E、Fの6人が分かれて着席する方法を考える。ただし、
円卓を回転して同じ座り方は同じものとみなすことにする。
このとき、次の問いに答えよ。
(1) 2つの円卓に3人ずつ座る方法は何通りか。
(2) 4人と2人に座る方法は何通りか。
(3) Aが小の円卓に座るとき、Aの隣りに空席が出来る座り方は何通りか。
(4) Aが大の円卓に座るとき、Aの隣りに空席が出来る座り方は何通りか。
(5) A、Bが同じ円卓に座る方法は何通りか。
(解)(1) 大の円卓に座る3人を選んで、空席を固定して3人を座らせる方法は、
6C3×3!=20×6=120(通り)
そのうちの1通りに対して、小の円卓に3人を座らせる方法は、(3-1)!=2!=2(通り)
よって、求める場合の数は、 120×2=240(通り)
(2) 小の円卓に座る2人を選んで、空席を固定して2人を座らせる方法は、
6C2×2!=15×2=30(通り)
そのうちの1通りに対して、大の円卓に4人を座らせる方法は、(4-1)!=3!=6(通り)
よって、求める場合の数は、 30×6=180(通り)
(3) 小の円卓に座る1人を選んで、空席を固定して2人を座らせる方法は、
5C1×2!=5×2=10(通り)
そのうちの1通りに対して、大の円卓に4人を座らせる方法は、(4-1)!=3!=6(通り)
よって、求める場合の数は、 10×6=60(通り)
(4) 大の円卓に座る2人を選んで、Aの隣りが空席になるように3人を座らせる方法は、
5C2×4=10×4=40(通り)
そのうちの1通りに対して、小の円卓に3人を座らせる方法は、(3-1)!=2!=2(通り)
よって、求める場合の数は、 40×2=80(通り)
(5) AとBが大の円卓に座るとき、残り4人が
(大,小)=(2,2) のとき、4C2×(4-1)!×2!=72(通り)
(大,小)=(1,3) のとき、4C1×3!×(3-1)!=48(通り)
AとBが小の円卓に座るとき、残り4人が
(大,小)=(4,0) のとき、(4-1)!×2!=12(通り)
(大,小)=(3,1) のとき、4C1×(3-1)!×3!=48(通り)
よって、求める場合の数は、 72+48+12+48=180(通り) (終)
問題 6人が円形に並ぶとき、特定の3人が隣り合う場合の数を求めよ。
(解) 特定の3人を1人とみて、4人の円順列は、(4-1)!=6(通り)
そのうちの1通りに対して、特定の3人の順列は、3!=6(通り)
よって、求める場合の数は、 6×6=36(通り) (終)
問題 8人の中に、2組の夫婦がいる。8人が円形に並ぶとき、夫婦は必ず隣り合って並
ぶようにする。並べ方は何通りあるか。
(解) 2組の夫婦をそれぞれ1人とみて、6人の円順列の個数は、
(6-1)!=5!=120(通り)
このうちの1通りに対して、それぞれの夫婦の順列は、2!×2!=4(通り)
よって、求める場合の数は、 120×4=480(通り) (終)
問題 赤玉と白玉が合わせて7個ある。これらを用いて数珠を作るとき、何通りできるか。
ただし、使わない色があってもよいものとする。
(解) (赤玉,白玉)=(7,0)のとき、1通り
(赤玉,白玉)=(0,7)のとき、1通り
(赤玉,白玉)=(6,1)のとき、1通り
(赤玉,白玉)=(1,6)のとき、1通り
(赤玉,白玉)=(5,2)のとき、7!/(5!2!)=21(通り)で、すべて周期7なので、
円順列の個数は、21/7=3(通り) これらはすべて左右対称なので、数珠順列の個数は、
3通りとなる。
(赤玉,白玉)=(2,5)のとき、7!/(2!5!)=21(通り)で、すべて周期7なので、
円順列の個数は、21/7=3(通り) これらはすべて左右対称なので、数珠順列の個数は、
3通りとなる。
(赤玉,白玉)=(4,3)のとき、7!/(4!3!)=35(通り)で、すべて周期7なので、
円順列の個数は、35/7=5(通り) このうち左右対称なものは、3通りで、残りの2通りは
左右非対称。よって、数珠順列の個数は、3+2/2=4(通り)となる。
(赤玉,白玉)=(3,4)のとき、7!/(3!4!)=35(通り)で、すべて周期7なので、
円順列の個数は、35/7=5(通り) このうち左右対称なものは、3通りで、残りの2通りは
左右非対称。よって、数珠順列の個数は、3+2/2=4(通り)となる。
以上から、求める場合の数は、
1+1+1+1+3+3+4+4=18(通り) (終)
問題 1、2、3の3個から重複を許して4個取り、円形に並べる方法の数を求めよ。
(解) 1111、2222、3333のそれぞれの場合、1通り
1112、1113、1222、2223、1333、2333のそれぞれの場合、1通り
1122、1133、2233のそれぞれの場合、4!/(2!2!)=6(通り) のうち、周期2のも
のが2通りで、残り4通りは周期が4。よって、円順列の個数は、2/2+4/4=2(通り)
1123、1223、1233の場合、4!/2!=12(通り) のすべてが周期4なので、
円順列の個数は、12/4=3(通り)
以上から、求める場合の数は、
1×3+1×6+2×3+3×3=24(通り) (終)
異なる n 個のものから重複を許して r 個とる順列の数は、重複順列と言われ、公式は、
nΠr=nr (通り) で求められる。異なる n 個のものから重複を許して r 個とる組合せの数
は、重複組合せと言われ、公式は、nHr=n+r-1Cr 通りで求められる。
同様のことが円順列でもあるということを最近知ることができた。
異なる n 個のものから重複を許して r 個とる円順列の数は、重複円順列と言われ、公式
は、 (1/r)Σk=1r n(k,r) ただし、(k,r) は k と r の最大公約数
証明は、バーンサイドの定理を用いて示される。
問題 1、2、3の3個から重複を許して4個取り、円形に並べる方法の数を求めよ。
に、公式を適用してみよう。
(別解) 求める場合の数は、
(1/4)Σk=14 3(k,4)=(31+32+31+34)/4=96/4=24(通り) (終)
読者のために、練習問題を置いておこう。
練習問題 赤玉、白玉、青玉、黄玉から重複を許して6個とる円順列の数を求めよ。
(解) 求める場合の数は、
(1/6)Σk=16 4(k,6)
=(41+42+43+42+41+46)/6=4200/6=700(通り) (終)
#場合分けで解こうとしたら、あまりの煩雑さに挫折...。
次の問題は、数学オリンピック予選(2002)の問題(改題)です。並べ方に条件があって、
難問といってもいいでしょう。
問題 赤・白・青・黄の4色で下図を塗り分ける。同じ色を何回も使ってよいし、4色すべて
を使う必要はないが、隣り合う2つの扇形は異なる色で塗り分けるものとする。
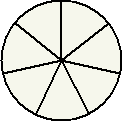
何通りの塗り分け方があるだろうか?ただし、回転して重なる塗り方は同じものとみなす。
(解) 7つの順列を考える。
これらを、問題の条件:「隣り合うものは異なる色で塗り分ける」を満たすものが何通りある
かを数える。ただし、①と⑦は異なる色で塗るものとする。
求める場合の数が an 通りあるものとする。
(1) ①と⑥が異なる色のとき、①②③④⑤⑥の塗り方は、an-1 通りあり、そのうちの1通り
に対して、⑦の塗り方は、2通りあるので、この場合の塗り方は、2an-1 通りである。
(2) ①と⑥が同じ色のとき、①②③④⑤の塗り方は、an-2 通りあり、そのうちの1通りに
対して、⑦の塗り方は、3通りあるので、この場合の塗り方は、3an-2 通りである。
以上から、 an=2an-1+3an-2 が成り立つ。
ここで、明らかに、a1=0 、a2=12 なので、
a3=2a2+3a1=2・12+3・0=24
a4=2a3+3a2=2・24+3・12=84
a5=2a4+3a3=2・84+3・24=240
a6=2a5+3a4=2・240+3・84=732
a7=2a6+3a5=2・732+3・240=2184
これらはすべて周期7なので、求める円順列の個数は、 2184/7=312(通り) (終)
(補足) 上記では、漸化式 a1=0 、a2=12 、an=2an-1+3an-2 を帰納的に用いた
が、もちろん直接的に解くことも可能である。
特性方程式 x2-2x-3=0 を解いて、(x-3)(x+1)=0 より、x=3、-1
よって、 an-3an-1=-(an-1-3an-2) から、an-3an-1=12・(-1)n
また、 an+an-1=3(an-1+an-2) から、an+an-1=4・3n-1
よって、 4an=4・3n+12・(-1)n から、 an=3n+3・(-1)n
したがって、赤・白・青・黄の4色でn個に等分割された扇形を塗り分ける。同じ色を何回も
使ってよいし、4色すべてを使う必要はないが、隣り合う2つの扇形は異なる色で塗り分け
るものとするとき、回転して重なる塗り方は同じものとみなして、求める円順列の個数は、
(3n+3・(-1)n)/n (通り)
であることが分かる。
問題 赤玉4個、白玉4個、青玉4個の数珠順列の個数を求めよ。
(解) 赤玉4個、白玉4個、青玉4個の順列は、
12!/(4!4!4!)=34650(通り)
周期12のもの、周期6のもの、周期3のものがある。
周期が3の順列の個数は、赤玉1個、白玉1個、青玉1個の順列の個数なので、
3!=6(個)あり、周期が6の順列の個数は、赤玉2個、白玉2個、青玉2個の順列の個数
なので、6!/(2!2!2!)=90(通り)あり、このうち、6通りは周期3のものと重複する。
これら以外の順列は、周期12である。
よって、求める円順列の個数は、
6/3+(90-6)/6+(34650-90)/12=2+14+2880=2896(通り)
このうち、左右対称な円順列の個数は、赤玉2個、白玉2個、青玉2個の順列の個数に等し
く、6!/(2!2!2!)=90(通り)ある。
よって、求める数珠順列の個数は、
90+(2896-90)/2=90+1403=1493(通り) (終)
以下、工事中!






