
丂崅峑偵擖妛偟偰悢妛傪妛廗偟偰偄偔拞偱丄拞妛峑悢妛偲偺戝偒側堘偄偼丄晄摍幃偺埖偄
偩傠偆丅拞妛峑偱偼丄愄偵斾傋晄摍幃偺埖偄偼寉帇偝傟傞孹岦偵偁傞偺偱丄崅峑偱丄岻柇
側晄摍幃偺巊偄夞偟偵捈柺偡傞偲丄堄奜偵屗榝偭偰偟傑偆惗搆偑懡偄丅
丂傑偢偼丄寉偄弨旛塣摦偐傜丅
栤戣丂丂係偮偺幚悢 倎丄倐丄們丄倓 偵懳偟偰丄倎亄倐亄們亄倓亖係 偑惉傝棫偮偲偒丄彮側偔
丂丂丂丂偲傕堦偮偼 侾 埲忋偱偁傞偙偲傪帵偣丅
乮夝乯丂偡傋偰偑 侾 傛傝彫偝偄丄偡側傢偪丄倎 亙侾丄倐 亙侾丄們 亙侾丄倓 亙侾 偲壖掕偡傞偲丄
丂倎 亄 倐 亄 們 亄 倓 亙係丂偲側傞偑丄偙傟偼丄忦審偵柕弬偡傞丅
丂傛偭偰丄彮側偔偲傕堦偮偼 侾 埲忋偱偁傞丅丂乮廔乯
乮僐儊儞僩乯丂埲慜丄搶嫗彈巕戝妛偺擖帋栤戣偵摨條偺栤戣偑弌戣偝傟偨丅攚棟朄偱峫偊傞
丂丂丂丂丂丂偙偲偼丄偛偔帺慠側敪憐偩傠偆丅
丂偦傟偱偼丄師偺栤戣偼偳偆偩傠偆偐丠
栤戣丂丂偡傋偰偑 侽 偱側偄 値 屄偺幚悢 倎1 亝 倎2 亝丒丒丒亝 倎値 偑丄
丂丂丂倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値 亖 侽
丂傪枮偨偡偲偒丄丂 倎1亄 俀倎2亄 俁倎3 亄 丒丒丒 亄 値倎値亜侽丂偑惉傝棫偮偙偲傪帵偣丅
丂忋偺栤戣偱丄 乽 倎1 丄 倎2 丄丒丒丒 偑廫暘彫偝偐偭偨傜丄尵偊側偄応崌偑偁傞偺偱偼丠乿偲巚
偭偰偟傑偆偑丄倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値 亖 侽 偲偄偆忦審偑堄奜偵尩偟偔丄乽偦傫側偙偲偼側
偔丄昁偢惉傝棫偮両乿偙偲偑師偺傛偆偵偟偰帵偝傟傞丅
乮夝乯丂倎1 亝 倎2 亝丒丒丒亝 倎値丂偐偮丂倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値 亖 侽丂偑惉傝棫偮偺偱丄
丂偁傞悢 倠 乮 俀亝 倠 亝 値 乯偑懚嵼偟偰丄
丂倎1 亙侽丂丄丂倎1 亝 倎2 亝丒丒丒亝 倎倠-1亝 侽 亙 倎倠亝丒丒丒亝 倎値
偦偙偱丄丂俙倣亖倎倣亄 倎倣+1 亄丒丒丒 亄 倎値丂丂乮 侾亝 倣 亝 値 乯丂丂偲偍偔偲丄
丂倎1亄 俀倎2亄 俁倎3 亄 丒丒丒 亄 値倎値 亖 俙1亄 俙2亄 俙3亄丒丒丒亄 俙値
亖 俙2亄 俙3亄丒丒丒亄 俙値丂丂乮仼丂俙1亖侽 乯
偲彂偗傞丅
丂偟偨偑偭偰丄戣堄傪帵偡偨傔偵偼丄俙倣亜侽丂乮 俀亝 倣 亝 値 乯傪帵偣偽傛偄丅
丂俀 亝 倣 亝 倠亅侾丂偺偲偒丄丂俙倣亖亅乮倎1亄 倎2亄 丒丒丒 亄 倎倣-1乯亜 侽
丂倠 亝 倣 亝 値丂偺偲偒丄丂丂俙倣亖倎倣亄 倎倣+1 亄丒丒丒 亄 倎値亜 侽
埲忋偐傜丄丂丂俙倣亜侽丂丂乮 俀亝 倣 亝 値 乯丂偑帵偝傟偨丅
丂傛偭偰丄丂倎1亄 俀倎2亄 俁倎3 亄 丒丒丒 亄 値倎値亜侽丂偑惉傝棫偮丅丂乮廔乯
乮僐儊儞僩乯丂忋婰偺夝偺拞偱丄乽俙倣亖倎倣亄 倎倣+1 亄丒丒丒 亄 倎値丂乮 侾亝 倣 亝 値 乯乿傪峫偊傞
丂丂丂丂丂偙偲偑億僀儞僩偵側偭偰偄傞丅
丂倎1亄 俀倎2亄 俁倎3 亄 丒丒丒 亄 値倎値
亖倎1亄 倎2亄 倎3 亄 丒丒丒 亄 倎値
丂丂丂亄 倎2亄 倎3 亄 丒丒丒 亄 倎値
丂丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亄 倎値
偲偄偆帺慠側敪憐偑婎杮偩傠偆偑丄傾乕儀儖偺憤榓岞幃傪梡偄偰傕丄帺慠偵乽俙倣乿偑弌尰偡
傞偙偲偑暘偐傞丅偡側傢偪丄
丂倎1亄 俀倎2亄 俁倎3 亄 丒丒丒 亄 値倎値
亖乮倎1亄 倎2亄 倎3 亄 丒丒丒 亄 倎値乯値
丂丂亅倎1
丂丂亅倎1亅 倎2
丂丂丒丒丒丒丒丒丒丒丒丒丒
丂丂亅倎1亅 倎2亅 倎3 亅 丒丒丒 亅 倎値-1
亖俙2亄 俙3亄丒丒丒亄 俙値
偱偁傞丅偙偺娭學傪梡偄偰丄忋婰偲摨條偵晄摍幃偺惉傝棫偮偙偲偑帵偝傟傞丅
丂師偺栤戣傕嫽枴怺偄丅
栤戣丂丂値 屄偺幚悢 倎1 丄倎2 丄丒丒丒 丄倎値 偑丄丂倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値 亖 値丂傪
丂丂枮偨偡偲偒丄丂倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2 亞 値丂偑惉傝棫偮偙偲傪帵偣丅
丂忋偺栤戣傕丄 乽 倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値 亖 値丂乿偑旕忢偵尩偟偄忦審偱丄榓偑 値 偩偭
丂偨傜丄偦傟偧傟偺暯曽偺榓偼昁偢丄値 埲忋偱側偗傟偽側傜側偄偲偄偆偙偲傪帵偟偰偄傞丅
丂侽 亝 倎倠 亝 侾 偵懳偟偰偼丄丂倎倠2 亝 倎倠丂偑惉傝棫偮偺偱丄侽 亝 倎倠 亝 侾 傪枮偨偡悢偑
憡摉悢娷傑傟傟偽丄乽尵偊側偄応崌偑偁傞偺偱偼丠乿偲巚偭偰偟傑偆偑丄乽偦傫側偙偲偼側偔丄
昁偢惉傝棫偮両乿偙偲偑師偺傛偆偵偟偰帵偝傟傞丅
乮夝乯丂値乮倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2乯亅乮倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値乯2
亖乮値亅侾)( 倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2乯亅俀乮倎1丆倎2丆丒丒丒丆倎値 偺憡堎側傞俀崁偺愊偺榓乯
亖乷 乮倎倣亅 倎値乯2丂(扐偟丄倣亗値)丂偺榓 乸亞侽
傛偭偰丄値乮倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2乯亞乮倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値乯2
傛傝丄丂丂倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2 亞 値丂丂偑惉傝棫偮丅丂丂乮廔乯
乮僐儊儞僩乯丂偙偺栤戣傪丄悢妛揑婣擺朄偱徹柧偟傛偆偲偟偨偑丄嵙愜偟偰偟傑偭偨両
丂傑偨丄僔儏儚儖僣偺晄摍幃丗
丂乮倎12亄倎22亄丒丒丒亄倎値2)(倃12亄倃22亄丒丒丒亄倃値2乯亞乮倎1倃1亄倎2倃2亄 丒丒丒亄倎値倃値乯2
傪抦偭偰偄傟偽丄倃1亖倃2亖丒丒丒亖倃値亖侾 偲偟偰丄捈偪偵忋婰偺晄摍幃偼帵偝傟傞丅
丂僔儏儚儖僣偺晄摍幃偼丄
丂儀僋僩儖 兛 亖乮倎1丆倎2丆丒丒丒丆倎値乯丄兝 亖乮倃1丆倃2丆丒丒丒丆倃値乯丂偵偍偄偰丄
丂撪愊 丗 兛 丒 兝 亖| 兛 || 兝 |們倧倱兤丂乮 兤 偼丄 兛 丄 兝 偺側偡妏乯傪梡偄偰丄
丂| 兛 || 兝 |亞| 兛 丒 兝 |
偲昞偝傟傞丅
乮嶲峫暥專丗揷搰丂柅丂挊丂丂揷搰偺悢妛嘥丂乮墵暥幮乯乯
丂僔儏儚儖僣偺晄摍幃丂乮儼兛倠2乯乮儼兝倠2乯亞乮儼兛倠兝倠乯2丂傪帵偡偵偼丄
俴倎倗倰倎値倗倕偺峆摍幃丂丂擟堄偺幚悢兛倠丄兝倠偵懳偟偰丄
丂乮儼兛倠2乯乮儼兝倠2乯亅乮儼兛倠兝倠乯2亖儼乮兛倞兝倠亅兛倠兝倞乯2
摍偑梡偄傜傟傞丅傑偨丄幚悢倲偵偮偄偰丄掕晞崋偺愨懳晄摍幃 | 倲兛亅兝 |2亞侽 偱敾暿幃傪
梡偄偰傕娙扨偵帵偝傟傞丅
丂俴倎倗倰倎値倗倕偺峆摍幃傪徹柧偡傞応崌丄峴楍幃傪梡偄偰帵偡偲尒捠偟傛偔徹柧偱偒傞丅
丂倎亖乮兛倠乯丄倐亖乮兝倠乯偲偡傞偲丄俴倎倗倰倎値倗倕偺峆摍幃偼丄
丂嵍曈亖倓倕倲乮乷倎丒倎丂倎丒倐乸丆乷倐丒倎丂倐丒倐乸乯亖儼倓倕倲乮乷兛倞丂兛倠乸丆乷兝倞丂兝倠乸乯2亖塃曈
偲帵偝傟傞丅
丂忋婰偺夝偵懳偟偰丄暯惉俀侾擭俉寧俁侽擔晅偗偱丄俫丏俬丏偝傫偵師偺傛偆側暿夝偑偁傞偙偲傪
偛嫵帵偄偨偩偄偨丅俫丏俬丏偝傫偵姶幱偟傑偡丅乮懡彮丄暥尵摍偼廋惓偝偣偰偄偨偩偒傑偟偨丅乯
乮暿夝乯丂倎1丄 倎2丄 倎3丄丒丒丒丄 倎値丂偼幚悢側偺偱丄柧傜偐偵
丂乮倎1亅侾乯2亄乮 倎2亅侾乯2亄乮 倎3亅侾乯2 亄丒丒丒 亄乮 倎値亅侾乯2 亞 侽
偑惉傝棫偮丅丂偙偙偱丄丂倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値 亖 値丂側偺偱丄
嵍曈亖倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2亅俀乮倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値乯亄値
丂亖倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2亅値丂丂偱偁傞丅
傛偭偰丄丂倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2亅値亞侽丂丂偐傜丄
丂倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2 亞 値丂丂偑惉傝棫偮丅丂丂乮廔乯
乮僐儊儞僩乯丂乮倎1亅侾乯2亄乮 倎2亅侾乯2亄乮 倎3亅侾乯2 亄丒丒丒 亄乮 倎値亅侾乯2 亞 侽丂傪巚偄偮偐傟
丂丂丂丂丂偨偙偲偵姶摦偟傑偟偨丅偙偺晄摍幃偺懚嵼偱丄埲屻偺徹柧偑慡偔帺慠偱丄偦偺旤偟偝
丂丂丂丂丂偼寁傝抦傟側偄偱偡偹両
乮捛婰乯丂暯惉俀俇擭侾侾寧俁侽擔晅偗
丂僀僃儞僛儞偺晄摍幃偺偙偲傪抦偭偰偄傟偽丄師偺傛偆側暿夝傕壜擻偩傠偆丅
乮暿夝乯丂俥乮倶乯亖倶2 偼壓偵撌偺娭悢側偺偱丄僀僃儞僛儞偺晄摍幃傛傝丄
丂乷倖乮倎1乯亄倖乮倎2乯亄丒丒丒亄倖乮倎値乯乸/値亞倖乮乮倎1亄倎2亄丒丒丒亄倎値乯/値乯
偡側傢偪丄丂乮倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2乯/値亞乮乮倎1亄倎2亄丒丒丒亄倎値乯/値乯2
倎1亄 倎2亄 倎3 亄丒丒丒 亄 倎値亖値丂傛傝丄乮倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2乯/値亞侾
傛偭偰丄丂倎12亄 倎22亄 倎32 亄 丒丒丒 亄 倎値2 亞 値丂丂偑惉傝棫偮丅丂丂乮廔乯
乮捛婰乯丂暯惉俀侽擭侾俀寧俀俆擔晅偗
丂忋婰偺栤戣偵娭楢偟偰丄師偺傛偆側栤戣傕嫽枴怺偄丅
栤戣丂丂幚悢 倎丄倐丄們 偵懳偟偰丄丂倎 亄 倐 亄 們 亖 俀丂丄丂倎2 亄 倐2亄 們2 亖 係
丂偑惉傝棫偮偲偒丄倎 偺嵟戝抣傪媮傔傛丅
乮夝乯丂倐 亄 們 亖 俀 亅 倎丂丄丂倐2亄 們2 亖 係 亅 倎2丂側偺偱丄僔儏儚儖僣偺晄摍幃傛傝丄
丂乮侾2亄 侾2乯乮倐2亄 們2乯亞乮倐 亄 們乯2
傛偭偰丄丂俀乮係 亅 倎2乯亞乮俀 亅 倎乯2丂傛傝丄丂俁倎2 亅 係倎 亅係 亝 侽
乮俁倎亅俀乯乮倎亅俀乯亝侽丂傪夝偄偰丄俀/俁亝倎亝俀丂傛傝丄倎 偺嵟戝抣偼丄俀丂丂乮廔乯
乮僐儊儞僩乯丂忋婰偺傛偆偵丄僔儏儚儖僣偺晄摍幃傪梡偄偨夝朄偼丄曄悢偺屄悢偑偄偔偮偱傕
丂丂丂丂桳岠側曽朄偱偁傞丅
丂曄悢偺屄悢偑俁屄側偺偱丄師偺傛偆側夝朄傕偁傞偑丄偦偺桪楎偼柧傜偐偩傠偆丅
乮暿夝乯丂倐2亄 們2 亖 乮倐 亄 們乯2 亅 俀倐們 亖 係 亅 倎2丂傛傝丄
丂俀倐們 亖 乮俀 亅 倎乯2 亅 係 亄 倎2 亖 俀倎2 亅 係倎丂偡側傢偪丄丂倐們 亖 倎2 亅 俀倎
偙偺偲偒丄丂倐 丄們 偼丄俀師曽掱幃丂倲2亅乮俀亅倎乯倲亄倎2亅俀倎亖侽丂偺幚悢夝偲側傞丅
傛偭偰丄敾暿幃傪俢偲偡傞偲丄俢亖乮俀 亅 倎乯2亅係乮倎2亅俀倎乯亞侽丂偐傜丄
丂俁倎2 亅 係倎 亅係 亝 侽丂偐傜丄丂俀/俁亝倎亝俀
偟偨偑偭偰丄丂倎 偺嵟戝抣偼丄俀丂丂乮廔乯
乮捛婰乯丂堦尒偟偰惓偟偄偐偳偆偐敾慠偲偟側偄偑丄堄枴偑暘偐傞偲惓偟偄偙偲偑慛傗偐偵
丂丂丂丂丂丂棟夝偱偒傞師偺晄摍幃偼奆偝傫傕偳偙偐偱偍栚偵偐偐偭偰偄傞偙偲偩傠偆丅
栤戣丂丂倎亞倐亜侽丂丄倃亞倄亜侽丂偺偲偒丄丂倎倃亄倐倄亞倎倄亄倐倃丂偑惉傝棫偮偙偲傪帵偣丅
丂丂傑偨丄摍崋偑惉傝棫偮偺偼丄丂倎亖倐丂傑偨偼丂倃亖倄丂偺偲偒偵尷傞偙偲傪帵偣丅
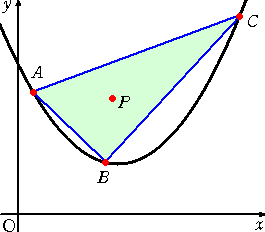
亙恾傪梡偄偨捈姶揑愢柧亜
丂壓恾傪偠偭偲尒偮傔偰偄傞偲丄晄摍幃偺堄枴偑慛傗偐偵棟夝偱偒傞偙偲偱偟傚偆丅
丂
丂偙偺恾傪梡偄偨徹柧傪傒偨傜丄師偺傛偆側戙悢揑側徹柧偼丄偲偰傕枴婥側偔姶偠傜傟傞丅
乮徹柧乯丂丂乮倎倃亄倐倄乯亅乮倎倄亄倐倃乯亖倎乮倃亅倄乯亅倐乮倃亅倄乯亖乮倎亅倐乯乮倃亅倄乯亞侽
丂丂摍崋惉棫偼丄倎亅倐亖侽丂傑偨偼丂倃亅倄亖侽丂偺偲偒偵尷傞丅
丂戙悢揑側徹柧偼丄暣傟偑側偄妋幚側徹柧曽朄偩偑丄偄傠偄傠側恖傪愢摼偡傞偵偼撻愼傑
側偄偟丄偦偺晄摍幃偺恀偺堄枴偑棟夝偝傟偨偐偳偆偐傕暘偐傜側偄丅恾偱帵偝傟傞偲丄乽偆傫丄
偦偆偩偹両乿偲怱偲恎懱偑弖帪偵崌揰偟偰偟傑偆偲偙傠偑丄恾偺帩偮枺椡側偺偩傠偆丅
丂側偍丄偙偺晄摍幃偵偍偄偰丄丂倎亖倃丂丄倐亖倄丂偲偍偔偲丄
丂丂倎2亄倐2亞俀倎倐
偑摼傜傟傞丅偙傟偼丄憡壛暯嬒偲憡忔暯嬒偺娭學幃偱丄偙偺偙偲偐傜丄丂倎倃亄倐倄亞倎倄亄倐倃丂
偲偄偆晄摍幃偺丄晄摍幃偺悽奅偵偍偗傞埵抲偯偗偑暘偐傞偺偱偼側偄偩傠偆偐丠
乮嶲峫暥專丗丂惣尦嫵慞丂挊
丂憡壛憡忔暯嬒偺晄摍幃傪嶻傒弌偡崻尮揑晄摍幃偵偮偄偰丂乮悢尋捠怣乯乯
乮捛婰乯 暯惉侾俋擭俈寧俈擔晅偗
丂崱擔偼幍梉丅廗偄帠偺忋払傪婅偭偨峴帠傕崱偱偼偡偭偐傝彜嬈僀儀儞僩偲壔偟偰偄傞丅彫
妛峑帪戙丄嶚偺梩偵婅偄帠傪彂偄偨抁嶜傪偔偔傝偮偗偨偺偑夰偐偟偄丅乮娬榖媥戣乯
丂幚悢 倶丄倷丄倸 偵懳偟偰丄晄摍幃丂倶2亄倷2亄倸2亞倶倷亄倷倸亄倸倶丂偑惉傝棫偮偙偲偼丄庴
尡栤戣廤傪昍夝偄偨曽側傜扤偱傕侾搙偼偍栚偵偐偐偭偰偄傞偲巚偆丅
丂徹柧偼堈偟偄偑丄弶傔偰偦偺徹柧偵怗傟傞曽偵偼庒姳晘嫃偑崅偄偐傕偟傟側偄丅
丂俀乮倶2亄倷2亄倸2亅倶倷亅倷倸亅倸倶乯亖乮倶亅倷乯2亄乮倷亅倸乯2亄乮倸亅倶乯2亞侽丂傛傝丄
丂倶2亄倷2亄倸2亞倶倷亄倷倸亄倸倶
偑惉傝棫偮丅摿偵丄忋婰偺徹柧偐傜柧傜偐側傛偆偵丄摍崋偑惉傝棫偮偺偼丄倶亖倷亖倸偺偲偒
偵尷傞丅
丂嵟嬤丄偙偺桳柤側晄摍幃偺寗娫傪杽傔傞幃偑偁傞偙偲傪抦偭偨丅
丂幚悢 倶丄倷丄倸 偵懳偟偰丄
丂
慜敿偺晄摍崋偼丄僔儏儚儖僣偺晄摍幃
丂乮倎2亄倐2亄們2乯乮倶2亄倷2亄倸2乯亞乮倎倶亄倐倷亄們倸乯2
偐傜帺柧偩傠偆丅乮丂倎亖倐亖們亖侾丂偲偍偗偽傛偄丅乯
屻敿偺晄摍崋偼丄晄摍幃 倶2亄倷2亄倸2亞倶倷亄倷倸亄倸倶 偦偺傕偺偱偁傞丅
丂忋婰偺晄摍幃偺慜敿晹暘傪彂偒捈偡偲丄
丂
偡側傢偪丄
丂
偱偁傞偑丄偝傜偵丄幚悢 倶丄倷丄倸 傪惓偺悢偵尷掕偡傞偲丄
丂
偑惉傝棫偮偺偱丄寢嬊丄惓偺悢 倶丄倷丄倸 偵懳偟偰
丂
偱偁傞偙偲偑暘偐傞丅
丂忋婰偺悇榑偺棳傟偺拞偱丄
丂
偲偄偆晄摍幃偼帺柧偲偼尵偊側偄偩傠偆丅
乮徹柧乯丂俁乮倶3亄倷3亄倸3乯亅乮倶2亄倷2亄倸2乯乮倶亄倷亄倸乯
亖俀倶3亄俀倷3亄俀倸3亅倶2倷亅倶倷2亅倷2倸亅倷倸2亅倸2倶亅倸倶2
亖乮倶3亅倶2倷亅倶倷2亄倷3乯亄乮倷3亅倷2倸亅倷倸2亄倸3乯亄乮倸3亅倸2倶亅倸倶2亄倶3乯
亖乮倶亅倷乯乮倶2亅倷2乯亄乮倷亅倸乯乮倷2亅倸2乯亄乮倸亅倶乯乮倸2亅倶2乯
亖乮倶亅倷乯2乮倶亄倷乯亄乮倷亅倸乯2乮倷亄倸乯亄乮倸亅倶乯2乮倸亄倶乯亞侽
傛傝丄晄摍幃偺惉傝棫偮偙偲偑帵偝傟偨丅
丂摍崋偑惉棫偡傞偺偼丄倶亖倷亖倸丂偺偲偒偵尷傞丅丂乮徹廔乯
乮捛婰乯丂暯惉俀俇擭侾侾寧俁侽擔晅偗
丂忋婰偺晄摍幃
丂
偼丄僀僃儞僛儞偺晄摍幃傛傝帺柧偱偁傠偆偑丄師偺傛偆側帵偟曽傕偁傞丅
丂倶丄倷丄倸 偑惓悢偺偲偒丄丂俋乮倶3亄倷3亄倸3乯亞乮倶亄倷亄倸乯3丂偑惉傝棫偮丅
乮徹柧乯丂僔儏儚儖僣偺晄摍幃丂乮倎2亄倐2亄們2乯乮倶2亄倷2亄倸2乯亞乮倎倶亄倐倷亄們倸乯2丂偱丄
丂倎亖倐亖們亖侾丂偲偍偗偽丄丂俁乮倶2亄倷2亄倸2乯亞乮倶亄倷亄倸乯2
偝傜偵丄僔儏儚儖僣偺晄摍幃丂乮倎2亄倐2亄們2乯乮倶2亄倷2亄倸2乯亞乮倎倶亄倐倷亄們倸乯2丂偱丄
丂倎丄倐丄們 偵丄倶3/2丄倷3/2丄倸3/2 傪戙擖丄倶丄倷丄倸 偵丄併倶丄併倷丄併倸 傪戙擖偟偰丄
丂乮倶3亄倷3亄倸3乯乮倶亄倷亄倸乯亞乮倶2亄倷2亄倸2乯2
傛偭偰丄丂乮倶3亄倷3亄倸3乯乮倶亄倷亄倸乯亞乮倶亄倷亄倸乯4/俋丂傛傝丄
丂俋乮倶3亄倷3亄倸3乯亞乮倶亄倷亄倸乯3丂丂乮徹廔乯
丂偙偺晄摍幃偼丄師偺傛偆偵堦斒壔偝傟傞丅
丂惓偺悢 倶丄倷丄倸 偲帺慠悢 倣丄値丂偵懳偟偰
丂
丂徹柧偼忋婰偲摨條偱偁傞丅
乮徹柧乯丂俁乮倶倣亄値亄倷倣亄値亄倸倣亄値乯亅乮倶倣亄倷倣亄倸倣乯乮倶値亄倷値亄倸値乯
亖俀倶倣亄値亄俀倷倣亄値亄俀倸倣亄値亅倶倣倷値亅倶値倷倣亅倷倣倸値亅倷値倸倣亅倸倣倶値亅倸値倶倣
亖乮倶倣亄値亅倶倣倷値亅倶値倷倣亄倷倣亄値乯亄乮倷倣亄値亅倷倣倸値亅倷値倸倣亄倸倣亄値乯
丂亄乮倸倣亄値亅倸倣倶値亅倸値倶倣亄倶倣亄値乯
亖乮倶値亅倷値乯乮倶倣亅倷倣乯亄乮倷値亅倸値乯乮倷倣亅倸倣乯亄乮倸値亅倶値乯乮倸倣亅倶倣乯
偙偙偱丄徹柧偡傋偒晄摍幃偼丄 倶丄倷丄倸 偵懳偟偰懳徧側偺偱丄丂倶亞倷亞倸丂偲偟偰傕堦斒惈傪
幐傢側偄丅偙偺偲偒丄丂倶倣亞倷倣亞倸倣丂丄倶値亞倷値亞倸値丂側偺偱丄
丂乮倶値亅倷値乯乮倶倣亅倷倣乯亄乮倷値亅倸値乯乮倷倣亅倸倣乯亄乮倸値亅倶値乯乮倸倣亅倶倣乯亞侽
傛傝丄晄摍幃偺惉傝棫偮偙偲偑帵偝傟偨丅
摍崋偑惉棫偡傞偺偼丄倶亖倷亖倸丂偺偲偒偵尷傞丅丂乮徹廔乯
乮僐儊儞僩乯丂嬒惍偺偲傟偨旤偟偄晄摍幃偱偡偹両
丂忋婰偱帵偟偨晄摍幃丗丂惓偺悢 倶丄倷丄倸 偵懳偟偰
丂
傪堦斒壔偡傟偽丄
丂惓偺悢 倶丄倷丄倸 偲帺慠悢 値丂偵懳偟偰
丂
偲側傞丅乮仼偲偰傕旤偟偄晄摍幃偱偡偹両乯
丂偙偺帠幚偼丄娭悢 俥乮倶乯亖倶値丂乮値亜侾乯偑撌娭悢偱偁傞偙偲傪梡偄偰帵偝傟傞丅
傑偢丄撌娭悢偺偙偲傪傑偲傔偰偍偙偆丅
丂娭悢 倷亖俥乮倶乯 偑撌娭悢偱偁傞偲偼丄偦偺僌儔僼偑撌恾宍偺偲偒傪偄偆丅捈娤揑偵偼丄僌
儔僼忋偺擟堄偺揰偱丄偦偺揰傪捠傞捈慄傪堷偒丄僌儔僼偑偦偺捈慄偺曅曽偵偺傒偁傞傛偆
偵弌棃傞応崌傪偄偆丅乮仺 嶲徠 丗 撌恾宍偺婎慴抦幆乯
丂傑偨丄撌娭悢偺僌儔僼偼師偺惈幙傪帩偮丅
丂僌儔僼忋偺擟堄偺俀揰 俙丄俛 傪寢傇慄暘俙俛偵偍偄偰丄慄暘俙俛忋偺擟堄偺揰 俹 偼僌儔僼
忋傑偨偼忋曽乮僌儔僼忋傑偨偼壓曽乯偵偁傞丅
丂曻暔慄 倷亖倶2丂傗 倷亖亅倶2丂偺僌儔僼傪僀儊乕僕偡傟偽棟夝偟傗偡偄偩傠偆丅
倷亖倶2丂偼丄壓偵撌側娭悢丄倷亖亅倶2丂偼丄忋偵撌側娭悢偱偁傞丅
丂偙偺偙偲傪晄摍幃傪梡偄偰昞偣偽埲壓偺傛偆偵側傞丅
倷亖俥乮倶乯 偑壓偵撌側娭悢偱偁傞偲偒丄
丂僌儔僼忋偺擟堄偺俀揰 俙乮倎丆俥乮倎乯乯丄俛乮倐丆俥乮倐乯乯 偲幚悢 倲丂乮侽亝倲亝侾乯偵懳偟偰丄
丂乮侾亅倲乯丒俥乮倎乯亄倲丒俥乮倎乯亞俥乮乮侾亅倲乯倎亄倲倐乯
偑惉傝棫偮丅乮忋偵撌側娭悢傕摨條偱丄偙偺応崌偼晄摍崋偼媡岦偒偵側傞丅乯
椺丂晄摍幃丂乥倶亄倷乥亝乥倶乥亄乥倷乥丂偑惉傝棫偮偙偲傪帵偣丅
丂偙偺晄摍幃偼捠忢偼椉曈偺暯曽偺嵎傪偲傞偙偲偵傛傝帵偝傟傞偑丄撌娭悢偺惈幙傪梡偄
傟偽丄偦偺堄枴偑柧傜偐偲側傞丅
乮徹柧乯丂娭悢 俥乮倶乯亖乥倶乥偼壓偵撌側娭悢側偺偱丄幚悢 倲丂乮侽亝倲亝侾乯偵懳偟偰丄
丂乮侾亅倲乯乥倶乥亄倲乥倷乥亞乥乮侾亅倲乯倶亄倲倷乥
偙偙偱丄丂倲亖侾/俀丂偲偡傟偽丄柧傜偐偵丄乥倶乥亄乥倷乥亞乥倶亄倷乥偑惉傝棫偮丅丂丂乮徹廔乯
乮僐儊儞僩乯丂扨側傞戙悢偺栤戣偲巚偄偒傗娭悢偺惈幙偲枾愙偵娭學偟偰偄傞偲偼悢妛偼墱
丂丂丂丂丂偑怺偄偱偡偹丅
丂忋婰偱偼丄撌娭悢偺僌儔僼忋偺俀揰偵娭偡傞晄摍幃傪帵偟偨偑丄俁揰偺応崌偼師偺傛偆
偵側傞丅乮仺丂嶲峫 丗 僀僃儞僛儞偺晄摍幃乯
丂倷亖俥乮倶乯 偑壓偵撌側娭悢偱偁傞偲偒丄
丂僌儔僼忋偺擟堄偺俁揰 俙乮倎丆俥乮倎乯乯丄俛乮倐丆俥乮倐乯乯丄俛乮倐丆俥乮倐乯乯 偵懳偟偰丄
幚悢 倫丄倯丄倰丂偑丄丂倫丄倯丄倰亞侽丂丄倫亄倯亄倰亗侽丂傪枮偨偡偲偒丄
丂
偑惉傝棫偮丅
丂倫亄倯亖侾丄倰亖侽丂偺応崌偑挌搙俀揰偺応崌偱偁傞丅
丂徹柧偼丄壓恾
丂
偵偍偄偰丄仮俙俛俠偺撪晹偍傛傃廃忋偺揰俹偺嵗昗偑
丂
丂乮偨偩偟丄丂倫丄倯丄倰亞侽丂丄倫亄倯亄倰亗侽丂乯
偲昞偝傟傞偙偲偐傜柧傜偐偱偁傠偆丅
丂偙偺岞幃傪梡偄傟偽丄惓偺悢 倶丄倷丄倸 偲帺慠悢 値丂偵懳偟偰丄娭悢 俥乮倶乯亖倶値丂偼壓偵撌
側娭悢側偺偱丄
丂
偲側傞偙偲偑梕堈偵暘偐傞丅
丂偝偰丄晄摍幃丂乥倶亄倷乥亝乥倶乥亄乥倷乥丂傪梡偄偨墳梡偱丄師偺晄摍幃偼柺敀偄丅
丂倎丄倐 偑幚悢偺偲偒丄
丂
丂偙偺徹柧傪戙悢揑偵張棟偡傞偺偼戝曄偦偆側偺偱丄傗偼傝娭悢偺惈幙偺偛栵夘偵側偭偨
曽偑傛偝偦偆偩丅
乮徹柧乯丂娭悢 俥乮倶乯亖倶/乮侾亄倶乯丂偵懳偟偰丄偦偺摫娭悢 俥乫乮倶乯亖侾/乮侾亄倶乯2亜侽丂側偺偱
扨挷偵憹壛偡傞丅丂傛偭偰丄丂丂乥倎亄倐乥亝乥倎乥亄乥倐乥丂側偺偱丄
丂
偑惉傝棫偮丅
丂傑偨丄娭悢 俧乮倶乯亖侾/乮侾亄倶乯丂偵懳偟偰丄偦偺摫娭悢 俧乫乮倶乯亖亅侾/乮侾亄倶乯2亙侽
側偺偱扨挷偵尭彮偡傞丅
傛偭偰丄乥倎乥亝乥倎乥亄乥倐乥丄乥倐乥亝乥倎乥亄乥倐乥側偺偱丄
丂
偑惉傝棫偮丅丂偙偺偲偒丄
丂
側偺偱丄
丂
偑惉傝棫偮丅丂乮徹廔乯
乮僐儊儞僩乯丂徹柧偺曽朄偑偲偰傕怴慛偱偡偹両
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偐傜偺弌戣偱偡丅
乮暯惉俀係擭侾寧侾俇擔晅偗乯
栤戣丂丂倶丄倷丄倸 偼惓偺幚悢偱丄倶倷倸亖係丂偺偲偒丄
丂丂(倶亄倷亄倸)乷倶3/(倶亄倷乯亄倷3/(倷亄倸)亄倸3/(倸亄倶)乸亞侾俉
傪徹柧偟側偝偄丅
丂倶倷倸亖侾丂側傜偽丄乽Nesbitt 偺晄摍幃乿偱徯夘偝傟偰偄傞晄摍幃偺夝朄恀帡偨傜偱偒傞偐傕
偟傟傑偣傫偑丄偙偙偺幃偵偼丄倶3 偑偁偭偨傝丄倶倷倸亖係 偩偐傜偳偆傗偭偨傜偄偄偺偐暘偐傜偢
丏丏丏丅
丂俥俶偝傫偑徹柧偝傟傑偟偨丅乮暯惉俀係擭侾寧侾俈擔晅偗乯
丂乽憡壛暯嬒亞憡忔暯嬒乿偩偗偱偱偒傑偡丅
乮夝乯丂倶亄倷亄倸亖倱丄倶倷倸亖倲丂偲偍偔丅
丂俹亖倶3/(倶亄倷乯亄倷3/(倷亄倸)亄倸3/(倸亄倶)丂偲偍偔偲丄乽憡壛暯嬒亞憡忔暯嬒乿傛傝丄
丂俹亞俁乷倶3倷3倸3/(倶亄倷乯(倷亄倸)(倸亄倶)乸1/3亖俁倶倷倸/乷(倶亄倷乯(倷亄倸)(倸亄倶)乸1/3
丂亖俁倲/乷(倶亄倷乯(倷亄倸)(倸亄倶)乸1/3
嵞傃丄乽憡壛暯嬒亞憡忔暯嬒乿傛傝丄
乷(倶亄倷乯(倷亄倸)(倸亄倶)乸1/3亝乷(倶亄倷乯亄(倷亄倸)亄(倸亄倶)乸/俁亖俀倱/俁
媡悢傪偲偭偰丄丂侾/乷(倶亄倷乯(倷亄倸)(倸亄倶)乸1/3亝俁/乮俀倱乯
傛偭偰丄丂嵍曈亖倱俹亞倱丒俋倲/乮俀倱乯亖俋倲/俀
丂倲亖係丂側偺偱丄丂嵍曈亞侾俉丂丂乮廔乯
乮仸乯丂倶倷倸亖係丂偲偄偆偺偼偪傚偭偲曄側愝掕偱偡偹丅倶倷倸亖侾偐倶倷倸亖俀偱偄偄偲巚偄傑偡丅
丂傛偍偡偗偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭侾寧侾俈擔晅偗乯
丂FN偝傫丄夝摎偁傝偑偲偆偛偞偄傑偡丅偁偺栤戣偼丄2007擭偛傠摉帪崅峑1擭惗偩偭偨巕偑
塣塩偟偰偄偨僒僀僩偱徯夘偝傟偨帺嶌栤戣偺1偮偱偡丅惓夝偺応崌偼宱尡抣侾侽傪梌偊傞丄
偲偄偆傕偺偱偟偨丅尰嵼偼儕儞僋愗傟偐暵嵔偺偨傔僒僀僩偼徚偊偰偟傑偄傑偟偨丅嶌偭偨杮恖
偵傛傞偲夝偔偺偵俁擔偐偐偭偨偲偺偙偲偱偡丅
丂傛偍偡偗偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭侾寧侾俈擔晅偗乯
丂FN偝傫偺夝摎傪尒偰丄乽Nesbitt 偺晄摍幃乿偺儁乕僕偺夝朄偺夁掱傪尒偰偄偨傜丄師偺傛偆
偵偱偒傑偟偨丅
乮夝乯丂乽憡壛暯嬒亞憡忔暯嬒乿偺娭學傛傝丄
丂俀乮倶亄倷亄倸乯亖(倶亄倷乯亄(倷亄倸)亄(倸亄倶)亞俁乷(倶亄倷乯(倷亄倸)(倸亄倶)乸1/3
丂倶3/(倶亄倷乯亄倷3/(倷亄倸)亄倸3/(倸亄倶)亞俁倶倷倸/乷(倶亄倷乯(倷亄倸)(倸亄倶)乸1/3
椉曈傪偦傟偧傟偐偗偰丄
丂俀乮倶亄倷亄倸乯乷倶3/(倶亄倷乯亄倷3/(倷亄倸)亄倸3/(倸亄倶)乸亞俋倶倷倸
側偺偱丄丂乮倶亄倷亄倸乯乷倶3/(倶亄倷乯亄倷3/(倷亄倸)亄倸3/(倸亄倶)乸亞乮俋/俀乯倶倷倸
丂傛偭偰丄丂倶倷倸亖係丂傪戙擖偡傞偲丄
丂乮倶亄倷亄倸乯乷倶3/(倶亄倷乯亄倷3/(倷亄倸)亄倸3/(倸亄倶)乸亞侾俉
丂摍崋惉棫偼丄倶亄倷亖倷亄倸亖倸亄倶丂偡側傢偪丄丂倶亖倷亖倸丂偺偲偒惉傝棫偮丅
丂偙偙偱偼丄倶亖倷亖倸亖係1/3丂丂乮廔乯
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭侾寧侾俉擔晅偗乯
丂傛偍偡偗偝傫偺夝朄偺曽偑帺慠偱偄偄偱偡偹丅
丂倶亄倷亄倸 偲偄偆偺偼丄(倶亄倷乯亄(倷亄倸)亄(倸亄倶) 偺敿暘偩偭偨偺偱偡偹丅偙偺偙偲偵婥偑偮
偗偽娙扨偱偡偑丄婥偑偮偒傑偣傫偱偟偨丅
丂(A亄B亄C)(倶3/A亄倷3/B亄倸3/C)亞俋倶倷倸
偲彂偄偰傒傞偲丄傎偲傫偳柧傜偐偵尒偊傑偡丅僐乕僔乕丒僔儏儚儖僣偺姶偠傕偟傑偡偑丄乽憡壛
暯嬒亞憡忔暯嬒乿偺娭學傪俀夞偺曽偑偄偄傛偆偱偡丅
丂偳偆偱傕偄偄偙偲偱偡偑丄倶倷倸亖係丂偲偄偆忦審偑撲偱偡丅倶倷倸亖侾 偐 俀 偲偡傞偐丄塃曈偑丄
乮俋/俀乯倶倷倸丂偺幃偺傑傑偐偑晛捠偱偟傚偆丅偁傞偄偼丄倶亄倷亄倸亖侾丂偺偲偒傪偮偗偰嵍曈傪
傕偆彮偟尒傗偡偔偡傞偐丏丏丏丅