イェンゼンの不等式 　　　　　　　　　　　　　　　　　　　　　　　

　高校で学ぶ不等式で、相加平均と相乗平均の関係は単純ながら、その応用の豊富さに
驚かされる。私の一番のお気に入りは、

　「　ｘ＞０　のとき、　ｘ＋１/ｘ の最小値を求めよ。　」　（こちらを参照）

である。高校１年のときに初めて、この問題が相加平均と相乗平均の関係を用いて鮮やか
に解決されるのに遭遇して、そのアクロバットさゆえに数学の奥深さに感じ入ったものだ。

　相加平均と相乗平均の関係とは、

　ａ≧０ 、ｂ≧０ に対して、

　

というものであった。

　上記は項の数が２個の場合であるが、一般には、

　　のとき、

　

という不等式が成り立つ。

　これらの不等式の証明は、２個の場合は平易だが、一般の場合は少し複雑である。

　ものは試しに証明に挑戦してみよう！　証明は、数学的帰納法を用いる。

（証明）　ｎ＝２　のとき、

　

より、命題は成り立つ。

　ｎ＝２^ｐ　（ｐ≧１）のとき成り立つと仮定する。

　ｎ＝２^ｐ＋1　のとき、隣り合う２項ずつを組み合わせて、ｎ＝２　のときの結果を用いれば、

　　ｎ＝２^ｐ　（ｐ≧１）の場合に還元でき、

　　

　

より、命題は成り立つ。

　以上から、全ての自然数 ｐ について、　ｎ＝２^ｐ　のとき、命題は成り立つ。

　２以上の任意の自然数 ｎ に対して、　２^ｐ-1＜ｎ≦２^ｐ　となる自然数 ｐ が存在する。

　いま、　２^ｐ−ｎ＝ｍ　とおくと、　２^ｐ＝ｍ＋ｎ　である。

そこで、

　

とおくと、

　

よって、　　　　なので、　

したがって、

　

が成り立つ。　　（証終）


（コメント）　．．．かなり技巧的な証明ですね！でも、感動しました！！


　実は、これらの不等式を統一的に証明する方法がある。それは上記の不等式の何れも
が、Ｊｅｎｓｅｎ の不等式の特別の場合だからである。

　Ｊｅｎｓｅｎ の不等式から、相加平均と相乗平均の関係、シュワルツの不等式やヘルダー
の不等式を導くことが出来る。その意味で、「Ｊｅｎｓｅｎ の不等式」は、最も基本的な不等
式であると言えよう。

Ｊｅｎｓｅｎ の不等式（１９０６年）

　関数 ｆ（ｘ） は、凸関数とする。このとき、

　λ₁＋λ₂＋・・・＋λ_ｎ＝１　を満たすλ₁≧０、λ₂≧０、・・・、λ_ｎ≧０　に対して　


　λ₁ｆ（ｘ₁）＋λ₂ｆ（ｘ₂）＋・・・＋λ_ｎｆ（ｘ_ｎ）≧ｆ（λ₁ｘ₁＋λ₂ｘ₂＋・・・＋λ_ｎｘ_ｎ）

が成り立つ。

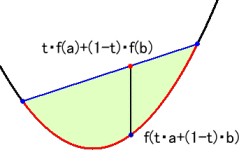
　ここで、関数 ｆ（ｘ） が、凸関数であるとは、

任意の ａ、ｂ と ０≦ ｔ ≦１ を満たす ｔ に対して、ｔ・ｆ（ａ）＋(１−ｔ)・ｆ（ｂ）≧ｆ（ｔ・ａ＋(１−ｔ)・ｂ）　

が成り立つときを言う。

　もしも、関数 ｆ（ｘ） が２回微分可能ならば、次の定理により、凸関数か否かが判定できる。

　関数 ｆ（ｘ） において、ｆ”（ｘ）≧０　ならば、関数 ｆ（ｘ） は凸関数である

　このことは、グラフ的には、次のような意味がある。

　グラフ上のどんな２点を選んでも、それらを結ぶ線分の下方に対応する部分のグラフ
がある
　

凸関数の例

（１）　区間 （−∞ ，∞） において、関数 ｆ（ｘ）＝ ｘ^2ｎ

（２）　区間 [０ ，π] において、関数 ｆ（ｘ）＝−ｓｉｎ ｘ

（３）　区間 [−π/２ ，π/２] において、関数 ｆ（ｘ）＝−ｃｏｓ ｘ

（４）　区間 [０ ，π/２） において、関数 ｆ（ｘ）＝ｔａｎ ｘ

（５）　区間 （０ ，∞） において、関数 ｆ（ｘ）＝−ｌｏｇ ｘ

　凸関数（ｃｏｎｖｅｘ）の定義から、「−」がどうしてもついてしまう場合があるが、それを回避
するために、凹関数（ｃｏｎｃａｖｅ）も同様にして定義される。

　Ｊｅｎｓｅｎ の不等式は、凸関数を定義する不等式を一般化したものである。

実際に、ｔ・ｆ（ａ）＋(１−ｔ)・ｆ（ｂ）≧ｆ（ｔ・ａ＋(１−ｔ)・ｂ）において、ｔ＝λ₁、１−ｔ＝λ₂ とおくと、

　λ₁≧０、λ₂≧０　、λ₁＋λ₂＝１　で、　λ₁ｆ（ｘ₁）＋λ₂ｆ（ｘ₂）≧ｆ（λ₁ｘ₁＋λ₂ｘ₂）

となり、これは、Ｊｅｎｓｅｎ の不等式の ｎ＝２ の場合である。

ｎ＝３　のときは、どうだろうか？確認してみよう。

　λ₁≧０、λ₂≧０、λ₃≧０　で、λ₁＋λ₂＋λ₃＝１　とする。

このとき、

λ₁ｆ（ｘ₁）＋λ₂ｆ（ｘ₂）＋λ₃ｆ（ｘ₃）

＝λ₁ｆ（ｘ₁）＋（λ₂＋λ₃）［｛（λ₂/（λ₂＋λ₃）｝ｆ（ｘ₂）＋｛λ₃/（λ₂＋λ₃）｝ｆ（ｘ₃）］

　ここで、　λ₂/（λ₂＋λ₃）＋λ₃/（λ₂＋λ₃）＝１　なので、

｛（λ₂/（λ₂＋λ₃）｝ｆ（ｘ₂）＋｛λ₃/（λ₂＋λ₃）｝ｆ（ｘ₃）
≧ｆ（｛λ₂/（λ₂＋λ₃）｝ｘ₂＋｛λ₃/（λ₂＋λ₃）｝ｘ₃）

　よって、

λ₁ｆ（ｘ₁）＋λ₂ｆ（ｘ₂）＋λ₃ｆ（ｘ₃）

≧λ₁ｆ（ｘ₁）＋（λ₂＋λ₃）［ｆ（｛λ₂/（λ₂＋λ₃）｝ｘ₂＋｛λ₃/（λ₂＋λ₃）｝ｘ₃）］

≧ｆ（λ₁ｘ₁＋（λ₂＋λ₃）［｛λ₂/（λ₂＋λ₃）｝ｘ₂＋｛λ₃/（λ₂＋λ₃）｝ｘ₃］）

＝ｆ（λ₁ｘ₁＋λ₂ｘ₂＋λ₃ｘ₃）

　よって、ｎ＝３ のときも、Ｊｅｎｓｅｎ の不等式は成り立つ。

　同様な操作を行えば、全ての自然数 ｎ に対して、Ｊｅｎｓｅｎ の不等式が成り立つことが分
かる。
（詳しくは、数学的帰納法を用いて示される。）

　このＪｅｎｓｅｎ の不等式を用いると、相加平均と相乗平均の関係

　

は、次のように簡潔に証明される。

（証明）　区間 （０ ，∞） において、関数 ｆ（ｘ）＝−ｌｏｇ ｘ　は凸関数なので、

Ｊｅｎｓｅｎ の不等式より、

−（１/ｎ）ｌｏｇ ｘ₁−（１/ｎ）ｌｏｇ ｘ₂−・・・−（１/ｎ）ｌｏｇ ｘ_ｎ

≧−ｌｏｇ ｛（１/ｎ）ｘ₁＋（１/ｎ）ｘ₂＋・・・＋（１/ｎ）ｘ_ｎ｝＝−ｌｏｇ （ｘ₁＋ｘ₂＋・・・＋ｘ_ｎ）/ｎ

　よって、　ｌｏｇ （ｘ₁＋ｘ₂＋・・・＋ｘ_ｎ）/ｎ ≧ （１/ｎ）ｌｏｇ ｘ₁ｘ₂・・・ｘ_ｎ　が成り立ち、

　　　　　　　　　　　　

が示された。　　（証終）

　上記の証明は簡潔ではあるが、やはり技巧的な感じは拭えない。しばらく時間が経って、
この証明を復元するという自信が持てない。

　証明を復元するのに自信が持てない方のために、次のような直接的な証明を紹介してお
こう。（平成２２年３月２３日付け）

（別証）　関数 Ｆ（ｘ）＝ｌｏｇ ｘ　について、　Ｆ’（ｘ）＝１/ｘ　、Ｆ”（ｘ）＝−１/ｘ²＜０　より、関数

Ｆ（ｘ）＝ｌｏｇ ｘ　は上に凸である。

よって、　（ｘ₁＋ｘ₂＋・・・＋ｘ_ｎ）/ｎ＝ａ　とおくと、ｘ＝ａ　における接線の方程式は、

　ｙ＝１/ａ・（ｘ−ａ）＋ｌｏｇ ａ　なので、 １/ａ・（ｘ−ａ）＋ｌｏｇ ａ ≧ ｌｏｇ ｘ　が成り立つ。

このとき、ｋ＝１、２、３、・・・、ｎ に対して、

　１/ａ・（ｘ₁−ａ）＋ｌｏｇ ａ ≧ ｌｏｇ ｘ₁

　１/ａ・（ｘ₂−ａ）＋ｌｏｇ ａ ≧ ｌｏｇ ｘ₂

　１/ａ・（ｘ₃−ａ）＋ｌｏｇ ａ ≧ ｌｏｇ ｘ₃

　　・・・・・・・・・・・・・・・・・・・・・・・・

　１/ａ・（ｘ_ｎ−ａ）＋ｌｏｇ ａ ≧ ｌｏｇ ｘ_ｎ

　これらの ｎ 個の不等式を辺々加えて、

　ｎ・ｌｏｇ ａ ≧ ｌｏｇ ｘ₁＋ｌｏｇ ｘ₂＋ｌｏｇ ｘ₃＋・・・＋ｌｏｇ ｘ_ｎ

すなわち、　　 ｌｏｇ ａ ≧ （ｌｏｇ ｘ₁ｘ₂ｘ₃・・・ｘ_ｎ）/ｎ より、

　

が成り立つ。　（別証終）


　この相加平均と相乗平均の関係について、横浜市立大学（国際総合科学部　理系）の平
成１９年度入試問題は、ある意味斬新で面白いと思う。

次の問いに答えよ。

（１）　すべての実数 ｘ に対して、不等式　ｘ ≦ ｅ^ｘ-1　が成り立つことを示せ。

（２）　正の数 ｘ₁、ｘ₂、・・・、ｘ_ｎ　が、ｘ₁＋ｘ₂＋・・・＋ｘ_ｎ＝ｎ　を満たすとき、　ｘ₁ｘ₂・・・ｘ_ｎ≦１

　が成り立つことを示せ。

（３）　正の数 ａ₁、ａ₂、・・・、ａ_ｎ　に対して、　Ａ＝（ａ₁＋ａ₂＋・・・＋ａ_ｎ）/ｎ　とするとき、

　　ａ₁ａ₂・・・ａ_ｎ≦Ａ^ｎ

　が成り立つことを示せ。

（３）は正しく、相加平均と相乗平均の関係

　

の証明をせよという問題である。

（解）（１）　Ｆ（ｘ）＝ｅ^ｘ-1−ｘ　とおくと、　Ｆ’（ｘ）＝ｅ^ｘ-1−１　で、　Ｆ’（ｘ）＝０　より、　ｘ＝１

　ｘ＜１　で　Ｆ’（ｘ）＜０　、ｘ＞１　で　Ｆ’（ｘ）＞０　なので、Ｆ（ｘ）は、ｘ＝１　で極小かつ最小。

よって、　Ｆ（ｘ）≧Ｆ（１）＝０　より、　ｅ^ｘ-1−ｘ≧０　すなわち　ｘ≦ｅ^ｘ-1　が成り立つ。

（２）　（１）より、　ｘ₁ｘ₂・・・ｘ_ｎ≦ｅ^ｘ₁-1ｅ^ｘ₂-1・・・ｅ^ｘ_ｎ-1＝ｅ^{ｘ₁＋ｘ₂＋・・・＋ｘ_ｎ-ｎ}＝ｅ⁰＝１

（３）　ａ₁/Ａ＋ａ₂/Ａ＋・・・＋ａ_ｎ/Ａ＝ｎ　なので、（２）より、

　（ａ₁/Ａ）（ａ₂/Ａ）・・・（ａ_ｎ/Ａ）≦１　すなわち、　ａ₁ａ₂・・・ａ_ｎ≦Ａ^ｎ　が成り立つ。　　（終）


（コメント）　代数的な証明よりも、やはり解析的な証明の方が分かり易いですね！

　この不等式を用いて、次の問題が鮮やかに解かれる。

問　題　　６次方程式　ｘ⁶−６ｘ⁵＋ａｘ⁴＋ｂｘ³＋ｃｘ²＋ｄｘ＋１＝０　の解がすべて正であると
　　　　　き、定数 ａ、ｂ、ｃ、ｄ の値を求めよ。

　一見すると、「途方に暮れそうな．．．」問題であるが、不等式が等式の問題を解決するの
に役立つことを知ると、感動的ですらある。

（解）　６次方程式の解を、　ｘ_ｋ　（ｋ＝１，２，３，４，５，６）　とすると、

　相加平均と相乗平均の関係から、

　

ここで、解と係数の関係から、　左辺＝ｘ₁＋ｘ₂＋ｘ₃＋ｘ₄＋ｘ₅＋ｘ₆＝６　で、

ｘ₁・ｘ₂・ｘ₃・ｘ₄・ｘ₅・ｘ₆＝１　より、右辺＝６　で、左辺＝右辺　となり、等号が成立する。

よって、このとき、　ｘ₁＝ｘ₂＝ｘ₃＝ｘ₄＝ｘ₅＝ｘ₆＝１　となり、６次方程式の左辺は、

　（ｘ−１）⁶＝ｘ⁶−６ｘ⁵＋１５ｘ⁴ー２０ｘ³＋１５ｘ²−６ｘ＋１

よって、　ａ＝１５　、ｂ＝−２０　、ｃ＝１５　、ｄ＝−６　である。　　（終）


（コメント）　最初、本当にどうしようと思いました。こんな解法があるなんて、やはり数学は
　　　　　　面白いですね！


　当ＨＰ読者のＨＮ「red.pine.another」さんからのコメントです。（平成２４年１２月２７日付け）

　上記の問題で、６次方程式の係数を相加相乗平均を利用して解いているのですが、友人
と検討していて疑問が浮かびました。

　６つの解を相加相乗の式に当てはめて、等号成立条件より、　(ｘ−１)⁶＝０　としているの
ですが、これは解が自然数という縛りがなければ答えが定まらないのではないでしょうか？
また、等号が成り立つ必要もなく、解と係数の関係を満たせば答えが導かれるのではない
でしょうか？たとえば、(ｘ−２)²・(ｘ−１/２)⁴＝０　であれば、解は全て正で、解と係数の関
係も満たします。


（コメント）　６次方程式において、５次の係数が−６、定数項が１という条件が、この問題に
　　　　　　おいては決定的な条件で、解が自然数という条件がなくても自然数が解となり、し
　　　　　　かも他の係数も無条件に定まるというところが、この問題のユニークなところです。

　上記の解をもう少し補足したいと思います。

　相加平均と相乗平均の関係　　において、
ｘ_ｋ＞０　（ｋ＝１〜６）なので、等号が成り立つのは、ｘ₁＝ｘ₂＝ｘ₃＝ｘ₄＝ｘ₅＝ｘ₆　の場合に
限ります。

　しかも、解と係数の関係から、　ｘ₁＋ｘ₂＋ｘ₃＋ｘ₄＋ｘ₅＋ｘ₆＝６、ｘ₁・ｘ₂・ｘ₃・ｘ₄・ｘ₅・ｘ₆＝１

なので、等号が成立しています。したがって、ｘ₁＋ｘ₂＋ｘ₃＋ｘ₄＋ｘ₅＋ｘ₆＝６　より、

　ｘ₁＝ｘ₂＝ｘ₃＝ｘ₄＝ｘ₅＝ｘ₆＝１

とならざるを得ません。このとき、

ｘ⁶−６ｘ⁵＋ａｘ⁴＋ｂｘ³＋ｃｘ²＋ｄｘ＋１＝（ｘ−１）⁶
＝ｘ⁶−６ｘ⁵＋１５ｘ⁴ー２０ｘ³＋１５ｘ²−６ｘ＋１

から、　ａ＝１５　、ｂ＝−２０　、ｃ＝１５　、ｄ＝−６　と定まり、これ以外はあり得ません。


※　red.pine.another さんが例示された (ｘ−２)²・(ｘ−１/２)⁴　は定数項が１となり得ず、問
　題に合致しません。


　読者のために、練習問題を残しておこう。

練習問題　　３次方程式　ｘ³−３ｘ²＋ａｘ−１＝０　の解がすべて正であるとき、定数 ａ の
　　　　　　　値を求めよ。

　答えは、もちろん、　３　である。


　当ＨＰの読者の方からの質問です。（平成２３年８月３日付け）

　相加相乗平均の関係についての質問です。相加平均と相乗平均の関係の証明は５０くら
いはある、ということを聞いたことがあります。ただ、ネットや参考書などで一生懸命探して
も、なかなか見つかりませんでした。

［質問の内容］

　相加相乗平均の関係の一般の場合についての証明を考えていた時のことです。

　これまでに微分して解析的に示す方法や、２^k の場合を示してさかのぼる帰納法、

「ａ₁≦ａ₂、ｂ₁≦ｂ₂ について、ａ₁ｂ₂＋ａ₂ｂ₁≦ａ₁ｂ₁＋ａ₂ｂ₂ 」を帰納的に利用する方法など、

いくつかの証明を見てきました。理解は容易なものの、なんだか煙に巻かれたようなしっくり

こない心地でいました。

そこで、相加相乗平均の関係（を少しだけ書き換えたもの）

　ｎ（ｂ₁ｂ₂・・・ｂ_ｎ）≦ｂ₁^ｎ＋ｂ₂^ｎ＋・・・＋ｂ_ｎ^ｎ

を眺めていたところ、

　ｎ（ｂ₁ｂ₂・・・ｂ_ｎ）＝ｂ₁ｂ₂・・・ｂ_ｎ＋ｂ₁ｂ₂・・・ｂ_ｎ＋・・・＋ｂ₁ｂ₂・・・ｂ_ｎ　（ｎ 個の和）

と考えると、ｂ₁、ｂ₂、・・・、ｂ_ｎ を、ｎ個ずつ用意して合計ｎ²個の元を、ｎ個ずつの組に分け、

組の中で積を作って、それらを足したものの大小の関係であることに気付きました。

　ｂ_1≦ｂ₂≦・・・≦ｂ_ｎ と順序をつけてよく、このとき、左辺では組として、(ｂ₁，ｂ₂，・・・，ｂ_ｎ)

がｎ組という、大小が入り乱れた組を作っており、右辺では、

　(ｂ₁，ｂ₁，・・・，ｂ₁)、(ｂ₂，ｂ₂，・・・，ｂ₂)、・・・、(ｂ_ｎ，ｂ_ｎ，・・・，ｂ_ｎ)

という、大きいものは大きいもの同士で組を作る、という風になっています。

　これらに示したい大小関係がつくのは明らかに思えます。つまり、示したいことが、次の事
柄になったのです。

　ｍｎ個の非負の元からなる(広義)単調増加な数列　ａ₁，ａ₂，・・・，ａ_ｍｎ　について、

この数列を任意に並び換えたものを、　ｂ₁，ｂ₂，・・・，ｂ_ｍｎ　とすると、

ａ₁ａ₂・・・ａ_ｎ＋ａ_ｎ+1ａ_ｎ+2・・・ａ_ｎ+ｎ＋・・・＋ａ_(ｍ-1)ｎ+1ａ_(ｍ-1)ｎ+2・・・ａ_ｍｎ

≧ ｂ₁ｂ₂・・・ｂ_ｎ＋ｂ_ｎ+1ｂ_ｎ+2・・・ｂ_ｎ+ｎ＋・・・＋ｂ_(ｍ-1)ｎ+1ｂ_(ｍ-1)ｎ+2・・・ｂ_ｍｎ　・・・（★）

　しかし、いざ示してみようとすると、そこまで単純なものではないのか、かなり苦戦しました。
いろいろ調べていたところ、「並べかえ不等式」と関係していそうだと思い、まずこれを一般
化することから始めました。

　なんとかその証明も自分なりに完成し、正しいかどうかはわかりませんが、そこから（★）も
解決することができました。

　そこで、質問です。：　（★）という命題を容易に証明することは可能でしょうか。


　上記と同じ方からの質問です。（平成２３年８月２０日付け）

　前回、ｍｎ個の元からｎ個ずつ取り出し、積をとったものを順次足す、ということを質問しま
したが、これを直接的に証明することができました。また、並べかえ不等式についても、証
明をある程度丁寧に書いてみました。（→　ｐｄｆ１　、　ｐｄｆ２）

　さて、この並べかえ不等式は、いわば積和の関係式ですが、それと双対（？）の関係とい
うのでしょうか、和と積の役割を完全に入れ替えた、和積の不等式も全く同様の方法が適
用されることに気がつきました。

　置換を施す前後の積和の差は、

　(A₁A₂＋B₁B₂)−(A₁B₂＋B₁A₂)＝(A₁−B₁)(A₂−B₂)

という因数分解が成立しましたが、和積の場合は、

(A₁＋A₂)(B₁＋B₂)−(A₁＋B₂)(A₂＋B₁)＝(A₁B₂＋B₁A₂)−(A₁A₂＋B₁B₂)＝(A₁−B₁)(B₂−A₂)

という因数分解ができます。このことから、積和に関する並べ替えの不等式を和積になおす
と、（証明はひとえにこの因数分解によっているので）不等号が正反対になりました。その点
を除けば、証明はほぼ同じものでした。

　これは、和が一定の場合、いくつかの積をできる限り大きくするには、全部が等しくなるよ
うにすればよいことに関係していそうです。これはまだpdfにまとめることはできていません。

　また、その和積の場合の不等式も、相加相乗平均の関係の証明となっていました。

　｛(a₁+a₂+・・・+a_n)/n｝^ｎ とは、a₁/n、a₂/n、・・・、a_n/n を n 個ずつ用意した場合のひとつの
和積であり、大きいものは大きいもの同士、小さいものは小さいもの同士で足して積を作っ
たほうが小さくなり、そう並べかえると、

　（a₁/n＋・・・＋a₁/n）（a₂/n＋・・・＋a₂/n）・・・（a_ｎ/n＋・・・＋a_ｎ/n）＝a₁a₂・・・a_n

なので、｛(a₁＋a₂＋・・・＋a_n)/n｝^ｎ≧a₁a₂・・・a_n　より、ｎ乗根をとると、

　(a₁＋a₂＋・・・＋a_n)/n≧（a₁a₂・・・a_n）^1/n

となります。相加相乗平均は、和の平均と積の平均の関係なので、これは当たり前のこと
なのかもしれません。ここまでが、今確かに得ていることです。

　さらに、積和に関する並べかえの不等式から、チェビシェフの和の不等式が導かれること
は有名です。
（ウィキペディアに、その方法による証明がありました。（→　「チェビシェフの和の不等式」）

　チェビシェフの不等式の双対（？）にあたる不等式を考えてみようと思ったのです。すると、
（もしかすると有名なことなのかもしれませんが・・・）それはコーシー・シュワルツの不等式
の一般形になっていると言えそうだと気づきました。

　チェビシェフの不等式における　(a₁＋a₂＋・・・＋a_n)/n・(ｂ₁＋ｂ₂＋・・・＋ｂ_n)/n　について、
和を積に、積を和に、1/nを1/n乗（n乗根）に変えてみると、

　(a₁a₂・・・a_n)^1/n＋(ｂ₁ｂ₂・・・ｂ_n)^1/n

となります。また、同様に、　(a₁b₁＋a₂b₂＋・・・＋a_nb_n)/n　を書き換えると、

　｛(a₁＋b₁)(a₂＋b₂)・・・(a_n＋b_n)｝^1/n

となります。

　ここで、　a_i、b_i を a_iⁿ、b_iⁿ で置き換え、全体をそれぞれ ｎ 乗することで、

（a₁a₂・・・a_n＋ｂ₁ｂ₂・・・ｂ_n）^ｎ≦(a₁^ｎ＋b₁^ｎ)(a₂^ｎ＋b₂^ｎ)・・・(a_n^ｎ＋b_n^ｎ)

が得られました。これは、２次元のn個のベクトルのコーシー・シュワルツの不等式であるは
ずです。

　チェビシェフの不等式において、数列の数を増やしていいように、これも２次元の場合が
示されれば、ｋ次元でも帰納的に示されるので、２次元を証明することが重要だと考えまし
た。

　そこで、チェビシェフの不等式の証明を、そっくりそのまま積と和を入れ替えて適用しよう
と試みましたが、これはどうもうまくいきません・・・。チェビシェフの不等式の場合、和積を
展開し、ｎ個の積和とみなして評価しています。しかし、コーシーシュワルツになると、最初
は積和の状態で、展開できないため、n個の何がしか、という解釈ができずに困りました。
この並べ替えの考え方を用いて、どうにかコーシー・シュワルツの不等式の拡張した場合
を示せないものでしょうか。

　相加相乗平均の関係をうまく使う方法や、相加相乗平均の逆戻りする帰納法に類似した
方法による証明は理解できたのですが、どうにか、この並べ替えの考え方で証明したいな、
と思っています。何かいい方法はないでしょうか。


（追記）　令和６年９月５日付け

　相加平均と相乗平均の関係として、

　ａ≧０ 、ｂ≧０ に対して、

　

は、よく知られた不等式である。これを、

　（１/２）ａ＋（１/２）ｂ≧ａ＾(1/2)・ｂ＾(1/2)

と変形してみると、一般化の道筋が見えてくる。

　非負の数 ａ、ｂ に対して、

　λａ＋μｂ≧ａ＾λ・ｂ＾μ　（λ、μは正の数で、λ＋μ＝１）

が成り立つ。等号成立は、ａ＝ｂ のときに限る。

　これは、重み付き相加相乗平均の関係と言われる。

　この証明には、Jensen の不等式を用いるのが最も美しいと言われる。

（証明）　区間 （０ ，∞） において、関数 Ｆ（ｘ）＝−ｌｏｇ ｘ　は凸関数なので、Jensen の不等式

から、　λＦ（ａ）＋μＦ（ｂ）≧Ｆ（λａ＋μｂ）　が成り立つ。等号成立は、ａ＝ｂ　に限る。

　すなわち、　−λｌｏｇ ａ−μｌｏｇ ｂ≧−ｌｏｇ （λａ＋μｂ）　より、

ｌｏｇ ａ＾λ・ｂ＾μ≦ｌｏｇ （λａ＋μｂ）　なので、λａ＋μｂ≧ａ＾λ・ｂ＾μ　が成り立つ。　　（証終）


　令和６年８月１６日付け朝日新聞朝刊に、「数学は世界をつなぐ共通の言語」と題して、特
集が掲載された。自由な発想と創造力で世界とつながるべく、挑戦してみた。

問題　　実数 ａ、ｂ が、ａ≧ｂ＞０　、ａ＋ｂ＝１　を満たすとき、　（ａ＋２ｂ）（ａ＾ａ）（ｂ＾ｂ）＜１
　　が成り立つことを示せ。

＃国際数学オリンピック問題を改題

（解）　重み付き相加相乗平均の関係から、　（ａ＾ａ）（ｂ＾ｂ）≦ａ²＋ｂ²　が成り立つので、

　（ａ＋２ｂ）（ａ＾ａ）（ｂ＾ｂ）≦（ａ＋２ｂ）（ａ²＋ｂ²）

ａ≧ｂ＞０　なので、

（ａ＋２ｂ）（ａ²＋ｂ²）＝（ａ＋２ｂ）ａ²＋（ａ＋２ｂ）ｂ²

ここで、　ａ＋３ｂ−（ａ＋２ｂ）＝ｂ＞０　より、　ａ＋２ｂ＜ａ＋３ｂ

　３ａ＋ｂ−（ａ＋２ｂ）＝２ａ−ｂ＝ａ＋（ａ−ｂ）＞０　より、　ａ＋２ｂ＜３ａ＋ｂ

なので、　（ａ＋２ｂ）（ａ²＋ｂ²）＜（ａ＋３ｂ）ａ²＋（３ａ＋ｂ）ｂ²＝（ａ＋ｂ）³

ａ＋ｂ＝１　なので、　（ａ＋２ｂ）（ａ²＋ｂ²）＜１

したがって、　（ａ＋２ｂ）（ａ＾ａ）（ｂ＾ｂ）＜１　が成り立つ。　　（終）



　　以下、工事中