凸図形の基礎知識 
三角形、長方形、円、直方体、円柱、円錐、球、・・・など世の中には様々な凸図形が存在
する。





これらに共通する性質は、「凹(へこ)んでいない」という点だろう。この性質を、数学的に
記述すれば、
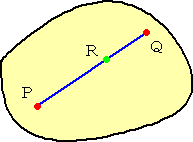
図形上の任意の2点を結ぶ線分上の点はまた図形上の点である
すなわち、原点を始点とする点Pの位置ベクトルを、P と書くとき、
『 図形 K 上の任意の2点 P と Q に対して、
R=sP+tQ ( s+t=1 、s≧0 、t≧0 )
で定まる点 R もまた図形 K 上の点である 』
ということである。
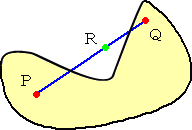
したがって、 次のような場合は、凸図形とは言わない。
凸図形の例 上記であげたもの以外に次の図形も凸図形である。
(1) 直線、半直線、線分、点
(2) 中心角がπ以下の扇形
(3) 平面、半平面
これ以外にも、たくさん凸図形は存在する。
凸図形の定義から、次の事実が成り立つことは明らかだろう。
凸図形 K が同一直線上にない3点A、B、Cを含めば、△ABCはKに含まれる
したがって、
同一直線上にない3点A、B、Cを含む最小の凸図形は、△ABCである
ことが言える。

いま、2つの図形 K と H の交わりの図形を、 K∩H と表すことにする。
このとき、次の事実が成り立つ。
2つの図形 K と H が凸図形ならば、その交わり K∩H も凸図形である
(証明) K∩H≠φ とする。 K∩H が1点だけからなる場合は、明らかに凸図形。
K∩H の任意の異なる2点を P と Q とする。
このとき、K 、H は凸図形なので、 線分PQは、K 、H に含まれる。
よって、 線分PQは、K∩H に含まれるので、 K∩H は凸図形である。 (証終)
次の事実が成り立つことも明らかだろう。
凸図形の内部の点から引いた半直線は、凸図形の境界とただ1点で交わる
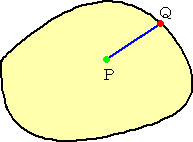
半直線は凸図形なので、凸図形との交わりは凸図形。線分PQの両端を除いて線分上
の点は全て凸図形の内部の点である。よって、半直線と凸図形の境界との交点は点Qの
みである。
上図で、点Pの周りに点Qが境界上を動くとき、点Qには2つの向きが可能である。
反時計回りに動くとき、 正の巡回
時計回りに動くとき、 負の巡回
と名付ける。
さらに、直線は平面を2つの半平面(凸図形)に分けるので、
凸図形と直線が交わるとき、凸図形は2つの凸図形に分割される
ことも明らかだろう。
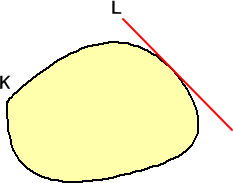
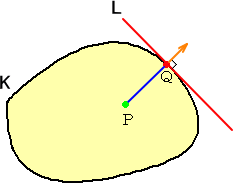
右図のように、凸図形 K に対して、
K の境界と共有点を持つが、
K の内部の点とは共有点を持たない
ような直線 L のことを、
凸図形 K の 支持直線
という。 |
 |
(支持直線というのは、いわゆる「接線」というイメージで理解していいのだろうか?)
この点に関して、HN「takahiro」さんからのコメントです。(平成29年7月13日付け)
支持直線は境界線が連続であればいいのに対して、接線は境界線が微分可能である必
要があります。
(コメント) 支持直線の方が広い意味なんですね!takahiro さんに感謝します。
凸図形の境界の点に「向き」が考えられたように支持直線についても「向き」が考えられる。
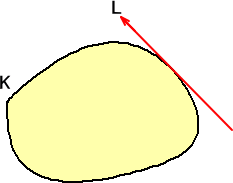
支持直線 L の正の向きを、
凸図形 K が、支持直線 L の左側にあるような向き
と定める。即ち、下図の向きが、支持直線 L の正の向きである。
多角形のうち、凸図形の性質を持つものを、凸多角形という。
凸多角形 K とその境界上の点 P を通る支持直線 L について、点 P が境界上で正の
巡回に1周すれば、支持直線 L は反時計回りに360度回転する。
(このことは、一般の凸図形についても成り立つ性質だろう。)
有界な凸図形 K に対して、内接する凸多角形や外接する凸多角形が定義される。
内接する凸多角形 ・・・ 境界上の幾つかの点を正の巡回の向きに線分で結んで得られ
る図形
外接する凸多角形 ・・・ 全ての辺が凸図形 K の支持直線の一部である図形
(コメント) 今まで三角形の頂点に名前を付けるとき、反時計回りに付けることが多かっ
た。これは、まさに凸図形の正の巡回の向きと一致する。これまで、「人間は右
利きが多い。右利きの人が一番書きやすい向きが反時計回りだよ!」と、思っ
ていたが、実は違うんですね!
今までは、凸図形として、平面上の図形をイメージしてきたが、もちろん、3次元空間にお
ける凸図形も考えられる。
3次元空間における凸図形のことを、凸体という。
凸図形の定義から、次の事実が成り立つことは明らかだろう。
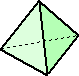
凸体 K が同一平面上にない4点A、B、C、Dを含めば、四面体A-BCDはKに含
まれる
したがって、
同一平面上にない4点A、B、C、Dを含む最小の凸体は、四面体A-BCDである
ことが言える。
また、次の事実が成り立つ。
2つの図形 K と H が凸体ならば、その交わり K∩H も凸図形である
交わりが1点だったり、線分だったり、面だったり、凸体だったり、様々の可能性があるだ
ろう。
次の事実が成り立つことも明らかだろう。
凸体の内部の点から引いた半直線は、凸体の境界とただ1点で交わる

半直線は凸図形なので、凸図形との交わりは凸図形。線分PQの両端を除いて線分上
の点は全て凸体の内部の点である。よって、半直線と凸体の境界との交点は点Qのみで
ある。
右図のように、凸体 K に対して、
K の境界と共有点を持つが、
K の内部の点とは共有点を持たない
ような平面 L のことを、
凸体 K の 支持平面
という。 |
 |
(球の支持平面は、その接平面なので、何となくイメージできるかな?)
このとき、次の事実が成り立つは明らかだろう。
凸体の内部の点から引いた半直線に対して、この半直線に垂直な支持平面がただ
一つ存在する
左図のように、凸体 K の境界上の点Qを通る支持平
面 L に垂直で、外側に向かうベクトルを、点Qにおける
外法線という。
平面上における「角」の役割を、3次元空間では、凸錐が果たす。
凸錐とは、1点から無数に出る半直線からなる非有界な凸体のことをいう。
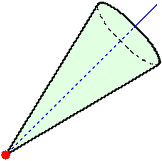
上図では円錐を用いたが、凸多角錐や、なす角がπより小の2平面で挟まれる凸体なども
凸錐の例になる。
球の表面上に2点A,Bがあり、これらは直径の両端ではないものとする。このとき、2点
A,Bを通る大円がただ1つ存在する。2つできる弧のうち、小さい方を通常考え、これを、2
点A,Bを結ぶ球面弧という。
直径の両端を含まず、任意の2点を結ぶ球面弧も含む球面上の図形を、球面上の凸図
形という。
上記の円錐と球面が交わるとき、その交わりは、球面上の凸図形となる。
また、球面上の凸 n 角形は、n 個の大円で囲まれる球面上の凸図形である。
(n=3 のときは、球面三角形となる。)
凸図形の支持直線(平面)を用いて、凸図形の幅が定義される。
凸図形 K に対して、直線 L に垂直な2つの支持直線(平面)の間の距離を、
直線 L に沿う方向の幅
という。このとき、幅が最大になる場合と最小になる場合がある。
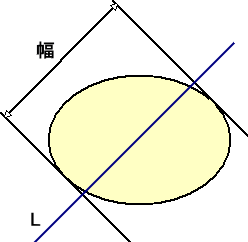
例 円は、どの方向においても幅が一定である。(定幅曲線 → 参考: 正方形を彫る )
例 楕円では、長軸方向が最大幅を与え、短軸方向が最小幅を与える。
次の事実が成り立つことは明らかだろう。
凸図形上の2点間の距離の最大値(直径という)は、最大幅に等しい
例 円の最大幅は、円の直径に等しい。
平行な支持直線間の距離が常に一定である凸図形は、定幅曲線と言われる。上記の例
からも明らかなように、円は定幅曲線の最も簡単な例である。
円とは異なる定幅曲線では次の例が有名だろう。
例 1辺がaの正三角形において、各頂点で半径aの円弧を描く。
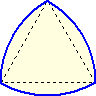
(証明) 互いに平行な2本の支持直線をどのように引いても、1つは必ず正三角形の頂点
を通り、他方は、円弧の接線となるので、その距離は常に一定である。 (証終)
以下、工事中


















