椬傝崌偆暘悢丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂惍悢偺悽奅偱偼丄俀 偲 俁 偼乽椬傝崌偭偰偄傞乿丄俁 偲 俆 偼乽椬傝崌偭偰偄側偄乿偩傠偆偲偄偆
偙偲偼捈姶揑偵棟夝偱偒傞丅
丂惍悢榑偱丄乽楢懕偡傞俁惍悢偺愊偼丄俇 偺攞悢偱偁傞乿偲偄偆掕棟偑偁傞偑丄偙傟偼惓妋偵
偼乽椬傝崌偆俁偮偺惍悢偺愊偼丄俇 偺攞悢偱偁傞丅乿偲偡傋偒偩傠偆丅
丂偲偙傠偑丄暘悢偺悽奅偵悢偺斖埻傪奼偘偨応崌丄乽椬傝崌偆乿偲偄偆姶妎偑晄柧妋偵側傞丅
丂椺偊偽丄
丂丂暘悢偺 侾/俁 偲 侾/俀 偼丄壥偨偟偰椬傝崌偭偰偄傞偺偩傠偆偐丠
丂丂暘悢偺 侾/俁 偲 俀/俁 偼丄偳偆側傫偩傠偆偐丠
丂丂丂丂丂丏丏丏丏丏丏丏丏丏丂媈栤偼恠偒側偄丅
丂偙偺栤戣偵懳偟偰丄師偺傛偆側峫偊曽偑偁傞偙偲傪嵟嬤抦偭偨丅
掕媊丂丂俀偮偺暘悢 倎/倐 丄們/倓 乮倎丆倐丆們丆倓 偼惍悢偱丄倐丆倓亜侽乯偵懳偟偰丄
丂丂倎倓亅倐們亖亇侾
偑惉傝棫偮偲偒丄俀偮偺暘悢 倎/倐 丄們/倓 偼椬傝崌偆偲偄偆丅
丂倐亖倓亖侾丂偡側傢偪丂俀偮偺悢偑丄偲傕偵惍悢偺応崌偼丄変乆偺崱傑偱偺捈姶揑棟夝偲
堦抳偡傞丅
丂偙偺掕媊傪梡偄傞偲丄侾/俁 偲 侾/俀 偼丄椬傝崌偭偰偄傞偲尵偊傞偑丄侾/俁 偲 俀/俁 偼丄椬傝
崌偭偰偄傞偲偼尵偊側偄偙偲偵側傞丅
丂侾/俀 偲 俀/俁 偵偮偄偰偼丄侾/俁亙侾/俀亙俀/俁 側偺偱丄乽偁乣偦偆偐側乣乿偲偄偆姶偠側偺偩
偑丄侾/俁亙俋/俀侽亙侾/俀 偱偁傞 俋/俀侽 偑 侾/俁 偲偼椬傝崌偭偰偄側偄偙偲傪巚偆偲丄偲偰傕
晄巚媍側姶妎偩偲偄偊傞丅
丂壓恾偵丄暘悢傪暲傋偰傒偨丅
丂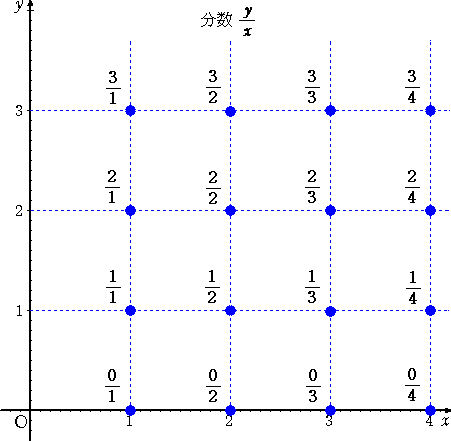
丂暘悢慡懱偑丄壛嶼廤崌傪帵偡偵偼忋恾偱廫暘偱偁傞偑丄乽椬傝崌偆乿偲偄偆姶妎傪愢柧偡
傞偵偼晄廫暘偱偁傞丅
| 丂掕媊偵傛傟偽丄俀偮偺楍儀僋僩儖 |
丂 |
丂偵傛偭偰惗惉偝傟傞暯峴巐曈宍偺柺愊 |
| 偑 侾 偱偁傞偲偒偵丄俀偮偺暘悢偼乽椬傝崌偆乿偙偲偵側傞丅 |
丂偙偺偙偲傪尵偄姺偊傟偽丄柺愊 侾 偺惓曽宍偵堦師曄姺傪巤偟偰丄柺愊偑晄曄側応崌丄偦
偺侾師曄姺傪昞偡峴楍偺楍儀僋僩儖偼丄椬傝崌偆暘悢傪惗惉偡傞偙偲偵側傞丅
丂乮傕偪傠傫丄峴楍偺惉暘偼慡偰惍悢偲偡傞丅乯
丂椬傝崌偆暘悢偵偼丄師偺傛偆側柺敀偄惈幙傕偁傞傜偟偄丅
惈幙乮侾乯丂俀偮偺暘悢 倎/倐 丄們/倓 乮倎丆倐丆們丆倓 偼惍悢偱丄倐丆倓亜侽乯偑椬傝崌偆暘悢
丂丂丂丂丂偱偁傞偲偒丄俀偮偺暘悢偼婛栺暘悢偱側偗傟偽側傜側偄丅
乮徹柧乯丂暘悢 倎/倐 偑婛栺暘悢偱側偄偲壖掕偡傞偲丄嵟戝岞栺悢 乮倎丆倐乯偼侾偲偼堎側傞丅
丂忦審傛傝丄倎倓亅倐們亖亇侾 偱丄嵍曈偑 乮倎丆倐乯 偱妱傝愗傟傞偙偲偵側傝丄柕弬丅
丂傛偭偰丄暘悢 倎/倐 偼婛栺暘悢丅暘悢 們/倓 偵偮偄偰傕摨條偱偁傞丅丂丂乮徹廔乯
惈幙乮俀乯丂俀偮偺暘悢 倎/倐 丄們/倓 乮倎丆倐丆們丆倓 偼惍悢偱丄倐丆倓亜侽乯偑椬傝崌偆暘悢
丂丂丂丂丂偱偁傞偲偒丄暘悢 乮倎亄們乯/乮倐亄倓乯 偼丄偙傟傜偺娫偵偁偭偰丄椉曽偵椬傝崌偆
丂丂丂丂丂暘悢偲側傞丅
乮徹柧乯丂俀偮偺暘悢 倎/倐 丄們/倓 偼椬傝崌偆暘悢偱偁傞偺偱丄倎倓亅倐們亖亇侾
丂乮倎亄們乯/乮倐亄倓乯 偲 倎/倐 偵偮偄偰丄乮倎亄們乯倐亅乮倐亄倓乯倎亖倐們亅倎倓亖亇侾丂側偺偱丄
丂暘悢 乮倎亄們乯/乮倐亄倓乯 偲 倎/倐 偼椬傝崌偆暘悢偱偁傞丅
摨條偵偟偰丄
丂乮倎亄們乯/乮倐亄倓乯 偲 們/倓 偵偮偄偰丄乮倎亄們乯倓亅乮倐亄倓乯們亖倎倓亅倐們亖亇侾丂側偺偱丄
丂暘悢 乮倎亄們乯/乮倐亄倓乯 偲 們/倓 偼椬傝崌偆暘悢偱偁傞丅
傑偨丄乮乮倎亄們乯/乮倐亄倓乯亅倎/倐)(乮倎亄們乯/乮倐亄倓乯亅們/倓乯亖亅侾/倐2乮倐亄倓乯2亙侽
傛傝丄乮倎亄們乯/乮倐亄倓乯 偼丄俀偮偺暘悢 倎/倐 丄們/倓 偺娫偵偁傞丅乮徹廔乯
丂偙偺惈幙乮俀乯偐傜丄侾/俁 偲 侾/俀 偼丄椬傝崌偆暘悢側偺偱丄
丂侾/俁亙俁/俉亙俀/俆亙俁/俈亙侾/俀
偲師乆偵椬傝崌偆暘悢偑偱偒傞偐偵傒偊傞偑丄偦傟偼丄椬傝崌偆嶰幰娫偺娭學偱偁偭偰丄
棧傟偨悢摨巑偼丄傗偼傝椬傝崌傢側偄傕偺
丂忋偺応崌偩偲丄侾/俁 偲 俁/俈丆俁/俉 偲 俁/俈丆丒丒丒
傕弌偰偔傞丅側傫偐廂廍偑偮偐側偄姶偠偩丅
丂偙偺乽椬傝崌偆暘悢乿偲偄偆奣擮偐傜丄偳偺傛偆側悢妛偑揥奐偝傟傞偺偐丄偲偰傕嫽枴偑偁傞丅
乮嶲峫暥專丗俬丏俵丏僎儖僼傽儞僩丂俙丏僔儏儞丂挊丂晉塱丂惎丂愒旜榓抝丂栿
丂丂丂丂丂丂丂丂僎儖僼傽儞僩愭惗偺妛峑偵峴偐偢偵傢偐傞悢妛丂俁丂戙悢乮娾攇彂揦乯乯
乮捛婰乯丂暯惉侾俋擭俆寧侾俋擔晅偗
丂暯惉侾俋擭俆寧俉擔晅偗偱丄摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵丄俫俶乽悢妛偼偲偙偲傫擄偟偄乿
偝傫偐傜彂偒崬傒偑偁偭偨丅
丂丂僥儗價斣慻傪傒偰偄傞偲丄偳偆傕乽梊崘仺杮曇乿偺楢嵔傪媞娤揑側暥懱偱愰揱僐乕僪傪梫
丂強梫強偵杽傔崬傫偱偄傞偲傒傜傟丄偙傟傜傪扵媮偟偰偄偔偲丄堦擭娫傪侾俀嬫夋偵暘妱偱偒丄
丂乽6丂5/6丂5丂4/5丂4丂3/4丂3丂2/3丂2丂1/2丂1丂0/1丂0乿(0偼6偵傑偨6偼0偵抲偒姺偊丄悢楍
丂偺椫偱峫偊傞)偺僥乕儅偱悢楍傪峔惉偟偰偄傞暤埻婥偱偁傞丅摿偵暘悢偺暲傃偑柇側偺偱
丂僀儞僞乕僱僢僩専嶕傪偡傞偲乽僼傽儗僀悢楍乿乽婛栺暘悢乿乽僗僞乕儞亖僽儘僐僢僩栘乿傪妱傝弌
丂偟偨偑丄偙傟埲忋偺帒椏偼尒摉偨傜側偄丅偙傟傜偺悢楍偼壗傪堄枴偟偰偄傞偺偩傠偆偐丅
丂乽椬傝崌偆暘悢乿偲偄偆儁乕僕偼暯惉侾俆擭俇寧崰傾僢僾偟偨傕偺偱丄忢乆乽椬傝崌偆暘悢乿傗丄
暘悢偺崌棟揑側斣崋偺晅偗曽傪偳偆偡傞偐側偳摢偺曅嬿偵偁偭偨丅宖帵斅偺彂偒崬傒傪
尒偰傎傏係擭傇傝偺尒捈偟傪偟傛偆偲巚偄棫偭偨丅
丂偲偙傠偱丄悢妛僙儈僫乕乮擔杮昡榑幮乯丂俀侽侽俆擭俀寧崋乣係寧崋偱丄嫗搒戝妛嫵庼偱偁傜
傟偨娾堜陰椙偝傫偑乽暘悢偺悽奅乿偲戣偟偰楢嵹偝傟偰偄傞丅傑偨丄悢妛僙儈僫乕丂俀侽侽俈擭
俁寧崋偱丄愺堜揘栫偝傫偑乽僄儗僈儞僩側夝摎傪傕偲傓乿偱椬傝崌偆暘悢傪榖戣偵偝傟偰偄傞丅
帪偼惓偵乽椬傝崌偆暘悢乿偱弉偟偨偐偺傛偆偱偁傞丅
仈娾堜陰椙偝傫偑俀侽俀侾擭俉寧俇擔偵惱嫀偝傟偨丅嬣傫偱垼搲偺堄傪昞偟傑偡丅
丂偄傑丄偙偺儁乕僕傪撉傒曉偟偰偄偰丄
惈幙乮俀乯丂俀偮偺暘悢 倎/倐 丄們/倓 乮倎丆倐丆們丆倓 偼惍悢偱丄倐丆倓亜侽乯偑椬傝崌偆暘悢
丂丂丂丂丂偱偁傞偲偒丄暘悢 乮倎亄們乯/乮倐亄倓乯 偼丄偙傟傜偺娫偵偁偭偰丄椉曽偵椬傝崌偆
丂丂丂丂丂暘悢偲側傞丅
偐傜嶌傜傟偨偱偁傠偆栤戣
丂倎丆倐丆們丆倓 偑惓偺悢偱丄 倎/倐 亙 們/倓 側傜偽丄
丂倎/倐 亙 乮倎亄們乯/乮倐亄倓乯 亙們/倓丂
偑惉傝棫偮偙偲傪徹柧偣傛丅
偑擼棤傪偐偡傔傞丅偙偺栤戣偼屆偔偼暉壀嫵堢戝妛偱弌戣偝傟偨傕偺偩偑丄嫵壢朤梡偺
栤戣廤偱夝偄偨妎偊偑偁傞曽偑傎偲傫偳偩傠偆丅
丂巹帺恎丄偙偺栤戣傪崅峑侾擭偺晄摍幃偺徹柧偺帪娫偵夝偄偨妎偊偑偁傞偑丄偙偺栤戣
偑乽椬傝崌偆暘悢乿偺榖戣偵娭學偟偰偄傞偲偼丄偦偺摉帪丄旝恛傕巚傢側偐偭偨両
丂帺慠悢 値 埲壓偺暘曣傪帩偮 侽 埲忋 侾 埲壓偺婛栺暘悢傪戝偒偝偺弴偵彫偝偄曽偐傜暲
傋偨悢楍傪丄僼傽儗僀乮俥倎倰倕倷乯悢楍偲偄偆丅僼傽儗僀悢楍傪丄俥値 偲昞偡偙偲偵偡傞丅
椺丂悢楍 俥1 偼丄 侽/侾丂丆丂侾/侾丂丂乮悢 侽 傪暘悢 侽/侾 偱昞偡丅乯
椺丂悢楍 俥2 偼丄 侽/侾丂丆丂侾/俀丂丆丂侾/侾
椺丂悢楍 俥3 偼丄 侽/侾丂丆丂侾/俁丂丆丂侾/俀丂丆丂俀/俁丂丆丂侾/侾
椺丂悢楍 俥係 偼丄 侽/侾丂丆丂侾/係丂丆丂侾/俁丂丆丂侾/俀丂丆丂俀/俁丂丆丂俁/係丂丆丂侾/侾
椺丂悢楍 俥俆 偼丄 侽/侾丂丆丂侾/俆丂丆丂侾/係丂丆丂侾/俁丂丆丂俀/俆丂丆丂侾/俀丂丆丂俁/俆丂丆丂俀/俁丂丆丂俁/係丂丆丂係/俆丂丆丂侾/侾
椺丂悢楍 俥俇 偼丄 侽/侾丂丆丂侾/俇丂丆丂侾/俆丂丆丂侾/係丂丆丂侾/俁丂丆丂俀/俆丂丆丂侾/俀丂丆丂俁/俆丂丆丂俀/俁丂丆丂俁/係丂丆丂係/俆丂丆丂俆/俇丂丆丂侾/侾
丂忋婰椺偺悢楍偵偍偄偰怴偟偄崁偑丄慜抜偺俀偮偺暘悢 倎/倐 丆們/倓 偐傜丄乮倎亄們乯/乮倐亄倓乯
偲偄偆宍偺拞娫暘悢偵傛傝梌偊傜傟偰偄傞揰偑柺敀偄丅姺尵偡傟偽丄椬傝崌偆暘悢偺榖戣
偵娭學偡傞偲偄偆偙偲偩丅
丂僼傽儗僀悢楍 俥値 偑丄偄偔偮偺崁偐傜側傞悢楍偐偲偄偆栤偄偵懳偟偰丄師偺帠幚偑抦傜傟
偰偄傞丅僼傽儗僀悢楍偺摿挜偐傜柧傜偐偩傠偆丅
丂僆僀儔乕偺娭悢 冇乮値乯丂偵懳偟偰丄僼傽儗僀悢楍 俥値 偺崁悢偼丄
丂侾亄冇乮侾乯亄冇乮俀乯亄丒丒丒亄冇乮値乯
偵傛傝梌偊傜傟傞丅
丂扐偟丄冇乮値乯亖乮1 偐傜 値 傑偱偺帺慠悢偺偆偪 値 偲屳偄偵慺側傕偺偺屄悢乯
椺丂冇乮侾乯亖侾丂丄冇乮俀乯亖侾丂丄丂冇乮俁乯亖俀丂丄冇乮係乯亖俀丂丄丒丒丒丂側偺偱丄
丂僼傽儗僀悢楍俥1 偺崁悢偼丄丂侾亄冇乮侾乯亖俀
丂僼傽儗僀悢楍俥2 偺崁悢偼丄丂侾亄冇乮侾乯亄冇乮俀乯亖俁
丂僼傽儗僀悢楍俥3 偺崁悢偼丄丂侾亄冇乮侾乯亄冇乮俀乯亄冇乮俁乯亖俆
埲壓丄摨條偵偟偰丄
丂僼傽儗僀悢楍俥4 偺崁悢偼丄俈
丂僼傽儗僀悢楍俥5 偺崁悢偼丄侾侾
丂僼傽儗僀悢楍俥6 偺崁悢偼丄侾俁
丂僼傽儗僀悢楍俥7 偺崁悢偼丄侾俋
丂僼傽儗僀悢楍俥8 偺崁悢偼丄俀俁
丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
偱偁傞丅
丂堦斒偵丄僼傽儗僀悢楍俥値 偺崁悢偼丄戝懱丂俁値2/兾2丂埵偱偁傞偙偲偑抦傜傟偰偄傞丅
値亖侾丂偺偲偒丄丂俁値2/兾2亖俁/兾2佮侽丏俁丂丂乮幚嵺偺崁悢偼丄俀乯
値亖俀丂偺偲偒丄丂俁値2/兾2亖侾俀/兾2佮侾丏俀丂丂乮幚嵺偺崁悢偼丄俁乯
値亖俁丂偺偲偒丄丂俁値2/兾2亖俀俈/兾2佮俀丏俈丂丂乮幚嵺偺崁悢偼丄俆乯
値亖係丂偺偲偒丄丂俁値2/兾2亖係俉/兾2佮係丏俋丂丂乮幚嵺偺崁悢偼丄俈乯
値亖俆丂偺偲偒丄丂俁値2/兾2亖俈俆/兾2佮俈丏俇丂丂乮幚嵺偺崁悢偼丄侾侾乯
値亖俇丂偺偲偒丄丂俁値2/兾2亖侾侽俉/兾2佮侾侽丏俋丂丂乮幚嵺偺崁悢偼丄侾俁乯
値亖俈丂偺偲偒丄丂俁値2/兾2亖侾係俈/兾2佮侾係丏俋丂丂乮幚嵺偺崁悢偼丄侾俋乯
値亖俉丂偺偲偒丄丂俁値2/兾2亖侾俋俀/兾2佮侾俋丏俆丂丂乮幚嵺偺崁悢偼丄俀俁乯
乮彫偝偄 値 偵偮偄偰偼丄慡慠墦偄偐側丏丏丏倖(^_^;)丂乯
丂忋婰偱丄悢 侽 傪暘悢 侽/侾 偱昞偟偨傛偆偵丄惓偺柍尷戝乮亄亣乯傪暘悢 侾/侽
偱昞偡偙偲偵
偡傞丅偙偺偲偒丄俀偮偺婛栺暘悢 倎/倐 丆們/倓 偐傜丄怴偟偄婛栺暘悢 乮倎亄們乯/乮倐亄倓乯 偑弴師
惗惉偝傟傞丅
| 0/1 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
1/0 |
| 丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
1/1 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
丂 |
丂 |
1/2 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
2/1 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
1/3 |
丂 |
丂 |
丂 |
2/3 |
丂 |
丂 |
丂 |
3/2 |
丂 |
丂 |
丂 |
3/1 |
丂 |
丂 |
| 丂 |
1/4 |
丂 |
2/5 |
丂 |
3/5 |
丂 |
3/4 |
丂 |
4/3 |
丂 |
5/3 |
丂 |
5/2 |
丂 |
4/1 |
丂 |
丂忋婰昞偺峔惉曽朄偐傜丄弌尰偡傞暘悢偼慡偰憡堎側傞丅
忋婰昞傪丄僗僞乕儞=僽儘僐僢僩乮俽倲倕倰値-俛倰倧們倧倲乯偺栘峔憿偲偄偆丅
侽/侾丂偐傜丂侾/侾丂傑偱偵拲栚偡傞偲丄僼傽儗僀悢楍偺奺崁偑戝偒偝偺弴偵弌尰偟偰偄傞丅
丂忋婰昞偺懢帤偺悢楍偑丄僼傽儗僀悢楍 俥4 偱丄崁悢偼丄俈 偱偁傞丅
丂忋婰偺昞偐傜丄師偺惈幙偑惉傝棫偮偙偲偑悇嶡偝傟傞丅
丂俀偮偺婛栺暘悢 倎/倐 丆們/倓 偑丄偁傞僼傽儗僀悢楍偺椬傝崌偆俀崁偱偁傞偲偒丄拞娫
暘悢 乮倎亄們乯/乮倐亄倓乯 偼僼傽儗僀悢楍偺 俥b+d 偺崁偲側傞
椺丂暘悢 侾/俀丂偲丂俀/俁 偼丄僼傽儗僀悢楍 俥3 偺椬傝崌偆俀崁偱偁傞偑丄偦偺拞娫暘悢
丂丂俁/俆 偼丄僼傽儗僀悢楍 俥5 偺崁偵側偭偰偄傞丅
乮捛婰乯丂暯惉侾俋擭俆寧俁侽擔晅偗
丂忋婰偱偼丄慡偔婡夿揑偵僼傽儗僀悢楍偺奺崁傪寁嶼偟偨偑丄婔壗妛揑偵師偺傛偆側堄枴
崌偄偑偁傞偙偲傪嵟嬤抦傞偙偲偑偱偒偨丅
丂摉俫俹偺乽暯惉侾俆擭搙慜婜丂搶嫗戝妛丂棟壢宯乿偺栤戣偱偍悽榖偵側偭偨搶嫗戝妛偺捸
堜愭惗偑僼傽儗僀悢楍傪婔壗揑偵愢柧偝傟偰偄傞丅乮擔杮悢妛夛巗柉島墘夛俀侽侽俇乯
丂壓恾偼丄俀偮偺墌丂俠1丗倶2亄乮倷亅侾/俀乯2亖乮侾/俀乯2丂丂俠2丗乮倶亅侾乯2亄乮倷亅侾/俀乯2亖乮侾/俀乯2
偲 倶 幉偵懳偟偰弴師奜愙偡傞墌傪昤偄偨傕偺偱偁傞丅
丂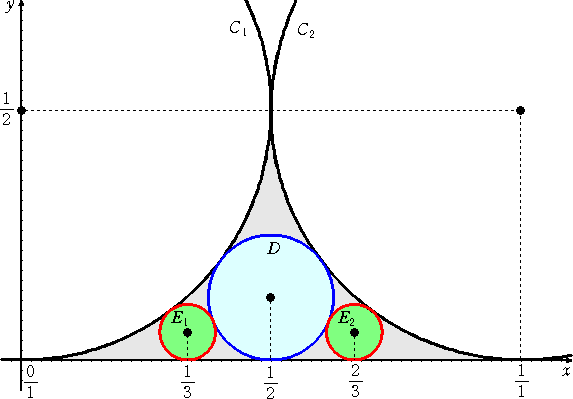
丂偙偺偲偒丄墌 俢 偺拞怱偺倶 嵗昗偼丄侾/俀 偱丄墌 俤1 偺拞怱偺 倶 嵗昗偼丄侾/俁 丄墌 俤2 偺
拞怱偺 倶 嵗昗偼丄侾/俁 偲側傞偙偲偵嬃偐偝傟傞丅
丂偙傟偼丄惓偵僼傽儗僀悢楍偺俥3 側偺偩両
丂幚嵺偵丄庤寁嶼偱偙偺偙偲傪妋擣偟偰傒傛偆丅
丂墌 俢 偺拞怱偺 倶 嵗昗偑丄侾/俀 偱偁傞偙偲偼柧傜偐偩傠偆丅墌 俢 偺敿宎傪
俼 偲偡傞偲丄
嶰暯曽偺掕棟傛傝丄丂乮侾/俀亅俼乯2亄乮侾/俀乯2亖乮侾/俀亄俼乯2丂偑惉傝棫偮丅
丂偙傟傛傝丄丂俼亖侾/俉丂偱偁傞丅
傑偨丄墌 俤1 偺敿宎傪 倰 丄拞怱 俤1 偺 倶 嵗昗傪 倎 偲偡傞偲丄嶰暯曽偺掕棟傛傝丄
丂乮侾/俀亅倰乯2亄倎2亖乮侾/俀亄倰乯2丂丄乮侾/俀亅倎乯2亄乮侾/俉亅倰乯2亖乮侾/俉亄倰乯2
偑惉傝棫偮丅偙傟傛傝丄
丂倎2亖俀倰丂丂丄丂丂倎2亅倎亄侾/係亖倰/俀
戞俀幃傛傝丄丂係倎2亅係倎亄侾亖俀倰丂側偺偱丄丂係倎2亅係倎亄侾亖倎2
偡側傢偪丄丂俁倎2亅係倎亄侾亖侽
傛偭偰丄丂乮俁倎亅侾乯乮倎亅侾乯亖侽丂傛傝丄丂倎亖侾/俁丂丄侾
倎亖侾丂偼晄揔側偺偱丄丂倎亖侾/俁
丂摨條偵偟偰丄拞怱 俤2 偺 倶 嵗昗偑 俀/俁 偱偁傞偙偲傕帵偝傟傞丅
傑偨丄墌丂俠1 偲墌 俤1 偍傛傃 倶 幉偵愙偡傞墌偺拞怱偺 倶 嵗昗傪 倐 丄敿宎傪 倱 偲偡傞偲丄
忋婰偲摨條偺寁嶼偐傜丄
丂倐2亖俀倱丂丄倐2亅乮俀/俁乯倐亄侾/俋亖俀倱/俋
偑摼傜傟丄偙傟傪夝偄偰丄丂倐亖侾/係丂丄丂倱亖侾/俁俀丂偲側傞丅
乮僐儊儞僩乯丂倐亖侾/係丂傕僼傽儗僀悢楍偺俥4 偺崁偱偁傞丅弴師丄尨揰偵嬤偯偄偰峴偔偵偟偨
丂丂丂丂丂丂偑偭偰丄帺慠悢 値 偺媡悢 侾/値 偑墌偺拞怱偺 倶 嵗昗傪梌偊偰偄傞揰丄偝傜偵
丂丂丂丂丂丂敿宎偑 侾/(2値2) 偺傛偆側暤埻婥偱偁傞揰偑偲偰傕柺敀偄丅
丂丂忋恾偺墌偺偙偲傪丄僼僅乕僪偺墌乮俥倧倰倓丂們倝倰們倢倕乯偲尵偆傜偟偄丅
丂偙偺偙偲傪堦斒揑偵徹柧偟偰傒傛偆丅
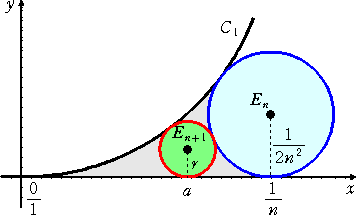 |
丂墌 俤値 偺拞怱偺 倶 嵗昗偑丄侾/値
偱丄敿宎偑 侾/(2値2) 丂偱偁傞偲偒丄
墌 俤値+1 偺拞怱偺 倶 嵗昗偲敿宎偼
偦傟偧傟
丂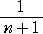 丂丂丄丂 丂丂丄丂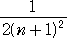
偱梌偊傜傟傞偙偲傪帵偡丅
|
嶰暯曽偺掕棟傛傝丄
丂乮侾/俀亅倰乯2亄倎2亖乮侾/俀亄倰乯2丂丄乮侾/値亅倎乯2亄乮侾/(2値2)亅倰乯2亖乮侾/(2値2)亄倰乯2
偑惉傝棫偮丅偙傟傛傝丄丂倎2亖俀倰丂丄丂倎2亅乮俀/値乯倎亄侾/値2亖俀倰/値2
戞俀幃傛傝丄丂値2倎2亅俀値倎亄侾亖俀倰丂側偺偱丄丂値2倎2亅俀値倎亄侾亖倎2
偡側傢偪丄丂乮値2亅侾乯倎2亅俀値倎亄侾亖侽
傛偭偰丄丂乮乮値亄侾乯倎亅侾乯乮乮値亅侾乯倎亅侾乯亖侽丂傛傝丄丂倎亖侾/乮値亄侾乯丂丄侾/乮値亅侾乯
丂倎亖侾/乮値亅侾乯丂偼晄揔側偺偱丄丂倎亖侾/乮値亄侾乯
偙偺偲偒丄敿宎偼丄侾/乮俀乮値亄侾乯2乯丂偲側傞丅
乮僐儊儞僩乯丂徹柧傪挱傔偰偄傞偲丄崱峏側偑傜偵旤偟偄寢壥偱偡偹両捸堜愭惗偵姶幱偟傑偡丅
丂偝偰丄榖傪尦偵栠偦偆丅忋婰偱弎傋偨傛偆偵丄壓昞偺傛偆偵拞娫暘悢偑庬乆摼傜傟偨丅
| 0/1 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
1/0 |
| 丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
1/1 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
丂 |
丂 |
1/2 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
2/1 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
1/3 |
丂 |
丂 |
丂 |
2/3 |
丂 |
丂 |
丂 |
3/2 |
丂 |
丂 |
丂 |
3/1 |
丂 |
丂 |
| 丂 |
1/4 |
丂 |
2/5 |
丂 |
3/5 |
丂 |
3/4 |
丂 |
4/3 |
丂 |
5/3 |
丂 |
5/2 |
丂 |
4/1 |
丂 |
丂偙偺拞娫暘悢偵怴偟偄奣擮偑師偺傛偆偵晅壛偝傟傞丅
丂俀偮偺暘悢 倎/倐亙們/倓 偵懳偟偰丄惓偺悢 倫 丄倯 傪梡偄偰嶌傜傟傞暘悢
乮倫倎亄倯們乯/乮倫倐亄倯倓乯丂偼丄晄摍幃 倎/倐亙乮倫倎亄倯們乯/乮倫倐亄倯倓乯亙們/倓 傪枮偨偡丅
丂幚嵺偵丄丂乮倫倎亄倯們乯/乮倫倐亄倯倓乯亅倎/倐
亖乷乮倫倎亄倯們乯倐亅乮倫倐亄倯倓乯倎乸/乮倫倐亄倯倓乯倐亖倯乮倐們亅倎倓乯/乮倫倐亄倯倓乯倐亜侽
側偺偱丄丂倎/倐 亙 乮倫倎亄倯們乯/乮倫倐亄倯倓乯丂偑惉傝棫偮丅
丂乮倫倎亄倯們乯/乮倫倐亄倯倓乯 亙 們/倓 丂傕摨條偵惉傝棫偮丅
丂偙偺偲偒丄暘悢 乮倫倎亄倯們乯/乮倫倐亄倯倓乯 偺偙偲傪丄
俀偮偺暘悢 倎/倐亙們/倓 偵懳偡傞廳傒 倫 丗 倯 偺拞娫暘悢偲偄偆丅
椺丂丂忋婰偺昞偵偍偄偰丄
丂暘悢 侾/侾 偼丄俀偮偺暘悢 侽/侾 丄 侾/侽 偵懳偟偰丄廳傒 侾 丗 侾 偺拞娫暘悢偱偁傞丅
丂暘悢 侾/俀 偼丄俀偮偺暘悢 侽/侾 丄 侾/侽 偵懳偟偰丄廳傒 俀 丗 侾 偺拞娫暘悢偱偁傞丅
丂暘悢 侾/俀 偼丄俀偮偺暘悢 侽/侾 丄 侾/侾 偵懳偟偰丄廳傒 侾 丗 侾 偺拞娫暘悢偱偁傞丅
丂暘悢 侾/俁 偼丄俀偮偺暘悢 侽/侾 丄 侾/侽 偵懳偟偰丄廳傒 俁 丗 侾 偺拞娫暘悢偱偁傞丅
丂暘悢 侾/俁 偼丄俀偮偺暘悢 侽/侾 丄 侾/侾 偵懳偟偰丄廳傒 俀 丗 侾 偺拞娫暘悢偱偁傞丅
丂暘悢 侾/俁 偼丄俀偮偺暘悢 侽/侾 丄 侾/俀 偵懳偟偰丄廳傒 侾 丗 侾 偺拞娫暘悢偱偁傞丅
丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
丂偙偺寁嶼偐傜丄
丂暘悢 侾/俀 偼丄俀偮偺暘悢 侽/侾 丄 侾/侾 偺娫偵偁傞
丂暘悢 侾/俁 偼丄俀偮偺暘悢 侽/侾 丄 侾/俀 偺娫偵偁傞
偙偲偑暘偐傞丅
丂摨條偵偟偰丄
丂暘悢 俀/俁 偼丄俀偮偺暘悢 侽/侾 丄 侾/侽 偵懳偟偰丄廳傒 俁 丗 俀 偺拞娫暘悢偱偁傞丅
丂暘悢 俀/俁 偼丄俀偮偺暘悢 侽/侾 丄 侾/侾 偵懳偟偰丄廳傒 侾 丗 俀 偺拞娫暘悢偱偁傞丅
丂暘悢 俀/俁 偼丄俀偮偺暘悢 侾/俀 丄 侾/侾 偵懳偟偰丄廳傒 侾 丗 侾 偺拞娫暘悢偱偁傞丅
丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
丂偙偺寁嶼偐傜丄
丂暘悢 俀/俁 偼丄俀偮偺暘悢 侽/侾 丄 侾/侾 偺娫偵偁傞
丂暘悢 俀/俁 偼丄俀偮偺暘悢 侾/俀 丄 侾/侾 偺娫偵偁傞
偙偲偑暘偐傞丅
丂傑偨丄廳傒偺曄壔偵拝栚偡傞偲師偺傛偆偵曄壔偟偰偄傞丅
丂偨偲偊偽丄
丂丂暘悢 侾/俁 偺応崌偼丄 俁 丗 侾 仺 俀 丗 侾 仺 侾 丗 侾
丂丂暘悢 俀/俁 偺応崌偼丄 俁 丗 俀 仺 侾 丗 俀 仺 侾 丗 侾
丂偙偺偙偲傪堦斒壔偡傞偲丄廳傒偑摍偟偔側傞傑偱偼丄
丂丂丂丂戝 丗 彫 乮 彫 丗 戝 乯 仺 戝亅彫 丗 彫 乮 彫 丗 戝亅彫 乯
偲曄壔偟偰偄傞傛偆偩丅
丂埲忋傪傑偲傔偰丄暘悢 俀/俁 偺摦岦傪奊偵偟偰傒偨丅
丂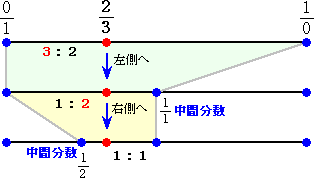
丂偙偺傛偆偵廳傒 倫 丗 倯 偺抣擛壗偵傛偭偰丄忋偐傜壓偵悈偑偟偨偨傝棊偪傞傛偆偵丄暘悢偺
棊偪拝偒愭乮廳傒偑 侾 丗 侾 偵側傞傑偱乯偑掕傑偭偰偄偔偙偲偼丄偲偰傕柺敀偄尰徾偩丅
楙廗栤戣俙丂丂廳傒偺曄壔偵拝栚偟偰丄暘悢 俁/俆 偼丄偳偺傛偆偵曄壔偡傞偐丠
乮摎乯丂丂俆 丗 俁 仺 俀 丗 俁 仺 俀 丗 侾 仺 侾 丗 侾
楙廗栤戣俛丂丂嵍懁戝仺塃懁戝仺嵍懁戝仺廳傒 侾 丗 侾 丂偲廳傒偑曄壔偡傞偲偒弌敪揰偺
丂丂丂丂丂丂丂丂暘悢傪媮傔傛丅
乮摎乯丂丂侾 丗 侾 仺 俀 丗 侾 仺 俀 丗 俁 仺 俆 丗 俁丂傛傝丄媮傔傞暘悢偼丄俁/俆
丂楙廗栤戣俙丄俛 偐傜傕暘偐傞傛偆偵丄暘悢 俁/俆 偲 廳傒偺曄壔偼 侾 丗 侾 偵懳墳偟偰偄傞偲
尵偊傞丅
丂偦偙偱丄廳傒偑嵍懁戝偺偲偒偼悢帤偺乽侽乿傪丄塃懁戝偺偲偒偼悢帤偺乽侾乿傪懳墳偯偗傞傕
偺偲偡傞偲丄
丂暘悢 俁/俆 偵偼丄丂悢偺暲傃 侽侾侽丂偑懳墳偡傞
椺丂暘悢 俁/係 偵懳墳偡傞悢偺暲傃傪媮傔傛丅
丂丂係 丗 俁 仺 侾 丗 俁 仺 侾 丗 俀 仺 侾 丗 侾丂側偺偱丄丂侽侾侾丂偑懳墳偡傞丅
丂偲偙傠偱丄暘悢 俁/係 偵偮偄偰丄
丂俁亖係亊侽亄俁丂丄係亖俁亊侾亄侾丂丄俁亖侾亊俁
偐傜丄暘悢 俁/係 偺楢暘悢昞帵偼丄乵 侽 丟 侾 丆 俁 乶 偲側傞丅
丂廳傒偺曄壔偺寁嶼偱偼弴師戝偒偄悢偐傜彫偝偄悢傪堷偄偰偄傞偑丄偙傟偼妱傝嶼傪偟偰
乽梋傝乿偵姺嶼偟偰偄傞偙偲偵摍偟偄丅
丂嵟屻偼丄梋傝乽侽乿偺堦曕庤慜偱寁嶼偑廔椆偡傞偺偱丄幚幙偼丄
丂俁亖係亊侽亄俁丂丄係亖俁亊侾亄侾丂丄俁亖侾亊俀亄侾
偲偄偆寁嶼偵摍偟偄丅
丂偦偙偱丄戞侾峴偵偼丄悢偺乽侾乿傪懳墳偝偣丄偙傟偑乽侽乿夞丄
丂戞俀峴偵偼丄悢偺乽侽乿傪懳墳偝偣丄偙傟偑乽侾乿夞丄
丂戞俁峴偵偼丄悢偺乽侾乿傪懳墳偝偣丄偙傟偑乽俀乿夞丄
偲東栿偡傟偽丄丂侽侾侾丂偲偄偆悢偺暲傃偑弌尰偡傞丅
椺丂暘悢 俁/俆 偵偮偄偰傕摨條側寁嶼偱丄悢偺暲傃傪尒偄偩偣丅
丂俁亖俆亊侽亄俁丂丄俆亖俁亊侾亄俀丂丄俁亖俀亊侾亄侾丂丄俀亖侾亊侾亄侾
丂埲忋偐傜丄媮傔傞悢偺暲傃偼丄丂侽侾侽丂偲側傞丅
丂暘悢 俁/俆 偺楢暘悢昞帵偑丄乵 侽 丟 侾 丆 侾 丆 俀 乶 偱偁傞偙偲傪峫偊傞偲丄
丂暘悢 俻/俹丂偺楢暘悢昞帵偑丄乵 倎 丟 倐 丆 們 丆丒丒丒丆 倓 乶 偱偁傞偲偒丄
暘悢 俻/俹丂偵懳墳偡傞悢偺暲傃偼丄
侾 傪 倎 屄 丄 侽 傪 倐 屄 丄 侾 傪 們 屄 丄 丒丒丒 丄 侾 傑偨偼 侽 傪
倓亅侾 屄暲傋偨傕偺
偲側傞偙偲偑暘偐傞丅
丂慜偵偁偘偨昞
| 0/1 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
1/0 |
| 丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
1/1 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
丂 |
丂 |
1/2 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
2/1 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
1/3 |
丂 |
丂 |
丂 |
2/3 |
丂 |
丂 |
丂 |
3/2 |
丂 |
丂 |
丂 |
3/1 |
丂 |
丂 |
| 丂 |
1/4 |
丂 |
2/5 |
丂 |
3/5 |
丂 |
3/4 |
丂 |
4/3 |
丂 |
5/3 |
丂 |
5/2 |
丂 |
4/1 |
丂 |
偵偍偄偰丄丂侽/侾 丄 侾/侾 丄 侾/侽丂埲奜偺暘悢偵偮偄偰丄悢偺暲傃偵抲偒姺偊偰傒傞偲丄
| 0/1 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
1/0 |
| 丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
1/1 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
丂 |
丂 |
侽 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
侾 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
00 |
丂 |
丂 |
丂 |
01 |
丂 |
丂 |
丂 |
10 |
丂 |
丂 |
丂 |
11 |
丂 |
丂 |
| 丂 |
000 |
丂 |
001 |
丂 |
010 |
丂 |
011 |
丂 |
100 |
丂 |
101 |
丂 |
110 |
丂 |
111 |
丂 |
丂椬傝崌偆暘悢 侾/俀 偲 俀/俁 偺拞娫暘悢偲偟偰丄暘悢 俁/俆 偑嶌傜傟偨傢偗偩偑丄暘悢 俁/俆
偺悢偺暲傃偑 侽侾侽 偱丄暘悢 侾/俀丄俀/俁 偺悢偺暲傃偑偦傟偧傟 侽 偲 侽侾 偱偁傞偙偲傪峫偊
傞偲丄暘悢偺棊偪拝偒愭偑丄侽侾侽 仺 侽 偲 侽侾 傪抂揰偵傕偮斖埻偵側傞傕偺偲悇嶡偝傟傞丅
丂偡側傢偪丄乽侽侾侽乿偼乽侽侾乿偺嵍懁偱丄偐偮丄乽侽侾侽乿偼乽侽乿偺塃懁偵埵抲偡傞丅
丂悢妛僙儈僫乕丂俀侽侽俈擭俁寧崋偱丄愺堜揘栫偝傫偼丄乽僄儗僈儞僩側夝摎傪傕偲傓乿偵丄師偺
傛偆側栤戣傪弌戣偝傟偨丅
丂暘曣偑侾侽侽埲壓偺偡傋偰偺婛栺暘悢偑戝偒偝偺弴偵暲傫偱偄傞丅暘悢 侾俈/俇俇 偺
椉椬傝偺暘悢傪媮傔傛丅
丂偙傟傑偱偵妛傫偩棟榑傪偙偺栤戣偵揔梡偟偰傒傛偆丅
傑偢丄侾俈亖俇俇亊侽亄侾俈丂丄俇俇亖侾俈亊俁亄侾俆丂丄侾俈亖侾俆亊侾亄俀丂丄侾俆亖俀亊俈亄侾
丂丂丂俀亖侾亊侾亄侾
丂埲忋偐傜丄暘悢 侾俈/俇俇 偵懳墳偡傞悢偺暲傃偼丄侽侽侽侾侽侽侽侽侽侽侽侾 偲側傞丅
偟偨偑偭偰丄椉椬傝偺暘悢偵懳墳偡傞悢偺暲傃偼丄
丂侽侽侽侾侽侽侽侽侽侽侽丂丂侽侽侽侾侽侽侽侽侽侽
偲側傞偼偢偱偁傞丅
丂偙傟傜偺楢暘悢昞帵偼丄偦傟偧傟丂乵 侽 丟 俁 丆 侾 丆 俉 乶 丄乵 侽 丟 俁 丆 侾 丆 俈 乶 側偺偱丄暘
悢偵捈偣偽丄偦傟偧傟丄 俋/俁俆 丄 俉/俁侾 偲側傞丅
丂偙偺偲偒丄俀偮偺暘悢 俋/俁俆 丄 俉/俁侾 偼丄 俋亊俁侾亅俉亊俁俆亖亅侾 傛傝椬傝崌偆暘悢偱丄
暘悢 侾俈/俇俇 偼丄偦傟傜偺拞娫暘悢偱偁傞丅
丂偝傜偵丄俀偮偺暘悢 俋/俁俆 丄 侾俈/俇俇 偺拞娫暘悢傪峫偊傞偲丄 俀俇/侾侽侾 偲側傝丄偙傟偼丄
暘曣偑侾侽侽埲壓偲偄偆忦審偵斀偡傞偐傜晄揔偱偁傞丅
丂摨條偵丄俀偮偺暘悢 侾俈/俇俇 偲 俉/俁侾 偺拞娫暘悢 俀俆/俋俈 傪峫偊傞偲丄暘悢
俉/俁侾 傛
傝暘悢 俀俆/俋俈 偺曽偑丄傛傝暘悢 侾俈/俇俇 偵嬤偄丅
丂埲忋偐傜丄
丂暘曣偑侾侽侽埲壓偺偡傋偰偺婛栺暘悢傪戝偒偝偺弴偵暲傋偨偲偒丄
丂暘悢 侾俈/俇俇 偺椉椬傝偺暘悢偼丄俋/俁俆 偲 俀俆/俋俈 偱偁傞
偙偲偑帵偝傟偨丅
丂忋婰偺栤戣偵偮偄偰丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽峌棯朄乿偝傫偐傜儗億乕僩傪
捀偄偨丅乮暯惉俀俀擭侾俀寧俈擔晅偗乯
丂倷/倶丄侾俈/俇俇 乮偨偩偟丄 倷/倶亙侾俈/俇俇乯丂偑椬傝崌偆暘悢偐傜丄丂侾俈倶亅俇俇倷亖侾丂偲側傞丅
晄掕曽掱幃丂侾俈倶亅俇俇倷亖侾丂傪夝偔偲丄堦斒夝偼丄
丂倶亖俁俆亄俇俇倲丂丄丂倷亖俋亄侾俈倲丂丂乮倲 偼惍悢乯
丂侾俈/俇俇偺曅曽偺恊偼丄俥66偱偼丄丂侽亙倶亙俇俇丂偩偐傜丄丂倲亖侽丂偺丂俋/俁俆丂偲側傞丅
傕偆侾偮偼丄僼傽儗僀悢楍偺拞娫暘悢偺惗惉曽朄偐傜丄
丂暘巕亖俋亄們亖侾俈丂丄丂暘曣亖俁俆亄倓亖俇俇丂傛傝丄丂俉/俁侾丂偱偁傞丅
丂傛偭偰丄丂俋/俁俆丄侾俈/俇俇丄俉/俁侾丂偱偁傞丅
丂傑偨丄俥100
偲偡傞偲丄侾俈/俇俇丄俀俆/俋俈丄俉/俁侾丂偲拞娫暘悢偑偱偒傞丅
乮僐儊儞僩乯丂俁擭敿傇傝偵偙偺儁乕僕傪尒偰丄傑偩傑偩彂偒懌傝側偄偲偙傠偑偁傞傛偆側丏丏丏梊
丂丂丂丂丂丂姶両峌棯朄偝傫偵姶幱偟傑偡丅
丂峌棯朄偝傫偐傜偺曗懌偱偡丅乮暯惉俀俀擭侾俀寧俉擔晅偗乯
丂晄掕曽掱幃丂侾俈倶亅俇俇倷亖侾丂乮 倷/倶亙侾俈/俇俇 偱椬傝崌偆暘悢乯偺堦斒夝
丂丂丂倶亖俁俆亄俇俇倲丂丄丂倷亖俋亄侾俈倲丂丂乮倲 偼惍悢乯
偼丄倲亖侽丄侾丄俀丄俁丄丒丒丒丂偲偡傞偲丄丂俋/俁俆丄丒丒丒丄侾俈/俇俇丂偺拞娫暘悢傪惗惉偡傞丅
| 倲 |
侽 |
侾 |
俀 |
俁 |
丒丒丒 |
亣 |
| 倷 |
俋 |
俋亄侾俈 |
俋亄侾俈亊俀 |
俋亄侾俈亊俁 |
丒丒丒 |
侾俈 |
| 倶 |
俁俆 |
俁俆亄俇俇 |
俁俆亄俇俇亊俀 |
俁俆亄俇俇亊俁 |
丒丒丒 |
俇俇 |
摨條偵丄侾俈/俇俇亙倷/倶丂偼椬傝崌偆暘悢偐傜丄丂亅侾俈倶亄俇俇倷亖侾丂偲側傞丅堦斒夝偼丄
丂倶亖俁侾亄俇俇倲丂丄丂倷亖俉亄侾俈倲丂丂乮倲 偼惍悢乯
偱丄倲亖侽丄侾丄俀丄俁丄丒丒丒丂偲偡傞偲丄丂侾俈/俇俇丄丒丒丒丄俉/俁侾丂偺拞娫暘悢傪惗惉偡傞丅
| 倲 |
侽 |
侾 |
俀 |
俁 |
丒丒丒 |
亣 |
| 倷 |
俉 |
俉亄侾俈 |
俉亄侾俈亊俀 |
俉亄侾俈亊俁 |
丒丒丒 |
侾俈 |
| 倶 |
俁侾 |
俁侾亄俇俇 |
俁侾亄俇俇亊俀 |
俁侾亄俇俇亊俁 |
丒丒丒 |
俇俇 |
乮捛婰乯丂椷榓俁擭俋寧俀俇擔晅偗
丂悢妛僙儈僫乕丂俀侽俀侾擭俈寧崋偱丄嶳揷廋巌偝傫偼丄乽僄儗僈儞僩側夝摎傪傕偲傓乿偵丄偙偺
儁乕僕偺榖戣偵娭楢偡傞栤戣傪弌戣偝傟偨丅
丂桳棟悢 倱丄倲 乮倱亙倲乯偑婛栺暘悢偱 倱亖倎/倐丄倲亖們/倓 偲昞偝傟傞偲偒丄
丂倣亖倱仈倲亖乮倎亄們乯/乮倐亄倓乯
偲掕傔傞丅奐嬫娫 俬 亖乮倱丆倲乯偵懳偟偰丄丂倱亙倣亙倲丂偑惉傝棫偪丄倳 傪奐嬫娫 俬 偺仈拞揰偲
屇傇偙偲偵偡傞丅
丂偙偺偲偒丄奐嬫娫 俬 偼丄仈拞揰偲俀偮偺奐嬫娫乮倱丆倳乯丄乮倳丆倲乯偵暘妱偝傟傞丅偡側傢偪丄
丂俬 亖乮倱丆倳乯倀乷倳乸倀乮倳丆倲乯
椺丂奐嬫娫 俬 亖乮侾/俀丆俀/俁乯偵懳偟偰丄丂倳亖乮侾/俀乯仈乮俀/俁乯亖俁/俆丂側偺偱丄
侾夞栚偺暘妱偼丄丂俬俴亖乮侾/俀丆俁/俆乯丄俬俼亖乮俁/俆丆俀/俁乯
俀夞栚偺暘妱偼丄丂俬俴俴亖乮侾/俀丆係/俈乯丄俬俴俼亖乮係/俈丆俁/俆乯丄
丂丂丂丂丂丂丂丂丂丂丂俬俼俴亖乮俁/俆丆俆/俉乯丄俬俼俼亖乮俆/俉丆俀/俁乯
丂偙偺偲偒丄丂俬俼俴亖乮俁/俆丆俆/俉乯丂偵偍偗傞仈拞揰偼丄俉/侾俁偲側傝丄
乽俉/侾俁乿偼奐嬫娫 俬 亖乮侾/俀丆俀/俁乯偵偍偗傞傾僪儗僗偲偟偰丄乽俼俴乿傪帩偮丅
丂偙偙偱丄丂俉/侾俁亖乮俀丒侾亄俀丒俀乯/乮俁丒俀亄俁丒俁乯丂偱偁傞偺偱丄俉/侾俁偼丄
丂俀偮偺暘悢 侾/俀亙俀/俁 偵懳偡傞廳傒 俀 丗 俁 偺拞娫暘悢偲側傞丅
丂廳傒偑嵍懁戝偺偲偒偼悢帤偺乽侽乿傪丄塃懁戝偺偲偒偼悢帤偺乽侾乿傪懳墳偯偗傞傕偺偲偡
傞偲丄
丂丂俀 丗 俁 仺 俀 丗 侾丂側偺偱丄暘悢 俉/侾俁 偵偼 侾侽 偑懳墳偡傞丅
丂悢帤偺乽侽乿傪俴丄悢帤偺乽侾乿傪俼偲懳墳偯偗傟偽丄偙傟偼丄傑偝偵傾僪儗僗乽俼俴乿傪帩偮偙偲
傪堄枴偡傞丅
丂乽僄儗僈儞僩側夝摎傪傕偲傓乿偱偺弌戣偱偼丄
丂奐嬫娫 俬 撪偺慡偰偺桳棟悢偼傾僪儗僗傪帩偮偙偲傪帵偣丅
偲側偭偰偄傞丅
丂乽僄儗僈儞僩側夝摎傪傕偲傓乿偵偍偄偰丄師偺奣擮偑嫽枴怺偄丅
丂俀偮偺婛栺暘悢 倎/倐丄們/倓 偵懳偟偰丄偦傟傜偺夝棧搙傪
丂儮乮倎/倐丄們/倓乯亖倐們亅倎倓
偱掕傔傞丅
椺丂儮乮侾/俁丆侾/俀乯亖俁亅俀亖侾 傛傝丄夝棧搙偼侾偱丄俀偮偺暘悢偼椬傝崌偭偰偄傞丅
丂儮乮侾/俁丆俀/俁乯亖俇亅俁亖俁丂傛傝丄夝棧搙偼俁偱丄俀偮偺暘悢偼椬傝崌偭偰偄側偄丅
丂摉俫俹撉幰偺俲丏俽丏偝傫偐傜丄僼傽儗僀悢楍偵娭偡傞榖戣傪儊乕儖偱捀偄偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俁擭侾侽寧俈擔晅偗乯
丂僼傽儗僀悢楍偵偍偄偰丄
丂悢楍 俥1 丗 侽/侾丆侾/侾丂傛傝丄暘巕偺榓亖侾丄暘曣偺榓亖俀丂偱偁傞丅
丂悢楍 俥2 丗 侽/侾丆侾/俀丆侾/侾丂傛傝丄暘巕偺榓亖俀丄暘曣偺榓亖係丂偱偁傞丅
丂悢楍 俥3 丗 侽/侾丆侾/俁丆侾/俀丆俀/俁丆侾/侾丂傛傝丄暘巕偺榓亖俆丄暘曣偺榓亖侾侽丂偱偁傞丅
丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
丂偙偺偙偲偐傜丄師偺柦戣偑惉傝棫偮偙偲偑梊憐偝傟傞丅
柦丂戣丂丂僼傽儗僀悢楍偵偍偄偰丄乮暘巕偺榓乯/乮暘曣偺榓乯亖侾/俀丂偑惉傝棫偮丅
丂帺慠悢 値 偵娭偡傞悢妛揑婣擺朄偱徹柧偱偒傞丅
乮徹柧乯丂値亖侾 偺偲偒丄柧傜偐偵惉傝棫偮丅
丂値亖倠乮倠亞侾乯偺偲偒丄柦戣偑惉傝棫偮偲壖掕偡傞丅偡側傢偪丄
丂悢楍 俥倠 偵偍偄偰丄乮暘巕偺榓乯/乮暘曣偺榓乯亖侾/俀
丂値亖倠亄侾丂偲偡傞丅暘曣偑丄倠傑偱偺僼傽儗僀悢楍偺暘曣偺榓亖A丄暘巕偺榓亖B偲偡傞偲丄
丂婣擺朄偺壖掕傛傝丄B/A亖1/俀丂側偺偱丄丂俙亖俀俛
丂堦曽丄倠亄侾傪暘曣偵帩偮婛栺暘悢偼丄僆僀儔乕偺娭悢偐傜丄兂乮倠亄侾乯屄偁傝丄暘曣偺榓
丂偼丄乮倠亄侾乯兂乮倠亄侾乯偲側傞丅
丂丂堦斒偵丄値/倣 偑婛栺偱偁傟偽丄(倣亅値)/倣 傕婛栺偱偁傞偺偱丄暘曣偑 倠亄侾 偺偲偒偺
丂婛栺側暘悢偺暘巕偺榓偼丄摍嵎悢楍偺榓偺媮傔曽偲摨條偺曽朄乮僈僂僗偺曽朄乯傪梡偄偰丄
丂丂兂乮倠亄侾乯乮侾亄倠乯/俀丂乮丂仼丂崁悢亊乮弶崁亄枛崁乯/俀丂乯
丂偲側傞丅偙偺偲偒丄暘曣亖倠亄侾 偺偲偒偺僼傽儗僀悢楍偺暘曣偺榓亖C丄暘巕偺榓亖D 偲偡
丂傞偲丄D/C亖1/俀丂傛傝丄C亖俀D丂偲側傞丅
丂傛偭偰丄値亖倠亄侾 偺偲偒偺僼傽儗僀悢楍偵偮偄偰丄
丂暘曣偺榓/暘巕偺榓亖(B亄D)/(A亄C)亖(B亄D)/(俀B亄俀D)亖侾/俀
埲忋偵傛傝丄偡傋偰偺帺慠悢 値 偵偮偄偰丄柦戣偑惉傝棫偮丅丂丂乮徹廔乯
乮僐儊儞僩乯丂僼傽儗僀悢楍偺旤偟偄惈幙偱偡偹両俲丏俽丏偝傫偵姶幱偟傑偡丅
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽嬻廙乿偝傫偐傜丄娭楢偡傞榖戣傪捀偄偨丅
乮暯惉俀俆擭俀寧侾侽擔晅偗乯
丂乽椬傝崌偆暘悢乿偵娭楢偡傞廳梫側惈幙偑尒摉偨傜側偐偭偨偺偱徯夘偟傑偡丅摿偵丄乮侾乯偐
傜摫偐傟傞乮俀乯偺惈幙偑偲偰傕柺敀偄偲巚偄傑偡丅
乮侾乯丂暘悢偑椬傝崌偆丂佁丂僼傽儗僀悢楍偺崁偲偟偰椬傝崌偆
丂偡側傢偪丄埲壓偑惉傝棫偮丅(倎丄倐丄們丄倓丗帺慠悢)
丂俀偮偺暘悢 a/b丄c/d 偑(暘悢偲偟偰)椬傝崌偆
丂佁丂|ad-bc|亖1
丂佁丂(0,0)丄(a,b)丄(c,d)丄(a+c,b+d)偱埻傑傟傞暯峴巐曈宍偺柺愊亖1
丂佁丂忋婰偺暯峴巐曈宍偺曈丒撪晹偵偼奿巕揰偑懚嵼偟側偄
丂佁丂a/b 偲 c/d 偺娫偵偼丄Max(b,d)埲壓偺暘曣傪帩偮暘悢偼柍偄
丂佁丂僼傽儗僀悢楍Fn[n=Max(b,d)]偵偍偄偰丄a/b 偲 c/d 偼(崁偲偟偰)椬傝崌偆丅
(嶲峫丗僺僢僋偺掕棟(Wikipedia)丂丄摉俫俹乽僺僢僋偺掕棟乿乯
乮俀乯丂拞娫暘悢偺堄媊
丂a/b 偲 c/d 偑椬傝崌偆帪丄拞娫暘悢 (a+c)/(b+d) 偼丄a/b丄c/d 偲椬傝崌偆丅
丂偦偙偱丄偦傟偧傟偺娫偱乮侾乯傪揔梡偟偰暘偐傞偙偲偼丄
丂拞娫暘悢偼丄a/b 偲 c/d 偺娫偵偁傞嵟傕暘曣偑彫偝偄暘悢
偱偁傞丅
乮捛婰乯丂暯惉俀俆擭侾侾寧侾俇擔晅偗
丂忋婰偱偼丄椬傝崌偆暘悢偵偮偄偰丄偄傠偄傠尒偰偒偨偑丄乽椬傝崌偆乿偲偔傟偽丄傗偼傝弴斣
偵悢偊偨偔側傞偺偑恖忣偩傠偆丅
丂
丂忋恾偺傛偆偵丄暘悢傪暲傋傟偽悢偊傜傟傞乮壜嶼廤崌乯偙偲偼柧傜偐偩偑丄擛壗偣傫丄暘悢
偑廳暋偟偰偄傞偺偱丄偙偺傑傑偱偼僟僽偭偨傑傑悢偊傜傟偰偟傑偆丅僟僽傝偑側偄傛偆偵悢偊傞
偙偲偑偱偒傟偽丄偦偺暘悢偑嵟弶偐傜悢偊偰壗斣栚偐傕暘偐傞偟丄媡偵丄偁傞弴斣偵偁傞暘
悢偑壗偱偁傞偐傕暘偐偭偰偟傑偆丅乮仺丂嶲峫丗乽暘悢偲桳棟悢偺堘偄乿乯
丂偙偺傛偆側柌偺傛偆側偙偲偑壜擻偱偁傞偙偲傪丄師偺彂愋偱嵟嬤抦傞偙偲偑偱偒偨丅
丂帥郪丂弴丂挊丂乽桳棟悢傪僇僂儞僩偡傞悢幃乿丂乮悢妛僙儈僫乕丂乫侾俁擭侾俀寧崋丂(擔杮昡榑幮乯乯
丂娭悢
丂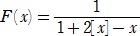
傪梡偄傞偲丄値斣栚偺桳棟悢偼丄丂俥値乮侽乯丂偱梌偊傜傟傞丅
乮椺乯丂侾斣栚偺桳棟悢偼丄俥1乮侽乯亖俥乮侽乯亖侾乮亖侾/侾乯
丂俀斣栚偺桳棟悢偼丄俥2乮侽乯亖俥乮俥乮侽乯乯亖俥乮侾乯亖侾/俀
丂俁斣栚偺桳棟悢偼丄俥3乮侽乯亖俥乮俥乮俥乮侽乯乯乯亖俥乮侾/俀乯亖俀乮亖俀/侾乯
丂係斣栚偺桳棟悢偼丄俥4乮侽乯亖俥乮俥乮俥乮俥乮侽乯乯乯乯亖俥乮俀乯亖侾/俁
丂俆斣栚偺桳棟悢偼丄俥5乮侽乯亖俥乮俥乮俥乮俥乮俥乮侽乯乯乯乯乯亖俥乮侾/俁乯亖俁/俀
丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
乮僐儊儞僩乯丂寁嶼偟偰偄偰丄儚僋儚僋偟偰偒傑偡偹両
乮捛婰乯丂倠倱 偝傫偐傜偛搳峞偄偨偩偒傑偟偨丅乮椷榓俆擭俇寧俋擔晅偗乯
丂俁偮偺暘悢 倶亖倐/a丂丄倷亖倓/們丂丄z=(b+d)/(a+c)丂偵偮偄偰丄倶亙倸亙倷偺偲偒丄倸 偑 x 傛傝偐丄
倷傛傝偐乮嬤偄乯偲偄偆暘悢偺嬤偝傪敾抐偡傞忦審偼偁傝傑偡偐丠
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧俋擔晅偗乯
丂a丄b丄c丄d亜0 偲偟傑偡丅(x+y)/2=b/(2a)+d/(2c)=(ad+bc)/(2ac) 偱偡丅
丂z-(x+y)/2亜0 傪惍棟偡傞偲丄(ad-bc)(c-a)亜0
偙偙偱丄丂x亙y丂偐傜丄ad-bc亜0丂側偺偱丄丂z-(x+y)/2亜0 佁 c亜a
廬偭偰丄a 偲 c 傪斾妑偟偰丄
丂a 偺曽偑戝偒偗傟偽丄x 婑傝丄c 偺曽偑戝偒偗傟偽丄y 婑傝
偲側傝傑偡丅
乮僐儊儞僩乯丂倐/倎亖侾/俀丂丄倓/們亖俀/俁 偵偮偄偰丄丂乮倐亄倓乯/乮倎亄們乯亖俁/俆
丂侾/俀亖侽丏俆丂丄俀/俁亖侽丏俇俈丂丄俁/俆亖侽丏俇丂側偺偱丄暘悢俁/俆偼丄暘悢俀/俁婑傝偱偁傞丅
丂傜偡偐傞偝傫偺寢壥偼丄忋婰偺寁嶼傪偟側偔偰傕丄倎亖俀偲們亖俁偺戝彫娭學丂倎亙們丂傪尒偰丄
弖帪偵丄暘悢俁/俆偼丄暘悢俀/俁婑傝偱偁傞偙偲偑暘偐傞丅
丂倠倱 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾侽擔晅偗乯
丂傜偡偐傞偝傫丄偁傝偑偲偆偛偞偄傑偡丅偳偺埵偺埵抲偵偁傞偐傪峫偊傑偟偨丅
丂b/a+(d/c -b/a)亊們/(a+c)=(b+d)/(a+c)丂側偺偱丄倶 偲 倷 傪 們 丗 倎丂偵撪暘偡傞揰偱偁傞偙偲
偑暘偐傝傑偟偨丅暘巕偼塭嬁偟側偄偺偑柺敀偄偱偡偹丅
丂倠倱 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾俀擔晅偗乯
丂b/a亙 x/(a亄c) 亙d/c (a亙c)傪枮偨偡 倶 偺昁梫忦審傪挷傋偨傜丄2b亙倶亙2d 偱丄b亄倓 偼丄
傎傏拞娫偱偁傞偙偲偑暘偐傝傑偟偨丅
丂椺偊偽丄3/7亙x/18亙6/11丂偺偲偒丄倶亖7丄8丄9丄10丄11 偱偟偨丅
丂丂丂埲壓丄岺帠拞両




