
「隣り合う分数」の話題の中で、フォードの円なるものが登場した。
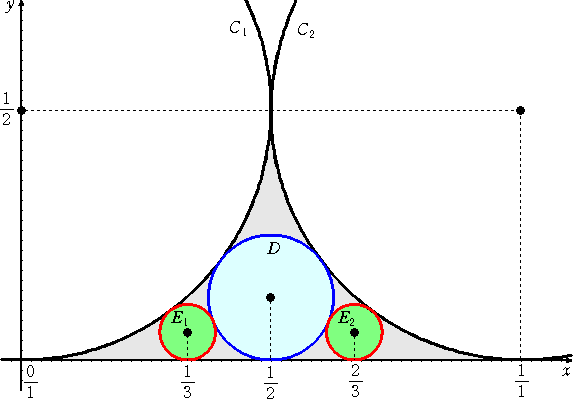
数学において、フォードの円とは、中心が (p/q,1/(2q2)) で、半径が 1/(2q2) の円
のことである。ただし、p/q は既約分数。
フォードの円では、次の公式が基本的である。
フォードの円 
「隣り合う分数」の話題の中で、フォードの円なるものが登場した。

数学において、フォードの円とは、中心が (p/q,1/(2q2)) で、半径が 1/(2q2) の円
のことである。ただし、p/q は既約分数。
フォードの円では、次の公式が基本的である。
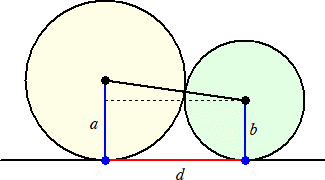 |
半径aの円と半径bの円が外接し、さ らに共通の直線にも接している。 このとき、2接点間の距離dは、次で 与えられる。 |
(証明) 三平方の定理より、 (a−b)2+d2=(a+b)2 なので、 d2=4ab
よって、 ![]() (証終)
(証終)
例 この公式を冒頭の図に適用すると、半径1/2の円と半径1/8の円が外接しているので、
その2接点間の距離dは、 d2=4・(1/2)(1/8)=1/4 より、 d=1/2 となり、確か
に図と合っている。
上記の公式の応用例として次がある。
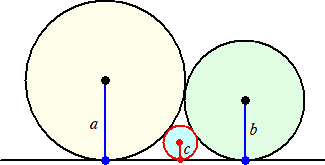 |
半径aの円と半径bの円が外接し、さ らに共通の直線にも接している。 その2つの円と接線に接する半径c の円がある。このとき、 |
(証明) 公式より、 ![]() なので、
なので、
![]()
が成り立つ。 (証終)
例 この公式を冒頭の図に適用すると、半径1/2の円と半径1/8の円に接する円の半径を
c とすると、
1/√c=√2+2√2=3√2
から、 c=1/18 となる。よって、半径1/2の円と半径1/18の円の共通接線上の2接点
間の距離dは、
d2=4・(1/2)(1/18)=1/9 より、 d=1/3 となり、確かに図と合っている。
(追記) 令和3年12月30日付け
上記の公式を問う問題が、お茶の水女子大学前期(2021)で出題された。文理共通問題
で、受験生の学力を見る手頃な問題なのだろう。
お茶の水女子大学前期(2021)
共通の接線 L を持つ円 C1、C2、C3 の半径をそれぞれ a、b、c とする。これらの円
のどの二つも互いに外接しており、C3 は L、C1、C2 に囲まれた領域に含まれているもの
とする。以下の問いに答えよ。
| (1) | |
となることを示せ。 |
(2) c=1 のとき、a+b の取り得る値の最小値を求めよ。
(解)(1)については、上記の(証明)から明らかだろう。
(2)については、相加平均と相乗平均の関係から、 a+b≧2√(ab) なので、a=b のとき、
a+b は最小となる。c=1 で、(1)と a=b から、a=b=4と定まるので、
a+b の最小値は、2√(4・4)=8 である。 (終)
(コメント) 問題の意味するところが理解できれば、三平方の定理を使うだけなので、中学
3年生レベルの問題と言える。お茶の水女子大学受験生の方は完答だったかな。
(追記) 令和7年7月2日付け
次の東北大学 前期理系(1996)の問題は、フォードの円に関する問題である。お茶の水
女子大学前期(2021)の(1)の等式が、解決のポイントである。
(参考) 「隣り合う分数」におけるファレイ数列
問題 xy平面の点(0,1)を中心とする半径1の円をCとし、第1象限にあって x軸とCに接
する円C1を考える。次に、x 軸、C、C1で囲まれた部分にあって、x 軸とこれら2円に接す
る円をC2とする。以下同様に、Cn (n=2、3、・・・)を x 軸、C、Cn-1で囲まれた部分に
あって、これらに接する円とする。
(1) C1の中心の x 座標を a とするとき、C1の半径 r1 を a を用いて表せ。
(2) Cnの半径 rn を a と n を用いて表せ。
(解)(1) (1+r1)2=a2+(r1−1)2 より、 r1=a2/4
(2) 公式より、 1/√rn=1+1/√rn-1 なので、数列{1/√rn}は、初項1/√r1=2/a、
公差1の等差数列である。
よって、 1/√rn=2/a+(n−1)=((n−1)a+2)/a から、
rn=a2/((n−1)a+2)2 (終)
以下、工事中!