
当HPの読者のK.S.さんより、平成23年11月11日付けで標記話題をメールで頂いた。
2次曲線のうち、楕円は、「2定点からの距離の和が一定な点の軌跡」として定義される。
その計算は、多くの教科書、書籍に載っているので省略することにしよう。
2次曲線のうち、双曲線は、「2定点からの距離の差が一定な点の軌跡」として定義される。
その計算は、多くの教科書、書籍に載っているので省略することにしよう。
それでは、「2定点からの距離の商が一定な点の軌跡」として定義される曲線はどんな図形
だろうか。
これについても、高校2年生であれば、数学IIの「図形と方程式」の単元で学ぶアポロニウ
スの円となることはご存じだろう。
すなわち、 PA/PB=m のとき、点Pは線分ABを、m : 1 に内分、外分する点を直径
の両端とする円となる。
2次曲線の放物線、楕円、双曲線は、円錐の切断により得られる。
円錐面 x2+y2−z2=0 と平面 ax+by+cz+d=0 の共有点は、
a=b=0 、z=r のとき、 切断面は 円 となる。
a=c=0 、y=r のとき、 切断面は 双曲線 となる。
a=0 、b=±c のとき、 切断面は 放物線 となる。
a=0 、b≠±c のとき、 切断面は 楕円 となる。
「2定点からの距離」の「和」、「差」、「商」ときて、「積」の場合はどんな図形を表すのだろう
か?
2定点を、A(−c,0)、B(c,0)とし、 AP・BP=a2 (一定) とする。
P(x,y) とすると、条件より、 {(x+c)2+y2}{(x−c)2+y2}=a4
このとき、 (x2−c2)2+2(x2+c2)y2+y4=a4 より、
x4+2x2y2+y4−2c2x2+2c2y2+c4−a4=0
よって、 (x2+y2)2−2c2(x2−y2)+c4−a4=0
ここで、 a=c のとき、レムニスケートとなる。(→ 参考:「連珠形」)
これは、トーラス
(→ 参考「忘れられない先生」)
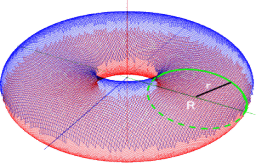
(追記) 令和6年11月13日付け
次の東北大学 理系(1985)の問題は、なかなかよく練られた問題で感心させられる。
問題5 曲線C:x=t+sint 、y=cost−1 上の媒介変数 t (0<t<π)に対応する点をP
とする。
(1) C上の2点O(0,0)とPの間の弧の長さLを求めよ。
(2) PでのCの接線上に点QをPより左側に、PQ=Lとなるようにとる。Qの座標を求めよ。
(3) Pが 0<t<π の範囲で動くとき、Qの描く曲線はCのπ<t<2πの部分と合同になる
ことを証明せよ。
(解)(1) x’=1+cost 、y’=−sint より、(x’)2+(y’)2=2(1+cost)=4cos2(t/2)
このとき、L=2∫0t cos(t/2)dt=4[sin(t/2)]0t=4sin(t/2)
(2) 接線の方向ベクトルは、(1+cost,−sint)
P(x,y)、Q(X,Y)とおくと、 (X−x,Y−y)=k(1+cost,−sint) で、題意より、k<0
(X−x)2+(Y−y)2=2k2(1+cost)=4k2cos2(t/2)=16sin2(t/2) より、
k=−2tan(t/2) である。
よって、 X=t+sint−2tan(t/2)(1+cost)=t+sint−4tan(t/2)cos2(t/2)=t−sint
Y=cost−1+2tan(t/2)sint=cost−1+4sin2(t/2)=cost−1+2(1−cost))=1−cost
以上から、 Q(t−sint,1−cost) となる。
(3) 曲線C:x=t+sint 、y=cost−1 の π<t<2π の部分をKとおく。
t−π=s とおくと、 0<s<π で、
t+sint=π+s+sin(π+s)=π+s−sins
cost−1=cos(π+s)−1=−coss−1
そこで、Kを x 軸方向に −π、y 軸方向に2だけ平行移動すると、
x=s−sins 、y=1−coss となり、これは、点Qが描く図形を表す。
したがって、Pが 0<t<π の範囲で動くとき、Qの描く曲線は、
Cのπ<t<2πの部分と合同になる。 (終)
(コメント) なかなか含蓄のある良問でした。
(追記) 令和7年4月19日付け
次の東北大学 前期文理共通(1992)の問題は、軌跡の基本問題と言える。
問題 短針の長さが1、長針の長さが2の時計がある。短針をa、長針をbとするとき、
点(|a+b|,a・b)の動く範囲を求め、それを図示せよ。ただし、|a+b|はベクト
ルa+bの大きさ、a・bはベクトルaとbの内積を表す。
(解) a、bのなす角をθ(0≦θ≦π)とすると、 a・b=2cosθ
また、|a+b|2=5+4cosθ なので、 x=|a+b|、y=a・b とおくと、
x2=5+2y すなわち、 y=(x2−5)/2
ただし、 −2≦y≦2 で、 x>0 から、 1≦x≦3 である。
以上から、点(|a+b|,a・b)の動く範囲は、y=(x2−5)/2 (1≦x≦3)
求めるグラフは下図。
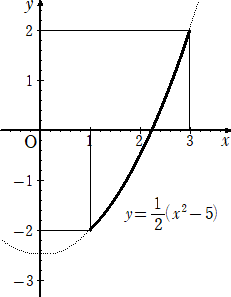
(追記) 令和7年4月20日付け
次の東北大学 前期理系(1992)の問題は、速度に関する問題である。
問題 平面上を運動する点Pの座標(x,y)が、時刻 t の関数として、x=etsint、y=etcost
で与えられている。
(1) 点Pの時刻 t における速度をvとするとき、ベクトルvとOPのなす角θを求めよ。ただし、
Oは原点を表す。
(2) 点Pが描く曲線の時刻 t における接線の傾きをF(t)とするとき、次の積分を求めよ。
∫0π/4 F(t)dt
(解)(1) v=(et(sint+cost),et(cost−sint)) 、OP=(etsint,etcost)より、
v・OP=e2t、|v|=
(2) F(t)=(cost−sint)/(sint+cost) より、
∫0π/4 F(t)dt=[log|sint+cost|]0π/4=log
(追記) 令和7年5月4日付け
次の東北大学 後期文系(1992)の問題は、基本的な軌跡の計算である。
問題 点Aは第1象限に、点Bは第4象限にあり、原点Oを始点とするベクトルOA、OB
が単位ベクトルで、x 軸とのなす角がともにαとする。θが0≦θ≦2πの範囲を動くと
き、OP=cosθOA+sinθOB を位置ベクトルとする点Pが描く図形を求めよ。
(解) OA=(cosα,sinα)、OB=(cosα,−sinα) より、
OP=(cosθcosα+sinθcosα,cosθsinα−sinθsinα)
そこで、 x=cosθcosα+sinθcosα 、y=cosθsinα−sinθsinα とおくと、
x2=cos2α+sin2θcos2α 、y2=sin2α−sin2θsin2α
よって、 (x2−cos2α)/cos2α+(y2−sin2α)/sin2α=0 より、
x2/cos2α+y2/sin2α=2 即ち、 x2/(2cos2α)+y2/(2sin2α)=1
これは、2定点A、Bを通る楕円で、長軸、短軸が各座標軸となる。 (終)
(追記) 令和7年8月22日付け
次の東北大学 前期理系(1998)の問題は、2次曲線の定義に関わる問題である。
問題 (1) 点P(p,q)と円C:(x−a)2+(y−b)2=r2 (r>0)との距離dとは、PとC上の
点(x,y)との距離の最小値をいう。PがCの外部にある場合と内部にある場合に分けて、
dを表す式を求めよ。
(2) 2つの円C1:(x+4)2+y2=81とC2:(x−4)2+y2=49から等距離にある点Pの
軌跡の方程式を求めよ。
(解)(1) PがCの外部にある場合、 d=√{(p−a)2+(q−b)2}−r
PがCの内部にある場合、 d=r−√{(p−a)2+(q−b)2}
(2) PがC1の外部、C2の外部にある場合、
√{(p+4)2+q2}−9=√{(p−4)2+q2}−7
PがC1の外部、C2の内部にある場合、
√{(p+4)2+q2}−9=7−√{(p−4)2+q2}
PがC1の内部、C2の外部にある場合、
9−√{(p+4)2+q2}=√{(p−4)2+q2}−7
PがC1の内部、C2の内部にある場合、
9−√{(p+4)2+q2}=7−√{(p−4)2+q2}
以上から、 √{(p+4)2+q2}=√{(p−4)2+q2}+2
または、 √{(p+4)2+q2}=−√{(p−4)2+q2}+16
まず、 √{(p+4)2+q2}=√{(p−4)2+q2}+2 の両辺を平方して整理すると、
4p−1=√{(p−4)2+q2}
4p−1≧0 すなわち、 p≧1/4 に注意して、両辺を平方して整理すると、
15p2−q2=15 すなわち、 x2−y2/15=1 (x>0)
次に、 √{(p+4)2+q2}=−√{(p−4)2+q2}+16 の両辺を平方して整理すると、
p−16=−2√{(p−4)2+q2}
p−16≦0 すなわち、 p≦16 に注意して、両辺を平方して整理すると、
3p2+4q2=192 すなわち、 x2/64+y2/48=1 (終)
(コメント) √{(p+4)2+q2}+√{(p−4)2+q2}=16 から、2定点(−4,0)、(4,0)
からの距離の和が16であるので、楕円となる。
楕円の方程式 x2/a2+y2/b2=1 において、a>b>0 で、a2−b2=16 、2a=16
から、 a=8 となり、 b2=64−16=48 よって、 x2/64+y2/48=1 となる。
(追記) 令和7年12月3日付け
次の東北大学 後期理系(2003)の問題は、基本的な問題だろう。
問題 平面において、点P(s,t)は原点Oを中心とする半径1の円周上にあり、点Q(u,v)
は点(1,0)を中心とする半径1の円周上にある。PとQがPQ=1を保ちながら動くとき、
次の問いに答えよ。
(1) s≠1 のとき、u、v を s と t の式で表せ。
(2) 線分PQの中点の軌跡を図示せよ。
(解)(1) 題意より、 s2+t2=1 、(u−1)2+v2=1 、(s−u)2+(t−v)2=1
このとき、 v2=2u−u2 なので、 s2−2su+u2+t2−2tv+2u−u2=1
すなわち、 −2su−2tv+2u=0 より、 u(1−s)=tv
両辺を平方して、 u2(1−s)2=t2v2=t2(2u−u2) より、
u2{(1−s)2+t2}=2t2u すなわち、 2u2(1−s)=2(1−s2)u において、
s≠1 より、 u2−(1+s)u=0 よって、 u=0 または u=1+s
u=1+s のとき、 tv=1−s2=t2 から、 t=0 または v=t
ここで、 u=0 のとき、v=0 で、 s=−1、t=0 とおけばよいので、
一般に、s≠1 のとき、 u=1+s 、v=t と書ける。
(2) PQの中点をM(x,y)とおくと、s≠1 のとき、 u=1+s 、v=t から、
x=(s+u)/2=(2s+1)/2 、y=(t+v)/2=t より、
(2x−1)2/4+y2=1 から、 (x−1/2)2+y2=1
ただし、 u≠0 、s≠1 から、(−1/2,0)、(3/2,0) は除く。
u=0 のとき、v=0 で、Q(0,0)から、線分PQの中点Mの軌跡は、x2+y2=1/4
ただし、(−1/2,0)も含む。
s=1 のとき、t=0 で、P(1,0)から、線分PQの中点Mの軌跡は、(x−1)2+y2=1/4
ただし、(3/2,0)も含む。
以上から、求める軌跡は下図の通りである。

以下、工事中!