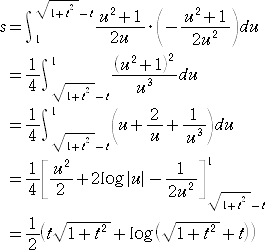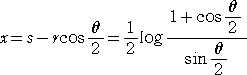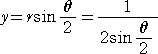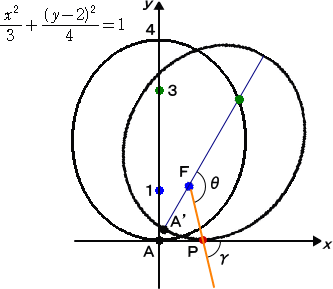ドローネー曲線　 　　　　　　　　　　　　　　　　　

　平成１７年５月２８日　Ｌｉｃｈｔ さんという方から当ＨＰの掲示板「出会いの泉」に質問が寄
せられた。

　　「放物線が定直線上をすべることなく転がるとき、その焦点が描く軌跡はカテナリー（懸垂線）で
　ある」ということを知り、なんとか証明することができた。その後、「楕円が定直線上をすべることな
　く転がるとき、その焦点が描く軌跡」、「双曲線が定直線上をすべることなく転がるとき、その焦点
　が描く軌跡」にもそれぞれ「アンデュラリー」、「ノーダリー」という名前がついていることを知り、そ
　の方程式を求めようとしたのだが、楕円の弧長を求めるには大学以上の知識が必要であるらしく、
　高校３年の私にとっては、その後進展しなかった。しかし、せめてその方程式や概形が知りたいと
　いう思いはある。どなたか、よろしくお願い致します。

　これに対して、よこやまさんという方から情報が寄せられた。

　　Ｌｉｃｈｔ さんの軌跡の問題ですが、Ｇｏｏｇｌｅ 検索してみたら、「転がる石に苔むさず」というＨＰが
　ありました。曲面論とか微分幾何学の本を探せば、どれかに書いてある内容だと思います。（例え
　ば、「曲面と曲線ー微分幾何的アプローチ」（梅原・山田(著)；掌華房）など）或いは、まだ調べてい
　ませんが、岩波数学辞典とかにあるかも知れません。

　そこで、よこやまさんから提示された岩波数学辞典を調べてみた。

　第２版の４４１ページに、楕円または双曲線が定直線上を転がるときの焦点の軌跡は、
Ｄｅｌａｕｎａｙの曲線として紹介されていて、しかも、それらしい図も載っていた！

　外国の文献まで検索すると、次のＨＰがそれなりに詳しいように思う。

　　　Delaunay's roulette

　そこで、このページでは、Ｌｉｃｈｔ さんに刺激されて、輪転曲線（Ｄｅｌａｕｎａｙ’ｓ　ｒｏｕｌｅｔｔｅ）
について、いろいろ整理しようと思う。

　定曲線上を他の曲線が滑らずに転がるとき、転がる曲線に固定された点が描く軌跡を
求める（＝roulette　という）問題は数学的にも興味があり、また応用上も重要な意味を持
つ。

　このような曲線として、当ＨＰでは、いくつかの例を紹介してきた。

たとえば、　擺線　、餘擺線　、外サイクロイド　、内サイクロイド　など．．．。

　特に、定直線上を２次曲線が転がるときの軌跡を、

　　　　　　　Ｄｅｌａｕｎａｙ’ｓ　ｒｏｕｌｅｔｔｅ　（輪転曲線）

というようだ。

　この曲線については、Ｄｅｌａｕｎａｙ（1816〜1872）が １８４１年に初めて取り上げたらしい。

　この曲線の解析のためには、直交座標系よりも極座標系で議論する方が美しく簡潔に
表現される。　まずは、予備知識の確認から始めよう！

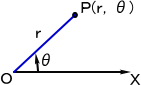　　　極座標は、平面上の定点 Ｏ と Ｏ から出る半直線 ＯＸ から
　　なる。　平面上の点 Ｐ に対して、
　　　　ＯＰ＝ｒ　、∠ＸＯＰ＝θ　（ＯＸから反時計回りに測った角）
　　のとき、（ｒ ，θ） を、点Ｐの極座標といい、Ｐ（ｒ ，θ） と書く。
　　

　このとき、　Ｏ を極座標の極、半直線 ＯＸ を始線、ＯＰ を動径、θ を偏角という。

　極座標においては、ｒ＜０ ということもあり得る。

（ｒ ，θ）に対して、極Ｏと点対称な点 （ｒ ，θ＋π） を、（−ｒ ，θ） と表現する。

例　極座標（−１，π/４）が表す点は、極座標（１，π/４）が表す点を極の周りに１８０°回
　　転させた点である。したがって、（１，５π/４）と同じ意味である。


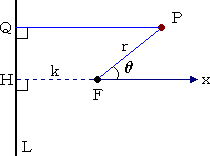
２次曲線の統一的定義

　２次曲線は、定点Ｆと、点Ｆを通らない定直線Ｌからの距離の比が一定な点Ｐの軌跡と
定義される。

　今、点Ｆから直線Ｌに下ろした垂線の足をＨとし、その垂線の長さ（ＦＨ）を、ｋ とおく。右
下図のように、Ｆを極とし、ＨＦの方向に始線を定める。

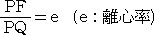
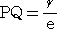
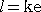
点Ｐより直線Ｌに下ろした垂線の足をＱとするとき、 定義より、 　　　　　　　　 である。 　右図より、　ＰＱ＝ｋ＋ｒｃｏｓθ　なので、この式に、 　　　　　　　　 　　　　　　　　　　 を代入して整理すれば、次のような極方程式が得ら れる。

　　　　　

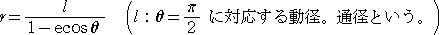
ここで、０＜ｅ＜１ のとき、楕円、ｅ＝１ のとき、放物線、ｅ＞１ のとき、双曲線を表す。

　また、定点Ｆを焦点、定直線Ｌを準線という。

　準線は、放物線に限らず、楕円や双曲線にも存在する。

　また、下図のように、曲線 ｒ＝Ｆ(θ) 上の１点 Ｐ(ｒ，θ) における接線と始線のなす角を α 、
動径とのなす角を β とすると、次の式が成り立つ。

　　　　

　　　　

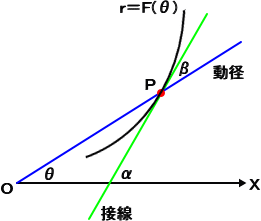
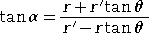
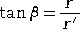
　　　実際に、前半は、
　　　　　　　　　　　　　

　　　から明らか。
　　　　後半は、β＝α−θ と、加法定理から容易に
　　　導かれる。

　以上の準備をもとにして、いよいよ本論に入ろう。

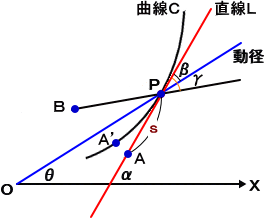
　今、定直線 Ｌ 上を２次曲線 Ｃ が滑らずに転がるものとする。直線 Ｌ 上の一点 Ａ から接
点 Ｐ までの長さと曲線 Ｃ 上の一点 Ａ’ から接点 Ｐ までの曲線に沿う長さは等しく、その
値を ｓ とおく。

　点 Ｏ を極座標系の極（原点）とし、動径 ＯＰ の長さを ｒ 、始線 ＯＸ から反時計回りに測っ
た角を θ とする。

　また、点 Ｐ において、直線 ＯＰ から直線 Ｌ まで反時計回りに測った角を β とする。

そして、曲線 Ｃ に固定された点 Ｂ と点 Ｐ の距離を Ｒ とし、直線 ＢＰ から直線 Ｌ まで反時
計回りに測った角を γ とする。（下図参照）

　　　　このとき、
　　　　　　　　　　　　

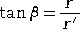
　　　　により、
　　　　　　　　　　　　

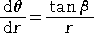
　　　　なので、
　　　　　　　　　　　　



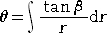
　（これより、 β 、 ｒ は、ｓ の関数なので、θ も ｓ の関数である。←当たり前かな！？）

　上図から、ベクトル ＯＰ は、複素数 ｒ・ｅｘｐ（ｉθ） で表される。　また、直線 ＢＰ が始線
ＯＸ となす角は、θ＋β−γ なので、ベクトル ＰＢ は、

　　　　　　　　　複素数　−Ｒ・ｅｘｐ（ｉ（θ＋β−γ））

で表される。したがって、ベクトル ＯＢ は、

　　　　　　　　　複素数　ｒ・ｅｘｐ（ｉθ）−Ｒ・ｅｘｐ（ｉ（θ＋β−γ））

で表される。　したがって、点 Ｂ の直交座標を、（ ｘ ， ｙ ） とおくと、

　　　　　ｘ ＝ ｒ・ｃｏｓθ−Ｒ・ｃｏｓ（θ＋β−γ）

　 　　　 ｙ ＝ ｒ・ｓｉｎθ−Ｒ・ｓｉｎ（θ＋β−γ）

　これが、Ｄｅｌａｕｎａｙ’ｓ　ｒｏｕｌｅｔｔｅ（輪転曲線） を表す方程式の一般形である。

　後は、具体的な曲線 Ｃ の性質により、　ｒ 、Ｒ、θ、β、γ　を決定し、軌跡の方程式を求め
ればよい。

　特に、定直線 Ｌ が始線 ＯＸ と重なり、点 Ａ が点 Ｏ と一致するときが通常の初期設定
になるだろう。

　このとき、　θ＝０　、ｒ ＝ ｓ　、β＝０　なので、上記の媒介変数表示は、

　　　　　ｘ ＝ ｓ−Ｒ・ｃｏｓγ　、　 ｙ ＝ Ｒ・ｓｉｎγ

となる。（この方程式は、下記の例の図とにらめっこをすると、当たり前の式だろう！）

例　曲線 Ｃ を、半径 ｒ の円とし、その周上の固定された点を Ｂ とする。いま、Ｂは原点に
　一致しているものとする。ｘ 軸上を円が滑らずに転がるとき、その点 Ｂ の軌跡の方程式
　を求めてみよう。

　　　　　　　　　　　

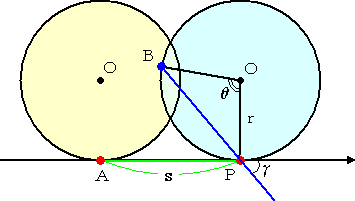
　図より、Ｒ＝２ｒ・ｓｉｎ(θ/２) 、ｓ ＝ ｒ・θ 、γ＝ θ/２　なので、上記の公式に代入すると、

　　ｘ ＝ ｒ・θ−２ｒ・ｓｉｎ(θ/２)ｃｏｓ(θ/２) ＝ ｒ・θ− ｒ・ｓｉｎθ＝ ｒ・（θ− ｓｉｎθ）

　　ｙ ＝ ２ｒ・ｓｉｎ(θ/２)・ｓｉｎ(θ/２) ＝ ２ｒ・ｓｉｎ²(θ/２) ＝ ｒ・（１− ｃｏｓθ）

となる。これは、よく見慣れたサイクロイドの曲線の方程式である。

（コメント）　上記の曲線の方程式の求め方は通常のものと若干異なる。このような求め方
　　　　　　もあるのだなと今更ながら感心してしまう。（参考 →　擺線　）

例　曲線 Ｃ を、放物線 ｘ²＝２ｙ　とし、曲線 Ｃ に固定された点 Ｂ として、焦点 Ｆ を考える。
　　放物線が ｘ 軸上を滑らずに転がるとき、焦点 Ｆ の軌跡の方程式を求めてみよう。

　　　　　　　　　

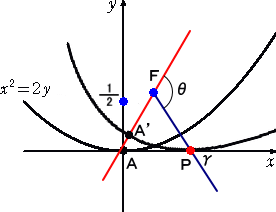
　いま、焦点 Ｆ を極とし、直線Ａ’Ｆを始線とする。このとき、放物線の極方程式は、

　　　　　　　　　　　　　

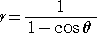
である。また、放物線と接線の性質（→　参考　放物線）から、　γ＝θ/２　が成り立つ。

　焦点 Ｆ の座標を、（ ｘ ， ｙ ） とおくと、公式より、

　　　ｘ ＝ ｓ − ｒ・ｃｏｓ（θ/２）　、　ｙ ＝ ｒ・ｓｉｎ（θ/２）

と書ける。ここで、ｓ は、線分ＡＰの長さに等しい。

ｔ ＝ ｒ・ｓｉｎθ　として、ｓ の値を求めてみよう。　ｘ²＝２ｙ　より、　ｙ’＝ ｘ　なので、

　　　

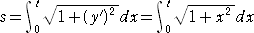
　ここで、　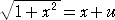　と変数変換して、

　　　　　、　　、　

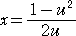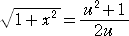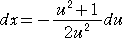
である。　これらを上記に代入して、

　　　

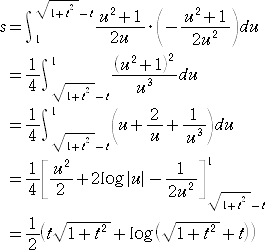
を得る。　ここで、
　　　　
なので、
　　　　　
と書ける。

　したがって、焦点 Ｆ の座標 （ ｘ ， ｙ ） について、
　　　　　
　　　　　
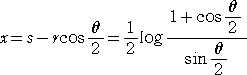
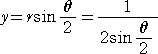
が成り立つ。

　この２式より、θ を消去すれば、ｘ 、ｙ の関係式が得られる。

　　　　　、　

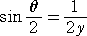なので、
　　　　　　　

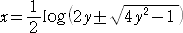
となる。　この式を、ｙ について解けば、

　　　　　　　
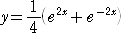
　ここで、　
　　　　　　　
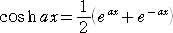
なので、
　　　　　　　

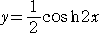
とも書ける。　これは、懸垂線の方程式である。

（コメント）　上記において、煩雑な計算を避けるために、放物線の方程式として、ｘ²＝２ｙ
　　　　　　としたが、一般の放物線 ｘ²＝４ｐｙ　についても同様の計算を行えば、同様の結
　　　　　　果が得られる。高校３年のＬｉｃｈｔ さんは、どんな風に計算されたのだろうか？

（追記）　Ｌｉｃｈｔ さんから上記の問題の計算についてメールを頂いた。（平成１７年６月６日付け）
　　　　　また、快く当ＨＰへの掲載をご承諾いただいたので、下記に若干の計算を補足して
　　　　　Ｌｉｃｈｔ さんの解答を示したいと思う。

　座標軸の原点を Ａ 、放物線を　ｘ² ＝ ４ｐｙ　（ ｐ＞０ ）、焦点を、Ｆ（ ０ ， ｐ ） とする。

　まず、放物線上の点Ｐ( ｔ ， ｔ²/４ｐ )　について、ｔ の増加する方向を正とした放物線上の
弧 ＡＰ の符号付き長さ ｓ を求める。

　　　　　　
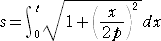
ここで、
　　　　　　　

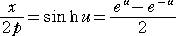
と変数変換して、
　　　　　　　　　
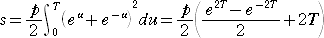
ただし、
　　　　　　　
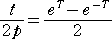
である。
　このとき、
　　　　　　　　　、　

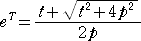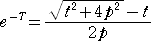
を上式に代入して整理すると、

　　　　　　　　　　　
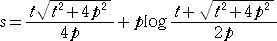
となる。

　次に、点Ｐにおける放物線の接線方向ベクトル （ ２ｐ ， ｔ ） と
ベクトルＦＰ ＝ ( ｔ ， −ｐ＋ｔ²/４ｐ ) のなす角を γ （ ０＜γ＜π ）とし、ｃｏｓγ と ｓｉｎγ を求める。

　二つのベクトルの内積と絶対値から、

　　　　　　　　　、　
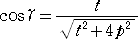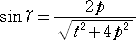
が成り立つ。

　　　　　　　　　　

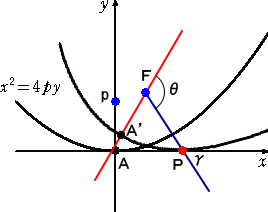
　放物線が点Ｐまで転がるとき、点Ｐの座標は、Ｐ( ｓ ， ０ )であり、そのときの焦点 Ｆ の座
標を、Ｆ（ ｘ ， ｙ ） とおけば、

　　　　　　 ｘ ＝ ｓ−|ＰＦ|ｃｏｓγ　　、　ｙ ＝ |ＰＦ|ｓｉｎγ

となる。　これらに上記で得られた式を代入して、

　　　　　　　、　
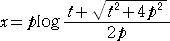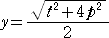
を得る。

　これらから、ｔ を消去して
　　　　　　　　　　　　　　　　　　

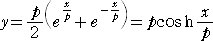
という結果を得る。

（コメント）　Ｌｉｃｈｔ さんの解答は、私の解答と大体同じですね！一般の場合の証明に挑戦
　　　　　　されたことに脱帽です。Ｌｉｃｈｔ さんの解答では、置換積分における置換の方法が
　　　　　　斬新ですね。私自身気がつきませんでした。Ｌｉｃｈｔ さんによれば、初めの方の計
　　　　　　算が煩雑で、Ｂ４の紙が埋まるほど大変だったそうです。また、ｃｏｓθ と ｓｉｎθを求
　　　　　　めるとき、図形的な問題を機械的な計算に帰着できるベクトルの威力というもの
　　　　　　を再認識されたそうです。
　　　　　　　どんな図形も弧長と微分係数さえ分かれば、直線上を転がるときの軌跡が求
　　　　　　められそうかなと思ったが、楕円の弧長が具体的に求められないことを知って、
　　　　　　何とも残念なことですと、Ｌｉｃｈｔ さんは感想を述べられていました。

例　曲線 Ｃ を、楕円とし、曲線 Ｃ に固定された点 Ｂ として、焦点 Ｆ を考える。
　　楕円が ｘ 軸上を滑らずに転がるとき、焦点 Ｆ の軌跡を考えてみよう。

　　　　　　

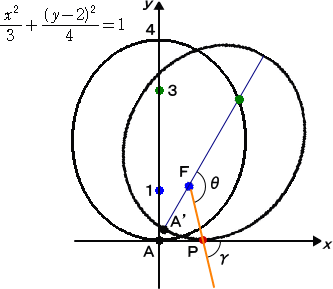
　焦点 Ｆ の座標 （ ｘ ， ｙ ） について、

　　　　ｘ ＝ ｓ−Ｒ・ｃｏｓγ　、　 ｙ ＝ Ｒ・ｓｉｎγ

が成り立つ。

　楕円の弧長は、簡単な形に表すことができないので、これ以上話は進展しない。

楕円を少し転がし続けると、下図のような赤い点線の軌跡を描く。

　　　　　　　

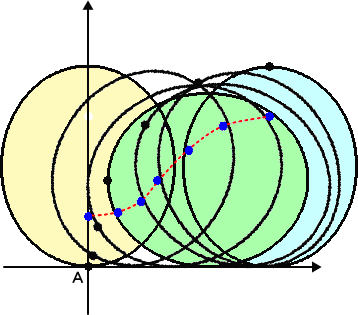
　したがって、焦点 Ｆ の軌跡は下図のようになる。



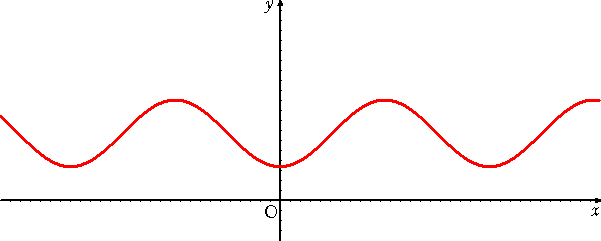
　この曲線のことを、「アンデュラリー」というそうである。このようなグラフが岩波数学辞典
に掲載されている。