内接円と傍接円　 　　 　　　　　　　　　　　　　　　　　　　

　いくつかの特殊な三角形について、その内接円の半径や傍接円の半径を求めてみよう。

（１）　ＡＢ＝２、ＢＣ＝、ＣＡ＝１の直角三角形ＡＢＣの場合

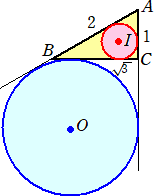内接円の半径を ｒ とおくと、　（１＋ｒ）＋ｒ＝　より、 　　　　ｒ＝（−１）/２ 　　傍接円の半径を Ｒ とおくと、　Ｒ/（−Ｒ）＝ｔａｎ７５° 　　ここで、ｔａｎ７５°＝２＋　なので、Ｒ/（−Ｒ）＝２＋ 　　よって、　Ｒ＝（＋１）/２

（２）　１辺の長さが２の正三角形ＡＢＣの場合

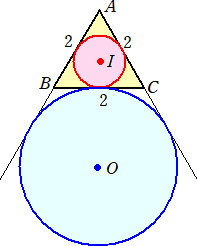内接円の半径を ｒ とおくと、３ｒ ＝　より、ｒ ＝１/ 　　（ ｒ ＝ｔａｎ３０°から、ｒ＝１/　としてもよい） 　　傍接円の半径を Ｒ とおくと、　Ｒ＝ｔａｎ６０°＝

　上記（１）（２）において、傍接円の半径 Ｒ は何れも正接の三角比を用いたが、次の公式
を用いてもよい。（→　参考：「三角形の面積の公式」）

　△ＡＢＣ　において、ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ　とし、ｓ＝（ａ＋ｂ＋ｃ）/２　とする。

　このとき、傍接円の半径 Ｒ は、

　　　Ｒ＝（ｓ−ｂ）（ｓ−ｃ）/ｒ　（ ｒ は内接円の半径）

で与えられる。

　この公式を用いれば、

（１）は、　ｓ＝（３＋）/２　より、Ｒ＝（ｓ−１）（ｓ−２）/ｒ＝（＋１）/２

（２）は、　ｓ＝３　より、Ｒ＝（ｓ−２）（ｓ−２）/ｒ＝

と求められる。


　この公式を用いて、新たな深淵に立ち入ろうと思う。まずは、その準備である。

　ＡＢ＝２、ＢＣ＝、ＣＡ＝１の直角三角形ＡＢＣにおいて、∠Ａの２等分線を考え、辺ＢＣ
との交点をＤとおく。

　

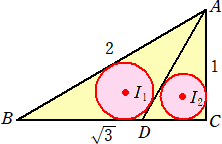
　このとき、

　　ＣＤ＝１/　、ＢＤ＝−１/＝２/　、ＡＤ＝２/

であることは明らかだろう。

　△ＡＢＤ、△ＡＤＣの内接円 Ｉ₁、Ｉ₂ の半径をそれぞれ ｒ₁、ｒ₂ とおく。

　△ＡＢＤ＝（１/２）・２・（２/）・（１/２）＝１/

　△ＡＤＣ＝（１/２）・（１/）・１＝１/（２）

なので、　（１/２）・（２＋２/＋２/）・ｒ₁＝１/　より、　ｒ₁＝２−

　（１/２）・（１＋２/＋１/）・ｒ₂＝１/（２）　より、　ｒ₂＝１/（３＋）

　また、△ＡＢＤ、△ＡＤＣの傍接円の半径をそれぞれ Ｒ₁、Ｒ₂ とおく。

　△ＡＢＤにおいて、　ｓ₁＝（２＋２/＋２/）/２＝（３＋２）/３　より、

　Ｒ₁＝（ｓ₁−２/）（ｓ₁−２）/ｒ₁＝１/

同様に、△ＡＤＣにおいて、　ｓ₂＝（１/＋１＋２/）/２＝（１＋）/２　より、

　Ｒ₂＝（ｓ₂−１）（ｓ₂−２/）/ｒ₂＝（−１）/２

ここで、

　ｒ₁/Ｒ₁＝（２−）・＝２−３

　ｒ₂/Ｒ₂＝１/（３＋）・２/（−１）＝１/

が成り立つ。

よって、　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）＝２−　である。

ところで、　ｒ/Ｒ＝（−１）/２・２/（＋１）＝２−　であるので、

　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）＝ｒ/Ｒ

が成り立つ。


（コメント）　これは、美しい関係式ですね！（２）でも成り立つかどうか確かめてみよう。

　１辺の長さが２の正三角形ＡＢＣにおいて、∠Ａの２等分線を考え、辺ＢＣとの交点をＤとお
く。
　

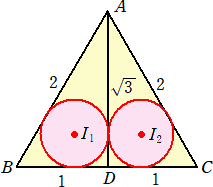
　このとき、　ＢＤ＝ＣＤ＝１　、ＡＤ＝　であることは明らかだろう。

　△ＡＢＤ、△ＡＤＣの内接円 Ｉ₁、Ｉ₂ の半径をそれぞれ ｒ₁、ｒ₂ とおく。

　△ＡＢＤ＝△ＡＤＣ＝（１/２）・１・＝/２　なので、

　（１/２）・（２＋１＋）・ｒ₁＝/２　より、　ｒ₁＝１/（＋１）　、ｒ₂＝１/（＋１）

また、△ＡＢＤ、△ＡＤＣの傍接円の半径をそれぞれ Ｒ₁、Ｒ₂ とおく。

△ＡＢＤにおいて、　ｓ₁＝（２＋１＋）/２＝（３＋）/２　より、

　Ｒ₁＝（ｓ₁−）（ｓ₁−２）/ｒ₁＝（３−）/２　、Ｒ₂＝（３−）/２

ここで、　ｒ₁/Ｒ₁＝１/（＋１）・２/（３−）＝１/　、ｒ₂/Ｒ₂＝１/　が成り立つ。

よって、　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）＝１/３　である。

ところで、　ｒ/Ｒ＝１/・１/＝１/３　であるので、

　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）＝ｒ/Ｒ

が成り立つ。


（コメント）　やはり、この場合も　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）＝ｒ/Ｒ　が成り立ちましたね！


　今度は、３等分の場合も成り立つかどうか確認してみよう。

　１辺の長さが２の正三角形ＡＢＣにおいて、∠Ａの３等分線を考え、辺ＢＣとの交点をＤ、Ｅ
とおく。
　

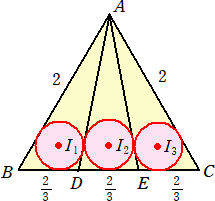
このとき、　ＢＤ＝ＤＥ＝ＥＣ＝２/３　で、余弦定理より、

　ＡＤ²＝２²＋（２/３）²−２・２・（２/３）・（１/２）＝２８/９

よって、ＡＤ＝２/３　である。また、ＡＥ＝２/３　である。

　△ＡＢＤ、△ＡＤＥ、△ＡＥＣ の内接円 Ｉ₁、Ｉ₂、Ｉ₃ の半径をそれぞれ ｒ₁、ｒ₂、ｒ₃ とおく。

　△ＡＢＤ＝△ＡＥＣ＝（１/２）・２・（２/３）・（/２）＝１/　なので、

　（１/２）・（２＋２/３＋２/３）・ｒ₁＝１/　より、ｒ₁＝/（４＋）、ｒ₃＝/（４＋）

　△ＡＤＥ＝（１/２）・（２/３）・＝１/　なので、

　（１/２）・（２/３＋２/３＋２/３）・ｒ₂＝１/　より、　ｒ₂＝/（２＋１）

また、△ＡＢＤ、△ＡＤＥ、△ＡＥＣ の傍接円の半径をそれぞれ Ｒ₁、Ｒ₂、Ｒ₃ とおく。

　△ＡＢＤにおいて、　ｓ₁＝（２＋２/３＋２/３）/２＝（４＋）/３　より、

　Ｒ₁＝（ｓ₁−２/３）（ｓ₁−２）/ｒ₁＝（−２）/　、Ｒ₃＝（−２）/

　△ＡＤＥにおいて、　ｓ₂＝（２/３＋２/３＋２/３）/２＝（２＋１）/３　より、

　Ｒ₂＝（ｓ₂−２/３）（ｓ₂−２/３）/ｒ₂＝（２＋１）/（９）

ここで、

　ｒ₁/Ｒ₁＝/（４＋）・/（−２）＝３/（２−１）　、ｒ₃/Ｒ₃＝３/（２−１）

　ｒ₂/Ｒ₂＝/（２＋１）・９/（２＋１）＝２７/（２＋１）²

が成り立つ。よって、

　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）（ｒ₃/Ｒ₃）＝３/（２−１）・２７/（２＋１）²・３/（２−１）＝１/３

である。

　ところで、　ｒ/Ｒ＝１/・１/＝１/３　であるので、

　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）（ｒ₃/Ｒ₃）＝ｒ/Ｒ

が成り立つ。


　上記においては特別な三角形、特別な場合について見てきたが、実は、これまでの性質
は、一般の△ＡＢＣにおいても成り立つようだ。すなわち、

　頂角Ａを通る ｎ−１個の線分ＡＤ₁、ＡＤ₂、・・・、ＡＤ_n-1により、初めの三角形は

ｎ 個の三角形△ＡＢＤ₁、△ＡＤ₁Ｄ₂、・・・、△ＡＤ_n-1Ｃに分割される。

　これらの三角形の内接円の半径、傍接円の半径をそれぞれ ｒ₁、ｒ₂、・・・、ｒ_n 及び

Ｒ₁、Ｒ₂、・・・、Ｒ_n とおき、△ＡＢＣの内接円の半径、傍接円の半径をそれぞれ ｒ 、Ｒ

とおくとき、　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）・・・（ｒ_n/Ｒ_n）＝ｒ/Ｒ　が成り立つ。


　証明のために、いくつか準備をしよう。

　 △ＡＢＣ において、ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ とし、２ｓ＝ａ＋ｂ＋ｃ　により、ｓ を定める。

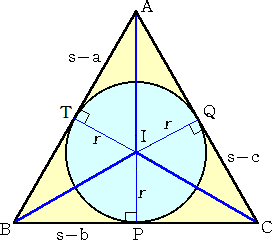△ＡＢＣ の内心を Ｉ　、半径を ｒ とし、Ｉ から各 　辺に下ろした垂線の足をそれぞれ Ｐ、Ｑ、Ｔ　と 　する。 　　△ＡＢＣ＝ｓｒ　である。 　　また、△ＡＢＣ の傍接円の中心をＯ、半径をＲ 　とする。 　　１つの頂点から引いた接線の長さは等しいか 　ら、ＢＰ＋ＣＱ＋ＡＴ＝ｓ　が成り立つ。

このとき、ＢＰ＝ｓ−ＣＱ−ＡＴ＝ｓ−ＣＱ−ＡＱ＝ｓ−ＣＡ＝ｓ−ｂ

　ＣＱ＝ｓ−ＢＰ−ＡＴ＝ｓ−ＢＴ−ＡＴ＝ｓ−ＡＢ＝ｓ−ｃ　である。

　面積について、　△ＡＢＣ＝△ＯＡＢ＋△ＯＣＡ−△ＯＢＣ＝（ｂ＋ｃ−ａ）Ｒ/２＝（ｓ−ａ）Ｒ

なので、　ｒ/Ｒ＝（ｓ−ａ）/ｓ　が成り立つ。

　また、△ＢＰＩ において、

ｔａｎ（Ｂ/２）＝ｒ/（ｓ−ｂ）＝/（ｓ（ｓ−ｂ））＝√[（ｓ−ａ）（ｓ−ｃ）/（ｓ（ｓ−ｂ））]

ｔａｎ（Ｃ/２）＝ｒ/（ｓ−ｃ）＝/（ｓ（ｓ−ｃ））＝√[（ｓ−ａ）（ｓ−ｂ）/（ｓ（ｓ−ｃ））]

なので、　ｔａｎ（Ｂ/２）ｔａｎ（Ｃ/２）＝（ｓ−ａ）/ｓ＝ｒ/Ｒ　が成り立つ。


　さて、準備が出来たので、証明に入ろう。証明は、数学的帰納法による。

（証明）　ｎ＝１ のときは、自明である。

　ｎ＝２ のとき、ＢＣ上の分点をＤとおくと、

　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）

＝ｔａｎ（Ｂ/２）ｔａｎ（∠ＡＤＢ/２）ｔａｎ（∠ＡＤＣ/２）ｔａｎ（Ｃ/２）

＝ｔａｎ（Ｂ/２）ｔａｎ（∠ＡＤＢ/２）ｃｏｔ（∠ＡＤＢ/２）ｔａｎ（Ｃ/２）

＝ｔａｎ（Ｂ/２）ｔａｎ（Ｃ/２）

＝ｒ/Ｒ

なので、命題は、ｎ＝２のとき、成り立つ。

　ｎ−１個の三角形に対して、命題が成り立つと仮定する。

　△ＡＢＤ₂ の内接円、傍接円の半径をそれぞれ ｒ₁₂、Ｒ₁₂ とすると、

　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）＝ｒ₁₂/Ｒ₁₂

である。帰納法の仮定から、　（ｒ₁₂/Ｒ₁₂）（ｒ₃/Ｒ₃）・・・（ｒ_n/Ｒ_n）＝ｒ/Ｒ　が成り立つ。

よって、　（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）（ｒ₃/Ｒ₃）・・・（ｒ_n/Ｒ_n）＝ｒ/Ｒ　が成り立ち、ｎ個の三角形につい
てもなりたつことが示された。

以上から、全ての自然数 ｎ に対して、

（ｒ₁/Ｒ₁）（ｒ₂/Ｒ₂）（ｒ₃/Ｒ₃）・・・（ｒ_n/Ｒ_n）＝ｒ/Ｒ

が成り立つ。　　（証終）


（追記）　令和４年１月２３日付け

　△ＡＢＣ において、ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ とし、２ｓ＝ａ＋ｂ＋ｃ　により、ｓ を定める。

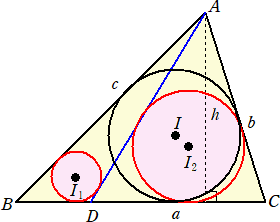△ＡＢＣ の内心を Ｉ　、半径を ｒ とすると、 　△ＡＢＣ＝ｓｒ　である。 　　また、△ＡＢＤ、△ＡＤＣの内心をそれぞれ 　 Ｉ1、Ｉ2 とし、その半径をそれぞれ ｒ1、ｒ2 と 　おく。 　　また、△ＡＢＣの底辺ＢＣに頂点Ａより下ろ 　した垂線の長さを ｈ とおく。

　このとき、　１−２ｒ/ｈ＝（１−２ｒ₁/ｈ）（１−２ｒ₂/ｈ）　が成り立つ。

（証明）　Ｉ、Ｉ₂ より辺ＢＣに下ろした垂線の足をＨ、Ｈ₂ とすると、Ｃ、Ｉ₂、Ｉ は同一直線上にあ
　　　　るので、

　ｒ₂/ＣＨ₂＝ｒ/ＣＨ　すなわち、　ＣＨ₂＝（ｒ₂/ｒ）ＣＨ　が成り立つ。

ここで、　ＣＨ＝ｓ−ｃ　なので、　ＣＨ₂＝（ｒ₂/ｒ）（ｓ−ｃ）　となる。

このとき、

△ＡＢＤ＝（１/２）ＡＢ・ｒ₁＋（１/２）ＢＤ・ｒ₁＋（１/２）（ＣＤ−ＣＨ₂）・ｒ₁＋（１/２）（ＡＣ−ＣＨ₂）・ｒ₁

　＝（１/２）（ＡＢ＋ＢＣ＋ＣＡ）・ｒ₁−ＣＨ₂・ｒ₁＝ｓｒ₁−（ｒ₁ｒ₂/ｒ）（ｓ−ｃ）＝ｒ₁（ｓ−（ｒ₂/ｒ）（ｓ−ｃ））

同様にして、

　Ｉ、Ｉ₁ より辺ＢＣに下ろした垂線の足をＨ、Ｈ₁ とすると、Ｂ、Ｉ₁、Ｉ は同一直線上にあるので、

　ｒ₁/ＢＨ₁＝ｒ/ＢＨ　すなわち、　ＢＨ₁＝（ｒ₁/ｒ）ＢＨ　が成り立つ。

ここで、　ＢＨ＝ｓ−ｂ　なので、　ＢＨ₁＝（ｒ₁/ｒ）（ｓ−ｂ）　となる。

このとき、

△ＡＤＣ＝（１/２）ＡＣ・ｒ₂＋（１/２）ＣＤ・ｒ₂＋（１/２）（ＢＤ−ＢＨ₁）・ｒ₂＋（１/２）（ＡＢ−ＢＨ₁）・ｒ₂

　＝（１/２）（ＡＢ＋ＢＣ＋ＣＡ）・ｒ₂−ＢＨ₁・ｒ₂＝ｓｒ₂−（ｒ₁ｒ₂/ｒ）（ｓ−ｂ）＝ｒ₂（ｓ−（ｒ₁/ｒ）（ｓ−ｂ））

以上から、　

△ＡＢＣ＝△ＡＢＤ＋△ＡＤＣ＝ｒ₁（ｓ−（ｒ₂/ｒ）（ｓ−ｃ））＋ｒ₂（ｓ−（ｒ₁/ｒ）（ｓ−ｂ））

　＝（ｒ₁＋ｒ₂）ｓ−（ｒ₁ｒ₂/ｒ）（２ｓ−ｂ−ｃ）＝（ｒ₁＋ｒ₂）ｓ−（ｒ₁ｒ₂/ｒ）ａ

　△ＡＢＣ＝ｓｒ　なので、　ｒ＝（ｒ₁＋ｒ₂）−（ｒ₁ｒ₂/ｓｒ）ａ　で、　ｓｒ＝ａｈ/２　より、

　ｒ＝（ｒ₁＋ｒ₂）−２ｒ₁ｒ₂/ｈ

となる。したがって、

　１−２ｒ/ｈ＝１−２（ｒ₁＋ｒ₂）/ｈ＋４ｒ₁ｒ₂/ｈ²＝（１−２ｒ₁/ｈ）（１−２ｒ₂/ｈ）

が成り立つ。　　（証終）


　このことを一般化して、辺ＢＣを分割して内接円の半径を、ｒ₁、ｒ₂、・・・、ｒ_ｎ とするとき、

　１−２ｒ/ｈ＝（１−２ｒ₁/ｈ）（１−２ｒ₂/ｈ）・・・（１−２ｒ_ｎ/ｈ）

が成り立つことも明らかだろう。


ここで、　ｒ/Ｒ＝（ｓ−ａ）/ｓ　、　ｓｒ＝ａｈ/２　から、

　ｒ/Ｒ＝１−ａ/ｓ＝１−ａ・（２ｒ/ａｈ）＝１−２ｒ/ｈ　すなわち、　ｒ/Ｒ＝１−２ｒ/ｈ

が成り立つので、先の結果と合わせれば、証明は合点がいくだろう。

　また、　Ｒ/ｒ＝ｓ/（ｓ−ａ）＝１＋ａ/（ｓ−ａ）＝１＋Ｒａ/（ｓｒ）＝１＋２Ｒａ/（ａｈ）＝１＋２Ｒ/ｈ

すなわち、　Ｒ/ｒ＝１＋２Ｒ/ｈ　が成り立つ。

したがって、

　１＋２Ｒ/ｈ＝（１＋２Ｒ₁/ｈ）（１＋２Ｒ₂/ｈ）・・・（１＋２Ｒ_ｎ/ｈ）

が成り立つことも明らかだろう。


　さて、△ＡＢＣの外接円の半径をＬとおくと、

　（ｒ＋Ｒ）/（２Ｌ）＝ｃｏｓＢ＋ｃｏｓＣ

が成り立つ。実際に、

　（ｒ＋Ｒ）/（２Ｌ）＝（Ｓ/ｓ＋Ｓ/（ｓ−ａ））/（２Ｌ）

　　　＝Ｓ（２ｓ−ａ）/｛ｓ（ｓ−ａ）｝×２Ｓ/（ａｂｃ）

　　　＝２（ｓ−ｂ）（ｓ−ｃ）（ｂ＋ｃ）/（ａｂｃ）

　　　＝（ｃ＋ａ−ｂ）（ａ＋ｂ−ｃ）（ｂ＋ｃ）/（２ａｂｃ）

　　　＝｛ａ²−（ｂ−ｃ）²｝（ｂ＋ｃ）/（２ａｂｃ）

　　　＝（ａ²ｂ＋ａ²ｃ−ｂ³−ｂ²ｃ＋２ｂ²ｃ＋２ｂｃ²−ｂｃ²−ｃ³）/（２ａｂｃ）

　　　＝｛ｂ（ｃ²＋ａ²−ｂ²）＋ｃ（ａ²＋ｂ²−ｃ²）｝/（２ａｂｃ）

　　　＝（ｃ²＋ａ²−ｂ²）/（２ｃａ）＋（ａ²＋ｂ²−ｃ²）｝/（２ａｂ）

　　　＝ｃｏｓＢ＋ｃｏｓＣ


　△ＡＢＣの辺ＢＣ上に点Ｄをとる。△ＡＢＤ、△ＡＤＢの内接円の半径をそれぞれ ｒ₁、ｒ₂ と
おく。

　△ＡＢＤ、△ＡＤＢの傍接円の半径をそれぞれ Ｒ₁、Ｒ₂ とおき、△ＡＢＤ、△ＡＤＢの外接円
の半径をそれぞれ Ｌ₁、Ｌ₂ とおく。

　このとき、上記の公式から、

　（ｒ₁＋Ｒ₁）/（２Ｌ₁）＝ｃｏｓＢ＋ｃｏｓ∠ＡＤＢ

　（ｒ₂＋Ｒ₂）/（２Ｌ₂）＝ｃｏｓ∠ＡＤＣ＋ｃｏｓＣ

が言える。ここで、ｃｏｓ∠ＡＤＣ＝ｃｏｓ（π−∠ＡＤＢ）＝−ｃｏｓ∠ＡＤＢ　なので、

　（ｒ₁＋Ｒ₁）/（２Ｌ₁）＋（ｒ₂＋Ｒ₂）/（２Ｌ₂）＝ｃｏｓＢ＋ｃｏｓＣ

すなわち、　（ｒ₁＋Ｒ₁）/（２Ｌ₁）＋（ｒ₂＋Ｒ₂）/（２Ｌ₂）＝（ｒ＋Ｒ）/（２Ｌ）　が成り立つ。

　同様にして、

（ｒ₁＋Ｒ₁）/（２Ｌ₁）＋（ｒ₂＋Ｒ₂）/（２Ｌ₂）＋・・・＋（ｒ_ｎ＋Ｒ_ｎ）/（２Ｌ_ｎ）＝（ｒ＋Ｒ）/（２Ｌ）

が成り立つことが分かる。


（追記）　令和４年１月２７日付け

　傍接円に関係する話題をもう一つ取り上げよう。

　∠ＰＢＱとその内部の点Ｍと数 ｓ が与えられている。点Ｍを通る直線を引き、ＰＢ、ＱＢと
交わる点をそれぞれＡ、Ｃとおくと、△ＡＢＣが作られる。

　

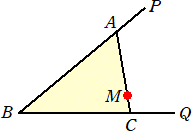
　このとき、ＡＢ＋ＢＣ＋ＣＡ＝２ｓ となるように、△ＡＢＣが作れることを示したい。

（手順）　直線ＰＢ上に、ＢＴ＝ｓ となる点Ｔをとり、ＴにおけるＰＢの垂線と∠ＰＢＱの２等分線
　　　　との交点をＯとする。Ｏを中心とし、ＯＴを半径とする円を描き、Ｍを通る接線を引けば
　　　　よい。

　

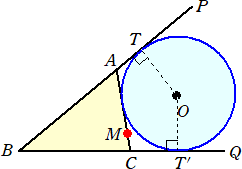
　実際に、円Ｏと直線ＡＣ、ＱＢとの接点をそれぞれＮ、Ｔ’とおくと、

　２ＢＴ＝ＢＴ＋ＢＴ’＝（ＢＡ＋ＡＮ）＋（ＢＣ＋ＣＮ）＝ＡＢ＋ＢＣ＋ＣＡ

より、　ＡＢ＋ＢＣ＋ＣＡ＝２ｓ　が成り立つ。

（→　参考：「傍接円の話題」、「周の長さ２ｐの三角形」）


（追記）　令和４年１月２９日付け

　上記では、暗黙の了解で、△ＡＢＣの∠Ａに対する傍接円の半径をＲとしてきたが、これか
らは、Ｒ_Ａと記すことにしよう。

　このとき、今までの結果から、　ｒ/Ｒ_Ａ＝（ｓ−ａ）/ｓ　である。

　ここで、△ＡＢＣ　において、ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ　とし、ｓ＝（ａ＋ｂ＋ｃ）/２　である。

　同様にして、　ｒ/Ｒ_Ｂ＝（ｓ−ｂ）/ｓ　、ｒ/Ｒ_Ｃ＝（ｓ−ｃ）/ｓ　が成り立つ。

　このとき、　１/Ｒ_Ａ＋１/Ｒ_Ｂ＋１/Ｒ_Ｃ＝１/ｒ　が成り立つ。

　実際に、

　ｒ/Ｒ_Ａ＋ｒ/Ｒ_Ｂ＋ｒ/Ｒ_Ｃ＝（ｓ−ａ）/ｓ＋（ｓ−ｂ）/ｓ＋（ｓ−ｃ）/ｓ＝（３ｓ−ａ−ｂ−ｃ）/ｓ＝１

より、　１/Ｒ_Ａ＋１/Ｒ_Ｂ＋１/Ｒ_Ｃ＝１/ｒ　が成り立つ。

　また、　ｒ/Ｒ_Ａ＝（ｓ−ａ）/ｓ　より、　Ｒ_Ａ＝Ｓ/（ｓ−ａ）　が成り立つ。

同様にして、　Ｒ_Ｂ＝Ｓ/（ｓ−ｂ）　、Ｒ_Ｃ＝Ｓ/（ｓ−ｃ）　が成り立つ

このとき、　ｒＲ_ＡＲ_ＢＲ_Ｃ＝Ｓ²　が成り立つ。

　実際に、Ｒ_ＡＲ_ＢＲ_Ｃ＝Ｓ³/（ｓ−ａ）（ｓ−ｂ）（ｓ−ｃ）＝Ｓ³/（Ｓ²/ｓ）＝ｓ・Ｓ＝（１/ｒ）Ｓ²　より、

　ｒＲ_ＡＲ_ＢＲ_Ｃ＝Ｓ²　が成り立つ。

よって、　１/Ｒ_Ａ＋１/Ｒ_Ｂ＋１/Ｒ_Ｃ＝１/ｒ　の両辺に、ｒ²Ｒ_ＡＲ_ＢＲ_Ｃ を掛ければ、

　ｒ²（Ｒ_ＡＲ_Ｂ＋Ｒ_ＢＲ_Ｃ＋Ｒ_ＣＲ_Ａ）＝ｒＲ_ＡＲ_ＢＲ_Ｃ　である。

すなわち、　ｒ²（Ｒ_ＡＲ_Ｂ＋Ｒ_ＢＲ_Ｃ＋Ｒ_ＣＲ_Ａ）＝Ｓ²　が成り立つ。


（追記）　令和４年１月３０日付け

　今までは、内接円や傍接円、外接円の半径について興味ある性質を調べてきたが、今度
は角の大きさについて調べていこうと思う。

　

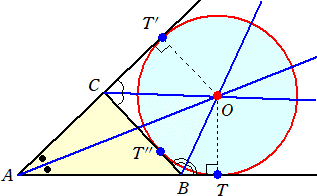
　上図において、　∠ＣＡＢ＋（１８０°−∠Ｔ’ＣＢ）＋（１８０°−∠ＴＢＣ）＝１８０°なので、

　　∠ＣＡＢ＝∠Ｔ’ＣＢ＋∠ＴＢＣ−１８０°

が成り立つ。

　また、　∠ＢＯＣ＝１８０°−（∠Ｔ’ＣＢ＋∠ＴＢＣ）/２＝９０°−（１/２）∠ＣＡＢ　より、

　　∠ＢＯＣ＝９０°−（１/２）∠ＣＡＢ

が成り立つ。

　また、　∠ＡＢＣ＝∠Ｔ’ＣＢ−∠ＣＡＢ　である。

　ところで、　∠ＡＯＣ＝（１/２）∠Ｔ’ＣＢ−（１/２）∠ＣＡＢ　なので、

　　∠ＡＢＣ＝２∠ＡＯＣ

が成り立つ。


　ここで、次の問題を考えてみよう。

問題　上図において、∠ＡＣＢ＝５８°のとき、∠ＡＯＢの大きさを求めよ。

（解）　∠ＡＣＢ＝∠ＴＢＣ−∠ＣＡＢ　で、　∠ＡＯＢ＝（１/２）∠ＴＢＣ−（１/２）∠ＣＡＢ

　　　より、　∠ＡＣＢ＝２∠ＡＯＢ　が成り立つので、　∠ＡＯＢ＝５８°÷２＝２９°　　（終）


（コメント）　△ＡＢＣの∠Ａに対する傍接円の中心をＯとすると、

　∠ＢＯＣ＝（∠Ｂ＋∠Ｃ）/２

という性質は面白いですね！

　∠ＢＯＣ＝９０°−（１/２）∠ＣＡＢ　より、

　２∠ＢＯＣ＝１８０°−∠ＣＡＢ＝∠ＡＢＣ＋∠ＡＣＢ

からも、明らかですね。


（追記）　令和４年２月１３日付け

　△ＡＢＣにおいて、重心はＧ、内心はＩ、外心はＯ、垂心はＨが慣例で用いられる。これらは
一つの三角形に対して、一つしか存在しない。それに対して、傍接円の中心（傍心）は、一つ
の三角形に対して、三つ存在するという、三角形の五心の中では異端児である。そういう訳
で、傍心を表す記号として、所謂余り物の「Ｊ」が用いられる場合が多い。

　傍心に関する次の問題を考えてみよう。

問題　　△ＡＢＣにおいて、∠Ａ、∠Ｂ、∠Ｃに対する傍心を、それぞれＪ_Ａ、Ｊ_Ｂ、Ｊ_Ｃとおく。

　　

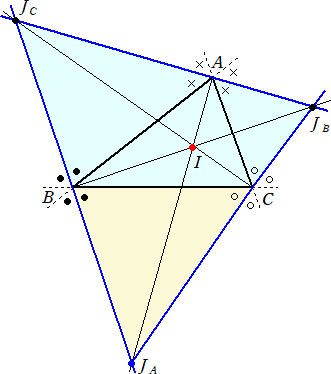
　このとき、　△Ｊ_ＡＢＣ∽△Ｊ_ＡＪ_ＢＪ_Ｃ であることを証明せよ。


（解）　△Ｊ_ＡＢＣと△Ｊ_ＡＪ_ＢＪ_Ｃにおいて、まず、∠ＢＪ_ＡＣは共通

　また、三角形の外角の和は３６０°なので、

　２●＋２○＋２×＝３６０°より、　●＋○＋×＝１８０°　即ち、　●＝１８０°−○−×

　これは、　∠Ｊ_ＡＢＣ＝∠Ｊ_ＡＪ_ＢＪ_Ｃ　が成り立つことを示す。

　よって、２角相等により、　△Ｊ_ＡＢＣ∽△Ｊ_ＡＪ_ＢＪ_Ｃ である。　　（終）


（コメント）　△ＡＢＣとその傍心Ｊ_Ａ、Ｊ_Ｂ、Ｊ_Ｃ について、∠Ｊ_ＡＢＣ＝∠Ｊ_ＡＪ_ＢＪ_Ｃ　という美
　　　　　　しい関係があることに感動しました！


（追記）　令和４年２月２日付け

　角の大きさに関する問題が余りないので、長さの計算に戻って、次の問題を考えてみよう。

問題　∠Ａ＝６０°である△ＡＢＣの底辺ＢＣ上に半円Ｏが内接しており、その接点をＰ、Ｑと
　　おく。∠Ａの２等分線は中心Ｏを通るものとする。弧ＰＱ上に点Ｒをとり、点Ｒで半円Ｏに接
　　する接線を引き、ＡＢ、ＡＣとの交点をそれぞれＤ、Ｅとおく。

　　ＡＤ＝８、ＡＥ＝３のとき、半円０の半径を求めよ。

（解）　題意に従い作図すると、
　

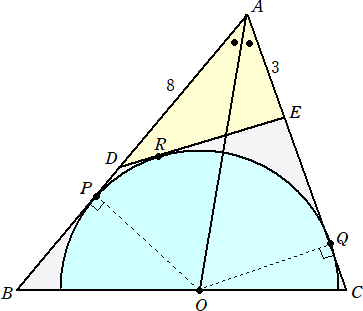
　ＤＥ²＝８²＋３²−２・８・３ｃｏｓ６０°＝７３−２４＝４９　より、　ＤＥ＝７

よって、　ｓ＝（８＋３＋７）/２＝９　より、　ＡＰ＝９

従って、半円Ｏの半径は、　９ｔａｎ３０°＝３　となる。　　（終）


（追記）　令和４年２月５日付け

　令和４年１月２９日付けで示した公式：　１/Ｒ_Ａ＋１/Ｒ_Ｂ＋１/Ｒ_Ｃ＝１/ｒ　を正三角形に
適用すれば、

　３/Ｒ＝１/ｒ　すなわち、　Ｒ＝３ｒ

の成り立つことが分かる。

例　１辺の長さ２の正三角形ＡＢＣにおいて、Ｒ＝ は自明なので、ｒ＝Ｒ/３＝１/ も
　　容易だろう。


（追記）　令和４年２月７日付け

　△ＡＢＣの傍接円において、頂点と接点を結ぶ線分の長さが三角形の周の長さの半分と
いう性質を知っていれば簡単に解ける問題が中学校入試に出題されている。

問題　下図において、傍接円の半径 ｒ を求めよ。（久留米大附設中学）

　

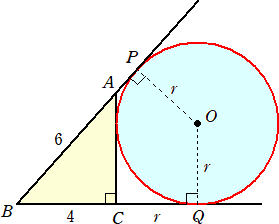
（解）　三平方の定理より、　ＡＣ＝２　なので、　２ｓ＝１０＋２　より、　ｓ＝５＋

　傍接円の性質より、　ＢＱ＝４＋ｒ＝ｓ　なので、　ｒ＝１＋　　（終）


　上記では、直角三角形という特別な場合であったが、一般の場合も同様である。

問題　下図において、傍接円の半径 ｒ を求めよ。

　

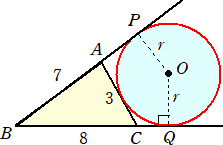
（解）　上図より、ｓ＝９　なので、傍接円の性質より、　ＣＱ＝１

　また、　∠ＡＣＢ＝６０°なので、　ｒ＝ｔａｎ６０°＝　　（終）


（追記）　令和４年３月９日付け

　上記の計算では、内接円・外接円・傍接円の半径やそれらに関する角の大きさについての
諸性質を見てきた。今度は、三角形の頂点から三角形の５心（内心・外心・傍心・垂心・重心）
までの距離を求めることを考えよう。

　次の問題が、静岡大学（２０１４）で出題されている。若干、改題しました。

問題　　ＡＢ＝７、ＢＣ＝８、ＣＡ＝５の△ＡＢＣにおいて、∠Ａに対する傍接円の中心をＪとお
　　　　くとき、ＡＪの長さを求めよ。

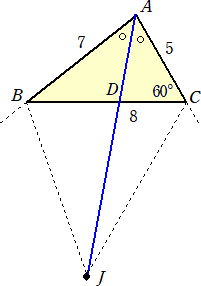余弦定理から、 　　　ｃｏｓＣ＝（８2＋５2−７2）/（２・８・５）＝１/２　より、 　　　Ｃ＝６０°なので、△ＡＢＣは特別な三角形である。 　この場合は、６０°の特性を利用すれば、次のように解く ことが出来る。

（解）　ｓ＝（８＋５＋７）/２＝１０　、△ＡＢＣ＝（１/２）８・５・ｓｉｎ６０°＝１０　より、

　　△ＡＢＣの内接円の半径 ｒ ＝１０/１０＝

　よって、△ＡＢＣの傍接円の半径 Ｒ ＝（ｓ−ｂ）（ｓ−ｃ）/ｒ ＝５・３/＝５

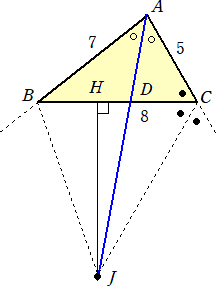よって、　ＨＪ＝Ｒ＝５　で、∠ＢＣＪ＝６０°　なので、 　　ＣＪ＝１０　となる。 　　△ＣＡＪにおいて、余弦定理を用いて、 　　　ＡＪ2＝５2＋１０2−２・５・１０ｃｏｓ１２０°＝１７５ 　　　よって、　ＡＪ＝５　　（終）

　上記の（解）では、６０°の特性に随分助けられた感が否めないが、一般的には、どう解
けばいいのだろうか？これが、次の課題である。

（別解）　点Ｊより、直線ＡＢに垂線を下ろし、その交点をＨとする。このとき、ＡＨ＝ｓ＝１０

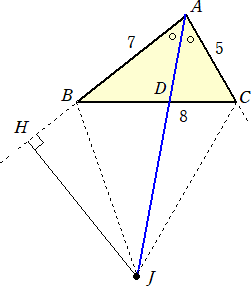よって、　ＡＨ＝（１０/７）ＡＢ 　　ＡＪ＝ｋ（（１/７）ＡＢ＋（１/５）ＡＣ）　（ｋ は定数） 　　より、　ＪＨ＝（（１０−ｋ）/７）ＡＢ−（ｋ/５）ＡＣ 　　ＪＨ⊥ＡＢ　から、　ＪＨ・ＡＢ＝０　なので、 　ＪＨ・ＡＢ＝（１０−ｋ）/７）・４９−（ｋ/５）ＡＢ・ＡＣ ここで、ＡＢ・ＡＣ＝７・５・（４９＋２５−６４）/７０＝５ なので、　ＪＨ・ＡＢ＝７０−７ｋ−ｋ＝７０−８ｋ＝０ 　よって、　ｋ＝７０/８　となる。

　このとき、　ＡＪ＝（５/４）ＡＢ＋（７/４）ＡＣ　と書けることが分かった。

　これを利用すれば、

　ＡＪ²＝（２５/１６）・４９＋（３５/８）・５＋（４９/１６）・２５＝１７５　より、　ＡＪ＝５　　（終）


　上記の計算を一般化するのは容易だろう。

　点Ｊより、直線ＡＢに垂線を下ろし、その交点をＨとする。このとき、ＡＨ＝ｓ　である。

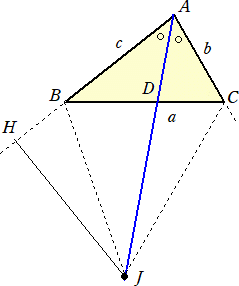よって、　ＡＨ＝（ｓ/ｃ）ＡＢ 　　ＡＪ＝ｋ（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ）　（ｋ は定数）　より、 　　ＪＨ＝（ｓ/ｃ−ｋｂ/（ｂ＋ｃ））ＡＢ−（ｋｃ/（ｂ＋ｃ））ＡＣ 　　ＪＨ⊥ＡＢ　から、　ＪＨ・ＡＢ＝０　なので、 ＪＨ・ＡＢ ＝（ｓ/ｃ−ｋｂ/（ｂ＋ｃ））ｃ2−（ｋｃ/（ｂ＋ｃ））（ｂ2＋ｃ2−ａ2）/２ なので、　ＪＨ・ＡＢ＝０　から、 　　ｋ（２ｂｃ＋ｂ2＋ｃ2−ａ2）＝２ｓ（ｂ＋ｃ）

　よって、　ｋ（ａ＋ｂ＋ｃ）（ｂ＋ｃ−ａ）＝（ａ＋ｂ＋ｃ）（ｂ＋ｃ）

すなわち、　ｋ＝（ｂ＋ｃ）/（ｂ＋ｃ−ａ）　となる。

　このとき、　ＡＪ＝（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ−ａ）　と書けることが分かった。

　この式は、△ＡＢＣの頂点Ａを始点とする∠Ａに関する傍心の位置ベクトルが求められたこ
とを意味するもので、当初の目標の一つを得ることができた。

　ただ、上記の計算は若干遠回りになっている感が否めない。次のように、内積を使わずに
も証明できる。

（証明）　内角の２等分線の性質から、　ＢＤ ： ＤＣ＝ｃ ： ｂ　なので、

　　　ＡＤ＝（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ）

　また、∠Ｂの外角の２等分線の性質から、ＡＪ ： ＪＤ＝ｃ ： ａｃ/（ｂ＋ｃ）＝ｂ＋ｃ ： ａ なので、

　　ＡＪ＝｛（ｂ＋ｃ）/（ｂ＋ｃ−ａ）｝ＡＤ＝（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ−ａ）　　（証終）


　傍心Ｊについて、次の性質が成り立つことが知られている。

　ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ の△ＡＢＣにおいて、外心をＯ、∠Ａに対する傍接円の中
心をＪとおく。また、∠Ｃの２等分線と辺ＡＢの交点をＥ、∠Ｂの２等分線と辺ＣＡの交
点をＦ とおく。

　このとき、　ＯＪ⊥ＥＦ　が成り立つ。

（証明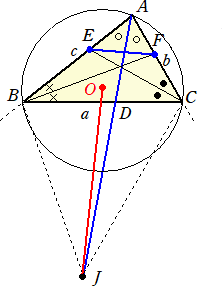）	外心Ｏを位置ベクトルの原点とし、Ａ（ａ）、Ｂ（ｂ）、Ｃ（ｃ） とする。このとき、 　ＡＥ＝（ｂ/（ａ＋ｂ））ＡＢ　、ＡＦ＝（ｃ/（ｃ＋ａ））ＡＣ なので、　ＥＦ＝（ｃ/（ｃ＋ａ））ＡＣ−（ｂ/（ａ＋ｂ））ＡＢ また、　ＡＪ＝（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ−ａ）　なので、 　ＯＪ＝ａ＋（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ−ａ） ここで、 　ＡＢ・ＡＣ＝（ｂ2＋ｃ2−ａ2）/２　なので、

ＯＪ・ＥＦ

＝｛ａ＋（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ−ａ）｝・｛（ｃ/（ｃ＋ａ））ＡＣ−（ｂ/（ａ＋ｂ））ＡＢ｝

＝（ｃ/（ｃ＋ａ））ａ・ＡＣ−（ｂ/（ａ＋ｂ））ａ・ＡＢ

　＋ｂ²ｃ²（ｂ−ｃ）/｛（ｂ＋ｃ−ａ）（ａ＋ｂ）（ｃ＋ａ）｝

　＋ｂｃ（ｂ−ｃ）（ｂ²＋ｃ²−ａ²）/｛２（ｂ＋ｃ−ａ）（ａ＋ｂ）（ａ＋ｃ）｝

＝（ｃ/（ｃ＋ａ））ａ・ＡＣ−（ｂ/（ａ＋ｂ））ａ・ＡＢ＋ｂｃ（ｂ−ｃ）（ａ＋ｂ＋ｃ）/｛２（ａ＋ｂ）（ｃ＋ａ）｝

　ここで、ＡＣ、ＡＢの中点をそれぞれＭ、Ｎとおく。

　ａ＝ＯＭ＋ＭＡ　と分解すると、ＯＭ⊥ＡＣ より、　ａ・ＡＣ＝ＭＡ・ＡＣ＝−（１/２）ｂ²

同様にして、　ａ・ＡＢ＝−（１/２）ｃ²　が成り立つ。

　したがって、

　ＯＪ・ＥＦ

＝−（１/２）ｂ²ｃ/（ｃ＋ａ）＋（１/２）ｂｃ²/（ａ＋ｂ）＋ｂｃ（ｂ−ｃ）（ａ＋ｂ＋ｃ）/｛２（ａ＋ｂ）（ｃ＋ａ）｝

＝｛−ｂ²ｃ（ａ＋ｂ）＋ｂｃ²（ｃ＋ａ）＋ｂｃ（ｂ−ｃ）（ａ＋ｂ＋ｃ）｝/｛２（ａ＋ｂ）（ｃ＋ａ）｝

＝０

　以上から、　ＯＪ⊥ＥＦ　が成り立つ。　　（証終）


（コメント）　しばらくの間、ａ・ＡＣ、ａ・ＡＢ の処理をどうしたものかと思案していましたが、当
　　　　　　ＨＰの掲示板「出会いの泉」のDD++さんからのコメント（No.１６　３/２９ 19:18）で解
　　　　　　決策をご教示いただいて、無事証明を完結することが出来ました。DD++さんに感
　　　　　　謝いたします。


（追記）　令和４年３月３０日付け

　上記の計算から、　ＡＪ＝（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ−ａ）　と書けることが分かった。この式
より、頂点Ａと傍心Ｊを結ぶ線分ＡＪの長さを計算することは容易だろう。

　実際に、

　ＡＪ²＝（ｂＡＢ＋ｃＡＣ）・（ｂＡＢ＋ｃＡＣ）/（ｂ＋ｃ−ａ）²＝ｂｃ（ａ＋ｂ＋ｃ）/（ｂ＋ｃ−ａ）

から、　ＡＪ＝√｛ｂｃ（ａ＋ｂ＋ｃ）/（ｂ＋ｃ−ａ）｝　である。


　次に、△ＡＢＣの内心 Ｉ について、頂点Ａと内心 Ｉ を結ぶ線分ＡＩ の長さを求めてみよう。

　 △ＡＢＣ において、ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ とおく。

　

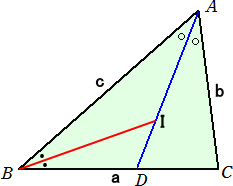
　角の二等分線の長さの公式から、 ＡＤ²＝ＡＢ・ＡＣ−ＢＤ・ＤＣ　であるので、

　ＡＤ²＝ｂｃ−（ｃａ/（ｂ＋ｃ））（ａｂ/（ｂ＋ｃ））＝ｂｃ（ａ＋ｂ＋ｃ）（ｂ＋ｃ−ａ）/（ｂ＋ｃ）²

ここで、　ＢＤ＝ｃａ/（ｂ＋ｃ）　なので、　ＡＩ ： ＩＤ＝c ： ｃａ/（ｂ＋ｃ）＝ｂ＋ｃ ： ａ

よって、

ＡＩ＝（（ｂ＋ｃ）/（ａ＋ｂ＋ｃ））√｛ｂｃ（ａ＋ｂ＋ｃ）（ｂ＋ｃ−ａ）｝/（ｂ＋ｃ）＝√｛ｂｃ（ｂ＋ｃ−ａ）/（ａ＋ｂ＋ｃ）｝

で与えられる。


（コメント）　２ｓ＝ａ＋ｂ＋ｃ　により、ｓ を定めると、

　ＡＪ＝√｛ｂｃ・ｓ/（ｓ−ａ｝

であり、　ＡＩ＝√｛ｂｃ・（ｓ−ａ）/ｓ｝　なんですね！逆数っぽい雰囲気です．．．。

　ＡＩ・ＡＪ＝ｂｃ　などという性質に魅せられます！


（追記）　令和４年４月１４日付け

　さて、当初の目標「三角形の頂点から三角形の５心（内心・外心・傍心・垂心・重心）までの
距離を求める」という問題について検討を続けよう。

　△ＡＢＣの外心をＯ、重心をＧ、垂心をＨとおく。また、Ｒは△ＡＢＣの外接円の半径である。
ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ とする。

　ＡＯ＝Ｒ＝ａｂｃ/（４Ｓ）＝ａｂｃ/（４）

＝ａｂｃ/√｛（ａ＋ｂ＋ｃ）（ｂ＋ｃ−ａ）（ａ−ｂ＋ｃ）（ａ＋ｂ−ｃ）｝


＃角の大きさも使ってよければ、もちろん、正弦定理から、　ＡＯ＝Ｒ＝ａ/ｓｉｎＡ　である。

　また、ＡＧ＝（ＡＢ＋ＡＣ）/３　なので、

　｜ＡＧ｜²＝（｜ＡＢ｜²＋２ＡＢ・ＡＣ＋｜ＡＣ｜²）/９＝（２ｂ²＋２ｃ²−ａ²）/９

よって、　ＡＧ＝√（２ｂ²＋２ｃ²−ａ²）/３

（別解）　中線定理より、　ｂ²＋ｃ²＝２（ＡＭ²＋ａ²/４）　で、　ＡＧ＝（２/３）ＡＭ　から、

　　ｂ²＋ｃ²＝２（（９/４）ＡＧ²＋ａ²/４）　が成り立つ。

　よって、　２ｂ²＋２ｃ²＝９ＡＧ²＋ａ²　より、　ＡＧ²＝（２ｂ²＋２ｃ²−ａ²）/９　が成り立つ。


　以下で、∠Ａは鋭角とする。

　よく知られているように、　ＯＨ＝ＯＡ＋ＯＢ＋ＯＣ　と表せる。

実際に、ＡＨ・ＢＣ＝（ＯＢ＋ＯＣ）・（ＯＣ−ＯＢ）＝｜ＯＣ｜²−｜ＯＢ｜²＝Ｒ²−Ｒ²＝０

　から、　ＡＨ⊥ＢＣ　である。同様にして、　ＢＨ⊥ＣＡ　、ＣＨ⊥ＡＢ　から、Ｈは垂心である。

　このとき、

　｜ＡＨ｜²＝（｜ＯＢ｜²＋２ＯＢ・ＯＣ＋｜ＯＣ｜²）＝４Ｒ²−ａ²

　ここで、　Ｒ＝ａ/（２ｓｉｎＡ）　なので、　４Ｒ²＝ａ²/（１−ｃｏｓ²Ａ）

　よって、　｜ＡＨ｜²＝ａ²ｃｏｓ²Ａ/（１−ｃｏｓ²Ａ）

　余弦定理より、　ｃｏｓＡ＝（ｂ²＋ｃ²−ａ²）/（２ｂｃ）　なので、上式に代入して、

　｜ＡＨ｜²＝ａ²（ｂ²＋ｃ²−ａ²）²/｛（ａ＋ｂ＋ｃ）（ｂ＋ｃ−ａ）（ａ−ｂ＋ｃ）（ａ＋ｂ−ｃ）｝

よって、　ＡＨ＝ａ（ｂ²＋ｃ²−ａ²）/√｛（ａ＋ｂ＋ｃ）（ｂ＋ｃ−ａ）（ａ−ｂ＋ｃ）（ａ＋ｂ−ｃ）｝


　ＡＨの計算について、次のような別解が考えられる。

（別解）　直線ＡＨと辺ＢＣとの交点をＥ、直線ＢＨと辺ＣＡとの交点をＦとおく。

　このとき、　ＡＨ＝ＡＦ/ｃｏｓ∠ＣＡＥ＝ＡＢｃｏｓＡ/ｓｉｎ∠ＡＣＥ＝２ＲｃｏｓＡ　である。

よって、

ＡＨ＝ａ（ｂ²＋ｃ²−ａ²）/（４Ｓ）

　＝ａ（ｂ²＋ｃ²−ａ²）/√｛（ａ＋ｂ＋ｃ）（ｂ＋ｃ−ａ）（ａ−ｂ＋ｃ）（ａ＋ｂ−ｃ）｝


（追記）　令和４年４月１５日付け

　△ＡＢＣの内接円の半径を ｒ 、外接円の半径を Ｒ とおくとき、次の等式が成り立つ。

　ｒ ＝４Ｒｓｉｎ（Ａ/２）ｓｉｎ（Ｂ/２）ｓｉｎ（Ｃ/２）


　実際に、Ｓ＝ａｂｃ/（４Ｒ）＝ｒ（ａ＋ｂ＋ｃ）/２　より、　２Ｒｒ（ａ＋ｂ＋ｃ）＝ａｂｃ

　正弦定理より、　ａ＝２ＲｓｉｎＡ　、ｂ＝２ＲｓｉｎＢ　、ｃ＝２ＲｓｉｎＣ　なので、

　　４Ｒ²ｒ（ｓｉｎＡ＋ｓｉｎＢ＋ｓｉｎＣ）＝８Ｒ³ｓｉｎＡｓｉｎＢｓｉｎＣ

すなわち、　ｒ（ｓｉｎＡ＋ｓｉｎＢ＋ｓｉｎＣ）＝２ＲｓｉｎＡｓｉｎＢｓｉｎＣ

　ここで、倍角の公式と和積の公式を用いて、

　ｒ（２ｓｉｎ（（Ａ＋Ｂ）/２）ｃｏｓ（（Ａ−Ｂ）/２）＋２ｓｉｎ（（Ａ＋Ｂ）/２）ｃｏｓ（（Ａ＋Ｂ）/２））

＝１６Ｒｓｉｎ（Ａ/２）ｓｉｎ（Ｂ/２）ｓｉｎ（Ｃ/２）ｃｏｓ（Ａ/２）ｃｏｓ（Ｂ/２）ｃｏｓ（Ｃ/２）

すなわち、

　４ｒｓｉｎ（（Ａ＋Ｂ）/２）ｃｏｓ（Ａ/２）ｃｏｓ（Ｂ/２）

＝１６Ｒｓｉｎ（Ａ/２）ｓｉｎ（Ｂ/２）ｓｉｎ（Ｃ/２）ｃｏｓ（Ａ/２）ｃｏｓ（Ｂ/２）ｃｏｓ（Ｃ/２）

より、

　４ｒｃｏｓ（Ａ/２）ｃｏｓ（Ｂ/２）ｃｏｓ（Ｃ/２）

＝１６Ｒｓｉｎ（Ａ/２）ｓｉｎ（Ｂ/２）ｓｉｎ（Ｃ/２）ｃｏｓ（Ａ/２）ｃｏｓ（Ｂ/２）ｃｏｓ（Ｃ/２）

なので、

　ｒ ＝４Ｒｓｉｎ（Ａ/２）ｓｉｎ（Ｂ/２）ｓｉｎ（Ｃ/２）

が成り立つ。


　この公式については、次のような別証も考えられる。

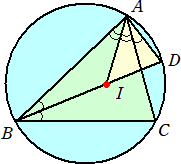左図において、　ｒ＝ＡＩ・ｓｉｎ（Ａ/２） 　また、△ＡＢＤにおいて、正弦定理より、ＡＤ/ｓｉｎ（Ｂ/２）＝２Ｒ 　このとき、 　　ｒ/Ｒ＝ＡＩ・ｓｉｎ（Ａ/２）/｛ＡＤ/（２ｓｉｎ（Ｂ/２））｝ 　　　　＝２（ＡＩ/ＡＤ）ｓｉｎ（Ａ/２）ｓｉｎ（Ｂ/２）

　ここで、　∠ＡＩＤ＝Ａ/２＋Ｂ/２＝∠ＤＡＩ　なので、△ＤＡＩは、ＤＡ＝ＤＩ の二等辺三角形

　よって、　ＡＩ＝２ＡＤｃｏｓ（（Ａ＋Ｂ）/２）＝２ＡＤｃｏｓ（π/２−Ｃ/２）＝２ＡＤｓｉｎ（Ｃ/２）　より、

　　ＡＩ/ＡＤ＝２ｓｉｎ（Ｃ/２）　なので、　ｒ/Ｒ＝４ｓｉｎ（Ａ/２）ｓｉｎ（Ｂ/２）ｓｉｎ（Ｃ/２）

　したがって、　ｒ ＝４Ｒｓｉｎ（Ａ/２）ｓｉｎ（Ｂ/２）ｓｉｎ（Ｃ/２）　が示された。


（追記）　令和５年１月３１日付け

　上記と同様の問題が、東北大学前期理系（２０１８）で出題されている。

第４問　△ＡＢＣの内接円の半径を ｒ、外接円の半径をＲとし、ｈ＝ｒ/Ｒ とする。また、
　　　　∠A＝２α、∠Ｂ＝２β、∠Ｃ＝２γ とおく。

（１）　ｈ＝４ｓｉｎαｓｉｎβｓｉｎγ　となることを示せ。

（２）　直角三角形ＡＢＣにおいて、ｈ≦−１ であることを示せ。また、等号成立を調べよ。

（３）　一般の△ＡＢＣにおいて、ｈ≦１/２　であることを示せ。また、等号成立を調べよ。


（解）（１）　ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ　とし、内心を Ｉ とおく。内接円と辺ＢＣとの接点をＤとお

　くと、　ｒ＝ＢＤ・ｔａｎβ＝ＣＤ・ｔａｎγ　から、　ａ＝ｒ/ｔａｎβ＋ｒ/ｔａｎγ　なので、

　　ｒ＝ａ・ｔａｎβｔａｎγ/（ｔａｎβ＋ｔａｎγ）

　正弦定理より、　ａ＝２Ｒｓｉｎ２α　なので、　ｒ＝４Ｒｓｉｎαｃｏｓα・ｔａｎβｔａｎγ/（ｔａｎβｔａｎγ）

　よって、　ｈ＝４ｓｉｎαｃｏｓα・ｔａｎβｔａｎγ/（ｔａｎβ＋ｔａｎγ）

ここで、　β＋γ＝π/２−α　なので

　ｔａｎβｔａｎγ/（ｔａｎβ＋ｔａｎγ）

＝ｓｉｎβｓｉｎγ/（ｓｉｎβｃｏｓγ＋ｃｏｓβｓｉｎγ）

＝ｓｉｎβｓｉｎγ/ｓｉｎ（β＋γ）

＝ｓｉｎβｓｉｎγ/ｃｏｓα

　よって、　ｈ＝４ｓｉｎαｃｏｓα・ｓｉｎβｓｉｎγ/ｃｏｓα＝４ｓｉｎαｓｉｎβｓｉｎγ　が成り立つ。

（２）　題意より、∠Ｃ＝２γ＝π/２　としても一般性は失われない。

　このとき、　α＋β＝π/４　であることに注意して、

ｈ＝４ｓｉｎαｓｉｎβｓｉｎγ

　＝２ｓｉｎαｓｉｎβ

　＝（ｃｏｓ（α−β）−ｃｏｓ（α＋β））

　＝（ｃｏｓ（α−β）−１/）

ここで、０＜α、β＜π/４　より、　−π/４＜α−β＜π/４　なので、

　１/＜ｃｏｓ（α−β）≦１　となり、　ｈ≦（１−１/）＝−１　である。

　等号成立は、　ｃｏｓ（α−β）＝１　すなわち、　α−β＝０　のときで、

　α＋β＝π/４　より、　α＝β＝π/８　なので、　２α＝２β＝π/４

　以上から、直角２等辺三角形のとき、等号成立である。

（３）　α＋β＋γ＝π/２　に注意して、積和の公式より、

ｈ＝４ｓｉｎαｓｉｎβｓｉｎγ

　＝２（ｃｏｓ（α−β）−ｃｏｓ（α＋β））ｓｉｎγ

　＝２（ｃｏｓ（α−β）−ｃｏｓ（π/２−γ））ｓｉｎγ

　＝２（ｃｏｓ（α−β）−ｓｉｎγ）ｓｉｎγ

　＝−２ｓｉｎ²γ＋２ｃｏｓ（α−β）ｓｉｎγ

　＝−２｛ｓｉｎγ−（１/２）ｃｏｓ（α−β）｝²＋（１/２）ｃｏｓ²（α−β）

　ここで、　−π/２＜α−β＜π/２　より、　０＜ｃｏｓ（α−β）≦１　すなわち、

　０＜ｃｏｓ²（α−β）≦１　なので、　ｈ≦１/２　であることが分かる。

　等号成立は、　ｓｉｎγ＝（１/２）ｃｏｓ（α−β）　かつ　ｃｏｓ（α−β）＝１　のとき。

　よって、　ｓｉｎγ＝１/２　より、　γ＝π/６　で、　α−β＝０　から、　α＝β＝π/６

　以上から、正三角形のとき、等号成立である。　　（終）



　　以下、工事中！