2重根号 
現行の学習指導要領では指導外の内容に追いやられていた「2重根号」が、平成24年
からの新学習指導要領で復活することになった。指導外の内容とはいえ、今でも教科書等
には「発展的内容」として扱われており、進学校では当然のごとく教えられていることと思う。
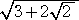 は、やはり、簡単に
は、やはり、簡単に  +1 と表したいものだ。新学習指導要領は窮屈
+1 と表したいものだ。新学習指導要領は窮屈
だった「計算の制限」を撤廃した点で評価される。ただ、新学習指導要領は、古き良き時代
を懐かしむような何となく懐古主義を彷彿させる。行列が外れ複素数平面がまた復活する!
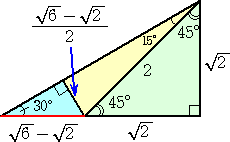
数学の問題を解いていて、2重根号を外す必要性が時々生じる。私の経験では、高校1
年のとき、sin15°の値を三角関数の加法定理によらず、図形的に求めるときに使ったこ
とが印象深い。
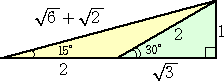 |
左図の斜辺の長さの計算で2重根号を外すことを行う。
即ち、
斜辺=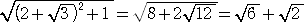
より、
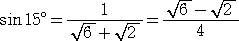 |
もっとも、この場合は、2重根号を避けて求める方法も知られている。
 |
左図とにらめっこをすると自ずから、
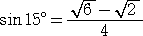
が導かれることだろう。 |
2重根号の計算を回避する第3の方法(→ 「15°の正接」)
2重根号の計算を回避する第4の方法(よおすけ氏 平成28年5月3日付け)
△ABCにおいて、BC=1+ 、CA=
、CA= 、∠C=45°を使います。
、∠C=45°を使います。
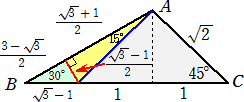 |
左図より、
tan15°={( -1)/2}/{( -1)/2}/{( +1)/2}=2- +1)/2}=2- |
このように2重根号を外す計算は、数のおおよその値を知るためにも大切な技法であり、
現学習指導要領で指導の範囲外とされたことが非常に不可解である。
2重根号を外す公式
a>b>0 のとき、
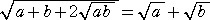

上記の公式から分かるように、2重根号が外れるためにはある種の制約条件が存在する
ので、すべての2重根号が外れるわけではない。
2重根号を外すための基本変形パターンを確認しておこう。
例1 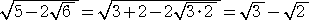
例2 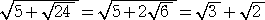
例3
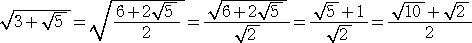
同様の問題で3乗根の場合を、当HPがいつもお世話になっているS(H)さんが提示され
た。(平成21年2月8日付け)眼前にある小高い丘を少しずつ登ってみることにしよう。
問 題 2重根号 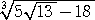 を外せ。
を外せ。
(解) 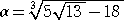 、
、  とおくと、 β<α で、
とおくと、 β<α で、
α3+β3=−36 、αβ=−1
である。このとき、 α3+β3=(α+β)3−3αβ(α+β)=−36 より、
(α+β)3+3(α+β)+36=0
x=α+β とおくと、 x3+3x+36=0 で、 (x+3)(x2−3x+12)=0
x は実数なので、 x2−3x+12≠0 より、 x=−3
このとき、 α 、β は、2次方程式 t2+3t−1=0 の解となる。
解の公式より、
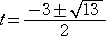
よって、 β<α より、
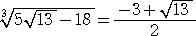 (終)
(終)
(コメント) 3乗根の場合も、ごく特殊な場合しか2重根号は外れないと予想される。2乗根
のような簡便な公式を模索したが、果たして3乗根の場合も存在するのだろうか?
今後の研究課題としよう。上記の場合は、2次方程式の問題に翻訳されてたまたま
求めることができたが、一般の場合に同様に求めることはほとんど不可能だろうと
推察される。
問 題 2重根号 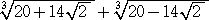 を外せ。
を外せ。
(解) 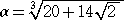 、
、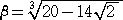 とおくと、 β<α で、
とおくと、 β<α で、
α3+β3=40 、 αβ=2
である。このとき、 α3+β3=(α+β)3−3αβ(α+β)=40 より、
(α+β)3−6(α+β)−40=0
x=α+β とおくと、 x3−6x−40=0 で、 (x−4)(x2+4x+10)=0
x は実数なので、 x2+4x+10≠0 より、 x=4
よって、 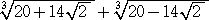 =4 (終)
=4 (終)
問 題 次の2重根号を外せ。
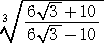
(解) 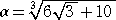 、
、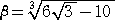 とおくと、 β<α で、
とおくと、 β<α で、
α3−β3=20 、 αβ=2 である。このとき、
α3−β3=(α−β)3+3αβ(α−β)=20 より、
(α−β)3+6(α−β)−20=0
x=α−β とおくと、 x3+6x−20=0 で、 (x−2)(x2+2x+10)=0
x は実数なので、 x2+2x+10≠0 より、 x=2 すなわち、 α−β=2
このとき、 α 、−β は、2次方程式 t2−2t−2=0 の解となる。
解の公式より、 t=1±
よって、 β<α より、 α=1+ 、 −β=1−
、 −β=1− なので、
なので、
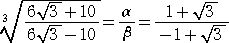 (終)
(終)
問 題 次の2重根号を外せ。
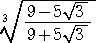
(解)
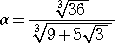
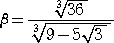
とおくと、 β>α で、 α3+β3=108 、 αβ=6 である。このとき、
α3+β3=(α+β)3−3αβ(α+β)=108 より、
(α+β)3−18(α+β)−108=0
x=α+β とおくと、 x3−18x−108=0 で、 (x−6)(x2+6x+18)=0
x は実数なので、 x2+6x+18≠0 より、 x=6 すなわち、 α+β=6
このとき、 α 、β は、2次方程式 t2−6t+6=0 の解となる。
解の公式より、 t=3±
よって、 β>α より、 α=3− 、 β=3+
、 β=3+ なので、
なので、
 (終)
(終)
(コメント) 最初は前問のように、普通に分子、分母をそれぞれ α 、 β
とおいて計算した
ところ、計算に行き詰まってしまった。そこで、逆数を考え、積 αβ が整数になるよ
うに、α 、β の分子を工夫したところ、上手く計算が進んだ。 ヨカッタ〜!
上記の問題をもっと自然に解くために、ある特殊な場合に限定されるが、3乗根の場合の
2重根号を外す公式を作ってみた。
この公式は、平成21年2月11日付けの、当HPがいつもお世話になっているS(H)さんの
コメントに触発されて作ったものである。S(H)さんに感謝します。
公 式 実数 a 、k と正数 b、m に対して、
a2−k2b=m のとき、 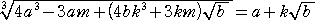
a2−k2b=−m のとき、 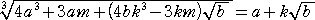
上記で計算した2重根号に公式を適用してみよう。
例 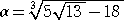 の場合
の場合
b=13 として、 52k3+3km=5 の解が簡単に見つからないので、m=1 で、
52k3−3k=5 としてみる。この方程式は、k=1/2 を解に持つ。
4a3+3a=−18 より、 a<0 で、 4a3+3a+18=0
この3次方程式は、 a=−3/2 を解に持つ。
このとき、 a2−k2b=9/4−13/4=−1 が成り立つので、
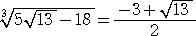
例 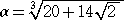 の場合
の場合
b=2 として、 8k3+3km=14 ここで、m=2 としてみると、
8k3+6k−14=0 は、明らかに k=1 を解に持つ。
4a3−6a=20 より、 4a3−6a−20=0 で、この3次方程式は、 a=2 を解に持つ。
このとき、 a2−k2b=4−2=2 が成り立つので、
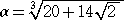 =2+
=2+
例 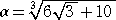 の場合
の場合
b=3 として、 12k3+3km=6 の解が簡単に見つからないので、
12k3−3km=6 において、m=2 としてみると、 12k3−6k−6=0
この3次方程式は、明らかに k=1 を解に持つ。
4a3+6a=10 より、 4a3+6a+10=0 で、明らかに解は、 a=−1
このとき、 a2−k2b=1−3=−2 が成り立つので、
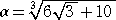 =−1+
=−1+
ここで、話を元に戻して、前述で、策を労した次の2重根号
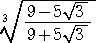
に対して、いよいよ公式を適用してみることにしよう。
そのために、根号内の分母を有理化すると 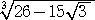 となるので、
となるので、
b=3 として、 12k3+3km=−15 において、 m=1 とすると、
3次方程式 12k3+3k+15=0 において、明らかに k=−1 を解に持つ。
4a3−3a=26 より、 4a3−3a−26=0 で、明らかに解は、 a=2
このとき、 a2−k2b=4−3=1 が成り立つので、
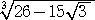 =2−
=2−
(コメント) このように考えると、この問題も他の問題と全く違和感がないですね!
問 題 次の2重根号を外せ。
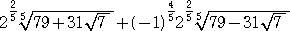
(解)
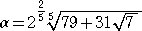 、
、 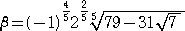
とおくと、 β<α で、 α5+β5=632 、 αβ=−6 である。このとき、
α5+β5=(α3+β3)(α2+β2)−α2β2(α+β)
={(α+β)3−3αβ(α+β)}{(α+β)2−2αβ}−α2β2(α+β)
={(α+β)3+18(α+β)}{(α+β)2+12}−36(α+β)=632
x=α+β とおくと、 (x3+18x)(x2+12}−36x−632=0 より、
x5+30x3+180x−632=0
F(x)=x5+30x3+180x−632 とおくと、
F(2)=25+30・23+180・2−632=32+240+360−632=0
よって、因数定理により、F(x)は、x−2 で割り切れる。
ところで、 F’(x)=5x4+90x2+180>0 より、 F(x)は、単調に増加するので、
方程式 F(x)=x5+30x3+180x−632=0 の解は、 x=2 のみである。
したがって、 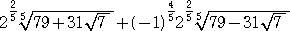 =2 となる。 (終)
=2 となる。 (終)
(コメント) 超〜複雑っぽい数が、たった「2」とは不思議ですね!
(→ 参考 :「見かけは悪いが美しい数」)
α+β=2 、 αβ=−6 なので、 α 、β は、2次方程式 t2−2t−6=0 の解となる。
解の公式より、 t=1±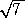
よって、 β<α より、 α=1+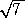 、 β=1−
、 β=1−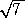 である。
である。
問 題 次の2重根号を外せ。
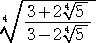
答えは、
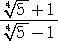
二重根号を外す問題は、ガロアの理論と密接に関係している。以下では、このことについ
て整理したいと思う。
2006年度後期に、上智大学理工学部数学科3年生を対象に行われた角皆先生の講義
録や演習、課題レポートが大いに参考になった。ここに感謝の意を表したい。
まず、次の問題を考えることにする。
問 題 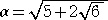 について、
について、
(1) 2重根号を外せ。
(2) α の有理数体Q上の最小多項式を求めよ。また、拡大次数 [Q(α):Q]
を求めよ。
(3) その方程式を、Ferrari の方法で解いてみよ。
(4) Q(α)=Q(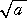 ,
,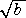 ) となる a 、b ∈Z があれば求めよ。
) となる a 、b ∈Z があれば求めよ。
(解) (1)は易しいだろう。 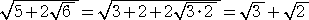 となる。
となる。
(2) (α2−5)2=24 から、 α4−10α2+1=0
したがって、代数的数 α の最小多項式は、 x4−10x2+1 となる。
(厳密には、x4−10x2+1 がQ上既約であることを示さなければならないが、
x4−10x2+1=(x2−5+2 )(x2−5−2
)(x2−5−2 )
)
=(x+ +
+ )(x+
)(x+ −
− )(x−
)(x− +
+ )(x−
)(x− −
− )
)
から明らかだろう。)
よって、拡大次数 [Q(α):Q]=4 となる。
(2重根号が外れるとき、方程式自体が特殊な形になるような...予感!)
(3) Ferrari の方法により、 x4−10x2+1=0 を解くために適当なλを用いて、
x4=10x2−1
x4+2λx2+λ2=10x2−1+2λx2+λ2
(x2+λ)2=(2λ+10)x2+λ2−1
と式変形するとき、右辺が完全平方式になればよい。
すなわち、判別式を D とすると、
D=02−4(2λ+10)(λ2−1)=−8(λ+5)(λ+1)(λ−1)=0
(このようなλに関する方程式を「分解方程式」というらしい。)
よって、 λ=−5 、−1 、1
λ=−5 のとき、 (x2−5)2=24 において、x2−5=±2 より、 x2=5±2
より、 x2=5±2
ここで、 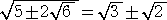 なので、x=±(
なので、x=±( ±
± ) (複号任意) となる。
) (複号任意) となる。
λ=−1 のとき、 (x2−1)2=8x2 において、x2−1=±2 x より、x2±2
x より、x2±2 x−1=0
x−1=0
よって、 x=± ±
± (複号任意) となる。 (←2重根号が外れている!)
(複号任意) となる。 (←2重根号が外れている!)
λ=1 のとき、 (x2+1)2=12x2 において、x2+1=±2 x より、x2±2
x より、x2±2 x+1=0
x+1=0
よって、 x=± ±
± (複号任意) となる。 (←2重根号が外れている!)
(複号任意) となる。 (←2重根号が外れている!)
(4) (1)より、 Q(α)=Q( ,
, ) なので、 a=2、b=3 と言える。 (終)
) なので、 a=2、b=3 と言える。 (終)
(コメント) 上記の計算(3)より、(1)のような2重根号を外す公式を知らなくても、

であることが分かるようだ。方程式を解く過程で、自然に2重根号が外れるのには感動しまし
た!
それでは、 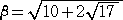 については、どのような計算結果が待ち受けているのだ
については、どのような計算結果が待ち受けているのだ
ろうか? 上記の α と同様の問題を考えてみよう。
まず、 a+b=10 、ab=17 となる a 、 b (a>b)は、2次方程式 t2−10t+17=0
の解なので、 t=5±2 である。
である。
したがって、無理をして強引に2重根号を外そうと頑張ってみるのだが、
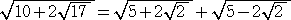
となるだけで、永遠に2重根号は外れそうにない雰囲気!この原因はどこにあるのだろう?
すぐ気がつくことは、2次方程式 t2−10t+17=0 が、整数解を持たないからだ!整数
解さえ持ってくれば、2重根号は必ず外れるのに...。
ところで、(β2−10)2=68 から、 β4−20β2+32=0
したがって、代数的数 β の最小多項式は、 x4−20x2+32 となる。
Ferrari の方法により、 x4−20x2+32=0 を解くために適当なλを用いて、
x4=20x2−32
x4+2λx2+λ2=20x2−32+2λx2+λ2
(x2+λ)2=(2λ+20)x2+λ2−32
と式変形するとき、右辺が完全平方式になればよい。すなわち、判別式を D とすると、
D=02−4(2λ+20)(λ2−32)=−8(λ+10)(λ+4 )(λ−4
)(λ−4 )=0
)=0
よって、 λ=−10 、−4 、4
、4
λ=−10 のとき、 (x2−10)2=68 において、x2−10=±2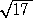 より、
より、
x2=10±2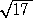
ここで、 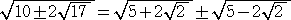 なので、
なので、
x=±(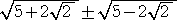 ) (複号任意) となる。
) (複号任意) となる。
λ=−4 のとき、 (x2−4
のとき、 (x2−4 )2=(20−8
)2=(20−8 )x2
)x2
λ=4 のとき、 (x2−4
のとき、 (x2−4 )2=(20−8
)2=(20−8 )x2
)x2
これらも全く2重根号が外れる気配は皆無だ!(計算打ち切り)
(追記) 平成22年2月8日付け
「2重根号が外せるか否かの一般化」と題して、当HPの掲示板「出会いの泉」に、2月4日
付けでHN「H.I.」さんより書き込みがあった。
2重根号が外せるかどうかの判定の一般化について考えたことがあり、少し式をいじって
みたところ、以下のような公式めいたものを得ることが出来ました。
A、B、Cを正の有理数(A>C>0 かつ B>0 で √Bは無理数)とする。
A2−4B=C2 を満たすCが存在するとき、2重根号 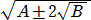 は外せて、
は外せて、
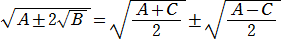
になる。
例 A=5、B=6 のとき、 A2−4B=25−24=1=12 より、 C=1 なので、
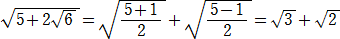
になる。
ただ、上記の公式で気になることが2つあります。
(1)判別式「A2−4B=C2 」の形で、不定方程式的な何かの匂いは感じるのですが、各変
数が有理数なのでこれをどうにかすると、もっとより一般的な議論が出来るのか、あるいは
そうではないのか。
(2)上記判別式で、Cの値が虚数になった場合、この式がどういった意味合いを持ってくるの
か。
以上の疑問点について、何かご教示くだされば幸いです。
2重根号を外す公式 a>b>0 のとき、
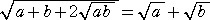

より、2重根号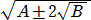 が外れるためには、A=a+b、B=ab となる正の有理数 a 、
が外れるためには、A=a+b、B=ab となる正の有理数 a 、
b が見つかればよい。H.I.さんは、 a 、b を見つけるために、2次方程式 x2−Ax+B=0
を考えられ、判別式 D=A2−4Bが完全平方(=C2)になる場合に2重根号が外せることを
示しているが、この理論はここまでで、それ以上の進展は期待できないような、そんな...
予感。 ・・・・・ (1)の回答(カナ?)
また、D<0 のときは、正の有理数 a 、b は存在し得ないので、2重根号は外せない。
・・・・・ これは、(2)の回答になっていないことが判明しました!(平成28年9月24日付け)
(追記) 当HP読者のHN「Ren」さんから二重根号を外す問題をいただきました。
(平成28年9月24日付け)
次の2重根号 √(4+3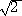 ) を外してください。(ちなみにちゃんと外れます。)
) を外してください。(ちなみにちゃんと外れます。)
DD++さんからのコメントです。(平成28年9月24日付け)
√(4+3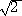 )=4√8+4
)=4√8+4 (※ 4√:4乗根) ということでしょうか?
(※ 4√:4乗根) ということでしょうか?
よおすけさんからのコメントです。(平成28年9月25日付け)
このままでは困難なので、 √(3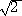 +4)=α、√(3
+4)=α、√(3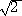 −4)=β とする。(ただし、α>β)
−4)=β とする。(ただし、α>β)
これから、 α2+β2=6 、αβ=
、αβ= が得られ、α2+β2=(α+β)2-2αβ=6
が得られ、α2+β2=(α+β)2-2αβ=6
より、 (α+β)2=8 が成り立つ。このとき、α>0、β>0 で、α+β>0 より、
が成り立つ。このとき、α>0、β>0 で、α+β>0 より、
α+β=√(8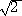 )=√√128=4√16×4√8=2・4√8
)=√√128=4√16×4√8=2・4√8
よって、αとβは、x の2次方程式 x2−2x・4√8+ =0 の2つの解。これを解いて、
=0 の2つの解。これを解いて、
x=4√8+4 、4√8−4
、4√8−4
ここで、α>βより、 α=√(3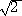 +4)=4√8+4
+4)=4√8+4
(コメント) H.I.さんからの質問で、Renさんの問題は、D=−2<0 の場合にも2重根号
が外せる例があることを示しています。Renさんに感謝します。
Renさんからのコメントです。(平成28年9月25日付け)
DD++さん、よおすけさん、解答ありがとうございます。私としては、最初に、4 をくくりだし
をくくりだし
て解く方法を想定していたんですが、別解を知ることができました。ありがとうございます。
(コメント) Renさんの解法を再現?
√(3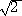 +4)=4
+4)=4
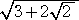 =4
=4 (
( +1)=4√8+4
+1)=4√8+4
Renさんの問題では、D=−2<0 だったので、D>0の形に持って行くには、根号の中
の の位置を逆に持って行けばよいという発想ですね!そうすれば、√
の位置を逆に持って行けばよいという発想ですね!そうすれば、√ =4
=4 で括る
で括る
という発想が決して突飛なものではなく自然な発想であるということが合点いきます。
Renさんから問題をいただきました。(平成29年4月19日付け)
平方根内に三乗根がある形です。
√([3]√(28)-3)の二重根号を外してください。([3]√は三乗根のことです。)
らすかるさんからのコメントです。(平成29年4月19日付け)
√([3]√28-3) = ([3]√98-[3]√28-1)/3
Renさんからのコメントです。(平成29年4月19日付け)
らすかるさん ありがとうございます。答えは、([3]√(98)-[3]√(28)-1)/3です。以下は想定
していた解法です。
x=√([3]√(28)-3)とすると、x^6+9x^4+27x^2-1=0 となる。また、この式の解のうち二つは
±√([3]√(28)-3)である。
ここで、x^6+9x^4+27x^2-1=(x^3+ax^2+bx+c)(x^3-ax^2+bx-c) とすると、x^3+ax^2+bx+c=0
の実数解のうち1つは、±√([3]√(28)-3) のどちらか一方である。a=1,b=5,c=-1は条件を満
たす。
x^3+x^2+5x-1=0の実数解を求めると、x=([3]√(98)-[3]√(28)-1)/3
これは、√([3]√(28)-3) に等しい。
らすかるさんからのコメントです。(平成29年4月19日付け)
私は、次のように解きました。
t=[3]√28 とします。(a+bt+ct^2)^2=t-3 とおいて、t^3=28に注意して展開整理すると、
(b^2+2ac)t^2+(28c^2+2ab-1)t+(a^2+56bc+3)=0
b^2+2ac=0、28c^2+2ab-1=0、a^2+56bc+3=0 という連立方程式を解くと、解の一つ(適解)は
(a,b,c)=(-1/3,-1/3,1/6)
これを √(t-3)=a+bt+ct^2 に代入して整理すると、√([3]√28-3) = ([3]√98-[3]√28-1)/3
Renさんからのコメントです。(平成29年4月20日付け)
なるほど、ありがとうございます。
DD++さんからのコメントです。(平成29年4月20日付け)
√(2-√3) みたいなものだと、
α=√(2-√3), β=√(2+√3) とおいて、α^2+β^2=4 と αβ=1 から (α+β)^2=6 より
α+β=√6 (α-β)^2=2 より α-β=-√2 これらを加えて2で割ると α=(√6-√2)/2
という解き方ができるわけですが、√([3]√28-3) も同様にトリオになる無理数(あるいは虚
数?)をあと2つ用意して解くことはできないものでしょうか?
Renさんからのコメントです。(平成29年4月20日付け)
根号内に虚数がはいってもいいなら、
α=√([3]√28-3)、β=√(ω[3]√28-3)、γ=√(ω^2[3]√28-3)
として、αβγ、αβ+βγ+γα、α+β+γを求めるといけます。
DD++さんからのコメントです。(平成29年4月20日付け)
√x の定義は、 x≧0 に対しては「二乗してxになる非負実数」、x<0 に対しては「i√(-x)」
なんですが、xが虚数の場合については定義されていなかったような……。
Renさんからのコメントです。(平成29年4月20日付け)
そうでしたか。α^2=[3]√(28)-3,β^2=ω[3]√(28)-3,γ^2=ω^2[3]√(28)-3 としたらいい
ですか?
DD++さんからのコメントです。(平成29年4月20日付け)
そうすると、今度はβとγが2通りずつ考えられて、α+β+γとかで、どっちを使えばいい
のかという話になります。しかも、α+β+γを計算する方針を取るとして、具体的にどうやっ
て? というのも。
Renさんからのコメントです。(平成29年4月20日付け)
β,γはどちらを採用するのかはわかりません。すみません。
βとγを共役とする。また、α>0
α^2β^2γ^2=1、α^2β^2+β^2γ^2+γ^2α^2=27、α^2+β^2+γ^2=-9
となる。βγ>0 より、αβγ=1
この解の一つは、α+β+γ=-1、αβ+βγ+γα=5 説明不足でした。すみません。
β,γの実部をかんがえたらいけそうなのですが。
(追記) 令和2年7月26日付け
最近、2重根号を外す問題に触れる機会があり、久々に考えてみた。
(参考文献) 内藤康正 著 「2重根号の計算あれこれ」 数研通信 No.97(数研出版)
問題 √(2+√6)√(√2+√6)を簡単にせよ。
(解) (2+√6)(√2+√6)
=2√2+2√6+2√3+6
=(1+2+3)+2(1・√2)+2√2・√3+2(1・√3) と考えれば、
(2+√6)(√2+√6)=(1+√2+√3)2 と式変形出来る。
よって、 √(2+√6)√(√2+√6)=1+√2+√3 である。 (終)
同様にして、次の問題も解かれる。
問題 √(8−2√13)√(4−√3)を簡単にせよ。
(解) (8−2√13)(4−√3)
=32−8√3−8√13+2√39
=(16+3+13)−2(4・√3)−2(4・√13)+2√3・√13 と考えれば、
(8−2√13)(4−√3)=(4−√3−√13)2 と式変形出来る。
4−√3−√13<0 に注意して、
√(8−2√13)√(4−√3)=−4+√3+√13 である。 (終)
(コメント) 何れも柔軟な思考力を問われる問題である。
また、一手間加えることにより、2重根号が外せる場合もあるということで、次の問題には
感心させられました。
問題 √(7√2−4√3)−√(10√2−8√3)を簡単にせよ。
(解) √(7√2−4√3)−√(10√2−8√3)
=√(7√2−2√12)−√(10√2−2√48)
=4√2√(7−2√6)−4√2√(10−2√24)
=4√2(√6−1)−4√2(√6−2)=4√2 (終)
同様にして、次の問題も解かれる。
問題 √(10+2√45) を簡単にせよ。
(解) √(10+2√45)
=4√5√(2√5+6)=4√5(√5+1)=4√125+4√5 (終)
(追記) 令和7年3月8日付け
問題 次の2重根号を外せ。
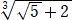
(解) 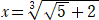 、
、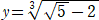 とおくと、xy=1 で、x3+y3=2
とおくと、xy=1 で、x3+y3=2
このとき、(x+y)3−3(x+y)=2 より、(x+y−
より、(x+y− )((x+y)2+
)((x+y)2+ (x+y)+2)=0
(x+y)+2)=0
(x+y)2+ (x+y)+2=0 は実数解を持たないので、 x+y=
(x+y)+2=0 は実数解を持たないので、 x+y=
よって、 x、y は、2次方程式 t2− t+1=0 の2つの解である。
t+1=0 の2つの解である。
解の公式より、 t=( ±1)/2 なので、 x>y から、
±1)/2 なので、 x>y から、
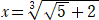 =(
=( +1)/2 (終)
+1)/2 (終)
(コメント) ( −1)/2=2sin(π/10) なんですね!
−1)/2=2sin(π/10) なんですね!
(よおすけさんからご訂正いただきました。上記は、訂正済みです。)
また、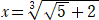 の最小多項式は、 x2−x−1 となります。
の最小多項式は、 x2−x−1 となります。
以下、工事中



