当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（平成２７年１月１日付け）
三角形 BC＝１＋
、CA＝２、∠C＝６０°を解くことにより、ｔａｎ１５°の値を求めなさい。（答） １５°の三角比の計算というと、どうしても次の図が目に浮かぶ。
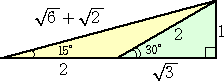
ただ、この図を用いると、どうしても２重根号の計算が避けられない。２重根号の計算を回
避する方法も知られている。（→ 参考：「２重根号」）
よおすけさんから与えられた三角形は、２重根号の計算を回避する第３の方法になります
ね！よおすけさんに感謝します。
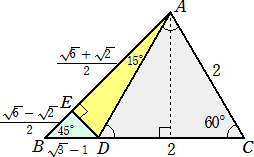
左図より、
ｔａｎ１５°＝（
−
）/（＋）＝２−
当ＨＰがいつもお世話になっているＨＮ「Ｓ（Ｈ）」さんより、別解を頂きました。
（平成２７年１月４日付け）
単位円周上の２点Ａ（１，０）とＢ（
/２，１/２）を結ぶ線分の中点Ｍ（（２＋）/４，１/４）と原点を通る直線の方程式は、 ｙ＝（２−
）ｘ である。このとき、直線 ｘ＝１ との交点は、（１，２−
）なので、 ｔａｎ１５°＝２−（コメント） Ｓ（Ｈ）さん、ありがとうございます。Ｓ（Ｈ）さんの別解を見てて次のような求め方
があることに気づきました。
ａ＝
、ｃ＝２ 、∠Ｂ＝３０°、∠Ｃ＝９０°の直角三角形ＡＢＣにおいて、∠Ｂの２等分線が辺ＣＡと交わる点をＤとおく。このとき、角の２等分線の性質から、Ｄは、辺ＣＡを、
：２に内分する点である。よって、 ＣＤ＝/（２＋）＝（２−）よって、 ｔａｎ１５°＝ＣＤ/ＢＣ＝２−
DD++さんからのコメントです。（平成２７年１月４日付け）
線分 AB を直径とする半径
の半円周上に、∠CAB=60°, ∠DAB=15° となるように２点 C、D を取り、線分 CB と線分 AD との交点を E とする。
線分 AB、BD、DA の長さを求めることにより 15° の三角比を求めよ。
※半径
なのは分数計算が出ないようにするだけの目的。半径 1/2 でやると BD と DAに直接 sin15° と cos15° が出てきます。
（コメント） 円の中心をＯとすると、∠ＡＯＤ＝３０°なので、余弦定理より、
ＡＤ2＝２＋２−４・
/２＝４−２ なので、 ＡＤ＝−１また、ＢＤ2＝（２
）2−（−１）2＝８−４＋２＝４＋２ なので、ＢＤ＝＋１よって、 ｓｉｎ１５°＝（
−１）/（２）＝（−）/４ｃｏｓ１５°＝（
＋１）/（２）＝（＋）/４ｔａｎ１５°＝（
−１）/（＋１）＝２−DD++さんからのコメントです。（平成２７年１月６日付け）
上記の（コメント）にある解法は、私の意図した手順ではありませんでした。二重根号が出
てくるので、この図の価値がなくなってしまいます。もうちょっと誘導をつけるべきでしたね。
まず、AB は直径なので、 AB＝２
△ACB は直角三角形で、 AC＝
、CB＝△ACE は直角二等辺三角形なので、 CE＝
、AE＝２よって、 EB＝CB−CE＝
−△DEB も直角二等辺三角形なので、 DE＝DB＝
−１よって、 AD＝AE＋DE＝
＋１したがって、ｓｉｎ１５°＝（
−１）/（２）＝（−）/４ｃｏｓ１５°＝（
＋１）/（２）＝（＋）/４ｔａｎ１５°＝（
−１）/（＋１）＝２−（コメント） DD++さんの問題条件とは全く真逆な図で計算していました。２重根号の計算が
出てくるので変だとは思いました．．．。今再計算してみると、なかなか味のある
図になっていますね！
よおすけさんからのコメントです。（平成２７年１月５日付け）
解答を見て、こんなに簡単にできるとは思いませんでした。僕は、以下でやっていたので・・・。
正接定理 {(BC-CA)/(BC+CA)}={tan((A-B)/2)}/{tan((A+B)/2)}・・・(1)
を使います。証明については、正弦定理から導けますので、ここではやりません。
（補足） 正弦定理から、
（ａ−ｂ）/（ａ＋ｂ）＝（ｓｉｎＡ−ｓｉｎＢ）/（ｓｉｎＡ＋ｓｉｎＢ）
＝ｃｏｓ｛（Ａ＋Ｂ）/２｝ｓｉｎ｛（Ａ−Ｂ）/２｝/ｓｉｎ｛（Ａ＋Ｂ）/２｝ｃｏｓ｛（Ａ−Ｂ）/２｝
＝ｔａｎ｛(A−B)/2)｝/tan｛(A＋B)/2)｝ （終）
右辺より、A+B=180°-C=120°から、tan((A+B)/2)=
左辺より、{(BC-CA)/(BC+CA)}={(
+1-2)/(+1+2)}=(-3+2)/3(1)より、
{tan((A-B)/2)}=tan((A+B)/2)×{(BC-CA)/(BC+CA)}=
×(-3+2)/3=2-・・・(2)2-
≒0.2679 なので、三角関数の表より、{(A-B)/2}≒15°(2)より、 tan15°=2-
（コメント） 何となく計算が遠回りしているような雰囲気かな？
よおすけさんからのコメントです。（平成２７年１月６日付け）
元々、正接定理(ネイピアの法則)の応用として出したのが本問題です。Wikipediaの「正接
定理」-「応用」を見て、つくりたい！と思い、出しました。正接定理のことをもっと知って欲し
かった、というのもありましたが、問題自体がtan15°の値に辿り着くまでの解法というイメ
ージが強すぎて、目立たなくなってしまったことに戸惑っています。正接定理は、また別の形
で投稿したいと思っています。
らすかるさんからのコメントです。（平成２７年１月５日付け）
一辺が２の正方形ABCDの内部に正三角形EBCを作り、ADの中点をMとすると
AM=1、ME=2-
だから、tan15°=ME/AM=2-（コメント） らすかるさんの解がとてもエレガントですね！今日偶然にも、折り紙を折って１５°
を作るという問題を考えていて、らすかるさんのアイデアを復習したばかりです！
円に内接する四角形の性質から、∠ＭＡＥ＝１５°は明らかですね。
よおすけさんから解答をいただきました。（平成２８年７月１９日付け）