意外な疑問 　　　　　　　　　　　　　

　このページは、関西在住のある高校生からのメールがきっかけとなり、企画されました。

<<　目　次　>>

（１）	三角関数補角の公式	（２）	三角形の面積	（３）	負の数の計算
（４）	一次方程式	（５）	計算の省略	（６）	１次不等式の解法
（７）	２次関数のグラフ	（８）	平方完成	（９）	平方完成の回避
(10)	三角比の定義	(11)	分数の足し算	(12)	和積の公式の回避
(13)	累乗の記号	(14)	凹凸の判断	(15)	分数の通分
(16)	平方完成(2)	(17)	三角比の覚え方	(18)	ａ の０乗
(19)	正接の公式	(20)	小数部分	(21)	剰余の定理
(22)	正弦定理の計算	(23)	面積の計算	(24)	関数の極限
(25)	三角比の覚え方(2)	(26)	三角比の覚え方(3)	(27)	分母の実数化
(28)	対数表現	(29)	０！＝１	(30)	負×負＝正
(31)	複素数の変形	(31)	三角形の合同条件	(32)	比の記号
(33)	ｙ切片

平成１４年１０月４日
　三角関数の公式に、 　 ｓｉｎ(１８０°−θ)＝ｓｉｎθ
　　　　　　　　　　　　　　　 ｃｏｓ(１８０°−θ)＝−ｃｏｓθ
　　　　　　　　　　　　　　　 ｔａｎ(１８０°−θ)＝−ｔａｎθ
というものがある。この公式の例題として、次のような解き方を説明すると、生徒は怪訝な
顔をする。

　どうも生徒は、１２５°＝１８０°−５５°という発想が苦手らしい。（教える側にとっては、
ごく自然な変形だと思うのだが・・・・？）
　これに対して、次のような計算を示すと、「分かった！」という顔をする。

　　θ の補角を頭の中で計算し、それを１８０°から引いてから公式を使うよりも、公式を先
に使って後はゆっくり式計算を楽しむという方が、生徒にとっては分かりやすい解法のよう
である。


平成１４年１０月９日
　（高校３年生　Ｋ．Ｋ．君からの投稿）

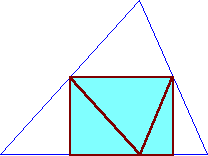小学校の算数の時間、先生が「三角形の面積をどう 　　やって求めるか？」という問題を出した。 　　　普通この場合、同じ三角形を２つ並べて平行四辺形 　　を作り、三角形の面積を平行四辺形の面積に帰着さ 　　せて求めるという方法で、説明される。 　　　僕は、長方形の面積は分かるが、三角形の面積は 　　よく分からなかった。そこで、三角形を書いた紙を切 　　り取り、三角形の２辺の真ん中を結ぶ折れ線で折り 　　返し、さらに、左右の頂点が今折り返した頂点に重な 　　るように折り返して、小さい長方形を作った。その面 　　積を２倍して、三角形の面積を求めた。 　　　このことを先生に話したら、褒めてくれた。

　負の数を含む計算に関して、３人の方から投稿をいただきました。負の数の計算は、中
学校に入っての最初の難関ですが、皆さん各自工夫されて克服しているようです。

　（高校３年生　Ｅ．Ｈ．君からの投稿）
　　中学生の頃、「引き算で分からなくなったら、数字の差はいくつかを求めろ」といわれた。
これに対して僕は次のように考えた。
　　例えば、５−７ の計算で、まず、７ と ５ の差２ を求め、７が５になるには、あと−２ が
必要ということで、その−２ が答になる。
　　この考え方は、自分にとって、とても役に立った。

　（高校３年生　Ｔ．Ｓ．君からの投稿）

　　　　　

　５−７ という計算は、確か学校では、７ から５ を引いて、マイナスを付ければよいというよ
うに教えられたが、当時はよく理解できなかった。自分で数直線を思い浮かべ、５ から１ず
つ７回左へ移れば、−２ になると考えると、分かりやすく答が出た。

　（高校１年生　Ｙ．Ｍ．君からの投稿）
　　中学のとき、正負の計算で先生はやり方だけ教えたけど、よく分からなかった。家に
帰って、例えば、−５＋２ のような計算を、数直線を書いてやったら分かるようになった。
−５ から、右の方へ ２ だけ移動すれば、３ という答になるということが実感できた。


平成１５年　３月　９日
　（私の同僚　Ｋ．Ｉ．さんからの投稿）

　授業で上記のような計算で方程式を解くと、「はてな？」という顔をする生徒は少なくない。
小学校の算数の時間のように、次のような説明をすると、生徒は、「わかった！」という顔
をする。

６Ｘ を、「６かけるＸ」という認識で計算したものが前述のもので、６Ｘ を、「Ｘ を６個加えたも
の」という認識で計算したものが後述のものである。やはり、掛け算で考えるより、足し算
で考えた方が分かり易いのかもしれない。もっとも、掛け算をプログラミングするとき、足し
算がベースになるので、生徒の認識もあながち不自然とは言えない。（こちらを参照）


平成１５年　３月１１日
　（高校２年生　ｓｈｉｎ（ﾊﾝﾄﾞﾙﾈｰﾑ）君からの投稿）

　数学の先生というと、途中計算を端折る傾向がある。例えば、

としがちだが、生徒の側からは、分かりづらいという。途中計算のカラクリを確認しながら、
計算を進めると、生徒にとっては理解しやすいようだ。

　少しの労力で、生徒の理解が進めば、これほど嬉しいことはない。


平成１６年　９月　９日
　新学習指導要領において、中学校での不等式の扱いは軽減され、高校になって初めて
本格的に不等式の理論を学習するといっても過言ではない。

　不等号という記号も、単なる記号としてしか扱われないので、不等式の扱いも形式的に
ならざるを得ないのが実状である。

　今まで、不等式の解法というと、次のように解いてきた。

　ただ、この解法だと、両辺を負の数で割るときに、不等号の向きが反対になるということ
を覚えておく必要があり、等式の場合との違和感を感じる原因にもなっているようだ。

　割る数の正負を気にしないで済むようにするには、常に、Ｘの係数が正になるように移項
することを考えればよい。最近、次のような解法があることを知った。

　どちらが分かりやすいかは、人それぞれだろう。生徒たちに聞いてみても、それぞれを
支持する声があった。

　私的には、どうも「２＜Ｘ」という書き方に違和感を持ってしまう。

「Ｘ」を主語ととらえ、「Ｘは２より大きい」は、やはり、「Ｘ＞２」と表現したい。英語のＳＶＣ
の順序を重視する立場である。それに対して、「２＜Ｘ」は、答えとしてはあっている訳で
あるが、読み方が、どうしても「２はＸより小さい」となってしまい、「２よりＸは大きい」とは
読みづらい。数直線での ２ と Ｘ の位置関係から、「「２＜Ｘ」が支持されているようだ。

　２次不等式　(Ｘ−１)(Ｘ−３)＞０　を解く場合も、解 Ｘ を主語ととらえ、Ｘ＜１、Ｘ＞３　と
書いてきたが、この書き方は、最近の教科書からは淘汰されつつある。

　現在、数直線でのＸの位置を考えて、「Ｘ＜１、３＜Ｘ」とする書き方が主流で、「Ｘを主語
としない」形式的な記号化が進んでいる。

　果たして、このような不等式の扱いは、その後の数学の理論展開に支障はないのだろ
うか？支障はないとしても、多少違和感を持つのは私だけだろうか？


　ＭＤＡさんからのコメントです。（平成２６年９月２９日付け）

　負の数で割りたくない私なら、こう書きます。

　３ｘ＜５ｘ−４　より、　４＜５ｘ−３ｘ　すなわち、　４＜２ｘ　より、　２＜ｘ

　よって、 ｘ＞２

　場合分けの表記も教科書の

1)　１＜ｘ　　2)　０≦ｘ≦１　　3)　ｘ＜０　　になじめなかったので、私はこう書いています。

1)　ｘ＞１　　2)　０≦ｘ≦１　　3)　ｘ＜０


　DD++さんからのコメントです。（平成２６年９月２９日付け）

　２＜ｘ　は確かに、　ｘ＞２　と、ｘを左辺に持ってきますね。しかし、場合分けの表記につい
て、私は前者にも多少違和感はありますが、後者はさらに違和感があります。

　複数の不等式が揃って初めて意味をもつような場合は、多くの人は数直線（またはそれと
等価なもの）上で範囲の関係を理解します。ですから、そういう類の不等式は不等号の向き
が統一されていないと読みにくいんですよね。

1)　ｘ＜０　　2)　０≦ｘ≦１　　3)　１＜ｘ　　なら全実数を網羅していることはすぐに読み取れま
すが、ＭＤＡさんのだと、パッと見ただけじゃ重複も漏れもないことは整理しながら読まないと
わかりませんよね。


　Ｓ（Ｈ）さんからのコメントです。（平成２６年９月３０日付け）

　場合分けの表記も教科書の表記が、

1)　ｘ∈(1，∞)　　2)　ｘ∈[0，1]　　3)　ｘ∈(-∞，0)　　R=(-∞，0)∪[0，1]∪(1，∞)

なら全然違和感はありません。


平成１６年１０月　７日
　いま日本の多くの高校において、１年生では「２次関数」を学習していると思う。その中
で、次のような計算の正解率が極端に悪いということを実感している方はいないだろうか？

　この計算は、２次関数のグラフを書いたり、ｙ 軸との交点を求める際に必ず現れるもの
であるが、意外にも正しく計算できない生徒が少なからず存在する。

　上記の計算の肝要なところは、（−１）² の処理の部分である。これを、−１²　と勘違い
して、−１ とするようだ。ある調査によると、（−１）² と −１²　の区別が出来ない生徒は、
２割程度いるらしい。

　生徒は、括弧の使い方に無頓着だ。たとえば、３と−４をかける場合、平気で、３×−４
としてしまう。ここは、やはり、しっかり　３×（−４）と指導していきたい。

　このような計算力不足を補うかのように、中学校の教科書も変化しているようだ。

　２次関数のグラフを書く場合、これまで例えば次のような対応表を作らせてきた。

　この流れで、高校でも対応表を計算させ、 ｙ＝２(ｘ−１)²＋２　のようなグラフを書かせて
きた。しかし、どうも教科書を見ると、このような教え方は旧式らしい。教科書では、確かに
最初の方では対応表を用いて説明しているが、主流は平行移動の考えである。あたかも
生徒の計算力不足を見透かしたかのような対応になっている。

　生徒にあまり計算をさせまいと、中学校の教科書でも、次のような雰囲気になっている。

　上記では、原点から ｘ の値が １ ずつ増えると、１、３、５、７、・・・　と ｙ の値が増えていく
ということを言いたいようである。この性質は、　ｎ²−（ｎ−１）²＝２ｎ−１　から、明らかであ
ろう。

　この ｙ の変化量に注目するという視点は、グラフを書く場合に次のように反映される。

　　　　　　　　　

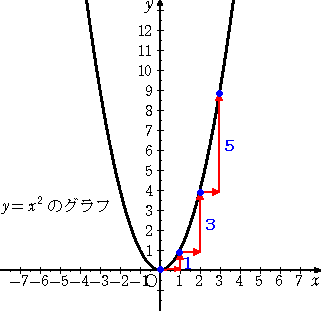
　すなわち、原点から １ ずれるごとに、１、３、５、７、・・・　と点を目盛っていけば、それらし
い２次関数のグラフが書けてしまう。もう、ｘ² の計算は必要ないくらいだ。
　もし、関数が、ｙ＝２ｘ²　ならば、それぞれ２倍して、２、６、１０、１４、・・・　と考えればよい。

　高校で、実際にこのような教え方をされている方がおられて、ある程度の成果をあげてい
ると聞く。でも、はたして、このようなグラフの書き方で本当に関数の意味が分かったといえ
るのであろうか？グラフが書けただけで、そのグラフを使って、関数を読み取ることは可能
なのだろうか？今度その方に会う機会があるので、質問してみようと思う。


平成１６年１０月１７日
　「２次関数」の学習で、「平方完成」という式変形は、２次関数の一般形を標準形に処理す
る上で避けて通れない計算である。
　中学校では解の公式を教えなくなった分、この「平方完成」という方法を使って、問題練習
する機会が増えたと思うのだが、生徒の定着率は、驚くほど低い。

　平方完成は、分かってしまえば何でもない計算であるが、生徒にとっては、分かるまでが
非常に辛い計算であるようだ。

　教科書では、平方完成は次のような式変形で教えられる。これは、中学校での２次方程
式の解法を意識した式変形である。

　それに対して、次のような教え方もある。（この場合は「 ｘ の係数の半分」ということを呪文
のように唱える。）

　私自身は後者の方法を採用することが多いが、どうも、このような式変形は、計算が不得
手な生徒には大海をさまようように感じるらしい。かといって、教科書のような教え方が分か
りやすいとも言えない。生徒に聞くと、後者の方が分かりやすいと言う。２次関数を教えると
きはいつも、今年はどちらで教えようかと悩みは尽きない。全国の皆さんも、同じ悩みを抱え
ていませんか？

　　（追記）　平成２１年９月１２日付け

　　　　　　「 ｘ の係数の半分」ということを呪文のように唱えれば、平方完成も容易に会得さ
　　　　　れるが、この方法にも意外な落とし穴がある。

　　　　　　ｘ の係数が偶数の時は瞬時に答えられるのに、奇数の時は何故か詰まってしまう。

　　　　　　例えば、「 ｘ²＋３ｘ 」を平方完成する場合何故かしら、３/２ が直ぐには出てこない。
　　　　　それでも、「１．５」という声が聞こえてくるのだが、何となく自信なさそう．．．。

　　　　　　そうなのだ！彼らは分数よりも小数の方がお好きなのだ！比が苦手な今風の高
　　　　　校生が、比として表される「３/２」よりも実体として感受できる「１．５」の方を好むの
　　　　　だ。

　　　　　　そんなわけだから、「（１/２）ｘ²＋ｘ を平方完成せよ。」なんて言われたら、彼らは
　　　　　もうパニックである。何とかこのパニックを治める良薬はないものだろうか？

　　（追記）　平成２２年８月　８日付け

　　　　平方完成の公式　ｘ²＋２ａｘ＝（ｘ＋ａ）²−ａ²　について、タイルを用いた説明を、松
　　　山在住の Ｔ．Ｙ．さんよりご教示いただいた。

　　　　　　　

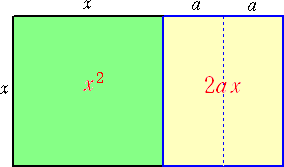
　　　という図形を切り貼りして、正方形（面積 （ｘ＋ａ）²）を作ろうとすると、小正方形（面積
　　　ａ²）が不足する。

　　　　　　

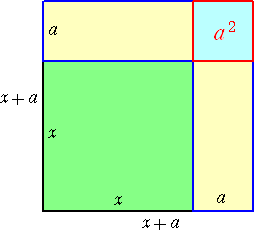
　　　だから、　ｘ²＋２ａｘ＝（ｘ＋ａ）²−ａ²　が成り立つ。


平成１６年１０月２４日
　平方完成も、　ｘ²＋４ｘ のような基本形がやっと出来るようになった生徒にとって、その応
用形である、たとえば、　２ｘ²＋４ｘ　のような平方完成になると、極端に難しく感じるらしい。

　その理由は明らかである。生徒は、次のような計算ミスをしがちである。

　今の生徒の行う計算の特徴として、括弧の使い方が不得手である。だから、−５² のよう
な計算も、２５と誤答する割合は高い。

　このような生徒の計算力を考えると、平方完成を教え込むことは無意味のように感じる。

結局のところ、平方完成させることによって、放物線の軸の式と頂点の座標が求まればい
いわけで、次のような回避策が考えられる。

　教科書の順番から言えば、２次関数の学習の前に２次方程式を学習しているので、道具
として、２次方程式の解法が使える。

放物線　ｙ＝２ｘ2＋４ｘ　の軸の式と頂点の座標を求めよ。 　　　　　２ｘ2＋４ｘ＝２ｘ（ｘ＋２）＝０　より、　ｘ＝０，−２ 　　　ｘ2 の係数２は正の数なので、グラフは下に凸であり、 　　上の計算から、グラフは、ｘ 軸と、２点（０，０）、（−２，０）で交わる。 　　　放物線は、軸に関して線対称なので、 　　　２点（０，０）、（−２，０）の中点（−１，０）を通り、 　　　ｙ 軸に平行な直線 ｘ＝−１　が軸の式となる。 　　　　また、頂点は、軸の上にあるので、 　　　ｘ＝−１　から、ｙ＝−２　となり、 　　　頂点の座標は、（−１，−２）である。

　もちろん、微分法を知っていれば、もっと簡単に軸や頂点を求めることができる。果たし
て、平方完成は、微分法の学習までの「つなぎ役」なのであろうか？


平成１７年　２月２６日
　数学を教えていられる方が、共通に多分感じている今の生徒の弱点をあげるとすれば、
計算力そのものであろう。特に、比の計算が苦手なようである。

　たとえば、比として、「 １ ： ２ 」 ということは理解できても、比を、「 １/２ 」と表したりする
と、突然、拒否反応を示す場合が多い。

　教科書では、三角比の定義そのものが分数表示の比で定義されるので、小学校・中学
校で普通にできていた比の計算が、全く違う種類の計算と映るようで、計算の手が止まっ
てしまう。

　三角比の定義の導入そのものを見直す必要がありそうだ。

　「取れたて通信」の中の記事で、宮本次郎（釜石南高校）さんが次のような導入を考えてお
られる。

斜辺の長さが １ の直角三角形において、 　　　　　対辺の長さ ＝ ｓｉｎ θ　　底辺の長さ ＝ ｃｏｓ θ 　　　　と書くことにする。

　この導入により、今までの三角比の定義が、小学校・中学校の比の定義の延長線上に
自然に組み入れられるのではないだろうか。

左図において、　　ｙ ＝ ｒ・ｓｉｎ θ　　ｘ ＝ ｒ・ｃｏｓ θ 　　　なので、　　　ｓｉｎ θ ＝ ｙ/ｒ　　　ｃｏｓ θ ＝ ｘ/ｒ 　　　と書ける。

　実際の応用の場面では、三角比の定義そのものよりも、むしろ、

　　　　　　　　　　ｘ ＝ ｒ・ｃｏｓ θ　、　ｙ ＝ ｒ・ｓｉｎ θ

を直接使う場合がほとんどである。無理をして、分数の比で三角比を教えないで、上記の
形で教えた方が生徒にとっても負担は少なくなるかもしれない。


（追記）　平成２８年８月７日付け

　８月６日（土）、日本大学文理学部数学科のサマースクールが百周年記念館で開催され、
参加してきた。記念館入り口にはリオ五輪に出場する日本大学の学生・卒業生のパネルが
掲示されていて、その多さに圧倒された。

　何森　仁先生の「こどもと楽しもう！学校数楽」でも上記話題が取り上げられていた。

すなわち、傾斜角θの坂道を車が１ｍ移動するとき、何ｍ上ったかを「ｓｉｎθ」、何ｍ右に進

んだかを「ｃｏｓθ」で表せば、車が坂道を ｒ ｍ移動したら、

　車は、　ｒ・ｓｉｎθ　だけ上ったことになり、　ｒ・ｃｏｓθ　だけ右に進んだことになる。

　このように考えると、θが鈍角の場合、何故「−ｒ・ｃｏｓθ」となるかも簡単に説明できる。

　即ち、鈍角の坂を車が進むとき、

　車は、　ｒ・ｓｉｎθ　だけ上ったことになる。（これは、θが鋭角の場合と同じ）

　さらに、車は、　ｒ・ｃｏｓθ　だけ左に進んだことになる。右方向を正の向きとしているので、

左方向には「−」が付くというわけである。

　何森先生は黒板上で車を自動で走らせたが、その車が欲しくなった。どこで売っているの
だろう？何森先生は、欲しいと言われてもあげませんというのだが．．．。

　この考え方でいくと、　ｓｉｎ９０°＝１、ｃｏｓ９０°＝０　の説明も容易である。

　即ち、傾斜角９０°の坂道を車が１ｍ移動するときに何ｍ上ったかは当然「１」だし、何ｍ
右に進んだかは「０」となる。

　何森先生の「三角比は坂、三角関数は観覧車」という言葉が印象的でした。


平成１７年　５月２３日
　分数の足し算というと、私は次のように計算してしまう。

　でも、このような計算は、計算力が不確かな生徒にとって評判は芳しくない。次のように
計算すると納得するようだ。

　２つの計算に大きな違いはないように思うが、生徒にとっては大きな壁が２つあり、それ
を一気に計算しているので分かりにくいようだ。

　（壁その一）　共通の分母（５４）を発見して、それぞれを通分すること。
　（壁その二）　分母が同じ分数同士の足し算。

　２つの壁のうち、最初のものが一番困難さを感じるようだ。それが何故なのか、今まで気
がつかなかったが、その理由がようやく判明した。

　平成１７年５月２１日放送の「世界一受けたい授業！！」（ＮＴＶ系　土曜夜７時５７分〜８時５４分）
で、百ます計算で有名な陰山英男さんが明解に答えられていた。

　今の小学校では、上記のような計算を機械的に求める方法を教えてはいない！

番組では、次のような機械的な計算方法を紹介された。
　　　　　　　　　　　　　（この方法は昔から知られている方法らしい。）

　この方法は、最小公倍数を求める方法を巧妙に利用している。でも、分かりやすいことは
確かだ。今度、通分が苦手な生徒に、この方法をこっそり教えてみよう！


平成１７年１０月　１日
　「数学ＩＩ 」で三角関数の加法定理を学ぶが、その周辺は公式の嵐で、なかなか定着しな
い分野である。私自身の経験からも三角関数の微分積分で練習を積んで、ようやく様々な
公式（倍角・半角・３倍角・和積・積和・単振動の合成等）が身に付いたように思う。

　授業時数の減少の影響で、じっくり練習する時間が確保されないまま、通り一遍の話で
終わっているというのが、日本全国共通の悩みなのではないだろうか？

　その学習状態で進級し、「数学ＩＩＩ 」で三角関数の微分を学習する段になって、今までの
積み残しによる問題が一気に噴出する。

　教科書では和積の公式を用いて、ｓｉｎθの微分の公式を証明している。一昔前だったら、
大抵の生徒は和積の公式等を覚えていて円滑に証明が進んだものだが、最近は、定着
率が低いので現地調達方式風に再度説明を補足しないと授業が進まないというのが実
状だ。そこで授業の流れが止まってしまうわけで、かえって授業をわかりにくくしてはいな
いかと危惧するばかりである。

　そこで、和積の公式を用いないで、ｓｉｎθの微分の公式を証明しようと思い立った。生徒
たちは、和積の公式は覚えていなくても加法定理は何とかおぼろげながら覚えているよう
なので、加法定理と極限の計算で乗り切れるものと判断した。

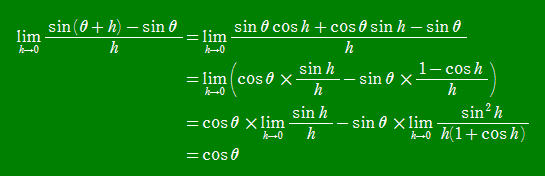　この証明方法が教科書の証明に対して、どれくらい分かりやすくなったのか、または分か
りにくくなったのか、是非他の方のご意見を伺いたいものだ。（メールは、こちらまで）


平成１７年１２月　６日
　「数学ＩＩ 」で学ぶ学習項目の中で「三角関数」の定着率が悪いのはよく知られているが、
それに匹敵するぐらい悪いと感じるのは「指数・対数」である。

　生徒が、なぜ上記のような計算ミスをするのか、よく考えてみると、やはり「２³」といった累
乗の書き方に原因があるのだろうと思う。

　この累乗の記号は慣れてしまえば便利な記号であるが、初学者がノートに取る際、よほど
注意しないと、「２³」を「２３」と書き誤って、「２³」を「２×３」と勘違いしたまま覚えてしまったり
もしくは、「２³」を「２×２×２」と計算するよりも「２×３」と計算する方が楽なので意図的にそ
う覚えてしまったりしているのではないだろうか？

　インターネットの世界では、「２³」を「２＾３」と書く慣わしになっている。このように、指数「３」
を何らかの形で強調しない限り上記のような計算ミスを根絶することは難しいだろう。

　そこで、私は、累乗の記号「２³」を、

などと書くことを提案したい。このような形の記号を用いると、

という忘れやすい式も

となり、「左辺のｅｘｐを右辺に持って行くとｌｏｇに変わる」という単純な図式になるのだが？

　これについて是非他の方のご意見を伺いたいものだ。（メールは、こちらまで）

（追記）　平成２２年８月６日付けで、松山在住のＴ．Ｙ．さんよりメールにてご意見を頂いた。

　２³＝ｅｘｐ₂３　と表せば、対数との対応は分かり易くなるかもしれませんが、結局、２³　の
分かり易さがなくなって、指数も対数も難しいものということになると思います。

　ａ^ｘ＝Ｎ　は、ｘ＝ｌｏｇ_ａＮ　と同等といくら言っても、記号 ｌｏｇ のために対数が分からないと
いう学生が２０％くらいはいるように思います。

　だから、ｅｘｐ₂３　の ｅｘｐ という記号のために分からないと拒否反応を起こす生徒や学生
が目に見えるようです。

　因みに、私は、　ｘ＝ｌｏｇ_ａＮ　を対数表示といい、ａ^ｘ＝Ｎ　を指数表示と言っています。（同
じものの違った表現ということで。）

　ｌｏｇ で表した表現が難しいのならば、指数表示に帰ればいいだけの話のように思います
が、それでもなかなか理解をしてもらえない。当然ですが、対数関数は対数表示で表し、
指数関数は指数表示で表されていると教えます。

　学生に難しいのは、上の指数表示と対数表示が同じだといった後で、対数関数と指数関
数は逆関数だと教えられることもあるでしょう。

（コメント）　Ｔ．Ｙ．さん、ご意見を頂きありがとうございます。私もＴ．Ｙ．さんと同様に、「対数
　　　　　　表現」とか「指数表現」という物言いをして両者は同じことであることを強調するよ
　　　　　　うにしています。
　　　　　　　ある研究授業で、対数関数のグラフを描かせるとき、計算をすべて指数表現に
　　　　　　直させてから計算させている方がおられました。私自身これまで ｌｏｇ₂１ や ｌｏｇ₂２
　　　　　　や ｌｏｇ₂４ など対数表現のままで計算させるものと思っていたので、まさに「目から
　　　　　　鱗」でした。そのような計算を通して逆関数の概念を身につけるのかなと感心した
　　　　　　覚えがあります。


平成１８年１月２３日
　「数学ＩＩＩ 」で学ぶ学習項目の中で、曲線の概形を描く問題は一つの山場だろう。そこでは、
「数学ＩＩ 」で学んだことよりも深い理論で、より詳しいグラフが描かれる。

　その際、次の公式が用いられる。

　ｆ’(ｘ) の増減で ｆ(ｘ) の凹凸を考えればいいわけだが、なかなかこの理論は生徒にとって
難関なようだ。

　この公式に対して、高校３年生の　Ｎ．Ｔ．君が斬新な早わかり記号を考案してくれた。

　ｆ(ｘ) が単調増加であることは、矢印の記号を用いて、「↑」と表される。単調減少ならば、
「↓」である。

　ｆ”(ｘ)＞０　ならば、ｆ’(ｘ) は単調増加であるが、このとき矢印「→」を、ｆ’(ｘ) の矢印の下側
に書く。

　ｆ”(ｘ)＜０　ならば、ｆ’(ｘ) は単調減少であるが、このとき矢印「→」を、ｆ’(ｘ) の矢印の上側
に書く。

　そうすると、ごく自然に曲線の凹凸が浮かび上がってくるから不思議だ。このような矢印の
記号による凹凸の判断の簡便法は私にとっては初見の事柄である。皆さんにも普及させた
いので、記号をまとめて整理しておこう。

ｆ’(ｘ)＞０、ｆ”(ｘ)＞０　の場合 ｆ’(ｘ)＞０、ｆ”(ｘ)＜０　の場合 単調増加で、下に凸 単調増加で、上に凸 　 　　 ｆ’(ｘ)＜０、ｆ”(ｘ)＞０　の場合 ｆ’(ｘ)＜０、ｆ”(ｘ)＜０　の場合 単調減少で、下に凸 単調減少で、上に凸

　上図で、黒矢印が第１次導関数　ｆ’(ｘ)　のもの、青矢印が第２次導関数　ｆ”(ｘ)　のもの
で、一方の始点から他方の終点に向かうように赤矢印（円弧）を描けばよい。

　一方の始点から他方の終点に向かうように矢印を描くとき、円弧になる場合はただ一つ
の場合しかないので、上記の記号で確定される。


平成１８年７月　２日
　算数・数学における計算技術で、「通分する」ということは必須の技法だと今まで思って
きたが、生徒たちにとってはすんなり受け入れるだけの余裕がないのか、通分することに
非常な時間を要することを度々経験する。

　たとえば、次のように計算すると、生徒は怪訝な顔をする。

　少し途中を補って、次のように計算すると、「分かった！」というような顔をする。

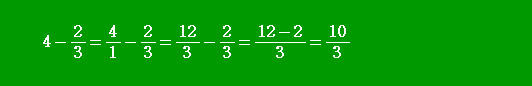　教える方としては「暗算でできるだろう．．．。」と思うのだが、生徒にとって通分することは
思いの外難解な計算に映るようだ。


平成１８年１０月１９日
　２次関数の一般形を標準形に処理する上で避けて通れない計算ということで、「平方完成」
の話題を、平成１６年１０月１７日付けで取り上げたが、やはり生徒にとって「平方完成」は難
しい計算と映るようだ。
　平成１６年１０月２４日付けの「平方完成の回避」では、ｘ 軸との交点の ｘ 座標を利用する
方法を取り上げたが、決定力には欠けるように思う。
　ここは、下記のような公式を天下り式に与えて計算させる方が生徒にとっては負担が軽い
のかな？と最近思うようになった。

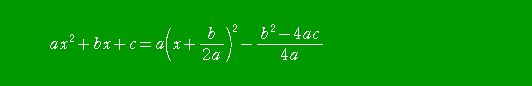　具体的には、次のように計算を行う。

　「このような式変形はどう？」と教え子に尋ねると、「こっちの方が簡単かな？」との声。教
科書における解法やこれまでの教え方のことを考えると、何か複雑な心境？！

　実のところ、私自身は高校生の時からこちらの方で平方完成しているので全く違和感は
ないのだが、読者の方はどうなのだろう？

　（追記）　平成１８年１２月１７日付けで、ＨＮ「ｍａ−．」さんよりメールを頂いた。

　　「ｍａ−．」さんは、平方完成の問題は、基本的にすべて２次関数として扱うそうである。
　これは、関数の値が求められるようにするための工夫とのこと。

　　上記の例で　ｙ ＝ ２ｘ² ＋４ｘ−３　とおく。

　　まず、上記の解と同様の計算で、　２（ｘ＋１）²　を求めさせる。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（この求め方は、暗記させるとのこと。）
　黒板には、

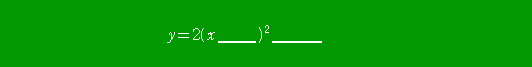　と書いて、随時書き込み可能な状態にして、生徒に空所を埋めさせるそうである。

　　後半の計算は、上記のような煩雑な計算はパスして、直接的に次のように求めさせる
　のだという。

　　放物線の頂点の ｘ 座標が −１　ということが分かったので、

　　ｙ ＝ ２ｘ² ＋４ｘ−３　に、ｘ＝−１　を代入して、　ｙ＝２−４−３＝−５

　これより、　ｙ ＝ ２ｘ² ＋４ｘ−３　＝　２（ｘ＋１）²−５

　（コメント）　とてもスッキリした解法で、分かりやすいですね！今度教えるときには、この
　　　　　　　方法で試してみたいと思います。「ｍａ−．」さんに感謝いたします。

　　　　　　　　「ｍａ−．」さんによれば、中位〜低位のクラスで定着率はかなり上がったそ
　　　　　　　うである。この式変形をした「後」が重要なので、天下り式でもよいのでは?　と
　　　　　　　のこと。私もこの考えに賛成で、式変形で挫折することなく放物線の美しい性
　　　　　　　質を生徒全員に見させたいですね！

　（追記）　平成２１年９月１２日付けで、ＨＮ「ＧＡＩ」さんよりご教示頂きました。

　　「ＧＡＩ」さんによれば、初めて習う高校一年生に機械的に作業する方法として採用したら、
　以外に簡単に、どんな場合でも確実に変形できるようになったとのこと。ある手順として作
　業させるように指導するといい結果になるそうである。

　　その機械的な作業方法とは、

　この作業をマスターさせれば、ｂ が奇数だろうが、ａ が分数だろうがスイスイ変形していく
とのこと。

（コメント）　ＧＡＩ さん、ありがとうございます。今度試してみたいと思います。


平成１８年１２月１５日
　三角比の定義の覚え方には幾つかの種類がある。

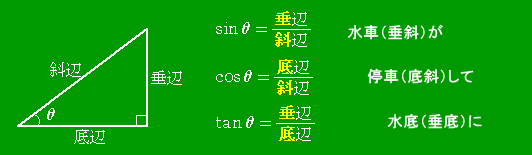というものや

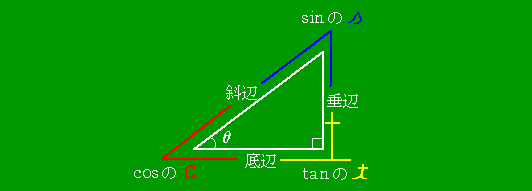というものなど。

　私の高校時代、後者の方が覚えやすいと思ったので、生徒にもこちらの覚え方をすすめ
るのだが、評判は今一歩である。なぜか古風な前者の方で覚えている生徒の方が断然多
い。とても不思議に思う今日この頃である。

　三角比の学習の後半の方では、たくさんの公式が怒濤のように押し寄せてくるが、後者
で覚えた方が、公式をスムーズに覚えられるのだが．．．！

　前者で覚えた生徒は、それらの公式をどうやって覚えるのだろうか？少し不安である。三
角比の公式の定着率が非常に悪いが、もしかしたら、ここら辺にその遠因があるのかもし
れない。

（追記）　平成２５年９月６日付け

　上図で、「垂辺」のことを「対辺」ともいう。このとき、次のような覚え方があることを最近知
った。

　　　サイン（sin）は、大変（対辺）

　分母は斜辺ということは分かっているが、分子が「垂辺」なのか「底辺」なのか、なぜか迷う
生徒も多い。そのときの呪文にでも使えるかな？


平成１９年１月４日
　今日は仕事始め。冬休みももうすぐ終わる。休み明けで一番危惧されるのは、せっかく学
んだことを休み中どこかに置き忘れてしまい、すっかり初期状態に戻ってはいないかという
点だ。そういう生徒には、「新しいことを覚えるには、古いことを忘れることも必要だね！」と
互いに慰め合うことにしているのだが．．．。

　数学を暗記で乗り切っている生徒に特にその傾向が強い。その場は理解して使いこなせ
ても、時間とともに忘れ去られていくということは、やはり理解の仕方、させ方に問題がある
からだろう。

　たとえば、「　ａ⁰＝１　」という約束は、覚えやすいのか、最初「０」だと言い張っていた生徒
も、いつしか「１」で納得したかのように、その単元を練習している間は、ほとんど間違えるこ
とはない。しかし、違う単元で、「　ａ⁰ は？　」と突然聞いてみると、「０」と答える割合がなぜ
か増える。

　自然数 ｎ に対して、　ａ^ｎ　を、「ａ を ｎ 個掛け合わせたもの」と定義して、　今まで、ａ⁰ の
値を次のように説明してきた。

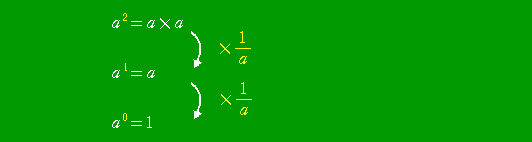　指数が１減ることは、ａ で割ることに相当することから、「　ａ⁰＝１　」という約束を説得して
いるわけだが、やはり、ａ^ｎ　を、「ａ を ｎ 個掛け合わせたもの」としている以上、「　ａ⁰　」の
釈然としない位置づけは拭い去れないようである。それが、定着率の悪い遠因になっている
ように感じる。

　これに対して、筑波大附属高校の山田研也先生が、著書「高校数学と仲直りブック」（技術
評論社刊）において、ａ^ｎ　の定義を、

　　　　１に、ａ を ｎ 回掛け合わせたもの

としてはどうかと提言されている。

　このように定義すると、あまりしっくりこなかった「　ａ⁰ 　」が、明確な位置づけとなって紛れ
がないように思う。

　すなわち、　ａ² は、１に、ａ を２回掛け合わせるので、１×ａ×ａ　だし、ａ⁰ は、１に、ａ を ０
回掛け合わせるということは、１に何も掛けないということで、１　そのものだし、上記のような
技巧的な説明は不要になる。

　また、このように定義すると、上記と同様な説明を要した「　ａ^−ｎ　」が、次のように理解さ
れることは自然だろう。

　これで、定着率の悪い

　　　　　　

という計算規則も自然に身に付くものと思われる。来年度実際に実践し研究してみたい。


平成１９年３月３日
　もうすぐ年度も終わり、数学�Tの学習もまとめの時期になった。生徒と一緒に「三角比」の
所を復習しているとき、何やら見慣れない図式をノートに書いている女生徒がいた。

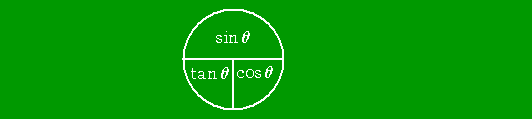　これは、正接の公式（正弦・余弦・正接の関係）

　　　　　　　　　　

を図式化したもののようであるが、このように図式化すると、

　　　　　　

　　　　　　

などの式変形が理解できるのだという。これは、中学校で、

という図式を用いて、距離と時間と速さの関係を覚えさせている名残りのようだ。

　この図式は中学校では「ハジキの公式」として知られているが、「距離」を「道のり」、「速さ」
を「速度」と読み替えて、「ミソジの公式」とも言われるらしい。


平成１９年１２月１２日
　今日は、ぞろ目の日で縁起がいい。「イッチニー、イッチニー」と思わず声を掛けたくなる。
　数学の問題で、よく「小数部分」という言葉を耳にする。ところが、この言葉は、案外厳密
に教えられていないような気がする。

　たとえば、　「３．１４ の小数部分は？」と問われれば、間違いなく「０．１４」と答えられるだ
ろう。

　それでは、　「−３．１４ の小数部分は？」と問われれば、どう答えるのだろう？ここには、
多分世代間の差違が現れるに違いない。

　高校時代に、常用対数の問題で「指標と仮数」を学んだ世代は、多分、

　　　　　　−３．１４＝−３＋（−０．１４）＝−４＋（１−０．１４）＝−４＋０．８６

と計算して、小数部分は、「０．８６」と答えるだろう。

　最近の、常用対数が軽視されている世代では、多分迷うことなく、「−０．１４」と答えるだ
ろう。（こんなんで本当に大丈夫？）

　実数 ｘ に対して、ガウスの記号 ［ｘ］ は、ｘ を超えない最大の整数を表し、その値が、実
数 ｘ の整数部分と言われる。

　［ｘ］ ＝ ｎ　とおくと、　ｎ ≦ ｘ ＜ ｎ＋１　が成り立つ。

また、　ｄ ＝ ｘ − ｎ　とおくと、　０ ≦ ｄ ＜ １　が成り立ち、　ｘ ＝ ｎ ＋ ｄ　と書ける。

　この ｄ の値のことが、実数 ｘ の小数部分と言われる。

　したがって、「整数部分」、「小数部分」の定義に照らせば、

　　　［−３．１４］ ＝ −４　で、　ｄ ＝ −３．１４−（−４）＝４−３．１４＝０．８６

と求めるのが正解となる。

　ただ、大学入試問題を見る限りにおいて、負の数の小数部分を問う問題は出題されて
いないように思う。高校で、整数部分、小数部分の概念があまり教えられていないことを
配慮した上での、きっと老婆心なのだろう。

　例　円周率 π の小数部分は、　π−３　である。

　例　常用対数 ｌｏｇ₁₀２０００ の小数部分は、　ｌｏｇ₁₀２ である。

　例　 の小数部分は、　−１ である。

　例　− の小数部分は、　２− である。


平成１９年１２月３１日
　剰余の定理は、数学�Uで学ぶ。種々の計算の基本となる定理にも関わらず、以前と比
べて取り扱いが簡素化され、あまり深入りすることなく内容が薄くなっている。そのせいか、
整式の学習を終わった途端に記憶の彼方に消えてしまう生徒も多く、十分定着していない
というのが現状である。

　剰余の定理を用いて、余りを求めることは基本中の基本であるが、それで終わっては
「もったいない！」の一語に尽きる。

　若干骨のある問題を練習することにより、剰余の定理のよさを体験した方が定着率も
上がるというものだろう。

（教科書的な解法）　整式 Ｆ（ｘ） を （ｘ−１）（ｘ＋２） で割った商を Ｑ（ｘ）とすると、余りは

　　　　　　　　　　　　高々１次式で、　ａｘ＋ｂ　とおける。

　　　　　　　　　　すなわち、　Ｆ（ｘ） ＝ （ｘ−１）（ｘ＋２）Ｑ（ｘ）＋ａｘ＋ｂ

　　　　　　　　　　題意より、　Ｆ（１） ＝ ３　、　Ｆ（−２） ＝ −３　なので、

　　　　　　　　　　　　　　ａ＋ｂ＝３　、　−２ａ＋ｂ＝−３

　　　　　　　　　　この連立方程式を解いて、　ａ＝２　、　ｂ＝１

　　　　　　　　　　　よって、求める余りは、　２ｘ＋１　である。　（終）

（高校時代私が美しいと思った解法）　・・・・・　参考：「多項式の整除問題（１）」

　　題意より、　整式 Ｆ（ｘ） を ｘ−１ で割った商を Ｑ（ｘ）とすると、余りは、３ なので、

　　　　　　Ｆ（ｘ） ＝ （ｘ−１）Ｑ（ｘ）＋３

　と書ける。さらに、Ｑ（ｘ） を ｘ＋２ で割った商を Ｒ（ｘ）とすると、余りは、定数（ Ｃ ）なので、

　　　　　　Ｑ（ｘ） ＝ （ｘ＋２）Ｒ（ｘ）＋Ｃ

　と書ける。　よって、　Ｆ（ｘ） ＝ （ｘ−１）｛ （ｘ＋２）Ｒ（ｘ）＋Ｃ ｝＋３

　　　　　　　　　　　　　　　　　 ＝ （ｘ−１）（ｘ＋２）Ｒ（ｘ）＋Ｃ（ｘ−１）＋３

　　　Ｆ（−２） ＝ −３　なので、　　−３Ｃ＋３＝−３　　　ゆえに、　Ｃ＝２

　　よって、求める余りは、　２ｘ＋１　である。　（終）

　最近、河合塾の方からお話しを伺う機会があったが、河合塾では上記のような教え方は
しないそうである。「分かりにくい」という理由かららしい。

（河合塾における解答）

　　題意より、　整式 Ｆ（ｘ） を ｘ−１ で割った商を Ｑ（ｘ）とすると、余りは、３ なので、

　　　　　　Ｆ（ｘ） ＝ （ｘ−１）Ｑ（ｘ）＋３

　と書ける。　また、整式 Ｆ（ｘ） を ｘ＋２ で割った余りが、−３ なので、　Ｆ（−２）＝−３

　このとき、　　Ｆ（−２） ＝ （−３）Ｑ（−２）＋３ ＝ −３　　より、　Ｑ（−２） ＝ ２

　　よって、　Ｑ（ｘ） ＝ （ｘ＋２）Ｒ（ｘ）＋２　と書けるので、

　　　　　Ｆ（ｘ） ＝ （ｘ−１）｛ （ｘ＋２）Ｒ（ｘ）＋２ ｝＋３

　　　　　　　　 ＝ （ｘ−１）（ｘ＋２）Ｒ（ｘ）＋２（ｘ−１）＋３

　　　　　　　　 ＝ （ｘ−１）（ｘ＋２）Ｒ（ｘ）＋２ｘ＋１

　　よって、求める余りは、　２ｘ＋１　である。　（終）

（コメント）　非常に素朴な解法で、商 Ｑ（ｘ） を割るというアクロバット的な解法でない分、
　　　　　　分かりやすいんですかね？私はやはり商を割る方が好きかな．．．。


平成２０年２月１５日
　正弦定理は、余弦定理と並んで、「三角形を解く」ための有用な道具である。しかし、そ
の有用性にも関わらず、計算が思うように進まず誤った計算をする場合が非常に多い。

　一番多い誤りは、例えば、次のような計算をするときである。

　　　　　

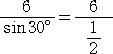
どうしても、生徒は「３」としがちである。何となくそうしたくなる気持ちは分かるが．．．。

　この場合は、
　　　　　　　　　　　

と計算するように指導しているのだが、なかなか定着しない！それが何となく疑問？


平成２０年２月２９日
　今日は、記念すべき閏年の「２月２９日」。１日得した気分で．．．。
　「数学�U」の定積分の学習も、面積計算をして締めくくられる。そこで、いつも思う疑問を
一つ。

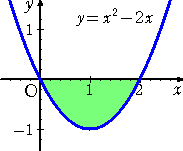　　　　左図の面積を求める場合、教科書では、

　　　　　　　　

　　　として解かれるが、積分記号の前の「−」が生徒にとっ
　　　ては悩める符号となっている。



　教科書では面積計算は全て天下り式なので、上記の公式をあえてあげる必要性はない
のではないだろうか？　面積計算はすべて、例えば、

　　　　　　　　　

のように差の形で求められる。この公式を活用すれば、上記の面積は、

　　　　　

として求められる。このような形で計算した方が計算ミスが少ないような気がするのだが、
教科書の執筆者はどのような考えで教科書を編集しているのだろうか？甚だ疑問だ。


平成２０年６月１３日
　「数学�V」では、「数学�U」で軽く扱われた極限が重厚に展開される。おそらく試験では、
どんな担当者も、次の問題を出したがる傾向にある。それは極限計算における「つまづき
チェック」になるからである。

　次の極限値を求めよ。
　　　　　　　　　　　　　　　

　この問題に対して、以前は次のように解かれていた（．．．と思う）。

　　

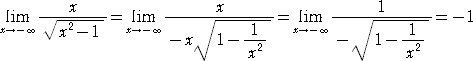
　しかし、この解法では、ｘ² を根号の前にくくり出すときに、「−ｘ」になるという急所が、「つ
まづきの元凶」となっていた。

　これに対して、最近は、　ｘ＝−ｔ　と置換して、

　　

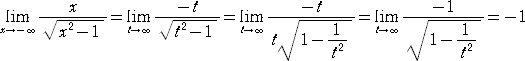
と指導される場合が多い。これだと、生徒は何も混乱なく正解に達する。

　でも、根号の性質の「機微」を避けているようで、私自身あまり好きになれない解法だ。


平成２０年１２月　５日
　このページの「三角比の覚え方」では、オーソドックスな覚え方を紹介したが、最近次の
ような覚え方も世間では流通しているらしい。

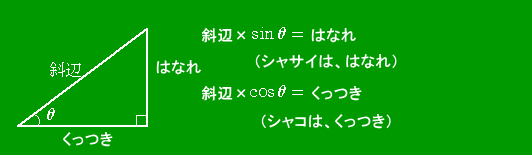　この覚え方だと、三角形が
　　　　　　　　

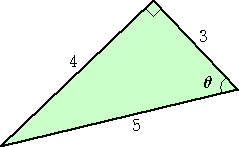
のようにトンデモナイ風になっていても正しく三角比が求められるかな？


平成２１年　１月２５日
　このページをご覧になった読者の方から、三角比の新しい覚え方をご教示いただいた。

　直角三角形を回転・反転して常に左下に角θがあるようにするという操作が必要だが、
「ウルトラマンのビームのポーズで．．．」と口添えれば、興味を持って覚えてくれるかもし
れない。
（あっ！でも、今の子って、「ウルトラマンのビームのポーズ」で通じるかな？ちょっと心配）

・　右肘部分は、常に直角 　・　左肘部分は、常に角θ 　・　左腕部分が、常に比の分母

　投稿されたＳさんによれば、「当時の同級生に教えたところ流行って、テストで手をパタ
パタする人が何人かいたのを覚えてる。」とのこと。


平成２１年　４月　１日
　今日から新しい年度が始まる。しかし、朝から関東地方は雨模様。この暗〜い天候の
中で、ふと疑問がわき起こった。

　疑問の対象は、次の数である。

　問題は、上記の数を「計算せよ。」ということだが、多分、出題者は、−（/２）ｉ　とする
ことを期待しているに違いない。ある方に伺うと、「分母を有理化せよ。」という言い方もあ
るらしいが、虚数単位を含む計算で、教科書等では、その表現は皆無である。

　「数の拡大」という視点に立てば、「分母の実数化」で、「−ｉ/」も○にしたいのだが、
どうであろうか？


平成２１年１１月３０日
　「過去の遺物」と言うと高校生が思わず頷いてしまう「対数」が未だに高校で教えられてい
るが、「対数」が持つ概念の重要性を考えれば当然だと思う。

　指数表現　ａ^ｘ＝Ｎ　と　対数表現　ｌｏｇ_ａＮ＝ｘ　は同値である。慣れてくると、どちらの表
現も自由自在と思うのだが、高校生の感覚からすると、

　対数表現　ｌｏｇ_ａＮ＝ｘ　から指数表現　ａ^ｘ＝Ｎ　を導くのに比べて

　指数表現　ａ^ｘ＝Ｎ　から対数表現　ｌｏｇ_ａＮ＝ｘ　を導くことに少し抵抗があるように感じる。

これは、どこから来る抵抗感なのだろうか？不思議な謎である。

　対数不等式　ｌｏｇ₂ｘ＜３　を解く問題で、教科書ではサラッと、「　０＜ｘ＜８　」としているが、

と補ってあげると合点する生徒が多い。

　多分、　「　３＝ｌｏｇ2□　」　より、　「□＝２³＝８　」　という計算感覚が、高校生の抵抗感
のない感覚と合致するからだろう。

　この感覚を利用して、対数関数　ｙ＝ｌｏｇ₂ｘ　のグラフを描くのに、指数関数　ｘ＝２^ｙ　のグ
ラフを活用する方がもしかしたら分かりやすいかもしれない。


平成２２年７月４日
　「０！＝１」だと約束してしまえばそれで済む話だが、その約束が納得されないと定着もし
ない。順列・組合せを学んでいる間は、「０！＝１」とすぐ答えられても、時期をずらして問い
かけると、ある自信（？）を持って、「０！＝０」と言い張る生徒が少なからずいる。

　２！＝２×１　と同様に考えて、０！＝０×１＝０　からくる誤った計算のためと思われるが、
この誤りを根絶することは難しい。

　教える側にとっても、「０！＝１」と説得するには準備が必要だ。私が高校生の頃、先生に
は次のように説明された。

　このように説明されて納得出来る生徒は、そもそも「０！＝１」であることに何ら疑問を持た
ない生徒だろう。

　問題は、自信（？）を持って、「０！＝０」と答える生徒をどう説得するかである。

　今までだと、「_ｎＰ_ｒ＝ｎ！/（ｎ−ｒ）！」の説明が煩わしいので、「約束だから．．．」と言い
張ってきたが、それではあまりにも対応が粗雑すぎる。

　また、Γ関数の性質　ｎ！＝Γ（ｎ＋１）　を用いて、

　　　　　　　　

と説明するのも大人げない。

　また、「ｎ！」は、ｎ個のものを並べる順列の数で、「０！」は「何も並べない場合」が１通り
あるから、「０！＝１」と考えるというのも何か騙されたようで胡散臭い。

　最近、「ａ⁰＝１」のときと同様の説得方法を考えることが出来た。

　この説明で納得されるかどうか少し不安であるが、「０！＝？」の質問があったときに試し
てみようと思う。

（追記）　この話題について、当ＨＰ読者のＨＮ「ＫＭ」さんからのコメントです。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成25年5月４日付け）
　0!=1 は集合論を用いて証明できますが、集合論を知らない人に 0!=1 となる理由を訊かれ
た場合は、「(n-1)!=n!/n に n=1 を代入する」で簡単に説明できると思います。


　当ＨＰ読者のＨＮ「Ｖ」さんからのコメントです。（平成25年5月４日付け）

　私は、0!=1は定義であって証明するものではないと認識していますが、何か証明法がある
のですか？


　ＫＭさんからのコメントです。（平成25年5月４日付け）

　0≦m≦n として Aをm個から成る有限集合、Bをn個から成る有限集合とするとき、AからB
への単射の総数は、 n(n-1)(n-2)...(n-m+1) になります。特に、m=n のときは全単射になり、
総数は n! になります。m=n=0 のときは全単射は空写像の1通りになります。よって 0!=1 で
す。


　当ＨＰがいつもお世話になっているＨＮ「らすかる」さんからのコメントです。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成25年5月４日付け）

　残念ながら、上記は、0!=1であることの証明になっていません。0!が未定義である前提に
おいては、「m=n のときは全単射になり、総数は n! 」になるのは、m=n≧1の場合だけです。
ここで、0!=1と定義すればうまくいきますので、0!=1と定義するというだけのことです。


　ＫＭさんからのコメントです。（平成25年5月４日付け）

　定理ではなく、「この場合、こう定義したほうが自然な感じがしてうまくいく」ということです
ね。ありがとうございました。


（コメント）　「この場合、こう定義したほうが自然な感じがしてうまくいく」ということではなく、
　　　　　　数学の諸概念に対して無矛盾であるように定義したと考えるべきでしょう。


　ＫＭさんからの情報です。（平成25年5月１０日付け）

　「0!=1、0⁰=1」についてのわかりやすい記事を見つけました。


（コメント）　上記の記事で、

　　　　　高校数学Aの教科書の２項定理の項目では、
　　　　　「ただし、 a^0＝1, b^0＝1 とする。」(a＝0 や b＝0 も除外していない！)

　　　　と述べていますが、私の記憶が確かであれば、教科書の冒頭に、「ａ は０とは異な
　　　　る」という類の注意書きがあると思うのですが．．．？


平成２２年１２月１日
　「負の数同士を掛けると正の数になる」は初学者にとっては一つの関門となる。次のよう
に考えれば、納得できるのではないだろうか？

　東西方向に数直線を置く。原点を境に左側が負の数、右側が正の数を表す。

ある人が、この数直線の道を西から東に向かって時速３ｋｍの速さで歩いている。ある時刻
に原点を通りすぎたとき、その２時間後、その人は原点より

　　　　　　　　３×２＝６（ｋｍ）

だけ東側の地点を歩いている。それでは、原点を通りすぎる２時間前、その人は

　　　　　　　　３×（−２）＝−６（ｋｍ）

だけ東側、すなわち、西側に６ｋｍの地点を歩いている。

　同様にして、ある人が、この数直線の道を東から西に向かって時速３ｋｍの速さで歩いて
いるときを考える。これを西から東に向かって時速−３ｋｍの速さで歩いていると考える。あ
る時刻に原点を通りすぎたとき、その２時間後、その人は原点より

　　　　　　　　（−３）×２＝−６（ｋｍ）

だけ東側の地点、すなわち、西側に６ｋｍの地点を歩いている。

　これは、東から西に時速３ｋｍで歩いている人が原点を通りすぎた後の２時間後にいる地
点としては妥当な結果である。

　それでは、原点を通りすぎる２時間前、その人は、　（−３）×（−２）（ｋｍ）だけ東側の地
点にいるわけだが、東側に６ｋｍの地点を歩いていることを考えると、

　　　　　　　　（−３）×（−２）＝６（ｋｍ）

とならざるを得ないわけである。納得できました？


　ＭＤＡさんに、もっと分かりやすい例示を頂きました。（平成２６年９月２９日付け）

　　前向きに3km/hで歩いているビデオを、

　　　1) 2時間再生すると   (+3) × (+2) ＝ +6
　　　2) 2時間逆再生すると (+3) × (-2) ＝ -6

　　後ろ歩きで3km/hで歩いているビデオを、
　　　3) 2時間再生すると   (-3) × (+2) ＝ -6
　　　4) 2時間逆再生すると (-3) × (-2) ＝ +6

　　実際に3分位のビデオを作って授業で見せたら、分かりやすそうですね。


（追記）　平成２８年１０月３０日付け

　「負×負＝正」の考え方に相通じるものとして、「÷Ａ/Ｂ＝×Ｂ/Ａ」がある。

　例えば、「１÷（１/３）」は、「１」の中に「１/３」がいくつあるかと考えれば、答えは「３」と直ち
に出るだろう。ここで、「１÷（１/３）」を、敢えて

　　１÷（１/３）＝１÷（１÷３）＝（１÷１）÷÷３＝１×３

と書くことにすれば、「÷÷＝×」という公式が誕生する。

（→　参考：「割り算の意味」）


　ｋｓさんからのコメントです。（平成２８年１１月１日付け）

　分配法則により、　(−１)×(−１)＋(−１)＝(−１)×（−１＋１）＝０　なので、

　　(−１)×(−１)＝１

　交換法則より、−Ａ＝−１×Ａとして、　(−Ａ)×（−Ｂ）＝ＡＢ


平成２５年５月１３日

　以下の話題は数学�V(平成２４年に高校入学)の内容です。弧度法は知っているものとしま
す。

　　複素数　＋ｉ　( ｉ は虚数単位) を極形式に直せ。


　結論から言えば、　＋ｉ ＝２{cos(π/6)＋ｉ・sin(π/6)}
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　※　ただし、偏角は、0 以上 2π 未満

ですが、これを教えるのは容易ではありません。自分でも教えるどころか解くだけでも悪戦
苦闘します。ましてや、大半の複素数は上記のような変形はできません。

　おそらく、＋ｉ は以下のような変形をされるでしょう。

　　＋ｉ ＝２(/2＋ｉ/2)＝２{cos(π/6)＋ｉ・sin(π/6)}

　自分が高校生のころはこのような内容はやっていませんが、先生方はどのような教え方を
されたのでしょうね。


（コメント）　複素数 ａ＋ｉ・ｂ に対して、ｘｙ座標系の平面上の点Ｐ（ａ，ｂ）を考える。座標軸の
　　　　　　原点をＯとして、

　　　　　　　　　ＯＰの長さを ｒ　、ｘ軸の正の向きから測ったＯＰのなす角を θ

　　　　　　とすると、　ａ＋ｉ・ｂ ＝ｒ（ｃｏｓθ＋ｉ・ｓｉｎθ）　と書ける。

　　　　　実際に、このように書けることは、右辺を計算して左辺になることを見せればよい。

　　　　　教科書等の導入の仕方（よおすけさんによるもの）に比べて、上記のように簡潔に
　　　　導入した方が生徒も受け入れやすく定着率もいいようです。多分、説明に５分！

　　　　　しばらくこの導入で慣れた後、よおすけさんによる解法を振り返ってみれば、多分
　　　　多くの生徒が合点するものと思われます。


平成２５年１０月１９日

　三角形の合同条件として、

（１）　対応する三辺の長さが等しい。（三辺相等）
（２）　対応する二辺の長さとその間の角が等しい。（二辺夾角）
（３）　対応する二角の大きさとその間の辺の長さが等しい。（二角夾辺）

がよく知られている。小学校５年で、図形の合同という概念を理解し、中学２年で合同条件
が触れられ、深化する。

　二つの図形は、次のそれぞれの場合に合同である。

（イ）　 一方の図形を移動して他方の図形に重ねることができる（合同の動的定義）
（ロ）　 二つの図形の対応する線分と対応する角がすべて等しい（合同の静的定義）

　学習指導要領では、

　・対応する３組の辺がそれぞれ等しい
　・対応する２組の辺がそれぞれ等しく、その間の角が等しい
　・対応する１組の辺が等しく、その両端の角がそれぞれ等しい

とあるので、教科書等もこの記載がされているものと思われる。ということは、現在の中学
校では、

　　三辺相等　、二辺夾角　、二角夾辺

などと簡略化した覚え方は教えられていないような．．．そんな雰囲気。「夾」という字が難し
いからだろうか？

　イギリスやアメリカなどでは、合同条件を

　　ＳＳＳ　、　ＳＡＳ　、　ＡＳＡ

と一口で覚える方法が用いられているそうだ。（ＳはＳｉｄｅ（辺）、ＡはＡｎｇｌｅ（角））

　概念を理解し使いこなすには、適切な覚え方が有効だと思うのだが、如何？


　当ＨＰがいつもお世話になっているＨＮ「ａｔ」さんからのコメントです。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２６年９月２７日付け）

　「ＳＳＳ、ＳＡＳ、ＡＳＡ」という覚え方は視覚的でしかも簡潔、覚えやすいですね。

　つい最近、[Angles of Intersecting Chords Theorem]と呼ばれているらしき定理を知りまし
た。（→　証明（動画））

　彼らが「the measure of the arc AB」 と呼んでいるものは、どうやら「弧ABに対する中心角
の大きさ」のことのようです。


平成２６年９月２６日

　比と言ったら、「ａ ： ｂ」のような書き方だし、比の値と言ったら、「ａ/ｂ」という書き方というの
は誰でも違和感なく受け入れられることだろう。

　ところが、「　ａ ： ｂ＝ａ/ｂ　」と書くと、途端に拒絶反応が．．．。何故だろう？

　そもそも、「ａ ： ｂ」というのは、ａはｂの何倍かを示すものなので、比の値そのものと混同し
てもよいと思う。

　相似比のように、比の値 ａ/ｂ を比ということもあるので特に大きな問題はないと思われる
が、若干の抵抗を感じる人は多い。比の値は、割合と同じ意味をもち、単位当たりの大きさ
と考えればよい。昔は、「：」と「÷」は同じ意味と教えられたものだが、最近ではどうも違うら
しい。

　私自身は、昔の教えに従って、「　ａ ： ｂ＝ａ ÷ ｂ＝ａ/ｂ　」と考える立場を堅持したいと思
う。

　日本では、除算記号としては、「÷」が使われるが、国によっては、除算記号として、「/」が
用いられ、インターネットの世界では除算記号は専ら「：」が用いられる。

　「/」は、英のオートレッドが使ったのが最初とされ、その歴史は「÷」よりも古いらしい。
　「：」は、独のライプニッツが使ったのが最初とされ、主にドイツで使われるらしい。


（追記）　ＨＮ「ＭＤＡ」さんより、上記の「意外な疑問」に対して意外な疑問をいただきました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２６年９月２６日付け）

　そうすると、13：12：5 = 13：2：30 = 13：60 となるのですか？


（コメント）　ｘ：ｙ：ｚ＝13：12：5　ということは、ｘ：ｙ＝13：12 かつ ｙ：ｚ＝12：5
　　　　　　である。従って、ｘ：ｙ＝13：12 を、ｘ：ｙ＝13：2 とすることはできない。


　らすかるさんからのコメントです。（平成２６年９月２６日付け）

　a：b=a÷b=a/b は、２値の比の場合だけ定義されるものであって、３値以上の比には適用
できないと思います。


（追記）　「比と比の値」と題して、ＨＮ「河下希」さんより、ご投稿いただきました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２９年３月１９日付け）

　「意外な疑問」の「比の記号」を読ませていただきました。

　２つの数の比というのは、２つの数の組を ａｄ＝ｂｃ となるようなときに、ａ：ｂ＝ｃ：ｄ とみな
した対象（大学レベルの言葉を惜しみなく使うなら、比とは、「Ｒ^２を、この同値関係で割った
商集合の元」）で、一つの実数である比の値 ａ/ｂ と比 ａ：ｂ は同じものではないと考えるの
が適当だと思います。

　２つの数の比の全体（実数の全体を数直線というのと同じような意味で）は射影直線と言
われますが、射影直線から１点∞を除いた集合と数直線との“自然な１対１対応”が、ａ：ｂ
を ａ/ｂ に直す操作といったところでしょうか。

　対応前のものと対応先のものを ａ：ｂ＝ａ/ｂ と等号で結んでしまうのは、f(x)=y を x=y と略
記するということなので、対応の仕方を一つ決めてしまうとしてもかなり違和感を覚えます。

＃　河下希さんのＨＰサイト「邪道数学研究所」


（コメント）　２値の比として、例えば、２：１、４：２、６：３、・・・　といろいろありますが、これらの
　　　　　　比の値は皆同じなので、

　　　　　　　　２/１＝４/２＝６/３＝・・・　　すなわち、　２：１＝４：２＝６：３＝・・・

　　　　　　集合 ｛ ２：１，４：２，６：３、・・・ ｝の代表元 ２：１ と比の値 ２/１ を同一視して、

　　　　　　　　２：１＝２/１

　　　　　　と見なすことはごく自然なことだと思うのですが．．．？


（追記）　上記話題について、ＨＮ「H．Nakao」さんより、メールでご投稿いただきました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（令和３年９月１９日付け）

　a：b を a/b と同一視する考え方にも一理あるのですが、b=0 のときの扱いや３項比 a：b：c
の扱いに多少の問題が発生します。

(1)　b=0 のときの比 a：b

　　日常的にも、比として、1：0 や 0：1 を使うことがありますが、a：b を a/b と同一視すると、
　0：1=0/1=0 は問題ないとしても、1：0=1/0　(割り算が定義できない)となり、a と b の役割
　が対等でなくなるので、困ってしまいます。

　0：0=0/0　(不定となる)は比として扱わないとすることには、異議はありません。

(2)　３項比 a：b：c の扱い

　　0 の扱いと ： の結合則が成立しない点から、a：b：c=(a：b)：c=(a/b)/c=a/(bc) と定義する
　のは、無理があると思います。

(3)　結論

　　(1)、(2)より、数学的には、a：b は、1次元の射影座標、a：b：c は、２次元の射影座標を
　表すと考えるのが自然です。

　　つまり、２項比 a：b は、以下のように定義できる。ここで、Rは実数体または有理数体ま
　たは複素数体とする。

　　集合R^2-{(0,0)}の2つの元 (a,b)、(c,d) に対して、関係〜を以下のように定義する。

　　 (a,b)〜(c,d)　<=定義=>　ある t∈R-{0} が存在して、(a,b)=t(c,d) である。

　関係〜が同値関係であることは、簡単に証明できる。

　２項比 a：b は、集合R^2-{(0,0)}を同値関係〜で割った同値類

　　a：b = {(x,y)∈R^2-{(0,0)} | (x,y)〜(a,b) }

と定義する。

　この定義の良いところは、aとbについて対等であること、簡単に高次元に拡張できること
です。

　例えば、３項比 a：b：c は、 集合R^3-{(0,0,0)}の同値関係〜による同値類とする。

ここで、関係〜は、集合R^3-{(0,0,0)}の同値関係

　　(a,b,c)〜(d,e,f)　<=定義=>　あるt∈R-{0}が存在して、(a,b,c)=t(d,e,f)である。

とする。

このとき、2：1 = 4：2 = 6：3 =・・・　、0：1 = 0：2 = 0：3 = ・・・　、1：0 = 2：0 = 3：0 = ・・・

　　　　　13：12：5 = 26：24：10 = 39：36：15 = ・・・　　となる。

(要約すると、ＨＮ「河下希」さんとほぼ同意見であるが、同値関係〜を定義する集合を、
R^2、R^3から、それぞれ(0,0)、(0,0,0)を除いたものとしているところが異なる。)


（コメント）　ＨＮ「H．Nakao」さん、コメントをいただき、ありがとうございます。


平成２６年１０月２日

　普段何気なく使っている言葉に「ｙ切片」というものがある。この言葉は直線の場合にしか
使わないと言う方もあり、放物線やいろいろな曲線がｙ軸と交わるときのｙ座標という意味で
使っている私としては肩身が狭い。高校の教科書等も「ｙ軸との交点」的な書き方で「ｙ切片」
という書き方にはなっていない。果たして、この「ｙ切片」という言い方は、どれくらいの認知度
があって、どの程度使っていいものか疑問になってきた。

　「切片」という言葉は、中学校で一次関数を教わるときに習って、その後、多様な関数を扱
うようになるころには、もう使わなくなってしまう言葉なので、１次関数専用と思われている方
がどうも多いらしい。