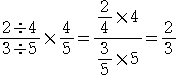・ 割り算の意味 S.H氏
割り算の問題で、例えば、「6÷3」は、次のように2通りの意味に解することができる。
(1) 等分除・・・全体量÷分割数=1分割当たり量
例 6個を3人に等分するとき、一人当たり2個となる。
(2) 包含除・・・全体量÷1分割当たり量=分割数
例 6個を一人当たり2個ずつ分けると、3人に分けられる。
「6÷3」の計算をするとき、上のどちらで計算しているのか、特に意識することはないと思
うが、
「6 の中に、3 が何個あるか?」 または 「3 に何を掛けたら、6
になるか?」
という認識は大切で、「2」という答を我々は得ることが出来る。
また、「3」を「1」と考えれば、「6」は「2」ということからも、「6÷3」の答が得られる。
(参考:私の疑問「Ⅱ」)
このような認識において、「1÷1/6」という割り算も、同様にできる。
この計算から、
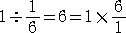
となり、分数で割ることは、その逆数を掛けることに等しいことが分かる。
「分数で割ることは、その逆数を掛けることに等しい」ということに関して、次のような説明
もあることを最近知った。
「6÷3」は、「3 に何を掛けたら、6 になるか?」という認識を活用したものである。
いま、試しに次のような計算をしてみる。
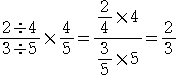 |
が成り立つ。これは、 |
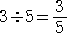 |
ということを用いてい |
るが、「示すべき事柄を用いている」という不安があるので、
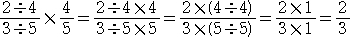
と式変形して求めてもよい。したがって、このとき、
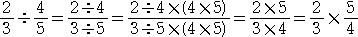
が成り立つ。
(参考文献:木村俊一 著 算数の究極奥義教えます(講談社))
(追記) 部屋で仕事をしていたら、ふらっと事務のHさんが現れて、私の疑問を解決してほ
しいと頼まれた。それは、「分数で割るとき、逆数に直して掛けるのはなぜか?」と
いうものだった。(H16年8月11日付け)
このページを引き合いに出して説明を始めたのだが、いざ読み返してみると、「ず
いぶん分かりにくいな!」ということに気づかされた。
Hさんも納得いかないようで困っておられた。そこで、次のように説明してみた。
6÷1=6 のように、1 で割る場合、その答はたちどころに出る。
そこで、6÷2 で、割る数 2 を 1 にすることを考えればよい。
2 を 1 に、すなわち半分にすれば、6 も半分になって、3 。これが答になる。
したがって、
A÷B の計算は、C÷1(1当たりの量の計算)の C を求めることに等しい。
ところで、
|
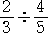 |
の計算で、割る数 |
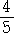 |
を 1 にするには、 |
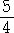 |
を掛ければよい。 |
よって、
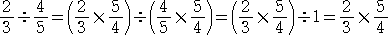
このことから、分数で割るときは、逆数に直して掛ければよい。
このように説明してみたら、Hさん、「今日の説明で、一番分かった!」と合点して帰
られた。
(追記) 平成24年12月9日付け
塾生たちの様子を見ていると、 「÷分数」はひっくり返して掛ける ということを、理由も
考えず、単なる計算規則として覚えているにすぎないような雰囲気。
問題 8/3m2の畑に、水9/4リットルの水を均等にまくとき、1m2あたり何リットルまかれ
たことになるか?
上記の説明の通り計算すれば、次のようになるだろう。
9/4÷8/3の計算で割る数8/3を1にするには、3/8を掛ければよいから、
答は、9/4×3/8=27/32(リットル)となる。
計算だけだと無味乾燥なので、次のような図を活用すればもっと分かりやすくなるかな?
底面積8/3m2の水槽に水を9/4リットル入れるものと考え、水槽を真横から眺める。
(水槽の底面は、1m×8/3mの長方形とする。)
|
水を9/4リットル
↓ |
割り算の答は、1m2の上に水がどれだけある
かを見いだすことに等しい。
|
| |
|
|
底面積8/3m2 |
水槽に、辺の長さが8/3mの方を横に1/3毎、高さは縦に1/4毎に区切り線を入れる。
|
水を9/4リットル
↓ |
|
| |
|
← 9×8=72個の直方体に分割
1リットルはちょうど 4×8=32個の直方体を
集めたもの。 |
|
底面積8/3m2 |
|
底面1m2の上に直方体が 9×3=27個ある。よって、求める答は、 27/32 となる。
(コメント) 9/4÷8/3の計算が、(9×3)/(4×8) すなわち、 9/4×3/8 ということが
視覚的に理解されるかな?
(追記) 平成25年10月12日付け
江藤邦彦 著 「お父さんのための数学 100の常識 (日本実業出版社)
を読んでいて、次の問いにハッとさせられた。
3÷5 は何故 3/5 に等しいか?
この問いかけをされて、「そんなの当たり前じゃん」とか「そういう決まりだから」と答える人
の何と多いことか...。実は、正直に告白すると、私もその一人。特に何も考えずに、今ま
で「3÷5=3/5」としてきた。これにも説明が必要とは正直驚いた。
次のように説明するといいらしい。
3本のカステラがあります。これを5人で等分するという計算が「3÷5」で、その計算結果が
一人の取り分になります。
ところで、1本のカステラを5等分すると、一人当たりの取り分は、1/5。カステラが3本ある
ので、一人の取り分は、 1/5+1/5+1/5=3/5 となります。
以上から、 3÷5=3/5 と言えます。
(コメント) 分かったような分からないような、そんな...雰囲気!「1÷5」を「1/5」と決めつ
けている時点で話は終わりかな?