
丂桳棟悢慡懱 俻 偼懱乮懄偪丄巐懃墘嶼偑壜擻側廤崌乯偱偁傞丅俀偮偺桳棟悢 倎丄倐 偵懳偟偰丄
丂丂丂丂丂丂丂丂倎亄倐丒倝丂乮倝 偼丄嫊悢扨埵乯
偺慡懱傕懱偲側傞丅偙傟偼丄俻乮倝乯 偲昞偝傟傞丅乮仺嶲峫丗惍悢榑偺婎慴抦幆乯
丂崅峑偺嫵壢彂乮悢妛俬俬乯偺栤戣偵丄
桳尷奼戝懱偺惈幙 丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂桳棟悢慡懱 俻 偼懱乮懄偪丄巐懃墘嶼偑壜擻側廤崌乯偱偁傞丅俀偮偺桳棟悢 倎丄倐 偵懳偟偰丄
丂丂丂丂丂丂丂丂倎亄倐丒倝丂乮倝 偼丄嫊悢扨埵乯
偺慡懱傕懱偲側傞丅偙傟偼丄俻乮倝乯 偲昞偝傟傞丅乮仺嶲峫丗惍悢榑偺婎慴抦幆乯
丂崅峑偺嫵壢彂乮悢妛俬俬乯偺栤戣偵丄
| 丂丂丂丂丂丂 |
丂傪寁嶼偣傛丅 |
偲偄偆傕偺偑偁傞丅偙傟偼丄暘曣偺幚悢壔傪懀偡栤戣偱丄
丂丂丂丂丂丂丂![]()
偲側傞丅
丂拞妛峑偱丄暘曣偵柍棟悢偑偁傞応崌偵偼暘曣偺桳棟壔傪峴偆偲偄偆寁嶼偑偁傞偑丄偙傟
偼丄悢偺偍偍傛偦偺抣傪攃埇偡傞偨傔偺寁嶼偱偁偭偨丅乮仺嶲峫丗庤寁嶼偑柺敀偄乯
丂偦傟偱偼丄暘曣偺幚悢壔偵偼偳傫側堄枴偑塀偝傟偰偄傞偺偐丄崱傑偱偼偭偒傝偲帺妎偡傞
偙偲偼側偐偭偨丅乮扨側傞寁嶼栤戣偲巚偭偰偄偨両乯
丂偙偺揰偵娭偟偰丄摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵僴儞僪儖僱乕儉乽倀乿偝傫偲偄偆曽偑堄梸
揑偵寈忇傪側傜偟偮偮搳峞偝傟偨丅宖帵斅偺彂偒崬傒偼帪娫偲偲傕偵徚偊嫀偭偰偟傑偆塣柦
側偺偱丄倀偝傫偺尋媶寢壥傪婰榐偲偟偰巆偡傋偔丄偦偟偰丄巹偺棟夝傪怺傔傞偨傔偵丄偙偺儁
乕僕傪婲偙偡偙偲偵偟偨丅
丂丂丂丂丂丂丂![]()
偺寁嶼偱摿昅偡傋偒偙偲偼丄嵍曈偑偳傫側暘悢偱偁傟丄昁偢
丂丂丂丂丂丂丂丂倎亄倐丒倝丂乮倝 偼丄嫊悢扨埵乯
偺宍偵昞偝傟傞偲偄偆揰偱偁傞丅偙偺偙偲偼丄嫊悢扨埵 倝 傪娷傓暘悢偼寢壥揑偵懚嵼堄媊
偼側偔丄壛朄丒尭朄丒忔朄偺傒偑墘嶼偲偟偰嫋偝傟傞廤崌乮娐偲偄傢傟傞両乯
俻[倝] 偲幚幙揑偵
摨偠偩偲偄偆偙偲偱偁傞丅
丂偟偨偑偭偰丄暘曣偺幚悢壔偲偄偆寁嶼偺恀幚偺堄枴偼丄
丂丂丂丂丂丂丂俻乮倝乯亖俻[倝]
偲偄偆晽偵側傞偺偩傠偆丅
丂偮傑傝丄丂俻乮倝乯 偼丄乷 侾丆倝 乸傪婎掙偲偡傞俻忋偺俀師尦儀僋僩儖嬻娫偱偁傞偲偄偊傞丅
偙偺偲偒丄俻乮倝乯 偼丄桳棟悢懱 俻 偺俀師奼戝懱乮俀師懱乯偲偄傢傟傞丅
丂俲 傪懱 倠 偺奼戝懱偲偟丄兛 傪 俲 偺尦偲偡傞丅
丂丂丂倎 亄 倐兛 亄 們兛2 亄 丒丒丒 亄 倓兛値 丂乮倎丄倐丄們丄丒丒丒丄倓 偼 倠 偺尦乯
偺廤崌偼丄 倠 傪娷傓俲偺晹暘娐偱丄兛 傪娷傓傕偺偺拞偱嵟彫偺傕偺偱偁傞丅
丂偙偺廤崌偼丄倠[兛] 偲彂偐傟傞丅
丂倠[兛] 偑丄倠 忋桳尷師尦偱偁傞偲偒丄兛 偼丄倠 忋戙悢揑側尦偲偄偆丅
偟偨偑偭偰丄俲 偑懱 倠 偺桳尷奼戝懱偺偲偒丄俲 偺尦偼慡偰丄倠 忋戙悢揑偲側傞丅
丂偙偺偙偲偐傜丄俻乮倝乯 偺尦偼慡偰丄俻忋戙悢揑偲側傞丅
偮傑傝丄昁偢丄倎亄倐丒倝丂乮倝 偼丄嫊悢扨埵乯偺宍偵昞偝傟傞偲偄偆傢偗偩丅
椺丂俻忋婛栺側懡崁幃 倶3亅俀倶亅俀 偵偍偄偰丄倶3亅俀倶亅俀 亖侽丂偺崻傪 兛 偲偡傞丅
丂丂偙偺偲偒丄丂兛/乮侾亄兛乯丂傪丄兛 偺惍幃偲偟偰昞偣丅
乮夝乯丂兛 偼丄俻忋戙悢揑側尦側偺偱丄俻乮兛乯亖俻乵兛乶 偑惉傝棫偮丅
丂丂丂俻乵兛乶 偼丄乷 侾丆兛丆兛2 乸傪婎掙偲偡傞俻忋偺俁師尦儀僋僩儖嬻娫偱偁傞丅
丂丂丂傛偭偰丄丂兛/乮侾亄兛乯亖俙亄俛兛亄俠兛2丂偲彂偗傞丅
丂丂丂暘曣傪暐偭偰惍棟偡傞偲丄
丂丂丂丂丂丂兛亖俙亄乮俙亄俛乯兛亄乮俛亄俠乯兛2亄俠兛3
丂丂丂丂兛3亖俀亄俀兛丂側偺偱丄
丂丂丂丂丂丂俙亄俀俠亄乮俙亄俛亄俀俠亅侾乯兛亄乮俛亄俠乯兛2亖侽
丂丂丂乷 侾丆兛丆兛2 乸偼丄侾師撈棫側偺偱丄
丂丂丂丂丂丂俙亄俀俠亖侽丂丄丂俙亄俛亄俀俠亅侾亖侽丂丄丂俛亄俠亖侽
丂丂丂偙傟傪夝偄偰丄丂俙亖俀丂丄丂俛亖侾丂丄丂俠亖亅侾
丂丂丂傛偭偰丄丂丂兛/乮侾亄兛乯亖俀亄兛亅兛2丂乮廔乯
楙廗栤戣丂丒丒丒丂倀偝傫偑弌戣偝傟偨栤戣偱偡丅
丂俻忋婛栺側懡崁幃 倶3亅俀倶亅俀 偵偍偄偰丄倶3亅俀倶亅俀 亖侽丂偺崻傪 兛 偲偡傞丅
師偺幃傪兛 偺惍幃偲偟偰昞偣丅
乮侾乯丂乮俆俆亄兛亄俀兛2亄俁兛3亄係兛4亄俆兛5亄俇兛6亄俈兛7乯
丂丂丂/乮侾俋係亄兛亄俉兛2亄俀俈兛3亄俇係兛4亄侾俀俆兛5乯
乮俀乯丂乮侾俋係亄係兛亄侾俇兛2亄俁俀兛3亄係係兛4亄俆俀兛5亄俇侽兛6亄俇俋兛7亄係俇兛8
丂丂丂丂亅侾俁兛9亅係俉兛10亅俀俁兛11亄俇兛12亄俈兛13乯
丂丂丂/乮侾侾俈亅俀兛亅俀俆俉兛2亅係俇俁侽兛3亅俁俈侾係侾兛4
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亅侾俉俉俉俋侽兛5亅侾俆係侽俇俁兛6亄侾俇俁俉係兛7亄俈俉侾俀俆兛8乯
丂夝摎偼丄撉幰偺曽偵偍傑偐偣偟傛偆丅夝摎偝傟偨曽丄偙偪傜傑偱儊乕儖偱偛嫵帵偔偩偝偄丅
丂丂丂丂嬻廙偝傫偑忋婰偺楙廗栤戣偵庢傝慻傑傟偨丅乮暯惉俀俁擭侾俀寧俀俇擔晅偗乯
丂丂丂丂(1)丂偲傝偁偊偢丄暘巕丄暘曣偦傟偧傟忚梋傪偲偭偰丄師悢傪壓偘傑偡丅偦偺寢壥丄暘
丂丂丂丂丂丂巕丄暘曣偼丄偦傟偧傟師偺傛偆側俀師幃偵側傝傑偟偨丅
丂丂丂丂丂丂丂丂(100兛2+167兛+161)/(386兛2+683兛+748)
丂丂丂丂丂丂暘曣偺媡尦傪媮傔偰丄暘巕偲偐偗偨傕偺偑摎偊偵側傞偼偢偱偡丅
丂丂丂丂丂悢帤偑偁傑傝偵傕戝偒偄偺偱丄傓偟傠堦斒壔偟偰丄倶2+倫倶+倯 偺媡尦傪寁嶼偟傑偟偨丅
丂丂丂丂丂丂(倶2+倫倶+倯)X-(倶3+倎倶+倐)Y=Z丂偲偍偄偰丄晛捠偺忚梋娐偺媡尦傪媮傔傞傛偆偵寁嶼丅
丂丂丂丂丂偦偺寢壥丄媡尦 X/Z = {1/(倯-倫俻+俻2)}{1+ (倶2-俻倶+俻倫-倫2)/(倫2-倯-2)} 傪摼傑偟偨丅
丂丂丂丂丂偙偙偱丄(倫倯-2)/(倫2-倯-2)=Q 偲偍偒傑偟偨丅
丂丂丂丂丂屻偼丄倫=683/386丄 倯=748/386 傪戙擖偟偰丄暘巕偲偐偗偰揥奐偟偰丄偦傟偐傜
丂丂丂丂丂倶3-2倶-2 偺忚梋傪偲偭偰丄暘曣偺386傪朰傟偢崌傢偣偰廔椆偱偡丅
丂丂丂丂丂丂(465235兛2+581738兛+5479146)/31932564
丂丂丂丂丂偲側傝傑偟偨丅
丂丂丂(2)丂偦傟偧傟忚梋傪偲偭偰師悢傪壓偘偰偄偔偲戝偒側學悢偼偩傫偩傫彫偝偔側傝丄寢嬊
丂丂丂丂丂掕悢偟偐巆傝傑偣傫偱偟偨丅偦傟偱摎偊偼丄
丂丂丂丂丂丂丂117/194
丂丂丂丂丂偲偄偆偙偲偵側傝傑偟偨丅乮寁嶼偱偼Maxima傪嬱巊偟傑偟偨乯
丂丂丂偙偙偱丄幚梡揑側帠暱偲偟偰丄
丂丂丂丂懡崁幃 倫(倶)丄倯(倶) 偵偮偄偰丄倫(倶)=0 偲 倯(倶)=0 偑嫟捠夝傪傕偨側偄偲偒丄
丂丂丂丂丂倎(倶)倫(倶)+倐(倶)倯(倶)=1 偲側傞懡崁幃 倎(倶)丄倐(倶) 傪摼傞偙偲偑偱偒傞丅
丂丂丂偙傟偑丄惍悢偺応崌偲摨條偵惉傝棫偮傛偆偱偡丅偦傟偱丄嬶懱揑偵愭偺傛偆側媡尦傪媮
丂丂傔傞偙偲偑偱偒傑偟偨丅
丂丂乮僐儊儞僩乯丂嬻廙偝傫丄夝摎傪偁傝偑偲偆偛偞偄傑偡丅學悢偺戝偒偝偵埑搢偝傟傑偡両
丂丂丂丂俽乮俫乯偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭侾寧俁侾擔晅偗乯
丂丂丂丂丂楙廗栤戣偵嬻廙偝傫偑庢傝慻傑傟偰偍傜傟偨偺偱丄暿偺帇嵗偐傜捛帋偟偨偲偙傠丄
丂丂丂丂丂乮悽奅堦抁偄掕棟丗Q(兛)=Q[兛] 偺傒傪巊偄傑偡丅乯
丂丂丂丂丂丂丂乮俆俆亄兛亄俀兛2亄俁兛3亄係兛4亄俆兛5亄俇兛6亄俈兛7乯
丂丂丂丂丂丂丂丂丂丂/乮侾俋係亄兛亄俉兛2亄俀俈兛3亄俇係兛4亄侾俀俆兛5乯
丂丂丂丂丂丂偑嵍曈偺尦丄偟偨偑偭偰丄倎兛2 + 倐兛 + c丂偲堦堄揑偵昞尰偝傟傞両側傞帇嵗偱丄
丂丂丂丂丂丂暘曣傪偼傜偄惍棟偟丄
丂丂丂丂丂丂丂丂161 - 1366倎 - 772倐 - 748們 + (167 - 2138倎
- 1520倐 - 683們)兛
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 +
(100 - 1520倎 - 683倐 - 386們)兛2
丂丂丂丂丂丂Q忋俁師偺奼戝懱乮偱丄1丄兛丄兛2 偑Q忋慄宆撈棫傪偮偐偆偲師傪夝偗偽傛偄乯
丂丂丂丂丂丂丂{161 - 1366*a - 772*b - 748*c=0, 167 - 2138*a - 1520*b - 683*c=0
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂, 100 - 1520*a
- 683*b - 386*c=0}
丂丂丂丂丂丂傪乽Wolfram|Alpha乿偵憓擖偟丄夝傪丄倎兛2 + 倐兛 + c丂偵戙擖偟摎偊丅
丂丂丂丂丂丂乽寁嶼偱偼Maxima傪嬱巊偟傑偟偨乿偲嬻廙偝傫丅Maxima 偑儈僗傪偟偨偺偐傕偟傟傑
丂丂丂丂丂丂偣傫丅乮搑拞偑暁偣偰偁傞偺偱傢偐傝傑偣傫偑丏丏丏丅)
丂丂丂丂丂丂丂偲偙傠偱丄傕偆堦栤丗
丂丂丂丂丂丂丂乮俆俆亄兛亄俀兛2亄俁兛3亄係兛4亄俆兛5亄俇兛6亄俈兛7乯
丂丂丂丂丂丂丂丂丂丂/乮侾俋係亄兛亄俉兛2亄俀俈兛3亄俇係兛4亄侾俀俆兛5乯
丂丂丂丂丂丂傪夝偲偡傞俁師曽掱幃傪憂嶌偟丄F[X]=0 偺夝傪兝偲偡傞偲偒丄懠偺夝偑(伕Q[兝]
丂丂丂丂丂丂偱側偄偙偲偵棷堄 )
丂丂丂丂丂丂丂冃[兝]=-((116276074206*I*兝^2)/(1536062201*Sqrt[19])) +
丂丂丂丂丂丂丂丂丂丂((-18588975415993129437314259380413 +
丂丂丂丂丂丂丂丂21*I*Sqrt[197970509704538237555447469669863821432657096\
丂丂丂丂丂丂丂丂丂丂丂893991368108534019])*兝)/37177950831986258874628518760826
+
丂丂丂丂丂丂丂丂丂丂(453943487050089557 - 304165603040508613*I*Sqrt[19])/
丂丂丂丂丂丂丂丂丂丂丂1494870061805634687
丂丂丂丂丂丂偲側傝丄偁偲傂偲偮偼丄冃[冃[兝]]偱偁傞偙偲傪帺柧偱傕帵偟偰偔偩偝偄丅
丂丂丂丂丂丂崱夞偺偼丄乽旝暘僈儘傾棟榑乿偺椺偲堘偄偑暘偐傞堊偺栤戣採婲偱偡丅
丂丂丂丂丂丂忋偼丄斞崅愭惗偑僈儘傾棟榑偺島媊偱丄攡懞丂峗丂懡尦悢棟壢妛愱峌嫵庼巵偑
丂丂丂丂丂丂樧忋偵嵹偣偰偍傜傟傞僥乕儅偵傕捈偖暻偵傇偪偁偨傝崲擄偵棫偪岦偐偆摫擖椺偲
丂丂丂丂丂丂偟偰傛偄偺偱丄嵟弶偵泏惗偵栤傢傟偨栤偱偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭侾寧俁侾擔晅偗乯
丂屳彍朄偺寁嶼偱偼丄Maxima 偱妋擣偟偮偮丄妱偲庤寁嶼儀乕僗偱峴偄傑偟偨丅乮偪傚偭偲妋
擣偡傞偲丄屳彍朄偺寁嶼偑娫堘偭偰偄傞傛偆偵尒偊傑偟偨乯庤寁嶼偺儊儌偑傕偆側偄偺偱丄偳
偆娫堘偊偨偐挷傋傞偙偲偼偁偒傜傔偰丄崱屻偙傫側栤戣偱偼丄屳彍朄傛傝傕楢棫曽掱幃傪巊
偆曽朄傪専摙偟傑偡丏丏丏両
丂偲偙傠偱丄乽傕夝乿偺榖戣偵偮偄偰偼埲慜傛傝婥偵側偭偰偄傑偟偨丅崱偺強丄弰夞娭悢偼俁師
偱偼岞幃揑偵摼傜傟傞偑丄堦斒偵偼梕堈偵摼傜傟偢丄弰夞娭悢偑暘偐偭偰偄傞幃傪偄偠偔偭
偰暿偺幃偺弰夞娭悢傪摼傞丄偁傞偄偼丄岺晇偟偰弰夞娭悢偑暘偐傞傛偆側幃傪峔惉偡傞側偳
偺傛偆側悽奅側偺偱偼側偄偐偲棟夝偟偰偄傑偡丅
丂偝偰丄乮學悢偑傛傝偐傢偄偄乯栤戣偑乽夝偺弰夞乿偵偁傝傑偟偨偺偱丄偦偪傜傪峫嶡偟傑偟偨丅
丂俁師曽掱幃丂倶3亅俁倶亄侾亖侽丂偺夝傪 兛
偲偡傞偲偒丄師偺栤偄偵摎偊傛丅
丂丂乮侾乯丂乮俁兛2亄俆兛亄俈乯/兛丂偺嵟彫懡崁幃丂倫乮倶乯丂傪媮傔傛丅
丂倖乮倶乯亖倶3亅俁倶亄侾丂偺夝兛偵懳偟偰丄 倗(兛)亖乮俁兛2亄俆兛亄俈乯/兛 傪夝偲偡傞曽掱幃偼丄
resultant(倖(倗(倶)亅倷亄倶)丆倖(倶)丆倶) 偵尰傟傞偙偲傪棙梡偡傞丅
丂偙傟傪寁嶼偡傞偲丄俁師幃偺場悢偑暋悢偁傞偺偱丄偳傟偐傪敾暿偡傞偨傔偵丄
resultant(倖(倷亅倗(倶)亄倶)丆倖(倶)丆倶) 偵傕尰傟傞偙偲傪棙梡偡傞丅嫟捠偟偰懚嵼偡傞場悢偼丄侾偮
偟偐側偐偭偨偺偱丄偦傟偑丄偡側傢偪丄丂倫(倷)亖倷3亅俁俇倷2亄侾俋俆倷亄侾俇侾俋丂偲摼傞丅
丂倫乮倶乯亖侽丂偺夝傪丄兛1丄兛2丄兛3丂偲偡傞偲偒丄
丂丂乮俀乯丂兛2
傪丄兛1 偺俀師幃 俥(兛1)
偱昞偣丅
丂倷亖倗(倶)亖俁倶亄俆亄俈/倶亖亅俈倶2亄俁倶亄俀俇
[俈/倶亖俈(亅倶3亄俁倶)/倶丂偺惍棟傪埫嶼偱傗偭偨傜丄俀夞傕娫堘偊傑偟偨丏丏丏]
丂倎倷2亄倐倷亄們亖倶 偲側傞 倎丄倐丄們 偑傎偟偄丅丂倷2亖丒丒丒亅俀侽俉倶2亅侾俋倶亄俈侾俉丂傛傝
丂亅俀侽俉倎亅俈倐亖侽丂丄亅侾俋倎亄俁倐亖侾丂丄俈侾俉倎亄俀俇倐亄們亖侽
偙傟傪夝偐偣傞偲丄丂倎亖亅俈/俈俆俈丂丄丂倐亖俀侽俉/俈俆俈丂丄丂們亖亅俁俉俀/俈俆俈
丂f(倶) 偺弰夞娭悢 倶2亅俀 傪棙梡偟偰丄
丂F(倷)亖g(倶2亅俀)亖亅俈(倶2亅俀)2亄俁(倶2亅俀)亄俀俇
丂丂丂丂丂丂丂丂丂丂亖丒丒丒
丂丂丂丂丂丂丂丂丂丂亖侾侽倶2亄俈倶亅俉亖侾侽(倷亅俁倶亅俀俇)/俈亄俈倶亅俉
丂偙傟偵丄丂倶亖倎倷2亄倐倷亄們丂偲忋婰 倎丄倐丄們 傪戙擖偝偣傞偲丄
丂丂丂F(倷)亖亅(侾俋倷2亅侾俇係俇倷亄俁俆俀侾侽)/俈俆俈
丂丂乮俁乯丂兛2 傪丄兛1 偺侾師暘悢幃 俧乮兛1乯 偱昞偣丅
丂(倷亄倎)(俁俈倷2亅侾俆俁俀倷亄侾侽俀俁俉) 偑侾師幃偲側傞傛偆偵丏丏丏丂倎亖俀侽侽/俁俈
偦偆偄偆傢偗偱丄F(倷)偺暘曣暘巕偵丄俁俈倷亄俀侽侽傪妡偗偝偣偰丄
丂G(倷)亖俈俆俈(俀俆俈倷亄俀俀俁)/乷俈俆俈(俁俈倷亄俀侽侽)乸亖(俀俆俈倷亄俀俀俁)/(俁俈倷亄俀侽侽)
丂(偙偙偱栺暘偱偒傞偙偲偼晛曊側偺偩傠偆偐丏丏丏丠)
丂丂乮係乯丂俻乵倶乶/乮倫乮倶乯俻乵倶乶乯丂偼懱偱偁傞偙偲傪帵偣丅
丂擟堄偺尦 A(倶)亗0 偵偮偄偰丄媡尦偺懚嵼傪妋偐傔傞丅
丂倫(倶)偼婛栺側偺偱丄[婛栺側俁師幃 f(倶)亖侽 偺夝兛偺俀師幃偨偪偑夝偩偐傜]
A(倶)偲倫(倶)偼嫟捠場悢傪帩偨側偄丅傛偭偰丄屳彍朄偵傛偭偰丄A(倶)B(倶)亄倫(倶)C(倶)亖侾
傪峔惉
偱偒傞丅B(倶)偑A(倶)偺媡尦偲側傞丅懠偺梫審偼偨傇傫帺柧偲巚偆丅
丂丂乮俆乯丂俻乵倶乶偵偍偄偰丄乮倫乮倶乯俻乵倶乶乯
偼嬌戝僀僨傾儖偱偁傞偙偲傪帵偣丅
丂乮倫乮倶乯俻乵倶乶乯 埲奜偺壗偐傪娷傓僀僨傾儖俼偑偁偭偨偲偡傞偲丄偦偺壗偐A(倶)偼丄倫(倶)偱妱
偭偨忚梋偑亗0偱偁傞偐傜丄忋婰偺B(倶)傪妡偗傞偙偲偱丄A(倶)B(倶)亖亅倫(倶)C(倶)亄侾伕俼丂偲側
傝丄偡側傢偪丄侾伕俼 偱偁傞偐傜丄俼偼Q[倶]帺懱偲側偭偰偟傑偆丅傛偭偰丄乮倫乮倶乯俻乵倶乶乯
偼嬌戝
僀僨傾儖偱偁傞丅
丂丂乮俇乯丂倫乮倶乯亖侽
偺敾暿幃俢傪媮傔傛丅
丂倖乮倶乯亖倶3亅俁倶亄侾丂偺夝傪 倶1丄倶2丄倶3丄 倫(倷)偺夝傪 倷1丄倷2丄倷3 偲偐偔丅
丂倖乮倶乯亖侽丂偺敾暿幃 D'亖81(僇儞僯儞僌偵傛傞丅)偼婛抦偲偡傞曽恓偱丄
丂丂D亖{(倷1亅倷2)(倷3亅倷2)(倷1亅倷3)}2亖{(g(倶1)亅g(倶2))(g(倶3)亅g(倶2))(g(倶1)亅g(倶3))}2
丂丂 亖{(亅俈(倶1亄倶2)亄俁)(倶1亅倶2)丒丒丒}2
丂丂 亖[亅俈3(倶1亄倶2)(倶2亄倶3)(倶3亄倶1)亄俈2丒3{(倶1亄倶2)(倶2亄倶3)亄丒丒丒}
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亅俈丒俁2{(倶1亄倶2)亄丒丒丒}亄俁3]2丒D'
丂丂丂(倶1亄倶2)(倶2亄倶3)(倶3亄倶1)亖(倶1亄倶2亄倶3)(倶1倶2亄倶2倶3亄倶3倶1)亅倶1倶2倶3亖侾
丂丂丂(倶1亄倶2)(倶2亄倶3)亄丒丒丒亖(倶1亄倶2亄倶3)2亄(倶1倶2亄倶2倶3亄倶3倶1)亖亅俁
丂丂丂(倶1亄倶2)亄丒丒丒亖俀(倶1亄倶2亄倶3)亖侽 摍偵傛偭偰丄
丂丂D=(亅俈3亄俈2丒俁丒(亅俁)亄俁3)2丒俉侾亖(亅俈俆俈)2丒俉侾亖係俇係侾俇俋俇俋
丂丂乮偙偙偱丄僐儞僺儏乕僞偑 倫(倷)偐傜媮傔傞抣偲堦抳偟側偐偭偨偺偱丄偙偙偵偒偰丄(俀)偺寁嶼
丂丂丂娫堘偄[掶惓嵪]偑敪妎偟偨傢偗偱偡丅乯
丂丂乮俈乯丂傛傝崅師偺曽掱幃偱丄乮俀乯偺傛偆側弰夞孮 G 偑嶌梡偟丄夝偺婳摴
G乮兛1乯
丂丂丂丂偑慡偰傪恠偔偡傛偆側嬶懱椺傪偁偘丄偦傟傜傪徹柧偣傛丅
丂埲慜偺峫嶡傪棳梡偟偰丄曽掱幃 倶4亄俆倶3亄俆倶2亅俆倶亅俆亖侽 偵偮偄偰丄f(倶)亖亅倶2亅俀倶
偼弰夞娭悢偲側傞偼偢偱偡丅
丂偙偺峫嶡傪偟偰偄偰丄値師曽掱幃偑桳棟懡崁幃側夝慡懱偱弰夞娭悢傪帩偮側傜偽丄
丂丂倶亖倖(們倧倱(俀兾丒俀倠/倯)丂[倠亖侽丄侾丄丒丒丒丄値亅侾]
丂where 俀n佭亇1丂(倣倧倓丂倯)丄倖 偼丄値亅侾師偺懡崁幃
偲尵偆晽側姶偠偵彂偗傞偺偱偼側偄偐丠偲巚偄偮偒傑偟偨丅傑偩峫嶡偼幭媗傑偭偰偄傑偣傫
偺偱丄帺怣偁傝傑偣傫偗傟偳丏丏丏丅
丂俽乮俫乯偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俀寧侾擔晅偗乯
丂嬻廙偝傫偺乮侾乯偵偮偄偰偺夝朄偼丄彮乆塈墦偱丄
Sylvester峴楍偱5峴5楍偺resultant[兛倷亅(俁兛2亄俆兛亄俈)丆f[兛]丆兛]偐傜妉傑偡丅
丂丂丂丂丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俀寧侾擔晅偗乯
丂丂丂丂丂丂惉掱偱偡両
丂乮俈乯偺乽曽掱幃 倶4亄俆倶3亄俆倶2亅俆倶亅俆亖侽 偵偮偄偰丄f(倶)亖亅倶2亅俀倶 偼弰夞娭悢偲側
傞偼偢偱偡丅乿偵偮偄偰丄
丂冃[兛]亖亅兛2亅俀兛 偱丄兛傪捠傞孮<冃>偺婳摴偼丄
丂丂{亅兛2亅俀兛丆兛3亄俁兛2亅兛亅俆丆亅兛3亅俀兛2亄俀兛丆兛}
偱OK偱偡丅
丂乽倫(倷)亖倷3亅俁俇倷2亄侾俋俆倷亄侾俇侾俋丂偲摼傞丅倫乮倶乯亖侽丂偺夝傪丄兛1丄兛2丄兛3丂偲偡傞偲
偒丄乮俀乯丂兛2 傪丄兛1 偺俀師幃 俥(兛1) 偱昞偣丅乿偵偮偄偰丄乽傕夝乿偼丄
偙傟偵丄倶亖倎倷2亄倐倷亄們亖倶 偲忋婰 倎丄倐丄們 傪戙擖偝偣傞偲丄
丂丂丂F(倷)亖亅(侾俋倷2亅侾俇係俇倷亄俁俆俀侾侽)/俈俆俈
偲偁傝傑偡偑丄惓偟偗傟偽丄倫(亅(侾俋倷2亅侾俇係俇倷亄俁俆俀侾侽)/俈俆俈)傪場悢暘夝偡傞偲丄倫(倷)
偑場悢偵弌尰偡傋偒偱丄偦偆側傜偸偺偱丄壗張偐偵儈僗偑丏丏丏丅
丂巹偑堊偡偲丄
丂{兛丆(亅俈俋兛2亄侾俀俇俇兛亄侾俈俈俆侽)/俈俆俈丆(俈俋兛2亅俀侽俀俁兛亄俋俆侽俀)/俈俆俈}
偲側傝傑偟偨丅
丂乽傕夝乿宆栤戣偺夝寛朄偵乽MA3D5 Galois theory乿偺俉侽暸偺慺捈側敪憐偑嵼傞偺偱丄姎
傒嵱偄偰丄埲壓傪偁傞偲偙傠偵幙栤偟傑偟偨偑...懸偰偳曢傜偣偳夝摎偑偮偒傑偣傫偱偟偨丅
幙栤丂丒丒丒丂A丄B丄C 傪媮傔傞夁掱傪傕偍婅偄偟傑偡丅巼榞偙偦拲帇偝傟徹柧傪両
丂側偤夝摎偑偮偐偸偺偐晄壜夝偱偡........ 惀旕偍婅偄抳偟傑偡丅
丂倫(倷)亖倷3亅俁俇倷2亄侾俋俆倷亄侾俇侾俋丂偵偮偄偰傕丄偙偺庤朄偱両
丂忋偼丄斞崅愭惗偑懱榑偺島媊偺嵟弶偵昁偢庤寁嶼偱堊偟斅彂偟側偝偄丄偲泏惗偵懀偝傟
偨栤偱偡丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俀寧侾擔晅偗乯
丂惓偟偔偼丄丂F(倷)亖亅侾侽(倷亅俁倶亅俀俇)/俈亄俈倶亅俉 偱丄偦偆偡傞偲忋婰偲堦抳偟傑偟偨丅
丂値師曽掱幃偑桳棟懡崁幃側夝慡懱偱弰夞娭悢傪帩偮側傜偽丄偦偺夝偑丄
丂丂丂倶亖f(倵)丂[倵偼丄侾偺尨巒壗偲偐忔崻]丂 f 偼桳棟懡崁幃
傒偨偄偵彂偗傞偺偱偼側偄偐偲媈偭偰偄傑偡偑丂傑偩傑偩峫嶡偑恑傒傑偣傫丅
乽MA3D5 Galois theory乿傪撉傫偱傒傑偡丅
丂搚昅偺巕偝傫偑丄師偺楙廗栤戣偵挧愴偝傟傑偟偨丅乮暯惉俀係擭係寧俇擔晅偗乯
丂乽傕夝乿偺栤戣乮仺丂嶲峫丗乽俽乮俫乯偝傫偐傜偺榖戣乿乯偺偍偐偘偱丄懡崁幃偺僀僨傾儖偺堄
枴偑暘偐偭偰偒傑偟偨丅乮寁嶼偵偼丄Mathmatica ver.8 傪巊偭偰偄傑偡丅乯
楙廗栤戣丂丒丒丒丂倀偝傫偑弌戣偝傟偨栤戣偱偡丅
丂俻忋婛栺側懡崁幃 倶3亅俀倶亅俀 偵偍偄偰丄倶3亅俀倶亅俀 亖侽丂偺崻傪 兛 偲偡傞丅
師偺幃傪兛 偺惍幃偲偟偰昞偣丅
乮侾乯丂乮俆俆亄兛亄俀兛2亄俁兛3亄係兛4亄俆兛5亄俇兛6亄俈兛7乯
丂丂丂/乮侾俋係亄兛亄俉兛2亄俀俈兛3亄俇係兛4亄侾俀俆兛5乯
乮俀乯丂乮侾俋係亄係兛亄侾俇兛2亄俁俀兛3亄係係兛4亄俆俀兛5亄俇侽兛6亄俇俋兛7亄係俇兛8
丂丂丂丂亅侾俁兛9亅係俉兛10亅俀俁兛11亄俇兛12亄俈兛13乯
丂丂丂/乮侾侾俈亅俀兛亅俀俆俉兛2亅係俇俁侽兛3亅俁俈侾係侾兛4
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亅侾俉俉俉俋侽兛5亅侾俆係侽俇俁兛6亄侾俇俁俉係兛7亄俈俉侾俀俆兛8乯
丂傑偢丄乮侾乯偵偮偄偰丄
In[33]:= f[x_] := x^3 - 2*x - 2
In[42]:= PolynomialRemainder[ 55 + 兛 + 2 兛^2 + 3 兛^3 + 4 兛^4 + 5 兛^5
+6 兛^6 + 7 兛^7, f[兛], 兛]
Out[42]= 161 + 167 兛 + 100 兛^2
In[43]:= PolynomialRemainder[194 + 兛 + 8 兛^2 + 27 兛^3 + 64 兛^4 + 125
兛^5, f[兛], 兛]
Out[43]= 748 + 683 兛 + 386 兛^2
(161 + 167 兛 + 100 兛^2)/(748 + 683 兛 + 386 兛^2)
Out[56]= (161 + 167 兛 + 100 兛^2)/(748 + 683 兛 + 386 兛^2)
In[53]:= PolynomialRemainder[ Expand[(748 + 683 兛 + 386 兛^2) (a*兛^2
+ b*兛 + c)], f[兛], 兛]
Out[53]= 1366 a + 772 b + 748 c + (2138 a + 1520 b + 683 c) 兛 + (1520
a +683 b + 386 c) 兛^2
In[57]:= Solve[1366 a + 772 b + 748 c == 1 && 2138 a + 1520 b +
683 c
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 == 0&&1520
a + 683 b + 386 c == 0, {a, b, c}]
Out[57]= {{a -> -(13359/34146782), b -> -(35482/51220173),c ->
141691/51220173}}
In[58]:= a*兛^2 + b*兛 + c /. {a -> -(13359/34146782), b ->-(35482/51220173),c
-> 141691/51220173}
Out[58]= 141691/51220173 - (35482 兛)/51220173 - (13359 兛^2)/34146782
In[61]:= Together[ Expand[{161 + 167 兛 + 100 兛^2}*{141691/51220173 -(35482 兛)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂/51220173
- (13359 兛^2)/34146782}]]
Out[61]= {( 45624502 + 35899590 兛 + 10034815 兛^2 - 13789259 兛^3 -4007700
兛^4)/102440346}
In[62]:= PolynomialRemainder[ 45624502 + 35899590 兛 + 10034815 兛^2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
-13789259 兛^3 - 4007700 兛^4, f[兛], 兛]
Out[62]= 18045984 + 305672 兛 + 2019415 兛^2
In[65]:= Simplify[(18045984 + 305672 兛 + 2019415 兛^2)/102440346]
Out[65]= (18045984 + 305672 兛 + 2019415 兛^2)/102440346
偙傟偑丄摎偊偱偡丅乮俀乯偵偮偄偰偼丄
In[45]:= PolynomialRemainder[ 194 + 4 兛 + 16 兛^2 + 32 兛^3 + 44 兛^4
+ 52兛^5 + 60 兛^6 + 69 兛^7
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 +46 兛^8 - 13 兛^9 - 48 兛^10
- 23 兛^11 + 6 兛^12 + 7 兛^13, f[兛], 兛]
Out[45]= 194
In[46]:= PolynomialRemainder[ 117 - 2 兛 - 258 兛^2 - 4630 兛^3 - 37141 兛^4- 188890 兛^5
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 -154063
兛^6 + 16384 兛^7 + 78125 兛^8, f[兛], 兛]
Out[46]= 117
In[47]:= 194/117
Out[47]= 194/117
偙傟偑丄摎偊偱偡丅
丂俽乮俫乯偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俀寧俀擔晅偗乯
丂乽傕夝乿宆偺栤戣傪婛偵夝偄偨偱偟傚偆偑丄暿偺丄偄傢偽晄曄幃榑帇嵗偐傜丄偡傁偭偲摫弌
偟偨偄偱偟傚偆丅
丂f[倶]=0 丂 E倶丗 倶3 - 倶2 - 4倶 - 1 = 0丂偺夝傪兛偲偡傞偲偒丄X=A兛2+B兛+C伕Q[兛]傪夝偲偡傞
俁師曽掱幃 F[X]=0 偺憂嶌傪両崱夞偺乽傕偺憂傝乿 乽偍嶻乿偵偼壗傜嬯捝傪敽傢側偄丅
丂摫弌夁掱傪柧婰偟丄寢榑傪両偣偭偐偔憂偭偨偺偵岾偐晄岾偐晄曄偱偁偭偨側傜丄
A=__________丄B=_______丄C____________.
偲斞崅愭惗偑恊懓傪尒晳偆偨傃偵恖惗偺桳尷傪幚姶偝傟丄乽傕夝乿宆偺栤戣傕弖帪偵夝寛偟
偨傎偆偑傛偄偲泏惗偵慐傔傜傟偨敪憐偱偡丅
丂忋偺偣偭偐偔憂偭偨偺偵岾偐晄岾偐晄曄偱偁偭偨側傜帇嵗偐傜丄師傕弖帪偵夝偒丄傛傝崅
師偺戙悢曽掱幃偵偮偄偰尋媶偟丄偦偺搘椡偺寢徎傪尋媶幒偺婘忋偵偲斞崅愭惗....丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俀寧俀擔晅偗乯
丂倶3 - 倶2 - 4倶 - 1 = 0丂偵偍偄偰丄倶=併13丒(倲+1/倲)/3+1/3 偲偍偄偰丄
丂丂13(乮併13乯倲6 -5倲3 +併13)/(27倲3)=0丂傛傝丄丂倲3=(5亇3i) / 2併13
丂偦偙偱丄偙傟傪尒偰丄傆偲
丂丂倶+倶5+倶8+倶12丂 where 倶=cos(2兾/13)+ i丒sin(2兾/13)丂傪懪偪崬傫偱傒傞偲丄
丂丂root of 倶3 - 倶2 - 4倶 - 1
丂惿偟偄偑丄晞崋偑堘偆偲偄偆偙偲偼丄椺偊偽丄
丂丂倶+倶5+倶21+倶25丂where 倶=cos(2兾/26)+ i丒sin(2兾/26)
偲偡傟偽丄丂root of 倶3 - 倶2 - 4倶 - 1
丂倶3 - 倶2 - 4倶 - 1 = 0丂偺夝偼丄倶=cos(2兾/26)+ i丒sin(2兾/26)丂傪巊偭偰師偺 倎丄倐丄們 偺傛
偆偵彂偗傞丅
丂倎=倶+倶5+倶21+倶25丂丄倐=倶3+倶11+倶15+倶23丂丄們=倶7+倶9+倶17+倶19
丂倶13=-1丂偵拲堄偟偰丄 倎2=-b-2c+4 傑偨 a+b+c=1 傛傝丄b=倎2-2a-2丂丄 們=-倎2+a+3
偙傟傜偺弰夞娭悢傪妉傑偟偨丅
丂俽乮俫乯偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俀寧俀擔晅偗乯
丂f[X]=X4 + 52X3 - 26X2 - 12X + 1 偲偟丄f[X]=0 偺夝傪兛偲偡傞丅搨撍偱偡偑丄
(1) 冃[兛]=-(64(-1 + 兛)2兛(1 + 兛)4)/(1 - 6兛 + 兛2)4丂傪夝偲偡傞係師曽掱幃傪懡條側敪
丂丂憐偱嶻傫偱壓偝偄丅
丂斀暅偑廳梫側偺偱丄
丂冃2[兛]=冃丒冃[兛]=冃[冃[兛]] 傪偒偪傫偲媮傔偰壓偝偄丅 冃2[兛] 傪夝偲偡傞係師曽掱幃傪
嶻傫偱壓偝偄丅
丂冃3[兛] 傪偒偪傫偲媮傔偰壓偝偄丅冃3[兛] 傪夝偲偡傞係師曽掱幃傪嶻傫偱壓偝偄丅
丂崯張傑偱堊偟丄壗偐偵偍婥偯偒偱偟傚偆両
(2) Q[X]/<f[X]> 偼Q偺惓婯奼戝懱偱偁傞偙偲傪徹柧婅偄傑偡丅
(3) 丂f[X] 偺夝傪兛偲偟傑偟偨偑丄冃[兛]=-(64(-1 + 兛)2兛(1 + 兛)4)/(1 - 6兛 + 兛2)4 傗忋
丂丂偱媮傔偨冃n[兛] 伕Q[兛] (n=2丄3) 偼丄悽奅堦抁偄掕棟 Q(兛)=Q[兛] 偐傜帺柧偲塢傢偢丄
丂丂兛偺俁師埲壓偺懡崁幃昞尰傪懡條側敪憐偱堊偟偰壓偝偄丅乮摫弌夁掱傪柧婰婅偄傑偡乯
冃[兛]=-(64(-1 + 兛)2兛(1 + 兛)4)/(1 - 6兛 + 兛2)4=______________________伕Q[兛]
冃2[兛]=___________________________________________________=______________________伕Q[兛]
冃3[兛]=___________________________________________________=______________________伕Q[兛]
(4) 冃[兛]=-(64(-1 + 兛)2兛(1 + 兛)4)/(1 - 6兛 + 兛2)4=______________________伕Q[兛] 偺嵟塃曈
丂傪兿[兛] 偲偡傞丅値伕N 偵偮偄偰丄兿n[兛]傪慡偰媮傔丄乽傕夝乿偱偁傞偙偲傪徹柧偟偰壓偝偄丅
丂兿2012[兛]傪杮摉偵媮傔丄兿2012[兛] 傪夝偲偡傞係師曽掱幃傪嶻傫偱壓偝偄丅
丂斀暅偑廳梫側椺傪嶲徠偟丄忋傪夝偄偰偔偩偝偄丅慿媦傪懕偗偰傒傑偡丅乮仺丂僇僆僗乯
(巹偺愘偄擔乆偺搳峞払傕敿塱媣揑偵堚暔偲偟偰徚柵偟側偄偺偱偟傚偆偐丠)
丂忋偼丄斞崅愭惗偑懱榑偺島媊偺嵟弶偵島媊偟偨悽奅堦抁偄掕棟丂Q(兛)=Q[兛]
偑嬶懱
椺偱攃埇偑側偝傟偰偄傞偐丄昁偢丂庤寁嶼摍偱堊偟側偝偄偲泏惗偵懀偝傟偨栤偱偡丅
丂埲壓偼丄斞崅愭惗偑懱榑偺島媊偺嵟弶偵島媊偟偨悽奅堦抁偄掕棟丂Q(兛)=Q[兛]
偑嬶
懱椺偱攃埇偑側偝傟偰偄傞偐丄昁偢丂庤寁嶼摍偱堊偟側偝偄偲泏惗偵懀偝傟偨栤偱偡丅
丂崱搙偼丄E倶丗 倶3 - 倶2 - 4倶 - 1 = 0 偺夝傪兛偲偡傞偲偒丄桳棟幃X=(a兛+b)/(兛+c) 伕Q(兛)
傪夝偲偡傞丅
(1)丂俁師曽掱幃 F[X]=0 偺憂嶌傪両崱夞偺乽傕偺憂傝乿乽偍嶻乿偵偼壗傜嬯捝傪敽傢側偄丅
丂丂摫弌夁掱傪柧婰偟丄寢榑傪丗_______________________________________________=0
丂偣偭偐偔憂偭偨偺偵岾偐晄岾偐晄曄偱偁偭偨側傜丄 a=_______丄b=_______丄c________丂偲斞崅愭
惗偑恊懓傪尒晳偆偨傃偵恖惗偺桳尷傪幚姶偝傟丄乽傕夝乿宆偺栤戣傕弖帪偵夝寛偟偨傎偆偑
傛偄偲泏惗偵慐傔傜傟偨敪憐偱偡丅
丂崱夞偺敪憐傪丄岾偐晄岾偐晄曄梫媮偟丄弖帪偵丄乽傕夝乿僎僢僩朄偲柦柤偟傑偡丅
(2)丂忋偺丄偣偭偐偔憂偭偨偺偵岾偐晄岾偐晄曄偱偁偭偨側傜帇嵗偐傜丄師傕丄
丂丂(桳棟幃丂X=(a兛+b)/(兛+c) 伕Q(兛)傪夝偲偡傞乯弖帪偵夝偒丄傛傝崅師偺戙悢曽掱幃偵
丂丂偮偄偰尋媶偟丄偦偺搘椡偺寢徎傪尋媶幒偺婘忋偵偲斞崅愭惗....丅
丂妉偨乽傕夝乿丂冃[兛]亖(a兛+b)/(兛+c)=__________丂偐傜丄冃n[兛] (n伕N) 傪偒偪傫偲媮傔偰壓
偝偄丅偦偟偰丄偦傟傪懡崁幃昞尰偟偰壓偝偄丅Q[兛]伖冃n[兛]=___________.
(3)丂岾偐晄岾偐晄曄梫媮偟丄弖帪偵乽傕夝乿僎僢僩朄偱丄搶戝偺栤戣偑弖帪偵乮___昩偱乯夝偗
丂丂偨姶憐傪婰偟丄
(4)丂搶戝偺栤戣偺愝栤偺巇曽偑偄偨偩偗側偄揰傪偁偘偰夝愢婅偄傑偡丅
丂岾偐晄岾偐晄曄梫媮偟丄弖帪偵乽傕夝乿僎僢僩朄側傞傾儞僌儖偼擛壗偱偟偨偐丠
丂乽俻忋婛栺側懡崁幃 倶3亅俀倶亅俀 偵偍偄偰丄倶3亅俀倶亅俀 亖侽丂偺崻傪 兛 偲偡傞乿偲偄偆偙偲
偼丄兛偼丄俻忋戙悢揑側尦偱偁傝丄傑偨丄丂俥乮倶乯亖倶3亅俀倶亅俀丂偲偍偔偲丄丂俥乮倶乯丒俻乵倶乶丂偼懡
崁幃娐 俻乵倶乶丂偺僀僨傾儖偵側傞丅乮仼懡崁幃娐 俻乵倶乶丂偼扨崁僀僨傾儖堟偱偁傞偺偱丄婛
栺懡崁幃 俥乮倶乯 偵傛傝惗惉偝傟傞両乯
丂偙偺偲偒丄丂彜娐 俻乵倶乶/乮俥乮倶乯丒俻乵倶乶乯亖俻乵兛乶亖俻乮兛乯丂偑惉傝棫偮丅
偙偺庤朄偵傛傝丄偄傠偄傠側 俻 偺桳尷奼戝懱傪峔惉偡傞偙偲偑偱偒傞丅
丂偙偺峫偊曽偵傛傝丄倀偝傫偼偄傠偄傠側栤戣偵挧愴偝傟偨丅
栤戣侾丂丂倶7亖侾丂乮偨偩偟丄倶 亗 侾乯偺偲偒丄
丂丂丂![]()
丂偺幃偺抣傪媮傔傛丅乮墶昹巗棫戝妛乯
丂偙偺栤戣偵懳偟偰壗傕峫偊偢偵庴尡悢妛晽偵夝偗偽丄師偺傛偆偵側傞偱偁傠偆丅
乮夝乯丂梌幃亖乮倶亄倶2亄倶4亄倶5乯/乮侾亄倶2亄倶4亄倶6乯亄倶3/乮侾亄倶6乯
丂丂丂丂丂丂亖乮倶亄倶2亄倶3亄倶4亄俀倶5亄俀倶7亄倶8亄倶9亄倶10亄倶11乯/乮侾亄倶2亄倶4亄俀倶6亄倶8亄倶10亄倶12乯
丂丂丂丂丂丂亖乮倶亄倶2亄倶3亄倶4亄俀倶5亄俀亄倶亄倶2亄倶3亄倶4乯/乮侾亄倶2亄倶4亄俀倶6亄倶亄倶3亄倶5乯
丂丂丂丂丂丂亖俀乮侾亄倶亄倶2亄倶3亄倶4亄倶5乯/乮侾亄倶亄倶2亄倶3亄倶4亄倶5亄俀倶6乯
丂丂丂偙偙偱丄丂倶7亖侾丂傛傝丄丂侾亄倶亄倶2亄倶3亄倶4亄倶5亄倶6亖侽丂側偺偱丄
丂丂丂丂丂丂丂丂梌幃亖亅俀倶6/倶6亖亅俀
丂丂丂偲側傞丅乮廔乯
丂偙偺栤戣傪丄倀偝傫偼丄 俻乵倶乶/乮俥乮倶乯丒俻乵倶乶乯亖俻乵兛乶亖俻乮兛乯
偲偄偆偙偲傪堄幆偟偰師偺
傛偆偵夝偐傟偨丅
乮夝乯丂俻乵倶乶/乮俥乮倶乯丒俻乵倶乶乯偵偍偄偰丄丂侾亄倶2丂丄侾亄倶4丂丄侾亄倶6丂偺媡尦偼丄倶 偺懡崁幃
丂丂丂偱昞偝傟傞丅丂幚嵺偵丄侾亄倶亄倶2亄倶3亄倶4亄倶5亄倶6亖侽丂偵拲堄偟偰丄
丂丂丂丂丂乮侾亄倶2乯乮侾亄倶亄倶4亄倶5乯亖侾
丂丂丂丂丂乮侾亄倶4乯乮侾亄倶亄倶2亄倶3乯亖侾
丂丂丂丂丂乮侾亄倶6乯乮侾亄倶亄倶3亄倶5乯亖侾
丂丂丂偑惉傝棫偮偺偱丄
丂丂丂丂梌幃亖倶乮侾亄倶亄倶4亄倶5乯亄倶2乮侾亄倶亄倶2亄倶3乯亄倶3乮侾亄倶亄倶3亄倶5乯
丂丂丂丂丂丂丂亖倶亄倶2亄倶5亄倶6亄倶2亄倶3亄倶4亄倶5亄倶3亄倶4亄倶6亄倶8
丂丂丂丂丂丂丂亖俀乮倶亄倶2亄倶3亄倶4亄倶5亄倶6乯
丂丂丂丂丂丂丂亖亅俀
乮僐儊儞僩乯丂榬椡偱夝偄偨応崌偵斾傋丄壗偐僗僢僉儕偟偨夝摎偱旤偟偄偱偡偹両傗偼傝丄悢妛
丂丂丂丂丂丂偺栤戣偼杮幙傪尒嬌傔偰偄傟偽旤偟偔夝偗傞傛偆偵弌棃偰偄傞偺偱偟傚偆両
丂偙偺帇揰偵棫偭偰丄愭偺栤戣傪嵞峫偟偰傒傛偆丅
椺乮嵞宖乯丂俻忋婛栺側懡崁幃 倶3亅俀倶亅俀 偵偍偄偰丄倶3亅俀倶亅俀 亖侽丂偺崻傪 兛 偲偡傞丅
丂丂偙偺偲偒丄丂兛/乮侾亄兛乯丂傪丄兛 偺惍幃偲偟偰昞偣丅
乮夝乯丂俥乮倶乯亖倶3亅俀倶亅俀丂偲偟偰丄丂俻乵倶乶/乮俥乮倶乯丒俻乵倶乶乯偵偍偄偰丄
丂丂丂乮侾亄倶乯乮亅侾亅倶亄倶2乯亖亅侾亅倶亄倶2亅倶亅倶2亄倶3亖亅侾亅俀倶亄俀倶亄俀亖侾
丂丂傛傝丄侾亄倶 偺媡尦偼丄丂亅侾亅倶亄倶2丂偱偁傞丅
丂丂丂傛偭偰丄
丂梌幃亖兛丒乮亅侾亅兛亄兛2乯亖亅兛亅兛2亄兛3亖亅兛亅兛2亄俀兛亄俀亖俀亄兛亅兛2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮廔乯
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽倸倠係俁乿偝傫偐傜偺僐儊儞僩偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俁擭侾侽寧侾侽擔晅偗乯
丂栤戣侾 傪丄丂1/(倶亄侾/倶)亄1/(倶2亄侾/倶2)亄1/(倶3亄侾/倶3)亖亅俀丂偲彂偒側偍偟偰丄
倶亖倕2兾i/7丂偲偡傞偲丄梋尫偺媡悢榓偵側傞偺偱丄僄僋僙儖偱寁嶼偟偰傒傑偟偨丅
丂偡傞偲丄値 傪婏悢丄倶亖倕2m兾i/n丄(倣丆値)亖侾丂偲偟偰丄
丂丂1/(倶亄侾/倶)亄1/(倶2亄侾/倶2)亄丒丒丒亄1/(倶(値-1)/2亄侾/倶(値-1)/2)
丂亖倶/(侾亄倶2)亄倶2/(侾亄倶4)亄丒丒丒亄倶(n-1)/2/(侾亄倶n-1)
偺抣偼丄値佭侾丂(倣倧倓丂係)丂偺偲偒丄丂(値亅侾)/係
丂丂丂丂丂値佭俁丂(倣倧倓丂係)丂偺偲偒丄丂亅(値亄侾)/係
偲堦斒壔偝傟傞傒偨偄偱偡丅僄僋僙儖寁嶼側偺偱丄徹柧偼暘偐傝傑偣傫丅
乮惓尫傗梋尫偺媡悢榓偺岞幃偭偰偁偭偨偱偟傚偆偐丠乯
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侽寧侾侽擔晅偗乯
丂忋婰偺倸倠係俁偝傫偺寢壥偑偲偰傕嫽枴怺偐偭偨偺偱丄偪傚偭偲寁嶼偟偰傒偨偲偙傠丄偆傑偔徹
柧偱偒傑偟偨丅
丂帵偡偙偲偼丄丂儼[k=1丆n] 1/(倶k亄侾/倶k)亖値/俀丂丂偨偩偟丄値佭1丂(倣倧倓丂係)丂偺偲偒
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖亅値/俀丂丂偨偩偟丄値佭俁丂(倣倧倓丂係)丂偺偲偒
偲摨抣偵側傝傑偡丅乮倠亖値 偺偲偒丄侾/俀 偱丄倠亙値 偺偲偒偑忋偺抣偺俀偮暘偵憡摉偡傞偨傔乯
丂倣 偲 値 偑慺側傜偽丄倣亖侾偩偗峫偊傟偽丄懠偺偲偒偼崁傪暲傋懼偊偨偩偗側偺偱徣棯偱
偒傑偡丅偡側傢偪丄
丂丂倶k亄侾/倶k亖俀們倧倱乮俀兾/値)
偲峫偊傑偡丅們倧倱兤偺 値 攞妏偺岞幃偐傜丄夝偲學悢偺娭學傪巊偊偽丄媡悢榓傪媮傔傞偙偲
偑偱偒傑偡丅偡側傢偪丄(們倧倱兤亄倝丒倱倝値兤)値亖侾 傪揥奐偟偰幚悢晹暘傪庢傝弌偟偰丄
倱倝値2兤亖侾亅們倧倱2兤丂偲偟偨偲偒偵丄們倧倱兤偺嶌傞 値 師曽掱幃偵拲栚偟偰丄
丂夝偺媡悢榓亖(們倧倱兤偺侾師偺學悢)/(亅掕悢崁)亖値丒倝n-1 傪摼傑偡丅偙傟傪巊偆偲丄峆摍
幃偺徹柧偑姰椆偡傞偲巚偄傑偡丅
丂偙偺傛偆側捈愙挷傋傞偺偑戝曄側峆摍幃偵偮偄偰丄攚宨偑暘偐傞偲偆傟偟偄婥暘偵側傝傑
偡偹丅
丂倸倠係俁偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侽寧侾侽擔晅偗乯
丂嬻廙偝傫丄偍曉帠偁傝偑偲偆偛偞偄傑偡丅僈儘傾惗抋俀侽侽擭偲偄偆偙偲偱丄僈儘傾棟榑傪偍
偝傜偄偟偰偄偰丄偨傑偨傑摉僒僀僩偺婰弎傪尒偮偗偰峫偊偰傒偨師戞偱偡丅
丂暋慺悢傪帩偪弌偟偰峫偊傑偟偨偑丄婛栺懡崁幃丂侾亄倶亄倶2亄丒丒丒亄倶n-1丂傪巊偭偨奼戝
懱偺拞偱峫偊傞偲偐丄扨埵墌偵愙偡傞惓値妏宍傪峫偊偰丄弶摍婔壗偱徹柧偡傞偲偐傕偁傞
偐偲巚偄傑偡偑丄崱偼暘偐傝傑偣傫丏丏丏丅
丂俥俶偝傫偐傜偺懕曬偱偡丅乮暯惉俀俁擭侾侽寧侾俀擔晅偗乯
丂倶/(侾亄倶2)亄倶2/(侾亄倶4)亄丒丒丒亄倶(n-1)/2/(侾亄倶n-1)
偺抣偼丄値佭侾丂(倣倧倓丂係)丂偺偲偒丄丂(値亅侾)/係
丂丂丂丂丂値佭俁丂(倣倧倓丂係)丂偺偲偒丄丂亅(値亄侾)/係
偵偮偄偰丄乽桳尷奼戝懱偺惈幙乿偺偲偙傠偵偁傞 値=7 偺偲偒偺徹柧偺傗傝偐偨偺傑傑偱傗偭
偰傒傑偟偨丅値 偑慺悢偺偲偒偼偱偒傑偟偨丅徹柧偺搒崌偱彮偟偩偗曄偊傑偟偨丅
丂崁悢偑 (値-1)/2 側偺傪丄屻偺 (値-1)/2 崁傪偮偗偰値-1崁偵偟傑偟偨丅嬻廙偝傫偺幃偲傕彮
偟偩偗堘偄傑偡丅傕偪傠傫幚幙揑偵偼摨偠偱偡丅
乮徹柧乯丂倫 傪婏慺悢偲偟丄倶 傪 1 偺尨巒倫忔崻偲偡傞丅偙偺偲偒丄
丂Z=倶/(侾亄倶2)亄倶2/(侾亄倶4)亄丒丒丒亄倶倫-1/(侾亄倶2(倫-1))丂偺抣偼丄
丂倫佭侾丂(倣倧倓丂係)丂偺偲偒丄丂(倫亅侾)/俀
丂倫佭俁丂(倣倧倓丂係)丂偺偲偒丄丂亅(倫亄侾)/俀
偱偁傞偙偲傪帵偡丅(倫-1)/2=倣 偲偍偔偲丄倫=2倣+1偱丄倶2倣+1=1丂偐偮丄1+倶+倶2+ゥゥ+倶2倣=0
丂傑偢丄倱偑倫偱妱傟側偄偲偒丄(1+倶s)(1+倶2s+倶4s+ゥゥ+倶2ms乯=1丂偑惉傝棫偮丅
幚嵺偵丄嵍曈偼丄1+倶s+倶2s+倶3s+倶4s+ゥゥ+倶2ms+倶(2m+1)s 偲側傞偑丄嵟屻偺崁偼1偱丄
倶s丄倶2s丄倶3s丄倶4s丄丒丒丒丄倶2ms丂偼慡懱偲偟偰丄倶丄倶2丄ゥゥ丄倶2倣丂偱偁傞偐傜丄偙傟傜偵1傪壛
偊偰0丄廬偭偰丄慡晹偱1偵側傞丅偙偺偲偒丄1/(1+倶s)=1+倶2s+倶4s+ゥゥ+倶2ms=儼(k=0乣m) 倶2ks
偩偐傜丄
Z=儼(s=1乣2m) 倶s/(1+倶2s)=儼(s=1乣2m) 倶s儼(k=0乣m) 倶4ks=儼(s=1乣2m丆k=0乣m) 倶(4k+1)s
丂倫佭俁丂(倣倧倓丂係)丂偺偲偒丄4k+1佭0 (倣倧倓丂倫)丂偲側傞偙偲偼側偄偐傜丄
擟堄偺 倲 (1亝t亝2m) 偲 倠 (0亝k亝m) 偵懳偟偰丄(4倠+1)倱=倲丂偲側傞 倱
((1亝倱亝2m)丂偑堦堄
揑偵掕傑傞丅廬偭偰丄儼(s=1乣2m丆k=0乣m) 倶(4k+1)s丂偵偍偄偰丄倶t (1亝t亝2倣)偼偡傋偰挌
搙 倣+1屄尰傟傞丅倶0=1 偼堦搙傕尰傟側偄丅
丂廬偭偰丄丂Z=(倣+1)(倶+倶2+ゥゥ+倶2倣)=(倣+1)(-1)=-(倣+1)=-(倫+1)/2
丂倫佭侾丂(倣倧倓丂係)丂偲偡傞丅丂倠=倣/2 偺偲偒丄4倠+1佭0 (倣倧倓丂倫)丂偲側傞丅
偦傟埲奜偵丄4倠+1佭0 (倣倧倓丂倫)丂偲側傞偙偲偼側偄丅
丂擟堄偺 倲 (1亝t亝2m) 偲 倠 (0亝k亝m丄倠亗倣/2) 偵懳偟偰丄(4倠+1)s=t丂偲側傞
s ((1亝倱亝2倣)
偑堦堄揑偵掕傑傞丅廬偭偰丄倶t (1亝t亝2倣)偼偡傋偰挌搙倣屄尰傟傞丅倶0=1 偼丄倠=倣/2 偺
偲偒偩偐傜丄2倣屄尰傟傞丅
丂廬偭偰丄丂Z=倣(倶+倶2+ゥゥ+倶2倣)+2倣=-倣+2m=倣=(倫-1)/2丂丂乮徹廔乯
丂傕偆彮偟惛枾側丄廬偭偰丄柺搢側媍榑傪偡傟偽慺悢偱側偄偲偒傕偱偒偦偆側婥偑偟傑偡丅偱
傕曽朄傪曄偊傞曽偑偄偄傛偆偱偡丅
丂俥俶偝傫偐傜偺懕曬偱偡丅乮暯惉俀俁擭侾侽寧侾俁擔晅偗乯
丂乽桳尷奼戝懱偺惈幙乿偵偁傞傕偲傕偲偺栤戣侾傪彮偟曄偊偰傒傑偟偨丅
丂倶7亖侾丂乮偨偩偟丄倶亗侾乯丂偺偲偒丄倶/(倶2-1)+倶2/(倶4-1)+倶3/(倶6-1)丂偺幃偺抣傪媮傔傛丅
偟偐偟丄偙傟偼鉟楉側抣偵側傝傑偣傫丅偦偙偱傕偆彮偟曄偊偰傒傑偟偨丅
丂倶7亖侾丂乮偨偩偟丄倶亗侾乯丂偺偲偒丄倶/(倶2-1)+倶2/(倶4-1)-倶3/(倶6-1)丂偺幃偺抣傪媮傔傛丅
丂摎偼丄0偵側傝傑偡丅晛捠偵寁嶼偡傟偽偱偒傑偡丅扨側傞寁嶼偱暿偵柺敀偔傕偁傝傑偣傫丅
偟偐偟丄婔壗妛揑側堄枴偑偁傝傑偡丅倶/(倶2-1)=1/(倶-1/倶) 摍偱偡偑丄暋慺暯柺偱偺扨埵墌
傪峫偊偨偲偒丄倶-1/倶丄倶2-1/倶2 摍偼扨埵墌偵撪愙偡傞惓俈妏宍偺懳妏慄偺挿偝偵 倝 傪偐
偗偨傕偺偵側傝傑偡丅
丂廬偭偰丄忋偺幃偼惓俈妏宍偺懳妏慄(曈傪娷傓)偺挿偝偺媡悢偵娭偡傞娭學幃偵側傝傑偡丅
偙傟偼乽惓俈妏宍偺偁傞惈幙乿偵偁傞 乽1/a=1/b+1/c乿偱偡丅偝偰丄偙偺娭學丄懄偪丄忋偺幃
偱偡偑丄偙傟偼堦斒壔偱偒傞偱偟傚偆偐丅
丂傑偢丄値=11偺偲偒偵帡偨傛偆側娭學偑惉傝棫偮偱偟傚偆偐丠
丂俥俶偝傫偐傜偺懕曬偱偡丅乮暯惉俀俁擭侾侽寧侾係擔晅偗乯
丂値=11偺偲偒偼丄偳偆傗傜柍棟傒偨偄偱偡丅値=7偩偗偺屒棫偟偨尰徾側偺偱偟傚偆偐丅傕偆
彮偟娙扨側偙偲傪峫偊偰傒傑偡丅
丂倶傪1偺尨巒7忔崻偲偡傞偲偒丄A=倶+倶2+倶4丂丄B=倶3+倶5+倶6丂偺抣傪媮傔傛丅
丂傕偲傕偲偺栤戣丂Z=倶/(侾亄倶2)亄倶2/(侾亄倶4)亄倶3/(倶6 + 1) 偼桳棟悢偱偟偨丅
丂偙傟偼丄Galois奼戝Q(倶)/Q偺Galois孮(埵悢俇偺弰夞孮)偺1偮偺惗惉尦冃丗倶仺倶3丂偵傛偭
偰Z偑晄曄偱偁傞偐傜偱偡丅A丄B偼丄冃(A)=B丄冃(B)=A 傪枮偨偟傑偡偐傜丄桳棟悢懱Q偺尦
偱偼偁傝傑偣傫丅冃2偱晄曄偱偡偐傜丄Q忋俀師偺懱偺尦偵側傝傑偡丅偡側傢偪丄桳棟悢偲併
傪1偮巊偭偰偐偗傑偡丅傕偪傠傫丄偙傫側偙偲偼抦傜側偔偰晛捠偵夝偗傑偡丅夝偄偰傒偰偔偩偝
偄丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侽寧侾係擔晅偗乯
丂乽倶7亖侾丂乮偨偩偟丄倶亗侾乯偺偲偒丄倶/(倶2-1)+倶2/(倶4-1)-倶3/(倶6-1)丂偺幃偺抣傪媮傔傛丅乿
偼丄師偺傛偆偵彂偄偨曽偑帺慠偱偟傚偆丅
丂倶7亖侾丂乮偨偩偟丄倶亗侾乯丂偺偲偒丄倶/(倶2-1)+倶2/(倶4-1)+倶4/(倶8-1)丂偺幃偺抣傪媮傔傛丅
丂儐乕僋儕僢僪偺屳彍朄側偳偱丄倶6+倶5+倶4+倶3+倶2+倶+1 傪朄偲偡傞媡尦傪峫偊傞偲丄椺偊偽丄
P(倶)=1+2倶2+3倶4+4倶6+5倶8+6倶10+7倶12丂偵傛偭偰丄(1-倶2)丒P(倶)=-7丂傪摼傞偙偲偑偱偒傑偡丅
倶丒P(倶)+倶2丒P(倶2)+倶4丒P(倶4) 傪寁嶼偡傞偲丄倶6+倶5+倶4+倶3+倶2+倶+1 偺掕悢攞偲側傝丄0傪摼傑偡丅
丂摨偠傛偆偵寁嶼偡傞偲丄
丂倶15亖侾丂乮偨偩偟丄倶亗侾乯丂偺偲偒丄倶/(倶2-1)+倶2/(倶4-1)+倶4/(倶8-1)+倶8/(倶16-1)丂偺抣偑 0
偵側傞偙偲傕妋擣偱偒傑偟偨丅嶰妏娭悢傪巊偭偰峫偊傞偙偲傕帋偟偰傒傑偟偨偑丄偆傑偔偱偒傑
偣傫偱偟偨丅
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侽寧侾係擔晅偗乯
丂堦斒壔偱偒傞傛偆偱偡偹丅
丂倶2値-1亖侾丂乮偨偩偟丄倶亗侾乯丂偺偲偒丄
丂丂丂倶/(倶2-1)+倶2/(倶4-1)+倶4/(倶8-1)+丒丒丒+倶2値-1/(倶2値-1)=0
丂倶/(倶2-1)+倶2/(倶4-1)+倶4/(倶8-1)+丒丒丒+倶2値-1/(倶2値-1)=x(1+倶+倶2+ゥゥ+倶2n-2)/(倶2値-1)丂偑惉
傝棫偮傛偆偱偡丅悢妛揑婣擺朄偱徹柧偱偒偦偆偱偡丅
丂俥俶偝傫偐傜偺懕曬偱偡丅乮暯惉俀俁擭侾侽寧侾俇擔晅偗乯
丂倶傪1偺尨巒7忔崻偲偡傞偲偒丄A=倶+倶2+倶4丂丄B=倶3+倶5+倶6丂偺抣傪媮傔傛丅
偵偮偄偰丄倶 偑1偺尨巒7忔崻偲偄偆偩偗偱偼丄A丄B偺抣偼妋掕偟傑偣傫偱偟偨丅A丄B偺抣傪
妋掕偡傞偨傔偵偼丄倶 傪摿掕偡傞昁梫偑偁傝傑偡丅
丂倶=cos(2兾/7)+倝丒sin(2兾/7)偺偲偒丄A=倶+倶2+倶4丂丄B=倶3+倶5+倶6丂偺抣傪媮傔傛丅
栤戣偲偟偰偳偪傜偺曽偑偄偄偐偼旝柇偱偡丅側偍丄尦偺栤戣丄偡側傢偪丄栤戣侾偺俀偮偺夝
摎偵偮偄偰偱偡偑丄暘悢偲峫偊傟偽丄捠暘傪偡傞慜偵暘曣偺桳棟壔傪偡傞偺偑惓偟偄偺偱
(倶2+1)(1+倶+倶4+倶5)=1摍傪巊偭偰暘曣傪桳棟壔偡傞傋偒偱偡偑丄偙傟偵婥偑偮偔偺偼晛捠偼
柍棟偐側偲巚偄傑偡丅
丂暘悢幃偲峫偊傟偽丄捠暘偡傞偟偐側偄偲偙傠偱偟傚偆丅偁傞偄偼丄嵟屻偺崁傪 倶4/(倶+1) 偲偟
偰偐傜捠暘偐傕偟傟傑偣傫偑丏丏丏丅妋偐偵棟榑揑偵偼丄暘曣偺桳棟壔傪偟偨曽偑偄偄偲偼
巚偄傑偡丅
丂師偺栤戣俀偵偮偄偰偱偡偑丄(1+倶3)(1+倶+倶2)=1 傕惉傝棫偪傑偡偐傜丄暘曣偺桳棟壔偵傛傞
曽朄偱傕摨偠條偵偱偒傑偡丅
栤戣俀丂丂倶5亖侾丂乮偨偩偟丄倶 亗 侾乯偺偲偒丄
丂丂丂![]()
丂偺幃偺抣傪媮傔傛丅乮戝嶃栻壢戝妛乯
丂偙偺栤戣偵懳偟偰壗傕峫偊偢偵庴尡悢妛晽偵夝偗偽丄師偺傛偆偵側傞偱偁傠偆丅
乮夝乯丂
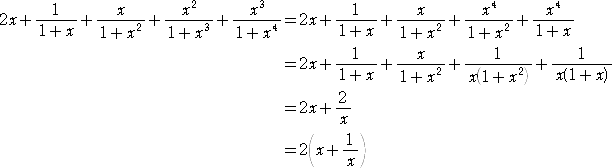
侾亄倶亄倶2亄倶3亄倶4亖侽丂傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂![]()
傛偭偰丄
丂丂丂丂丂丂丂![]()
偙偺俀師曽掱幃傪夝偄偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂![]()
傛偭偰丄
丂丂丂丂丂丂丂![]()
偲側傞丅乮廔乯
丂偙偺応崌丄幃偺抣偼俀偮懚嵼偡傞丅偟偐傕俀悢偼屳偄偵嫟栶偱偁傞丅
倀偝傫偐傜偺帹婑傝忣曬偵傛傟偽丄嫟栶偼丄愄偼嫟鏱偲彂偄偰偄偨偦偆偱偁傞丅乮巹偼丄嫟栶
偱嫵傢偭偨悽戙偱偡両乯丂乽鏱乿偼擄偟偄帤偱偁傞偑丄孭撉傒偱偼乽偔傃偒乿偲撉傓丅攏幵偱攏
傪擇摢墶偵偮側偖偲偒偵巊偆朹偺偙偲偱丄俀偮偺抣偑侾偮偺懳偲側偭偰摥偔條巕偑栚偵晜偐傇
傛偆側愨柇側栿岅偱偁偭偨丅偟偐偟丆忢梡娍帤奜偱偁偭偨偨傔丄壒偩偗偲偭偰嫟栶偲彂偐傟傞
傛偆偵側傝丄崱偱偼堄枴偑傛偔暘偐傜側偄傕偺偲側偭偰偟傑偭偨丅乮巆擮両両乯
丂忋婰偺栤戣偵懳偟偰丄
丂丂丂丂丂乮侾亄倶乯乮侾亄倶2亄倶4乯亖侾
丂丂丂丂丂乮侾亄倶2乯乮侾亄倶3亄倶4乯亖侾
丂丂丂丂丂乮侾亄倶4乯乮侾亄倶亄倶3乯亖侾
偑惉傝棫偮偺偩偑丄偙偺応崌丄庴尡悢妛晽側夝偵彑傞傛偆側夝朄偑巚偄偮偐側偄両
偒偭偲丄偙偺応崌偼丄摿庩側偺偩傠偆丏丏丏丅
栤戣俁丂丂俻忋婛栺側懡崁幃 倶3亄倃亄侾丂偺楇揰傪 兤 偲偡傞偲偒丄懱 Q(兤) 偺尦丂侾亄兤2
丂丂丂丂丂偺僲儖儉傪寁嶼偣傛丅乮弌揟丗van der Waerden 挊丂Moderne Algebra乯
乮倀偝傫偼丄偙偆昞尰偡傋偒栤傪丄崅峑偱偼攚宨傪屘堄偵塀摻偟偰偄傞偲扱偄偰偍傜傟傑偡丅乯
丂偙偙偱丄懱 Q(兤) 偺尦 兞 偺僲儖儉偲偼丄Q(兤) 偺婎掙傪 乷倴1丆倴2丆丒丒丒丆倴値乸 偲偡傞偲偒丄
丂丂丂丂丂丂丂丂丂丂丂兞丒乮倴1丆倴2丆丒丒丒丆倴値乯亖乮倴1丆倴2丆丒丒丒丆倴値乯俙
偱掕傑傞 値 師偺惓曽峴楍 俙 偺峴楍幃偺抣傪偄偆丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂俶乮兞乯亖倓倕倲 俙
丂偙偺偙偲傪妋擣偟偰丄栤戣傪夝偄偰傒傛偆丅
乮夝乯丂兞亖侾亄兤2丂偲偍偔丅丂兤3亄兤亄侾亖侽丂側偺偱丄Q(兤) 偺婎掙偲偟偰丄乷侾丆兤丆兤2乸
丂偲偡傞偲偒丄丂丂兞丒侾亖侾亄兤2
丂丂丂丂丂丂丂丂丂丂兞丒兤亖兤亄兤3亖兤亅兤亅侾亖亅侾
丂丂丂丂丂丂丂丂丂丂兞丒兤2亖兤2亄兤4亖兤2亄兤丒兤3亖兤2亄兤丒乮亅兤亅侾乯亖亅兤
丂傛偭偰丄丂丂兞丒乮侾丆兤丆兤2乯亖乮侾丆兤丆兤2乯俙
丂丂丂丂丂丂丂丂丂丂丂丂丂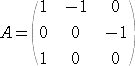
偲彂偗傞偺偱丄丂懱 Q(兤) 偺尦丂侾亄兤2 偺僲儖儉偼丄丂倓倕倲俙亖侾丂偱偁傞丅乮廔乯
乮曗懌乯丂倓倕倲乮兞俤亅俙乯亖侽丂偐傜丄兞傪夝偵帩偮曽掱幃 兞3亅兞2亅侾亖侽 偑惗惉偝傟傞丅
丂丂丂丂偙偺偲偒丄丂兞 偺僲儖儉偼丄曽掱幃 兞3亅兞2亅侾亖侽 偵偍偗傞夝偲學悢偺娭學偐傜丄
丂丂丂丂丂丂丂俁偮夝偺愊亖亅乮亅侾乯/侾亖侾
丂丂丂偲媮傔偰傕傛偄丅
丂嬻廙偝傫偑丄椺偺梊憐偵偮偄偰峫嶡偝傟傑偟偨丅乮暯惉俀係擭俀寧俁擔晅偗乯
丂桳棟學悢値師曽掱幃偑桳棟懡崁幃側夝慡懱偱弰夞娭悢傪帩偮側傜偽丄偦偺夝偼丄
丂丂倶=f(倵)丂[倵偼丄e2兾i/k]丂 f 偼桳棟懡崁幃丄倠 偼偁傞帺慠悢
偺傛偆側宍偱彂偗傞偺偱偼側偄偐偲媈偭偰偄傑偡丅偟偽傜偔偺娫丄乽椺偺梊憐乿偲柤晅偗偰傒
傑偡丅崱夞偼丄摿偵丄値=2 偺応崌偵偮偄偰峫嶡偟傑偟偨丅
丂値=2 偺帪偼丄偄偮偱傕弰夞娭悢偲側傝傑偡偑丄(倶2+倎倶+倐 偵懳偟偰丄倎-倶)
偄偮偱傕丄倶=f(倵) [倵偼1偺尨巒壗偲偐忔崻]偲彂偗傞偨傔偵偼丄掕悢崁丄掕悢攞傪屻晅偗偡
傟偽丄偁傜備傞併m偨偪偑丄倶=f(倵) [倵偼1偺尨巒壗偲偐忔崻]偲偄偆宍偱峔惉偱偒傟偽傛偄
傢偗偱偡丅
丂併乮-1乯偼丄倶偺4忔崻偦偺傕偺偱丄併2丄併乮-2乯偼丄倶偺8忔崻倵偵傛偭偰丄w+1/w傗w+w3 偱
峔惉偱偒傑偡丅
丂倫偑婏慺悢偺帪丄倫忔崻偺揔摉側懡崁幃傪偲傞偲丄埲壓偺傛偆偵偟偰丄併p 偁傞偄偼併乮-p乯
傪峔惉偱偒傑偡丅倫k [倠=1丄2丄丒丒丒丄値-1]偨偪傪暯曽忚梋偺堘偄偱丄A丄B偵暘偗丄
丂丂A=儼倫k [暯曽忚梋払]丂丄丂B=儼倫k [旕暯曽忚梋払]
丂A丄B傪夝偲偡傞俀師曽掱幃 F(X) 傪峫偊傑偡偲丄丂A+B=-1丂偱偁傝丄
丂(倫-1)/2 偑嬼悢[偮傑傝丄倫=4N+1]偺偲偒偵偼丄-1偑暯曽忚梋偱偁傝丄A2=(N-1)A+NB+2N 偲
側傝丄 AB=-A-A2=-N(A+B)-2N=-N
丂傛偭偰丄F(X)=X2+X-N 偱偁傝丄 A丄B=(-1亇併乮1+4N乯)/2=(-1亇併p)/2
丂(倫-1)/2 偑婏悢[偮傑傝丄倫=4N-1]偺偲偒偵偼丄-1偼旕暯曽忚梋偱偁傝丄A2=(N-1)A+NB 偲
側傝丄丂AB=-A-A2=-N(A+B)=N
丂傛偭偰丄F(X)=X2+X+N 偱偁傝丄 A丄B=(-1亇併乮1-4N乯)/2=(-1亇併乮-p乯)/2
丂4倫忔崻偺懡崁幃偵傛偭偰丄併倫偁傞偄偼併乮-倫乯偺傕偆堦曽傪摼傞偙偲偑偱偒傑偡丅
乮A-B傪暋慺悢暯柺忋偱90搙夞揮偝偣傟偽椙偄偐傜乯
丂崌惉悢偵偮偄偰偼丄併乮倫倯乯傪夝偵娷傓曽掱幃傪嶌傞偵偼丄椺偊偽丄併乮35乯偺応崌丄師偺
傛偆偵丄
丂丂A=倶+倶3+倶9+1/倶+1/倶3+1/倶9亖併7 where 倶=cos(2兾/28)+i丒sin(2兾/28)
丂丂B=倷+倷4-1= 1/2+併5/2
丂丂C=倷2+倷3-1= 1/2-併5/2 where 倷=cos(2兾/5)+i丒sin(2兾/5)
丂偙傟傜偐傜丄AB-AC偱丄併乮35乯傪峔惉偱偒傑偡丅AB-AC偼丄1偺140忔崻偺揔摉側懡崁幃
偱昞偝傟傞...偲偄偆晽偵偟偰丄倫丄倯傪尦偵峔惉偡傟偽椙偄偱偡丅
丂埲忋偐傜丄桳棟學悢偺俀師曽掱幃偺夝偼丄
丂丂倶=f(倵) [w偼1偺尨巒壗偲偐忔崻]丂 f 偼桳棟懡崁幃
偲偄偆宍偱昞偡偙偲偑偱偒傞偲偄偆偙偲偑帵偝傟偨偲巚偄傑偡丅俁師偱偼峫嶡偑擄偟偔側傝偦偆
側梊姶丏丏丏丅
丂FN偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俀寧俁擔晅偗乯
丂弰夞娭悢傪傕偮偲偒偲偄偆偺偼弰夞奼戝偺応崌偱丄弰夞奼戝偼傾乕儀儖奼戝偱偡偐傜丄僋
儘僱僢僇乕偺掕棟偺摿庩側応崌偵側傝傑偡丅
僋儘僱僢僇乕偺掕棟
丂桳棟悢懱忋偺傾乕儀儖奼戝懱偼丄偁傞墌暘奼戝懱Q(e2兾i/k)偵娷傑傟傞丅
丂摿庩側応崌偲偼尵偭偰傕丄懡暘徹柧偼憡摉擄偟偄偲巚偄傑偡丅Galois棟榑偼傕偪傠傫偱偡
偑丄偐側傝崅搙側悢榑偑偄傞傛偆偱偡丅僋儘僱僢僇乕偺掕棟偼丄椺偊偽丄娾攇島嵗婎慴悢妛
悢榑嘦 p274偵偁傝傑偡丅
丂俀師奼戝偺応崌偼丄偄傢備傞丄僈僂僗偺榓(嬻廙偝傫偺A-B丄偨偩偟A=儼pk 偺倫偼丄1偺尨
巒倫忔崻偺娫堘偄偱偟傚偆)傪峫偊傞偺偑晛捠偺傛偆偱偡丅嬻廙偝傫偺傗傜傟偰傞偺偲摨偠偱
偡丅
丂俁師埲忋偼憡摉擄偟偄偲巚偄傑偡丅俁師偺弰夞奼戝偵偮偄偰丄師偺偙偲偑惉傝棫偮傜偟偄
偱偡丅(懡暘偙偺栤戣偺夝寛偵偼栶棫偨側偄偱偟傚偆偑丏丏丏丅)
丂倎丄倐 偼桳棟悢偱丄f(倶)=倶3-3(倎2+ab+倐2)倶-倎3倐3 偼婛栺偱偁傞偲偡傞丅偙偺偲偒丄f(倶)=0 偺
嵟彫暘夝懱偼丄桳棟悢懱忋俁師偺弰夞奼戝偱偁傞丅懄偪丄f(倶)=0 偺弰夞娭悢偑懚嵼偡傞丅
丂倫丄倯偑桳棟悢偱丄f(倶)=倶3+倫倶+倯 偲偡傞丅f(倶)=0 偺嵟彫暘夝懱偑俁師偺弰夞奼戝側傜偽丄
懄偪丄f(倶)=0 偺弰夞娭悢偑懚嵼偡傞側傜丄桳棟悢 倎丄倐 偑懚嵼偟偰丄
丂f(倶)=倶3-3(倎2+ab+倐2)倶-倎3倐3
偲偐偗傞丅
丂俁師偺応崌丄弰夞娭悢偑懚嵼偡傞偨傔偺昁梫廫暘忦審偼丄敾暿幃偑桳棟悢偺暯曽偱偁
傞偙偲偱偡(婛栺惈偼壖掕偟偰)丅偙傟傪巊偊偽慜敿偼偱偒傑偟偨丅屻敿偑傢偐傝傑偣傫丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俀寧係擔晅偗乯
丂偁傝偑偲偆偛偞偄傑偡丅偦偺傛偆側掕棟偑婛偵偁傞偺偱偟偨偐...丅
丂俁師曽掱幃偑弰夞娭悢 B=f(A)丄C=f(B)丄A=f(C) 傪帩偮偲偟傑偡丅偦偆偡傞偲丄
丂1=(A+B+C)/k丂傪巊偭偰丄A2傪丄A丄B丄C偺慄宍寢崌丅A(A+B+C)=kA側偺偱丄AB+AC偼丄A丄
B丄C偺慄宍寢崌丅AB+BC+CA偼掕悢偱偁傞偐傜丄BC偼丄A丄B丄C偺慄宍寢崌丅
丂弞娐揑偵峫偊偰丄CA丄AB傕摨條偱偁傝丄寢嬊丄
丂AA=pA+qB+rC丂丄AB=倶A+倷B+倸C丂丄AC=倷A+倸B+倶C
偲彂偗傑偡丅BB丄BC丄BA摍傕弞娐揑偵摨條偵彂偗傞偼偢偱偡丅
丂A(A+B+C)=kA丂偵傛偭偰丄 p+倶+倷=k丂丄q+倷+倸=0丂丄r+倸+倶=0
丂傑偨丄壜姺丗AB-BA=0丂偺忦審傪寁嶼偟偰尒傞偲丄倸2-倷倸-倶倸+倠倸+倷2-倶倷+倶2=0 偲側傞偺偱丄
倸亗0丂偐偮丂倠=-(倸2-倷倸-倶倸+倷2-倶倷+倶2)/z 偲k偑婯掕偝傟傑偡丅
丂AB+BC+CA=(x+y+z)(A+B+C)丄 ABC=(倶倷-倸2)(A+B+C)丂傪摼傑偡偺偱丄A丄B丄C 偼丄
丂 X3-kX2+(x+y+z)kX+(倸2-倶倷)k=0 偺夝偲彂偗傑偡丅偙偺帪丄
丂AA=(k-倶-倷)A+(-倷-倸)B+(-倶-倸)C丂偲丂k=A+B+C丂偐傜丄B丄C傪徚嫀偡傟偽丄
丂丂B(A)=(AA-(k-倷+倸)A+(倶+倸)k)/(倶-倷)丂丄C(A)=(AA-(k-倶+倸)A+(倷+倸)k)/(倷-倶)
側傫偩偐榖偑弞娐偟偰偟傑偄傑偟偨丅傑偲傔傑偡偲丄
丂弰夞娭悢傪帩偮俁師曽掱幃偺夝偼丄揔摉側倶丄倷丄倸(倸亗0)偵傛偭偰丄
丂丂AA=(k-倶-倷)A+(-倷-倸)B+(-倶-倸)C
丂丂AB=倶A+倷B+倸C
丂丂AC=倷A+倸B+倶C丂where 倠=-(倸2-倷倸-倶倸+倷2-倶倷+倶2)/z
傪枮偨偡昁梫偑偁傝丄媡偵丄偙傟払媦傃A仺B仺C偲弞娐偟偰摼傜傟傞幃払傪枮偨偡A丄B丄C
偼丄忋偵彂偄偨傛偆側弰夞娭悢傪帩偮俁師曽掱幃偺夝偲側傝傑偡丅
(傕偪傠傫偙傟偲墌暘懱偺娭學偑婥偵側傞偺偱偡..)
丂愊偑偱偒傞慄宍嬻娫偲偄偆榖戣偼丄偦傟帺懱偱偪傚偭偲柺敀偄偲巚偄傑偡丅崱夞偱偺儀僋僩
儖(a丆b丆c)=aA+bB+cC偼丄埲壓偺峴楍偲懳墳晅偗傜傟傑偡丅
丂丂ka+倶(b-a)+倷(c-a)丂丄倶(a-b)+倸(c-b)丂丂丄倷(a-c)+倸(b-c)
丂丂倷(b-a)+倸(c-a)丂丂丄kb+倶(c-b)+倷(a-b)丂丄倶(b-c)+倷(a-c)
丂丂倸(b-a)+倶(c-a)丂丂丂丄 倸(a-b)+倷(c-b)丂丂丄kc+倶(a-c)+倷(b-c)
丂偙傟偵傛傝丄儀僋僩儖偺愊傪峴楍愊偲偟偰埖偊傑偡丅奺峴傪崌寁偟偰k偱妱傟偽丄儀僋僩儖偵
暅尦偱偒傑偡丅崱夞偺峫嶡偱偼丄n=3偑摿偵岠偄偰偄側偄傛偆偵尒偊傞偺偱丄堦斒揑側n偵
懳偟偰傕偁傞掱搙摨條偵側傝偦偆偵巚偄傑偡丅
丂丂埲壓丄岺帠拞