完全数 
ある数の約数(但し、自分自身は除く)の総和がある数自身に等しいとき、その数のこと
を、完全数という。
完全数で一番有名な数は、6 である。
実際に、6 の約数は、1、2、3 なので、1+2+3=6 が成り立っている。
6 という数は、神(1)・男(2)・女(3)を含む「世界」を表現しているので、完全数と呼ばれ
たらしい。
kuiperbelt さんからのコメントです。(令和6年12月23日付け)
完全数6についてですが、古代ギリシアでは、数は、2から始まるとされていて、最初の偶数
である2が女性を、最初の奇数である3が男性を象徴していたそうです。
そして、2と3の和である5が結婚を、2と3の積である6が恋愛を象徴していたそうです。
完全数は、6 以外に、28、496、8128、33550336、...などが知られている。
ytk さんからのコメントです。(平成27年3月15日付け)
全然関係ないですが、ISO(国際標準化機構)の規格の一つに「性別コード」(ISO 5218)と
いうものがあって、
0 = not known(不明)、1 = male(男性)、2 = female(女性)、9 = not applicable(該当なし)
という国際基準。「該当なし」を入れているあたり、性的少数者にも配慮できていて好ましい
のかなと。ところで、婚約数は現在発見されている限りではすべて奇数と偶数なのですが、
どちらが男女でどちらが女性というのは決まっているのだろうか?
(追記) Webサイト「数の不思議世界」、平成25年9月19日付けの飯高 茂先生の書き
込みに興味を持った。サイトの読者からの情報とのことです。
約数の和を σ と書くとき、σ(a)=2a が完全数の定義ですが、σ(a)=2a−1 を概完
全数といい、これは2のべきだけだろうという予想があるそうです。
また、σ(a)=2a+1 を擬完全数といい、これの存在は知られていないそうです。
例 a=2n の約数は、 1、2、22、23、・・・、2n なので、
σ(a)=1+2+22+23+・・・+2n=2n+1−1=2・2n−1=2a−1
よって、a=2n は、概完全数であると言える。
さて、完全数を求める面白い方法があることを最近知ったので、ここで、まとめておきたい。
1ばかり並べた2進数を、メルセンヌ数という。
11、111、1111、11111、111111、1111111、...
これらを、十進数に直せば、次のようである。
11=1・2+1=3=22−1
111=1・22+1・2+1=7=23−1
1111=1・23+1・22+1・2+1=15=24−1
11111=1・24+1・23+1・22+1・2+1=31=25−1
111111=1・25+1・24+1・23+1・22+1・2+1=63=26−1
1111111=1・26+1・25+1・24+1・23+1・22+1・2+1=127=27−1
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
メルセンヌ数は、一般に、Mn=2n−1 の形で知られている。
見て分かるように、メルセンヌ数には素数であるものと、そうでないものが混在している。
n が合成数のとき、明らかに、Mn は素数になりえない。Mn が素数となるためには、n
が素数であることが必要条件である。
(追記) 令和5年5月17日付け
上記の「Mn が素数 ならば、n は素数である」ことを示せという問題が、
一橋大学後期(2020)で出題された。有名問題であるが、丁寧な導入もあり、取り組みやす
いだろう。
第1問 a、bを正の整数とする。
(1) a が b の倍数ならば、2a−1は、2b−1の倍数であることを示せ。
(2) 2a−1 が素数ならば、a は素数であることを示せ。
(3) 2a−1=(2a+1)(8a+1) を満たす a を求めよ.
(解)(1) 題意より、a=bk (kは自然数) とおける。このとき、
2a−1=(2b)k−1=(2b−1)((2b)k-1+(2b)k-2+・・・+1)
と書けるので、2a−1は、2b−1の倍数である。
(2) 証明は背理法による。a は素数でないと仮定すると、a=1 または a は合成数
a=1 のとき、 2a−1=1 は素数でない。これは、2a−1 が素数であることに矛盾
a が合成数とすると、a=bk (b、kは2以上の自然数) と書ける。このとき、(1)より
2a−1は、2b−1(≧3)の倍数となり、2a−1>2b−1 より、
2a−1 が素数であることに矛盾
以上から、何れにしても矛盾が導かれるので、a は素数でないと仮定したことが誤りである。
したがって、 2a−1 が素数ならば、a は素数である。
(3) 2a−1=(2a+1)(8a+1)=16a2+10a+1 より、 2a-1=8a2+5a+1
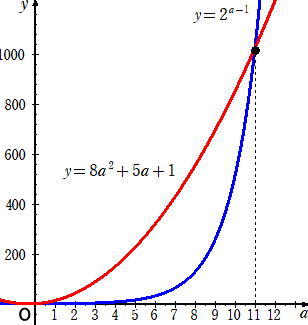
グラフより、a=11のとき、2a-1=8a2+5a+1 を満たす。
実際に、 2a-1=210=1024 、8a2+5a+1=968+55+1=1024 から
成り立つ。 (終)
特に、メルセンヌ数が素数となる場合、それは、メルセンヌ素数といわれる。
(メルセンヌ素数を、単に、メルセンヌ数という場合もある。)
メルセンヌ素数は、まだそれほど数多く(31個位?)は知られていない。
その数が素数かどうかを判定することは、一般に大変であるが、Lucasは、次の非常に
能率的なLucasの定理(ルカステスト)を発見し、その労力は大幅に緩和された。
Lucasの定理(1876年)
数列{an}を、a1=4、an+1=an2−2 により定義する。
4,14,194,37634,1416317954,・・・
このとき、Mn (n は3以上の素数)が素数であるための必要十分条件は、
an−1 がMn で割り切れることである。
例 a2÷M3=14÷7=2 で割り切れる。よって、M3 はメルセンヌ素数である。
a4÷M5=37634÷31=1214 で割り切れる。
よって、M5 はメルセンヌ素数である。
上の例では、実際に、a2、M3 などの値を求めて、割り算を実行したが、その方法は、あ
まり実戦的ではない。次のように計算するのが普通らしい。
M5=31 に注意して、
a1=4 、a2=16−2=14 、a3=142−2=196−2=194≡8 (mod 31)
a4≡64−2=62≡0 (mod 31)
よって、a4 が、M5 で割り切れるので、Lucasの定理より、M5 はメルセンヌ素数である。
メルセンヌ素数を用いると、完全数は簡単に作られる。
定理(Euclid) Mn をメルセンヌ素数とすれば、Mn(Mn+1)/2 は完全数である。
(証明) Mn=2n−1 より、
Mn(Mn+1)/2=(2n−1)・2n/2=(2n−1)・2n−1 である。
この約数の総和は、2n−1 が素数であることに注意して、
(1+2+22+・・・+2n−1)(1+2n−1)=(2n−1)・2n
ここで、 S=1+2+・・・・・・+2n-1 とおくと、2S= 2+22+・・・+2n-1+2n より、
S=2n−1 である。(詳しくは、「約数の個数と和」を参照)
この和から、自分自身を差し引けば、
(2n−1)・2n−(2n−1)・2n−1=(2n−1)・2n−1・(2−1)=(2n−1)・2n−1
となって、自分自身と一致する。
したがって、Mn(Mn+1)/2 は、完全数である。(証終)
(注)この事実は、既にユークリッド原論で示されていることらしい。ギリシャ時代に完全数
は 6、28、496、8128 の4個が知られていたようだ。
例 冒頭であげた完全数は、次のようにして求められる。
M2=3 より、3・(3+1)/2=6
M3=7 より、7・(7+1)/2=28
M5=31 より、31・(31+1)/2=496
したがって、496の次の完全数も容易に求められる。
M7=127 より、127・(127+1)/2=8128
Euler によれば、偶数の完全数は必ずこの方法で求められるようだ。
ところで、奇数の完全数が存在するかどうかは、まだ分かっていないようだ。
(参考文献:小島寛之 著 数学の遺伝子(日本実業出版社)
和田秀男 著 数の世界 整数論への道(岩波書店)
M.ラインズ 著 片山孝次 訳 数 その意外な表情(岩波書店))
(追記) 広島工業大学の大川研究室から情報をいただいた。
2002年6月9日現在、39個のメルセンヌ素数が発見されている。従って、完全数も39個
あることになる。
最大のメルセンヌ素数は、現在、213466917−1で、4,053,496桁の数である。
これらは、スーパーパソコンを用いて計算したのではなく、世界中の20万台以上のパソコ
ンが参加して発見されたとのことである。「すごい!」の一語である。
(追記) 2003年12月3日、過去最大の素数が発見された(検証により、確認)。
220996011−1 632万430桁の数で、40番目のメルセンヌ数だという。
ミシガン州立大学の大学院生マイケル・シェイファー(Michael Shafer)さんが中心となっ
て、世界中の200万台を越えるパソコンを結んで、2年がかりの計算で発見されたとのこと
である。
(追記) 2004年5月15日、過去最大の素数が発見された(検証により、確認)。
224036583−1 723万5733桁の数で、41番目のメルセンヌ数だという。
(追記) 2005年2月27日、過去最大の素数が発見された(検証により、確認)。
225964951−1 781万6230桁の数で、42番目のメルセンヌ数だという。
(追記) 2005年12月15日、過去最大の素数が発見された(検証により、確認)。
230402457−1 915万2052桁の数で、43番目のメルセンヌ数なのかな?
(追記) 2006年9月4日、過去最大の素数が発見された(検証により、確認)。
232582657−1 980万8358桁の数で、44番目のメルセンヌ数なのかな?
(追記) 2008年8月23日、過去最大の素数が発見された(検証により、確認)。
243112609−1 1297万8189桁の数で、47番目のメルセンヌ数なのかな?
発見者は、Edson Smith
(追記) 2008年9月6日、過去最大の素数が発見された(検証により、確認)。
237156667−1 1118万5272桁の数で、45番目のメルセンヌ数なのかな?
(追記) 2009年4月12日、過去最大の素数が発見された(検証により、確認)。
242643801−1 1283万7064桁の数で、46番目のメルセンヌ数なのかな?
発見者は、Odd M.Strindmo
(追記) 2013年1月25日、過去最大の素数が発見された(検証により、確認)。
257885161−1 1742万5170桁の数だという。48番目のメルセンヌ数なのかな?
米国・セントラルミズーリ大学の研究者が見つけたと、世界各地のボランティアのコンピュ
ータをつないで素数探しをするプロジェクト、GIMPSが発表した。
(2013年2月7日付け朝日新聞夕刊)
(追記) 2016年1月21日、過去最大の素数が発見された(検証により、確認)。
274207281−1 (3003764180・・・・・・・1086436351)
2233万8618桁の数だという。49番目のメルセンヌ数なのかな?
A4判の紙にびっしり印刷しても約1万枚必要とのことで、その膨大な量に圧倒される。
米国・セントラルミズーリ大学は、過去最大の素数をクーパー教授が見つけたと、1月21
日、発表した。クーパー教授は、世界各地のボランティアのコンピュータをつないで素数探し
をするプロジェクト「GIMPS」のメンバー。
2015年9月17日にコンピュータは新たな素数を見つけていたが、発見に気付いたのは、
2016年1月7日であったという。(2016年1月24日付け朝日新聞夕刊)
(追記) 2017年12月26日、過去最大の素数が発見されたようだ。
277232917−1 十進法では、2324万9425 桁の数だという。
発見者は、Jon Pace
(追記) 2018年12月、過去最大の素数が発見されたようだ。
282589933−1 十進法では、2486万2048 桁の数だという。
(追記) 2024年10月12日、過去最大の素数が発見されたようだ。
2136279841−1 十進法では、4102万4320 桁の数だという。
発見者は、ルーク・デュラント(米)
881694327・・・486871551
1頁に2500桁詰め込んでも、全部印刷するのに1万6千枚を超えるという。
メルセンヌ素数についての最新情報
(追記) 平成19年12月20日付け
メルセンヌ数
Mn の n の部分を一覧にすると、下記のようになる。
(参考:「メルセンヌ素数について」)
| 1 |
|
2 |
|
3 |
|
4 |
|
5 |
| 2 |
|
3 |
|
5 |
|
7 |
|
13 |
| |
|
|
|
|
|
|
|
|
| 6 |
|
7 |
|
8 |
|
9 |
|
10 |
| 17 |
|
19 |
|
31 |
|
61 |
|
89 |
| |
|
|
|
|
|
|
|
|
| 11 |
|
12 |
|
13 |
|
14 |
|
15 |
| 107 |
|
127 |
|
521 |
|
607 |
|
1279 |
| |
|
|
|
|
|
|
|
|
| 16 |
|
17 |
|
18 |
|
19 |
|
20 |
| 2203 |
|
2281 |
|
3217 |
|
4253 |
|
4423 |
| |
|
|
|
|
|
|
|
|
| 21 |
|
22 |
|
23 |
|
24 |
|
25 |
| 9689 |
|
9941 |
|
11213 |
|
19937 |
|
21701 |
| |
|
|
|
|
|
|
|
|
| 26 |
|
27 |
|
28 |
|
29 |
|
30 |
| 23209 |
|
44497 |
|
86243 |
|
110503 |
|
132049 |
| |
|
|
|
|
|
|
|
|
| 31 |
|
32 |
|
33 |
|
34 |
|
35 |
| 216091 |
|
756839 |
|
859433 |
|
1257787 |
|
1398269 |
| |
|
|
|
|
|
|
|
|
| 36 |
|
37 |
|
38 |
|
39 |
|
40 |
| 2976221 |
|
3021377 |
|
6972593 |
|
13466917 |
|
20996011 |
| |
|
|
|
|
|
|
|
|
| 41 |
|
42 |
|
43 |
|
44 |
|
45 |
| 24036583 |
|
25964951 |
|
30402457 |
|
32582657 |
|
37156667 |
|
|
|
|
|
|
|
|
|
| 46 |
|
47 |
|
48 |
|
49 |
|
50 |
| 42643801 |
|
43112609 |
|
57885161 |
|
74207281 |
|
77232917 |
|
|
|
|
|
|
|
|
|
| 51 |
|
52 |
|
|
|
|
|
|
| 82589933 |
|
136279841 |
|
|
|
|
|
|
?のものは、まだ何番目かが確定していないらしい。(発見者は上記HPを参照)
41番目のメルセンヌ数は、2004年に発見された。723万5783桁と聞いても、あまり
ピンとこないが、1桁当たり4mmの文字の幅(今、この文章を書いている文字の幅!)と
して、1直線にすべて書き並べると、その長さは、
7235783×4÷10÷100÷1000=28.943132 (km)
から、およそ 29 km ほどにもなる。
この距離は、東京都中央区日本橋から第一京浜国道に沿って、ちょうど横浜市神奈川
区までにほぼ等しい。(大体の長さの感覚が掴めたかな?)
(コメント) 1km3分の人が走っても、1時間27分もかかる(!)し、普通に歩いて(分速
80m)も6時間くらいかかる距離ですね。非常に長い数の並びということがイメ
ージできます。
(追記) 平成21年5月9日付け
ゴールデンウィーク中、あまり晴天に恵まれなかったが、今日は久しぶりの好天が望め
そうである。当HPがいつもお世話になっているHN「zk43」さんから、次のような事実を
ご教示いただいた。
6以外の完全数は、1から始まる連続する奇数の立方和で表せる
例えば、
28=13+33(=1+27) 、496=13+33+53+73(=1+27+125+343)
8128=13+33+53+73+93+113+133+153
(=1+27+125+343+729+1331+2197+3375)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
(う〜む、なるほど!)
zk43さんによれば、
13+33+53+・・・+(2n−1)3
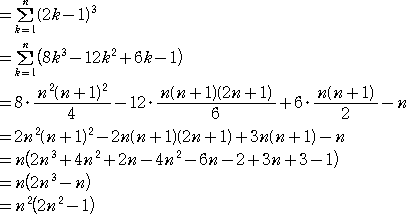
において、 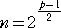 とすると、右辺が 2p-1(2p−1) となり、これは、メルセンヌ数
とすると、右辺が 2p-1(2p−1) となり、これは、メルセンヌ数
Mp=2p−1 に対して、Mp(Mp+1)/2=2p−1(2p−1) が完全数であることから
6以外の偶数の完全数は、必ず、1から始まる連続する奇数の立方和で表せる
ことが示された。
(コメント) 奇数の完全数の存在は、まだ不明だが、奇数の完全数についてはどうなんで
しょうかね?
8128 の次の完全数は、M13=213−1=8191 (1456年 発見者不明)を用いて、
8191×8192÷2=33550336
である。
理論的には明白だが、具体的に確かめてみよう。
33550336=212・8191 なので、約数は全部で、(12+1)(1+1)=26(個)
あり、その約数は、
1、2、4、8、16、32、64、128、256、512、1024、2048、4096、
8191、16382、32764、65528、131056、262112、524224、1048448、
2096896、4193792、8387584、16775168、33550336
で、その総和は、 67100672 で、 67100672÷2=33550336 より、確かに
33550336 は完全数である。
このとき、zk43さんの解法の指針に従えば、n=26=64 なので、
33550336=13+33+53+・・・+1273
と書けることが分かる。
(コメント) とても面白い性質ですね!zk43さんに感謝します。
また、S(H)さんからの情報によれば、偶数の完全数には次の性質もあるそうだ。
偶数の完全数は、三角数である
証明は易しい。
偶数の完全数は、素数 p を用いて、2p−1(2p−1) と表せる(Euler)ので、
2p−1(2p−1)=2p(2p−1)/2=1+2+3+・・・+(2p−1)
より明らかだろう。
さらに、
偶数の完全数の末尾は、必ず、6 または 8 である
という事実も興味深い。
これは、2より大きい素数が、4n+1型か、4n+3型の何れかであることから簡単に示
される。
実際に、 p=4n+1 (n は自然数) のとき、
2p−1(2p−1)=16n(2・16n−1)
ここで、 16n=(10+6)n≡6n≡6 (mod 10) なので、
2p−1(2p−1)=16n(2・16n−1)≡6(2・6−1)≡6 (mod 10)
同様にして、 p=4n+3 (n は自然数) のとき、
2p−1(2p−1)=4・16n(8・16n−1)
ここで、 16n=(10+6)n≡6n≡6 (mod 10) なので、
2p−1(2p−1)=4・16n(8・16n−1)≡4・6(8・6−1)≡4・7≡8 (mod 10)
である。 p=2 のときの完全数は6なので、もちろん命題は成り立っている!
(コメント) S(H)さんの情報検索はスゴイですね!いつも感謝しています。
奇数の完全数の存在は、まだ不明らしいが、奇数の完全数に関して、zk43さんより情報
をいただいた。(平成21年5月13日付け)
素因数の種類が2種類の奇数は完全数ではない
(証明) N=pm・qn (p、q は奇素数で、p<q、m、n は自然数)とする。
このとき、Nの正の約数の総和 S は、
S=(1+p+p2+・・・+pm)(1+q+q2+・・・+qn)
そこで、
S/N=(1/pm+1/pm-1+・・・+1/p+1)(1/qn+1/qn-1+・・・+1/q+1)
<(1+1/p+1/p2+・・・+1/pm+・・・)(1+1/q+1/q2+・・・+1/qn+・・・)
≦(1+1/3+1/32+・・・+1/3m+・・・)(1+1/5+1/52+・・・+1/5n+・・・)
よって、 S/N<{1/(1−1/3)}・{1/(1−1/5)}=15/8<2
もし、Nが完全数ならば、 S=2N でなければならないので、このことから、
素因数の種類が2種類の奇数は完全数にはなり得ない
ことが示された。 (証終)
(コメント) zk43さん、ありがとうございます。奇数の完全数って、本当に存在するのでしょ
うか?
当HPの掲示板「出会いの泉」に、当HPがいつもお世話になっているHN「GAI」さんが、平
成25年1月27日付けで、次のような書き込みをされた。
「2n−1が素数なら、(2n−1)・2n-1は完全数である」というユークリッド時代から知られて
いたことから、2n−1がいつ素数になるかが問われ、nが合成数なら必ず因数分解されてし
まうので、nは素数pについて調べられていった。
メルセンヌは1649年の手紙の中で、
p=2、3、5、7、13、17、19、31、67、127、257 のとき、2n−1が素数(メルセンヌ素数)
であると証明抜きで発表したとある。(もちろん高性能のコンピュータは存在しない。)
現在、これらが素数になれるものがコンピュータの道具も使って、
p=2、3、5、7、13、17、19、31、61、89、107、127、521、607、…、13466917
(→ 参照:「A000043」)
と現在まで39個見つかっているという。従って、メルセンヌは、p=61を見過ごし、67、257を
誤って判断したことになる。
そこで、メルセンヌが間違った p=67について、267−1の因数分解は?に興味が湧いた。
原理的には、「floor(sqrt(2^67-1))=12148001999」より、1〜12148001999 までに現れるす
べての素数でことごとく割っていけば目的が達成できるが、この中の素数は余りにも多すぎ
る。(547932122個もある。)
そこで、コンピュータがない時代にメルセンヌが判断を間違えないようにするためには、こ
の因数分解をどの様に行えばよいかのアイデアを教えて下さい。
当HPがいつもお世話になっているHN「空舟」さんからのコメントです。
(平成25年1月27日付け)
Webサイト「フェルマー素数について」によると、1880年、ランドリーは(82才という高齢にも
かかわらず)、264+1 の素因数分解が
F6=274177×67280421310721
となることを示しました。でもどうやって見つけたのかは書かれていませんでした。こちらを
考察してみました。
264+1≡0 (mod p) とおくと、URLにも有るように、p=128N+1型です。
p=128N+1、q=128M+1、pq=264+1 とおくと、M=(257−N)/(128N+1)
M=(257−N)/(128N+1)が割り切れる必要条件を調べればNを絞れるかもしれないと思っ
たのですが、なかなか考察が進めないです。[実際の答えは、N=4284、M=525628291490]
同様に、267−1=(67N+1)(67M+1) とおくと、式 M=(A−N)/(67N+1) を得ます。
(ここで A=2・(266−1)/67=2202596307308603178)
ここで、M、Nは明らかに偶数なので、M=2m、N=2n、A=2a とおいても良いですね。
m=(a−n)/(134n+1) 、a=(266−1)/67=1101298153654301589
[実際の答えは、 n=1445580、 m=5685360129]
GAI さんからのコメントです。(平成25年1月27日付け)
上記のアイデア(フェルマーの小定理の活用?)から探すべき素数は、p=134k+1型
に限って調べればよい。(だいぶ絞れることにはなるが・・・)
そこで、PARIという計算ソフトでこっそり調査してみました。
?
for(k=1,1450000,if(isprime(134*k+1)==1,if(component(Mod(2^67-1,134*k+1),2)==0,print(k,";",134*k+1))))
で実行したら、「1445580 、193707721」の結果がヒットしました。これから、
267−1=193707721×761838257287
と分解でき、合成数であることが確認できました。しかし、これを当時手計算で達成できるも
のだろうか?不思議はさらに深まりました。
(追記) GAI さんが、メルセンヌ数の歴史を調べられた。(平成27年3月14日付け)
pを奇素数とするとき、M(p)=2p−1 (メルセンヌ数)が素数になるのか?まあ、
p=3 --> M(3)=2^3-1=7
:prime
p=5 --> M(5)=2^5-1=31 :prime
p=7 --> M(7)=2^7-1=127
:prime
p=11 --> M(11)=2^11-1=2047
?(実は23*89に分解可能)
p=13 --> M(13)=2^13-1=8189
?
p=17 --> M(17)=2^17-1=131071 ?
p=19 --> M(19)=2^19-1=524287 ?
・・・・・・
p=67 --> M(67)=2^67-1=147573952589676412927
・・・・・・
p=127 --> M(127)=2^127-1=170141183460469231731687303715884105727
・・・・・・
p=257 --> M(257)=2^257-1
=231584178474632390847141970017375815706539969331281128078915168015826259279871
これに対し、メルセンヌは、1644年に、
p=2、3、5、7、13、19、31、67、127、257 だけが素数になる
と予想した。
(この予想は誰もこんな大きな数では確認出来ないだろうと高をくくったある意味ハッタリ)
<後日p=67は間違いで、また、61、89、107 が抜け落ちていることが判明する。>
しかし、この予想に果敢にも挑戦した人が現れ、1876年エドアール・リュカが19年の歳月
をかけて、M(127)が素数であることを確認したという。
その方法は、pが、p≡3 (mod 4) である素数のとき、
S(0)=3、S(n)=S(n-1)2-2 (n=1、2、3、・・・)
と定義するとき、S(p-2)がM(p)で割り切れれば、M(p)は素数であるというものである。
実際、p=7、11 で確認してみると、
S(0)=3 、S(1)=S(0)^2-2=3^2-2=7 、S(2)=S(1)^2-2=7^2-2=47 、S(3)=S(2)^2-2=47^2-2=2207
S(4)=S(3)^2-2=2207^2-2=4870847 、S(5)=S(4)^2-2=4870847^2-2=23725150497407
S(6)=23725150497407^2-2=562882766124611619513723647
S(7)=562882766124611619513723647^2-2=316837008400094222150776738483768236006420971486980607
以下
S(8)=1003856898919213766887542399928262567048796276831819015150993986
13465618884806971304035121947368905594088447
S(9)=1007728673507700566098200806106507306807447530046601244462938848757476965211565176350
00261283676793017447903659202787756017660002174559979308093950457876685360362550516268
2177708433023235042368022152858871807
これらの数に対し、
S(5)/M(7)=23725150497407/127=186812208641(ピタリ割り切れる)
しかし、S(9)/M(11)の計算は余りが1034となり割り切らない。つまり、M(7)=127は素数で、
M(11)=2047は合成数であると主張する。
この原則に則って、リュカは19年という歳月をかけて、M(127)の素数性を示した。
(手計算で素数を確認された最大の記録であることは未だに破られていない。)
この判定を用いると、実は、M(67)も合成数であることが判るという。しかし、どのような分
解になるのかはリュカの方法では出てこない。
これに対し、1903年コロンビア大学数学教授フランク・ネルソン・コールが夕食後の一時
を3年計算し続けて、M(67)=193707721*761838257287 を見つけたという。
数学者の素質として本当に粘り強い気質、倦まず弛まず歩き続ける忍耐力が必要な条件
であることをしみじみ教えてくれます。素数で片端から割っていくという方法からリュカのある
意味単純作業の繰り返しによる素数判定という新たな道が開けたことの意味は大きい。しか
し、それでも莫大な数字に膨れていくことは難点でもある。
これに対し、1930年デリック・ヘンリー・レーマーがリュカの方法に画期的な改良を加え、
M(257)が合成数であることを証明する。(この経緯は次回に...)
GAI さんからの続報です。(平成27年3月15日付け)
さて、リュカによる素数判定テストを受けて、デリック・ヘンリー・レーマーは(この人の父は
20世紀の初めには10017000までの素数表を作成したという。)、子供心に父の背中を見て
育ったんでしょう、彼が25歳の時リュカの素数判定を劇的に効率化させる方法を編み出した。
それが、数列S(n)を、 S(1)=4、S(n+1)=S(n)-2 (mod M(p)) :M(p)=2^p-1 (p:prime)
で定義しておけば、 S(p-1)≡0 (mod M(p)) ⇔ M(p)は素数
ここに、modの世界で処理するところに画期的な進歩をもたらす。
(確かめ) M(7)=2^7-1=127 は素数、M(11)=2^11-1=2047は合成数、M(13)=2^13-1=8191は
素数を見てみる。
S(1)=4 (mod 127)
S(2)=S(1)^2-2=4^2-2=14 (mod 127)
S(3)=S(2)^2-2=14^2-2=194≡67 (mod 127)
S(4)=S(3)^2-2=67^2-2=4487≡42 (mod 127)
S(5)=S(4)^2-2=42^2-2=1762≡111 (mod 127)
S(6)=S(5)^2-2=111^2-2=12319≡0
(mod 127) ・・・ 従って、M(7)は素数
S(1)=4 (mod 2047)
S(2)=S(1)^2-2=4^2-2=14 (mod 2047)
S(3)=S(2)^2-2=14^2-2=194 (mod 2047)
S(4)=S(3)^2-2=194^2-2=37634≡788 (mod 2047)
S(5)=S(4)^2-2=788^2-2=620942≡701 (mod 2047)
S(6)=S(5)^2-2=701^2-2=491399≡119 (mod 2047)
S(7)=S(6)^2-2=119^2-2=14159≡1877 (mod 2047)
S(8)=S(7)^2-2=1877^2-2=3523127≡240 (mod 2047)
S(9)=S(8)^2-2=240^2-2=57598≡282 (mod 2047)
S(10)=S(9)^2-2=282^2-2=79522≡1736 (mod 2047)
もし、S(10)≡0 (mod 2047)であったなら、M(11)は素数であったのに、ここではそうではない
のだから、M(11)=2047(=23*89)は合成数
S(1)=4 (mod 8191)
S(2)=S(1)^2-2=4^2-2=14 (mod 8191)
S(3)=S(2)^2-2=14^2-2=194 (mod 8191)
S(4)=S(3)^2-2=194^2-2=37634≡4870 (mod 8191)
S(5)=S(4)^2-2=4870^2-2=23716898≡3953 (mod 8191)
S(6)=S(5)^2-2=3953^2-2=15626207≡5970 (mod 8191)
S(7)=S(6)^2-2=5970^2-2=35640898≡1857 (mod 8191)
S(8)=S(7)^2-2=1857^2-2=3448447≡36 (mod 8191)
S(9)=S(8)^2-2=36^2-2=1294 (mod 8191)
S(10)=S(9)^2-2=1294^2-2=1674434≡3470 (mod 8191)
S(11)=S(10)^2-2=3470^2-2=12040898≡128 (mod 8191)
S(12)=S(11)-2=128^2-2=16382≡0
(mod 8191) ・・・ 従って、M(13)は素数
狐に抓まれる様に感じるが、確かに合っている。リュカの判定法が数が膨大なものに膨れ
上がって行くのに対し、レーマーの方法はmod計算内の数値で事済む。
ふと、どのような経緯でこの法則を発見したものか?という疑問が湧く。
(ネットではこの判定法の証明とやらが書かれてあるが、これはあくまで論理的に後証明した
ものと思われる。)
子供の頃から父親が熱心に取り組んでいる姿をみて、小さい子供ながら素数には人一倍
強い関心を持ち、自らもお手伝いの意味も含んで、素数を用いたたくさんの計算を経験して
いて、その中から素数に対する感覚が研ぎ澄まされていき、既にリュカによる漸化式的判定
方法をまねて作業する中で、ある日突然上記の法則に気づいてしまった、という私の勝手な
空想が広がっていくのでした。
もうこの世にはいないヘンリー・レーマーにインタヴューするわけにはいかず、真相は闇の
中ですが、論理的に攻めたというより経験則から確信に至る経緯を通して、このテストはこ
の世に生まれ出たと思います。
(こんな法則が潜んでいたことをよくも発見したものだと感心します。)
したがって、それまで誰も辿り着けなかった
M(257)=2^257-1=231584178474632390847141970017375815706539969331281128078915168015826259279871
なる想像を絶する数に対しても、
S(256)≠0 (mod 231584178474632390847141970017375815706539969331281128078915168015826259279871)
の確認よりM(257)は合成数である(即ちメルセンヌの予想は外れた。)と結論できた。
実際、
231584178474632390847141970017375815706539969331281128078915168015826259279871
=535006138814359*1155685395246619182673033*374550598501810936581776630096313181393
これが、1930年というからメルセンヌの予想(1644年)から286年後のことである。リュカの
発想とガウスのmod的世界観が混ざり合い、それが火花を発してレーマーテストが生まれ出
たと思える。
(追記) 「古の人の足跡を辿って」と題して、GAI さんからの投稿です。
(平成29年10月20日付け)
メルセンヌ素数(M(p)=2p-1(pは素数))を見つけ出す方法に、リュカとレーマーのテスト方
法があり、リュカテストでは、
素数pが 4*j+3 型であれば、S[0]=3、S[n]=S[n-1]2-2 (n≧1) の漸化式とするとき、
初めて S[p-2]≡0 (mod M(p)) が成立すれば、M(p)=2p-1 は素数である。
(実例) p=7 は、4*j+3 型の素数で、メルセンヌ数が、M(7)=27-1=128-1=127
S[0]=3 、S[1]=S[0]^2-2=3^2-2=7 、S[2]=S[1]^2-2=7^2-2=47 、
S[3]=S[2]^2-2=47^2-2=2207≡48 (mod 127) 、S[4]=S[3]^2-2=48^2-2=2302≡16 (mod
127)
S[5]=S[4]^2-2=16^2-2=254≡0 (mod 127)
よって、S{5]≡0 (mod M(7)) のテストを受け、M(7)=27-1(=127) が素数と判定。
この道具を使うことにより、メルセンヌが素数になるであろうと予想していた
M(127)=2127-1 (39桁の莫大な数)
も、この作業を地道に続けていけば可能となる。事実リュカは1876年(19年間も計算を続けて
の結果と読んだことがある。)M(127)が素数であることを確認したという。
(コンピュータではほんの数秒で確認可能)
ところがメルセンヌが次に予想しているM(257)は、257が 4*j+1 型素数であるため、この方
法では確認できない。
これに対し、レーマーがリュカの方法を改良し、リュカのテスト発表から約半世紀後、1930年
何とほんの僅かの差だが、
どんな奇素数pでも、 S[0]=4、S[n]=S[n-1]2-2 (n≧1) の漸化式とするとき、
初めて S[p-2]≡0 (mod M(p)) が成立すれば、M(p)=2p-1 は素数である。
を公表し、リュカテストでは判定不可能だったタイプの素数に対してもチェック出来ることに
なった。こうしてメルセンヌが予想もしていなかったM(61)、M(89)などが素数であることが認
められていく。そして念願のM(257)は遂に1922年素数ではないことで決着がつくという。
なお、M(127)以降のものはM(521)まで進めないと存在しないという。(1952年決着)
このようにリュカとレーマーのテストの違いはほんの初期条件S[0]の値だけである。リュカ
があれだけのテストを編み出す能力があればそこに気が付かなかったのか、また半世紀も
の間、誰も初期設定をS[0]=3からS[0]=4 へを行わなかったのか・・・不思議でなりません。
(コンピュータの確認計算では確かにこの変化は劇的に起こることは感じられますが、なぜ
それが可能なのかは分かりません。)
ちなみにS[0]の値をいろいろ変化させてみると、S[0]=10 ならレーマーテストと同じ判定方
法がとれ、S[0]=14 ならS[p-3]≡0 (mod M(p)) で、M(p):素数の判定がとれそうです。でも、
なぜこれらの初期値でそれが起こるのか霧の中です。
らすかるさんからのコメントです。(平成29年10月20日付け)
S[0]=4、S[n]=S[n-1]2-2 (n≧1) の漸化式とするとき、S[1]=14ですから、M(p):素数の判
定がとれるのは当然ではないでしょうか。
DD++さんからのコメントです。(平成29年10月20日付け)
なるほど、では初期値を変えることを閃いた GAI さんが、ぜひ S[0]=5 や S[0]=6 に変更し
たらどうなるかサクッと発表してください。もちろん、その方法できちんと素数である確認が
できるという証明付きで。
GAIさんからのコメントです。(平成29年10月20日付け)
S[0]=5 のとき、pが 6j-1型の素数なら、S[p-1]=S[p]≡2 (mod M(p))
pが 6j+1型の素数なら、S[p]≡23 (mod M(p))
S[0]=6 のとき、S[p-1]≡6 (mod M(p))
でしょうか。
この証明ができれば夢のような話で、あくまで計算で出てくる結果で予想しているだけで・・・。
あッ!もしかしてS[0]=4でスタートすることで完璧なチェックがなされることを証明することが、
果たして簡単に証明可能なのか?をおっしゃりたい趣旨で言われていることなんですかね?
(でもリュカさんなら出来そうですが・・・;聞いてみないと分からないですかね。)
DD++さんからのコメントです。(平成29年10月20日付け)
はい。元祖リュカテストについてはウェブ検索してもあまり出てこず、朧げな記憶を頼りにし
た話になってしまいますが、たしか証明はフィボナッチ数とリュカ数の関係からだったと思い
ます。つまり、
F[0]=0、F[1]=1、F[n+2]=F[n+1]+F[n] で、0, 1, 1, 2, 3, 5, 8, …… というフィボナッチ数ができ
るのに対し、
L[0]=2、L[1]=1、L[n+2]=L[n+1]+L[n] で、2, 1, 3, 4, 7, 11, 18, …… というリュカ数ができ、
これらの数の間には、 L[n]=F[n+1]+F[n-1] や F[2n]=F[n]L[n] といった密接な関係があり
ます。
(→ 参考:「リュカ≒フィボナッチ≒ピタゴラス」、「リュカ数」)
そして、このリュカ数の 2n (n≧1) 番目だけ採用する、つまり S[n]=L[2n] とすると、
S[1]=3、S[n+1]=S[n]2-2
という数列ができていきます。この S[n] について、F[n] と L[n] の性質を使いながらいろいろ
調べていくと、元祖リュカテストが得られる、という話だったと思います。
(具体的にどうやるのだったかは忘れました)
ということは、S[0]=3 というのは、適当に選んだ初項ではなく、2番目のリュカ数 L[2]=3 に
由来するものなので、S[0]=4 にした話を証明するにはフィボナッチ数やリュカ数を投げ捨て
て最初の一歩から考えないといけません。
リュカはフィボナッチ数やリュカ数を一般化したリュカ数列(リュカ数を並べた数列という意
味ではない)を作ったわけですが、なぜそんな一般化をしようとしたのかと想像してみると…
やっぱり S[0] の一般化をしようとリュカが試行錯誤した形跡なのだろうと私は思うのですが、
いかがでしょう。
GAI さんからのコメントです。(平成29年10月21日付け)
なるほど、S[0]=3 と S[0]=4 とは全く異なる考え方による偶然の一つ違いであったのですか!
以前からフィボナッチ数列の漸化式とリュカ数列での漸化式は初期条件こそ異なるが、まっ
たく同形式の漸化式なのに、なぜわざわざ異なる呼び名を使用しているんだろうと不思議に
感じていました。
さる本で、黄金分割比φ=(1+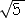 )/2に対して、
)/2に対して、
φn=((1+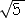 )/2)n=(L[n]+F[n]*
)/2)n=(L[n]+F[n]*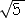 )/2 (n=0,1,2,3,・・・)
)/2 (n=0,1,2,3,・・・)
{L[n]}:2,1,3,4,7,11,18,29,・・・ {F[n]}:0,1,1,2,3,5,8,13,21,・・・
なるリュカ数列とフィボナッチ数列を使うと何かド・モアブルの定理を思わせることが可能なん
だと妙に感じ入ったことがありました。
この数列の利用が、このメルセンヌ素数の決定に深く関わっていたとは知りませんでした。
あるサイトでこのレーマーテストの証明を見ましたけど、何やらガウスの平方剰余の相互法
則などを駆使しながら背理法を用い論理の綱渡りをサーカスよろしく、巧みにわたり切って
いる様を口をあんぐりと開けて眺めていました。いやいや先人の残された遺産は人類の宝
です。